一种基于局部中心性的网络关键节点识别算法
郑文萍 吴志康 杨 贵
1(山西大学计算机与信息技术学院 太原 030006)2(计算智能与中文信息处理教育部重点实验室(山西大学) 太原 030006)3(山西大学大数据科学与产业研究院 太原 030006)
近年来,对各种复杂网络的研究是许多领域关注的热点之一,如生物网络、社交网络、交通网络、引文网络等已成为众多学者的主要研究对象[1-4].研究发现网络机能往往受网络中一小部分节点的影响,这部分节点的功能失效会导致网络性能下降.并且这部分节点的失效影响会快速波及到整个网络,并最终使网络陷入瘫痪.基于此,对网络连通性至关重要的那部分节点被称为关键节点.此外,关键节点识别是分析与理解网络特性、结构以及功能的重要方式[5-6],且在发现药物靶点、发现关键蛋白质、控制传染病的爆发以及快速定位恐怖组织等方面意义重大[7-9].因此如何在大规模网络中快速搜索关键节点,并加强对关键节点的监控和保护,对维持网络性能、确保复杂系统功能可靠性与健壮性十分重要.
本文提出一种基于节点中心性的网络关键节点识别算法框架(greedy algorithm for critical node problem, GCNP): 根据某种中心性指标得到网络的点覆盖集;从网络中删除点覆盖集,并迭代选择点覆盖集中使网络连通的节点对增加最少的节点向原网络回添,直至点覆盖集中节点满足用户给定的待删除关键节点数.为了更好地选择初始的点覆盖集,本文还提出了一种基于局部拓扑结构特征的节点中心性度量(local neighbor centrality, LNC).实验结果表明,采用合理的中心性度量指标选择初始点覆盖集可以有效提高关键节点识别性能,且本文所提的LNC指标能更准确地评估节点的重要性.
1 相关工作
网络关键节点识别问题(critical node problem, CNP)形式化定义为:对于图G=(V,E)和正整数k,确定节点子集S⊆V且|S|=k,使得导出子图G[VS]中连通的节点对最少.确定一个网络的包含k个节点的最优子集S是NP困难问题[10].
节点中心性是刻画节点关键性的重要指标.目前已经提出许多节点重要性度量指标,包括度中心性(degree centrality, DC)[11]、介数中心性(between-ness centrality, BC)[12]、接近中心性(closeness centrality, CC)[13]、PageRank[14]等.其中度中心性是刻画节点重要性最简单的指标,文献[15]表明在无标度网络或指数网络中,只存在小部分大度节点,这些节点具有较高的重要性;然而网络中大多数节点都是小度节点,为了对这些节点重要性进行度量,需要考虑其更广泛的拓扑结构信息.介数中心性[6,12]定义为经过一个节点的最短路径占网络所有最短路径的比值,通常一个节点介数中心性越高,越有可能位于多个社区的“桥接”处,其对保证网络连通性也越重要.接近中心性[13]通过计算节点到网络其他所有节点的最短路径长度来刻画节点到网络中心的趋近程度.通常节点的接近度中心性越高,表明该节点越趋近网络的中心.尽管介数中心性和接近中心性较好地考虑了节点在网络连通性方面的重要性,然而由于需要预先知道网络的全局信息,计算复杂度高,不适用于大型复杂网络.
Chen等人[16]提出了LR中心性(LocalRank),通过考虑节点4阶邻域信息来衡量节点重要性.王建伟等人[17]综合考虑节点自身度与邻居节点的度数和来衡量节点重要性,称为局部度和中心性(local degree sum centrality, LDS).LocalRank中心性仅考虑邻域中节点个数,局部度和中心性只考虑节点的度信息,两者都忽略了邻域中节点间的拓扑结构,无法有效识别网络中关键节点的重要性.任卓明等人[18]综合考虑节点的度数和聚集系数,提出了一种基于邻居信息与聚集系数的节点重要性评价算法.Kitsak等人[19]提出节点重要性取决于其在网络中的位置,并指出经过K壳(K-Shell, KS)分解得到的节点的壳值可以较好地刻画了节点的重要性.目前已经提出一系列扩展和改进的K壳指标[20-22].
Arulselvan等人[10]提出了一种基于贪心策略的关键节点识别算法,首先从网络G=(V,E)中随机选取节点构成网络的一个极大独立集M,从其余节点中选择添加后使导出子图G[M]中连通节点对数增量最小的节点加入M,直到|M|=|V|-k为止.Addis等人[23]提出了一种基于贪心策略的多启动关键节点识别算法,从网络中删除一个随机选择的点覆盖集S(|S|>k);再从S中选择使得网络中连通节点对数增加最小的节点向原网络回添.
基于贪心策略的关键节点识别方法可以在较短时间内得到网络中对连通性影响最大的k个关键节点,适用于大规模网络中的关键节点识别问题.然而,上述基于贪心策略的算法中,随机选择初始节点独立集或覆盖集,结果存在较大的随机性.同时随机选择的初始集合规模与最终目标集合规模相差较大,导致算法需要进行更多的回添节点操作.
采用合理的中心性指标选择初始节点集合,可以有效解决贪心算法结果随机性较大的问题.基于此,本文提出一种基于节点中心性的网络关键节点识别算法框架GCNP:根据某种节点中心性指标选择网络的节点覆盖集S;从网络中删除S,并迭代选择S中使网络连通的节点对增加最少的节点向原网络回添,直到|S|=k为止.为了更好地选择初始的节点覆盖集,本文还提出了一种基于局部拓扑结构特征的节点中心性度量指标LNC.在真实网络数据集和人工网络数据集上的实验结果表明,采用合理的中心性指标选择初始点覆盖集可以有效提高关键节点识别性能.在GCNP算法框架下,将本文所提的LNC指标与度中心性(DC)、LocalRank中心性(LR)、K壳中心性(KS)、局部度和中心性(LDS)相比较,发现LNC指标能更准确地评估节点的重要性.
2 背景知识
定义1.复杂网络.可以用图G=(V,E)来表示,其中节点集V={v1,v2,…,vn},边集E={(vi,vj)| 1≤i,j≤n}代表网络个体间联系的集合.|V|和|E|分别为图G的节点数和边数.节点vi的邻域Г(vi)={vj|(vi,vj)∈E,vj∈V}.Г(vi)中的节点称为节点vi的邻居节点,节点vi的度di=|Г(vi)|.除非特别指明,本文仅考虑简单无向图.
在无向图G中,如果从节点vi到节点vj有路径,则称vi和vj是连通的.如果对于图G中的任意2个节点vi,vj∈V,vi和vj都是连通的,则称图G是连通的.对于一个包含由m个节点的连通图,连通节点对数为m(m-1)2.vi和vj之间的距离就是2个节点之间最短路径的长度.
对图G=(V,E)和G′=(V′,E′),如果V′⊆V且E′⊆E,则称G′是G的子图,记作G′⊆G.若G′是以V′为顶点集,以2个端点均在V′中边的全体为边集,则称G′是G的导出子图,并记为G[V′].
定义2.网络关键节点识别问题[23].对于图G=(V,E)和正整数k,确定包含k个节点的节点子集S⊆V,使得删除子集S后,导出子图G[VS]中的连通节点对最少.
LocalRank中心性[16]利用节点的4阶邻域内所包含的信息刻画节点在全局网络中的重要性,是在权衡效率和性能的基础上对度中心性的扩展.令N(vw)表示图G中与节点vw的距离不超过2的节点集合,定义
(1)
则节点vi的LocalRank中心性定义为
(2)
其中,Г(vi)表示节点vi的邻居节点集合.
3 基于节点中心性的关键节点识别算法
3.1 问题定义
定义3.关键节点问题(CNP).对无向图G=(V,E),确定一个节点子集S⊆V,使得|S|≤k且从G中删除S所得的导出子图G[VS]中连通节点对数f(S)最小.其中
(3)
Ci表示删除集合S后G[VS]中的第i个连通分量,δi是连通分量Ci中的节点数.
3.2 GCNP算法框架
由于确定一个网络的包含k个节点的最优子集S是NP困难问题.为了在合理的时间得到一个较优的大小为k的关键节点集合,本文提出一个基于局部中心性的关键节点识别算法框架 (greedy algorithm for critical node problem, GCNP).
GCNP迭代选择中心性指标最高的节点加入集合S,直至S成为网络的一个点覆盖集,通常|S|>k.迭代地从S中选择使得网络连通节点对增加最小的节点回添至原网络,直到|S|=k.基于节点中心性指标的关键节点识别算法框架GCNP(σ)如算法1所示,其中σ代表某种中心性指标,如度中心性、介数中心性、LocalRank中心性等.
算法1.GCNP(σ)算法框架.
输入:网络G=(V,E)、正整数k、中心性指标σ;
输出:节点子集S⊆V,且|S|=k.
Step1.S=∅,V′=V;
Step2. 计算V′中每个节点的中心性指标值σ(vx);
Step4. 令S=S∪{vi},V′=V′{vi};
Step5. 若G的导出子图G[VS]中存在边,转Step2;
Step6. 根据式(3)计算f(S),若|S|≤k,转Step10;
Step7. 对S中的每个节点计算f(S{vx});
Step9.S=S{vi},若|S|>k,转Step7;
Step10. 输出S.
任何一种节点中心性指标σ都是从不同角度衡量了节点在特定拓扑特征下的关键性.σ值越高,节点越有可能是关键节点.如果将网络节点仅按照某种中心性指标σ值由高到低排序,并选择前k个节点作为关键节点集,可能会遗漏一些σ值不高但对网络连通性比较关键的节点.
为了提高关键节点识别性能,GCNP(σ)算法中按照某种中心性指标σ选择网络的一个初始点覆盖集合S,并按照目标函数选择S中对网络连通性影响最小的节点回添.表1给出了在部分人工网络数据[23]上分别采用σ指标和本文GCNP(σ)算法选择k个关键节点,删除这些节点后原网络的连通点对数,其中σ采用本文第1节给出的度中心性(DC)、LocalRank中心性(LR)、K壳中心性(KS)、局部度和中心性(LDS).从表1可以看出,GCNP(σ)在关键节点识别性能方面有非常大的改进.
网络中节点的中心性与节点度及其邻域拓扑结构密切相关.这使得度中心性不足以准确度量节点在网络连通方面的重要性,LocalRank中心性统计了节点vi的4步邻域中的节点数,并没有考虑其邻域节点间的拓扑结构.K壳中心性通常将网络中节点划分为不同的层次,无法区分同一层次中包含的大量节点的中心性.局部度和中心性没有考虑节点邻域连接的紧密程度对其中心性的影响.
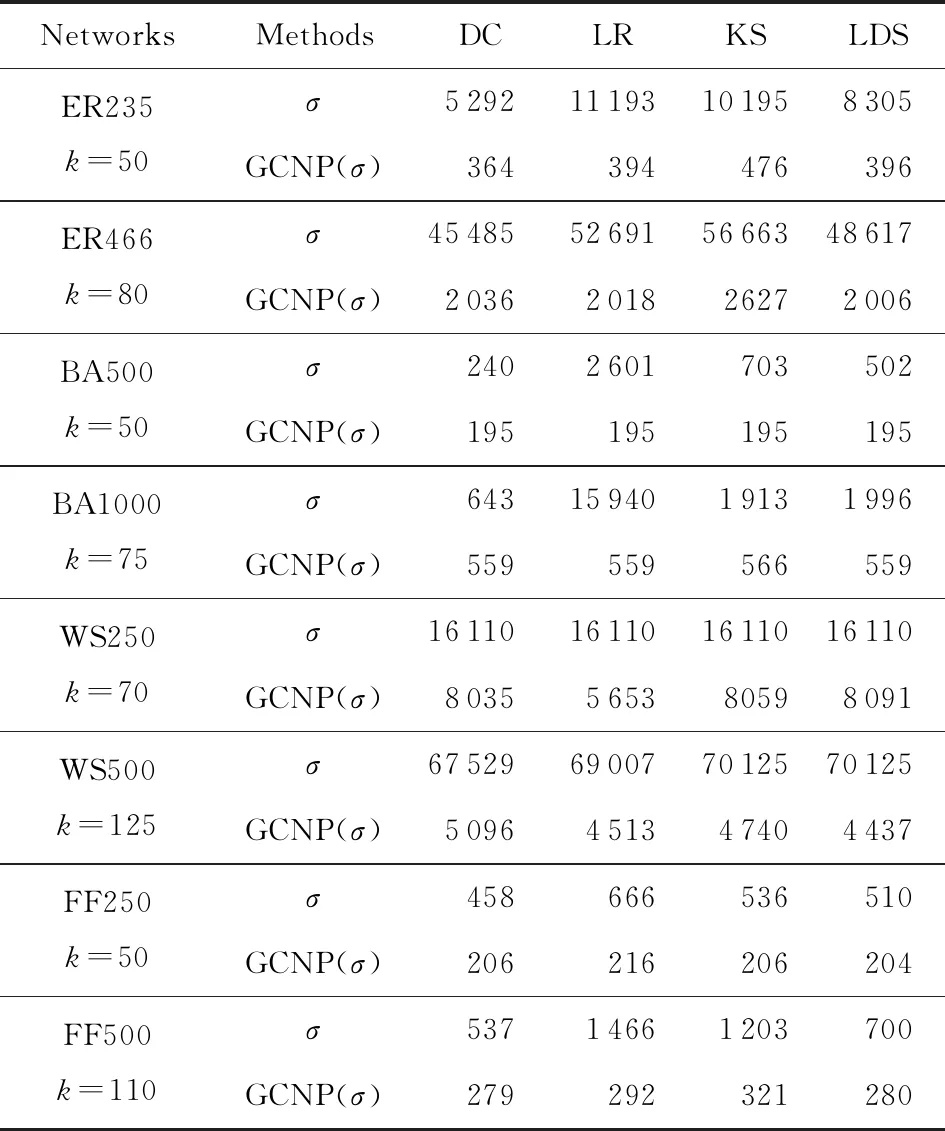
Table 1 Pairwise Connectivity of σ and GCNP(σ) 表1 σ与GCNP(σ)在各指标上的连通节点对数
为了更合理地对网络节点的中心性进行度量,进一步利用节点的度和邻域拓扑结构提出基于节点局部中心性的度量指标LNC.
4 节点的局部中心性(LNC)度量
为了更好地利用节点度和邻域拓扑结构对节点中心性进行度量,本文提出一种节点的局部中心性度量指标LNC,衡量节点对网络连通性的影响.如果一个节点对网络连通性影响越大,则与该节点关联的边通常对局部网络连通性影响越大.因而,可以通过节点所连边对局部网络连通性的影响来反映该节点在网络连通性方面的重要性,节点所连边的重要性越高,该节点往往越重要.基于此,本文首先考虑网络中边权重.对边(vi,vj)∈E而言,节点vi和vj度越大,则该边权重越大;节点vi和vj之间公共邻居节点越少,则边(vi,vj)对vi与vj之间的连通性影响越大,其权重也越大.式(4)给出了边权重的定义.
令vi和vj是网络中的2个节点,其权重wi,j定义为

(4)
其中Г(vi)是节点vi的邻居节点集合,di为节点vi的度数,|Γ(vi)∩Γ(vj)|表示节点vi和节点vj之间的公共邻居节点数.
如图1所示网络[24]中的2条边(v10,v20)和(v19,v17),其中d10=d19=4且d20=d17=3.尽管2条边对应度相同,但由于|Γ(v10)∩Γ(v20)|=0,而|Γ(v19)∩Γ(v17)|=1,且v15的度数较大,因而有w10,20>w19,17,即边(v10,v20)对网络连通性的重要性大于边(v19,v17).
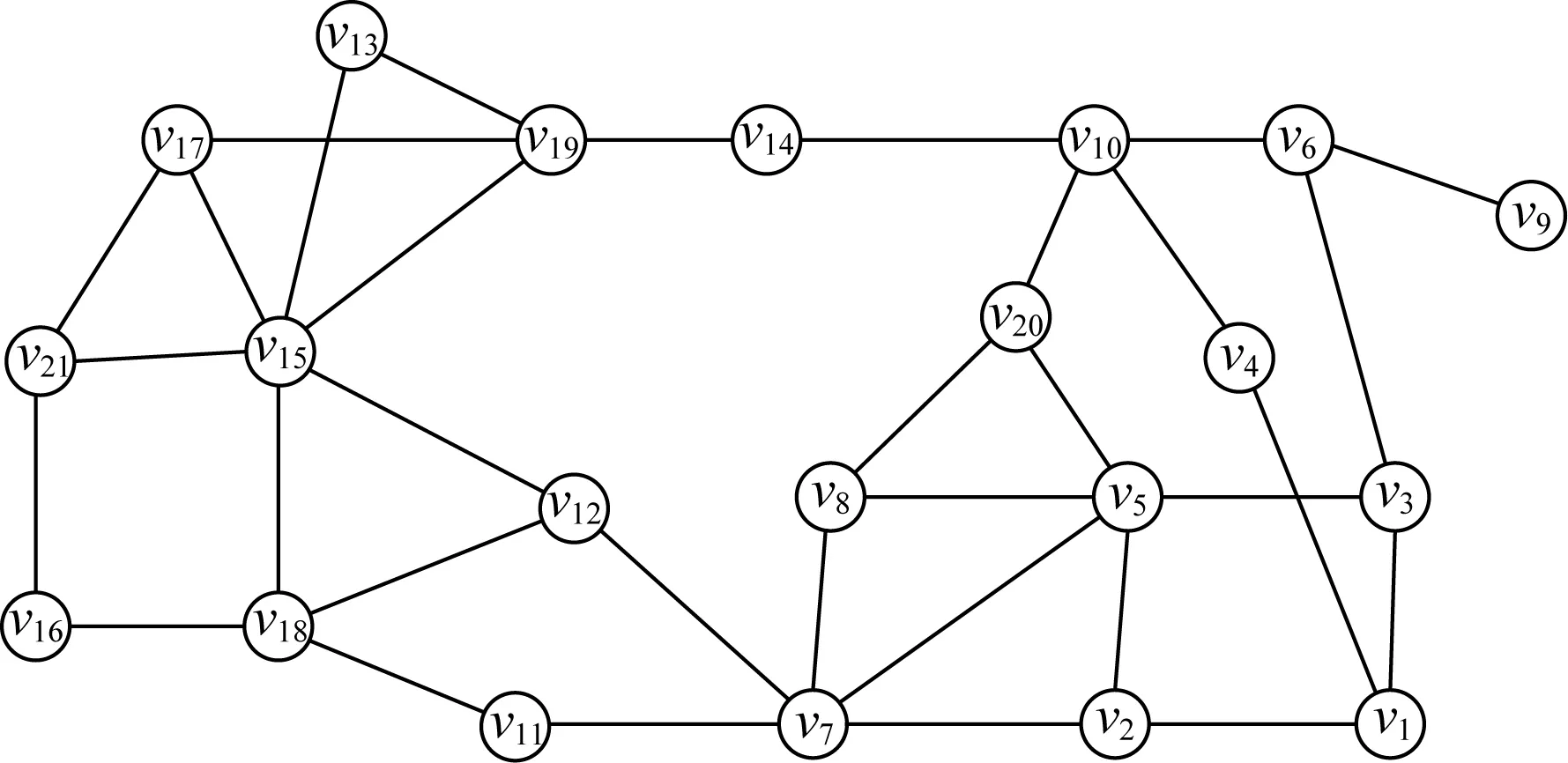
Fig. 1 The topological structure of an example network图1 示例网络的拓扑结构
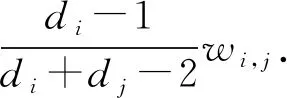
(5)
其中Г(vi)是节点vi的邻居节点集合,di为节点vi的度数,wi,j为式(4)给出的(vi,vj)的权重.可以看出,一条边对其关联度数较高的节点权重贡献更大.
式(5)所定义的局部邻域中心性指标LNC,综合考虑了节点的度信息及其邻域节点间的拓扑结构.
表2给出了图1所示网络在一些经典中心性度量指标下排名最高的4个重要节点集合S,以及从网络中删除S后对应的连通分支数和连通节点对数f(S),可以看出本文给出的LNC指标表现出良好的性能.
在第5节,将利用度中心性、LocalRank中心性、 K壳中心性、局部度和中心性与本文所提的LNC指标在GCNP(σ)算法框架下生成初始点覆盖集S,比较它们在人工网络和真实网络上对网络连通性的影响.
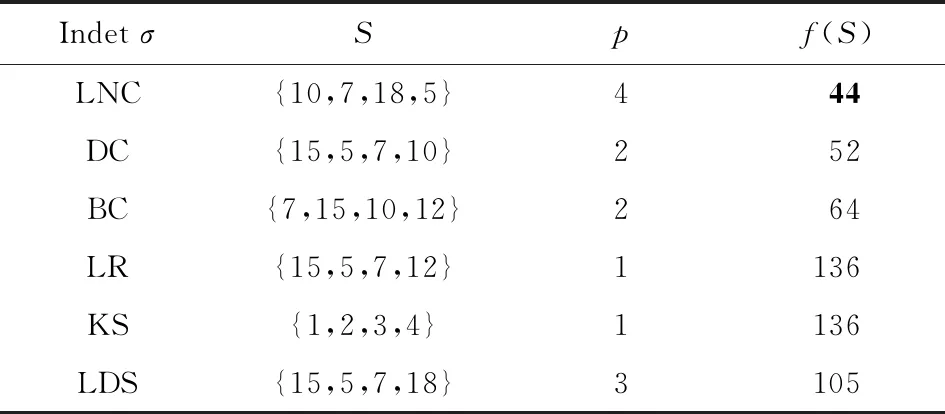
Table 2 Critical Node Sets Determined by Index σ onExample Network表2 示例网络上按指标σ选取关键节点集结果
Note:S—the critical node set;p—connected component number in the residual graphG[VS];f(S)—the pairwise connectivity ofG[VS].
5 实验与结果
在人工网络数据集[23]和真实网络数据集上对本文所提算法框架GCNP和LNC指标做有效性验证.人工网络数据集包括16个人工网络,依据不同的网络结构可以分为4种类型,网络节点数为250~5 000不等,具体信息见表3.参数k的选取范围是k∈{5,10,20,30,50,75,100,150,200,300,500,1 000,1 500,3 000}且k<|V|.排除掉删除k个节点后所得的网络中不存在连通的点对的情况,可以得到人工网络与不同k组合共156个案例.
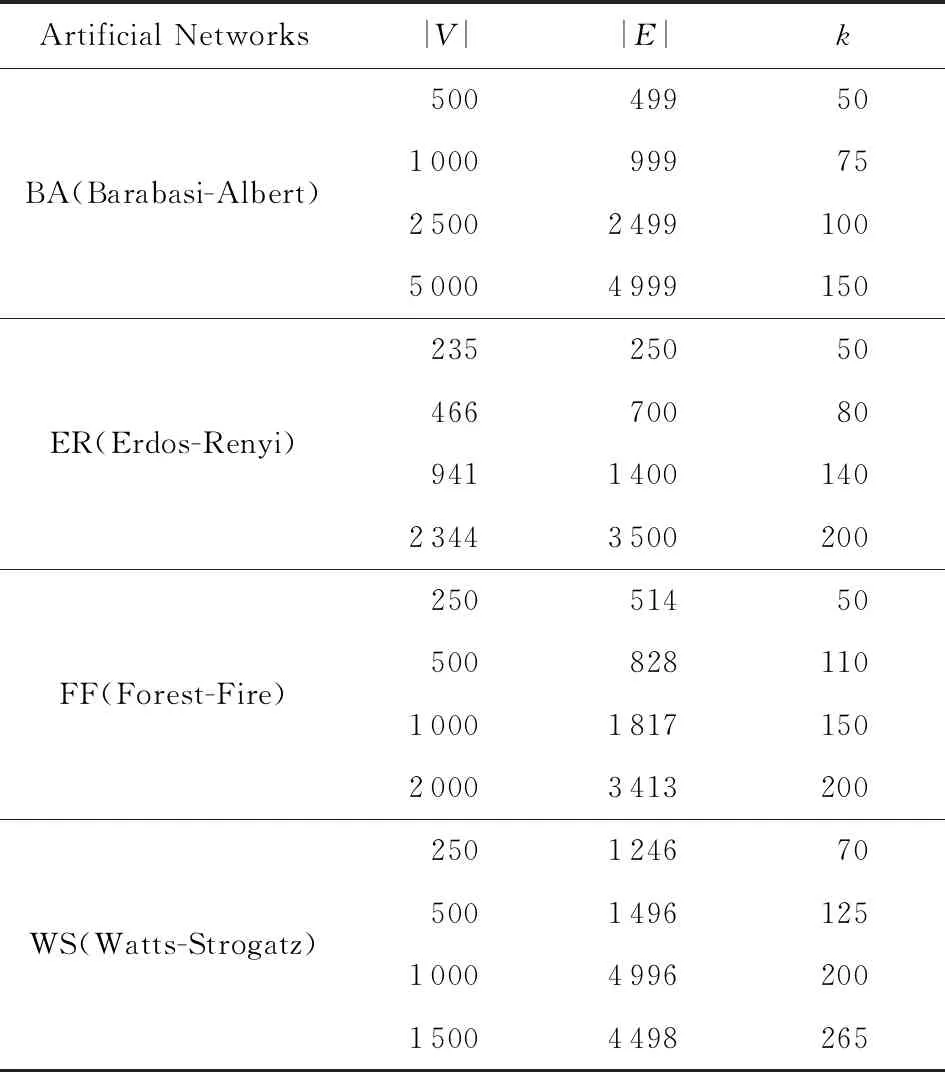
Table 3 Artificial Network Datasets[23]表3 人工网络数据集[23]
Notes:|V|—node number; |E|—edge number;k—a preset integer, it determines the size of the critical node setS.
真实网络数据集包括9个真实世界网络,具体网络信息见表4.考虑到真实网络的复杂性,在此根据删除节点占网络节点总数的比值确定参数k,具体为:k∈{0.01|V|,0.05|V|,0.1|V|,0.15|V|,0.2|V|,0.25|V|,0.3|V|}.排除掉删除k个节点后所得的网络中不存在连通的点对的情况,可以得到真实网络与不同k组合共72个案例.
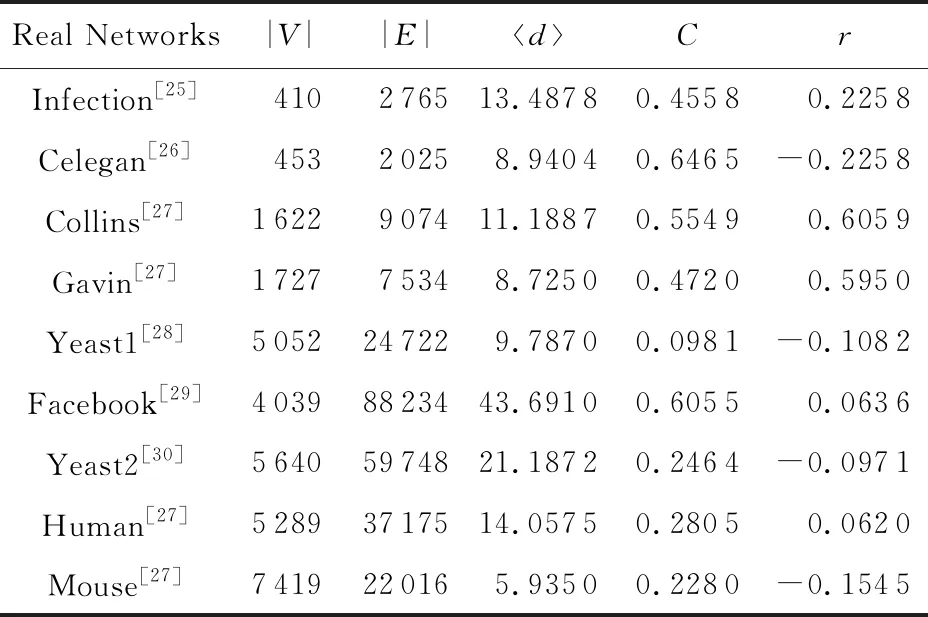
Table 4 Real Network Datasets表4 真实网络数据集
Notes:|V|—node number; |E|—edge number;d—average degree;C—clustering coefficient;r—degree assortativity.
采用文献[31]给出的效能函数对算法性能进行评价.算法A在测试数据集所有案例集合T上的效能函数定义为
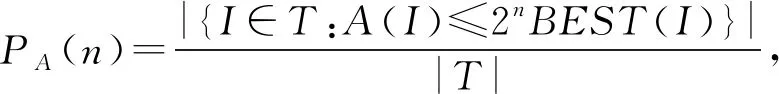
(6)
其中,A(I)表示算法A在某一案例I上的结果,在本文中A代指在GCNP框架下所对应的各个指标,BEST(I)表示在案例I上所有对比算法中获得的最好结果.效能函数曲线上的点(n,PA(n))表示算法A的计算结果与最优结果的相对误差不超过2n-1的情况下测试案例所占比例.可以看出相对误差是关于n的指数函数,表5列出了n∈[0,0.6]时相对误差的取值.
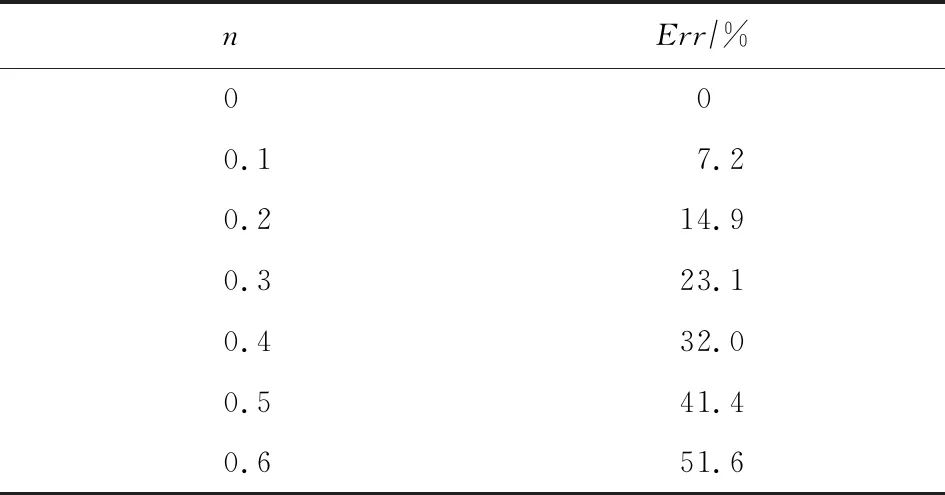
Table 5 Relative Errors of Performance Profile (n∈[0,0.6])表5 效能函数相对误差(n∈[0,0.6])
当评价算法A和A′的性能时,如果算法A的效能函数曲线位于A′效能函数曲线的左上方,则认为算法A优于算法A′.
图2给出了GCNP(σ)算法分别在人工网络数据集和真实网络数据集上的效能函数曲线图.从图2(a)所示人工网络数据集上的函数曲线,可以看出本文所提局部中心性指标LNC在关键节点识别方面表现良好.当n=0(相对误差为0%)时,算法GCNP(LNC)在49%的人工网络案例上达到最好的效果,明显优于其他指标.当n=0.14(相对误差为10%)时,GCNP(LNC)在将近91%的案例上达到较好的效果,也明显优于其他指标.

Fig. 2 The curves of performance profiles of GCNP(σ) under 5 centralities图2 GCNP(σ)在不同指标下的效能函数曲线
在真实网络数据集上也可以得到类似的结论.如图2(b),当n=0(相对误差为0%)时,算法GCNP(LNC)在26%的人工网络案例上达到最好的效果,明显优于其他指标.当n=0.14(相对误差为10%)时,GCNP(LNC)在将近76%的案例上达到较好的效果,也明显优于其他指标.
表6给出了算法GCNP(σ)在人工网络数据集和真实网络数据集部分案例上对应的5个中心性指标上重复实验30次所得的最佳结果.可以看出,通过删除由算法GCNP(LNC)所得到的关键节点集合能够使大多数网络上剩余图上连通节点对数达到最小.
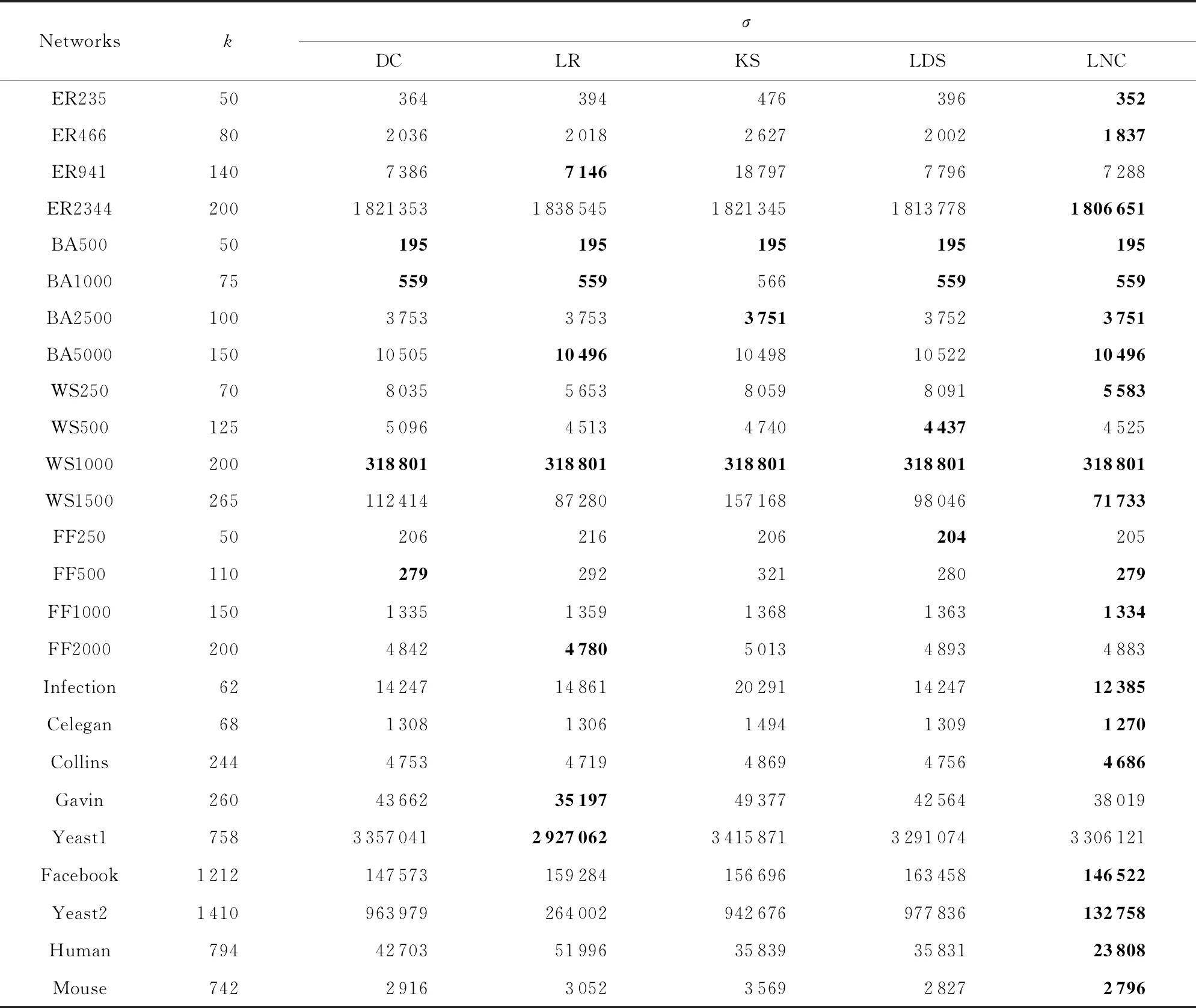
Table 6 Pairwise Connectivity of GCNP(σ) on 5 Centralities表6 GCNP(σ)算法在各中心性指标下所得的连通节点对数
Note: The best results are in bold.
6 总 结
本文提出了一种基于节点中心性的网络关键节点识别搜索框架GCNP,根据某种中心性指标选择网络的初始点覆盖集;从网络中删除该点覆盖集,迭代选择点覆盖集中使网络连通节点对增加最小的节点向原网络回添,直至点覆盖集中节点满足用户给定的待删除关键节点数.为了更好地选择初始的节点覆盖集,本文还提出了一种基于局部拓扑结构特征的节点中心性度量指标LNC.在16个人工网络和9个真实网络上的实验结果表明,采用GCNP算法可以提高算法性能.本文所提的节点中心性度量指标LNC较度中心性、LocalRank中心性、K壳中心性、局部度和中心性更能准确地评估节点的重要性.
近年来,复杂网络呈现出大规模和动态性的特点,如何设计合理的算法以有效识别大规模动态复杂网络中的关键节点是CNP问题面临的一大挑战.我们也将就这一问题开展深入探索.

