主动防御的最优预测协同制导律研究*
史 恒,朱纪洪
0 引 言
飞行器在应对来袭导弹攻击威胁时,传统的对抗手段主要包括施加电磁干扰、释放红外诱饵、以及自身机动摆脱等被动的防御技术.随着进攻武器的抗电磁与诱饵干扰的能力、自身的机动能力越来越强,传统的被动式防御战术已难以适应空中作战需求,不足以为飞行器提供有效的安全保障.此时,飞行器可以通过主动防御形式来实现自我保护,即主动发射防御型导弹来拦截来袭导弹.主动防御的概念早在40多年前就被提出,但至今仍未能够在飞行器上应用.事实上,主动防御系统已在坦克、舰船、直升机等平台有一些成熟的应用和试验验证,而随着机载系统的逐渐小型化,主动防御在飞行器上取得应用也成为一个势在必行的趋势.
主动防御的数学模型是三体对抗模型,也就是:载机,来袭导弹,防御导弹三个物体构成的对抗场景.来袭导弹瞄准载机进行制导攻击,载机在机动躲避来袭导弹的同时发射防御导弹对来袭导弹实施拦截.主动防御问题既包含了防御导弹对来袭导弹的拦截制导、又包含了载机对来袭导弹机动规避,在制导与控制领域是一个值得深入研究的问题.主动防御问题求解的主要任务是设计防御导弹的制导律,它应是一个鲁棒的、能够实现对全向来袭目标的高效高概率拦截.在制导问题中最常用的最优制导律是比例导引(PN)制导律.为了达到较好的拦截效果,PN制导律通常要求拦截弹拥有比目标弹3倍以上的机动性能.在三体对抗任务中如果攻防双方都使用PN,理论上来说防御导弹至少需要具有载机9倍以上的机动能力.但实际上,防御导弹受限于尺寸等条件,其机动能力通常会劣于进攻导弹.因此直接使用PN制导律在主动防御场景中是不合适的.
在最近的十几年里,主动防御问题在国内外受到了广泛的关注.在防御导弹制导律的研究上,主要通过最优控制理论[1-11]、微分对策理论[12-14]、视线角(LOS)制导[15-16]和滑模制导[17-19]等方式开展.然而,大部分的制导律研究都是在二维平面中进行的推导,且都采用了线性化的近似假设,对于主动防御这样一个非线性场景,距离实际的工程实现还比较远.在很多主动防御的制导律研究中,对来袭导弹信息的获取都需要包含具有机动加速度的完美信息,而这在实际场景中是难以获得的,一些文章中采用滤波和辨识方法来估测得到这一信息[11, 20].主动防御问题不同于传统的一对一制导问题,来袭导弹的追踪目标是载机,载机可与防御导弹协同进行拦截,其加速度信息会耦合在三体运动关系中,因而有一定的可预测性.本文研究的预测制导策略将通过解算三体的运动关系,预测防御导弹与来袭导弹的未来预期拦截点,从而跳过了来袭导弹的加速度估测,再以预期预测点为目标进行制导.
本文的工作旨在更加接近主动防御实际非线性工况的基础上,提出一种高效的、易于实现的三维制导策略,相对于前述工作具有更少的理想化假设,使得即使在防御导弹的速度和机动过载性能弱于来袭导弹时也能够成功完成拦截.由于当今电子技术的进步,机载设备的小型化已经越来越成熟,计算性能已大大增加,因此考虑在假设已经具有高性能弹载制导计算机的基础上,将传统的PN制导律结合计算制导计算方法[21]作为预测基础,以简单的实现方式实现高效拦截.通过数值仿真可以验证提出的预测制导律相对于传统方法,具有更小的需求过载,脱靶量更小,制导能量损耗更小,拦截包线更大.
1 主动防御问题数学模型
1.1 主动防御场景
由载机、来袭导弹和防御导弹构成的主动防御三体模型如图1所示.
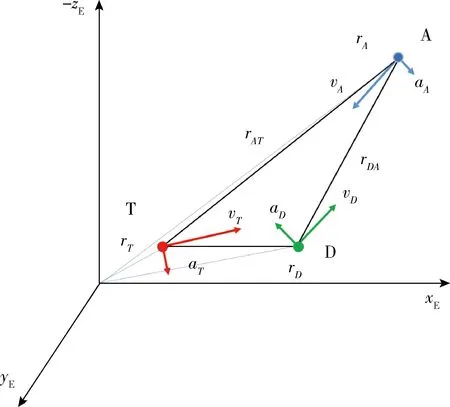
图1 主动防御三维数学模型Fig.1 3-dimensional active defense geometry
考虑主动防御场景下的三方:载机(T)、来袭导弹(A)和防御导弹(D)都在惯性坐标系下,防御导弹由载机发射以拦截来袭导弹.定义主动防御三体的状态向量:
xi=[ri,vi,ai]T,i={T,A,D}
(1)
其中ri,vi,ai分别为三运动体的位置、速度与法向加速度.
在主动防御任务的实际情况中,作为防御方,载机的飞行状态完全可通过机载设备测得,其未来的机动加速度也可由飞行策略给出;防御导弹的状态也可由弹载设备测得;来袭导弹的位置和速度信息可通过机载雷达测得,但机动加速度不可测.
每个飞行器的运动学模型为:
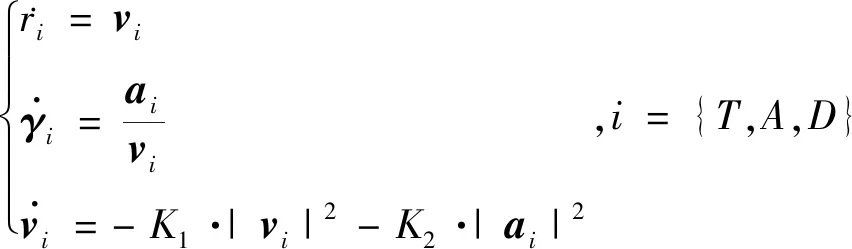
(2)
其中,γ为航向角,K1、K2为两个速度衰减系数且均为正.
注:为了更加贴近实际工况,此处为飞行器的速度引入了两个非线性衰减项.第一项考虑了气动阻力,速度的衰减与速度平方呈正比;第二项考虑制导带来的速度衰减,与制导法向过载的平方呈正比.
在该模型中存在两组对抗关系,包括为来袭导弹A和载机T的对抗,以及防御导弹D与来袭导弹A的对抗,分别用下标“AT”和“DA”表示,从而可以定义二者的相对位置和相对速度:
rAT=rT-rA
(3)
rDA=rA-rD
(4)
vAT=vT-vA
(5)
vDA=vA-vD
(6)
针对主动防御拦截任务的需求,防御导弹应保证载机的安全,因而防御导弹需要在来袭导弹拦截到载机之前首先拦截到来袭导弹.定义tf为拦截持续时间,则主动防御拦截的时间约束为
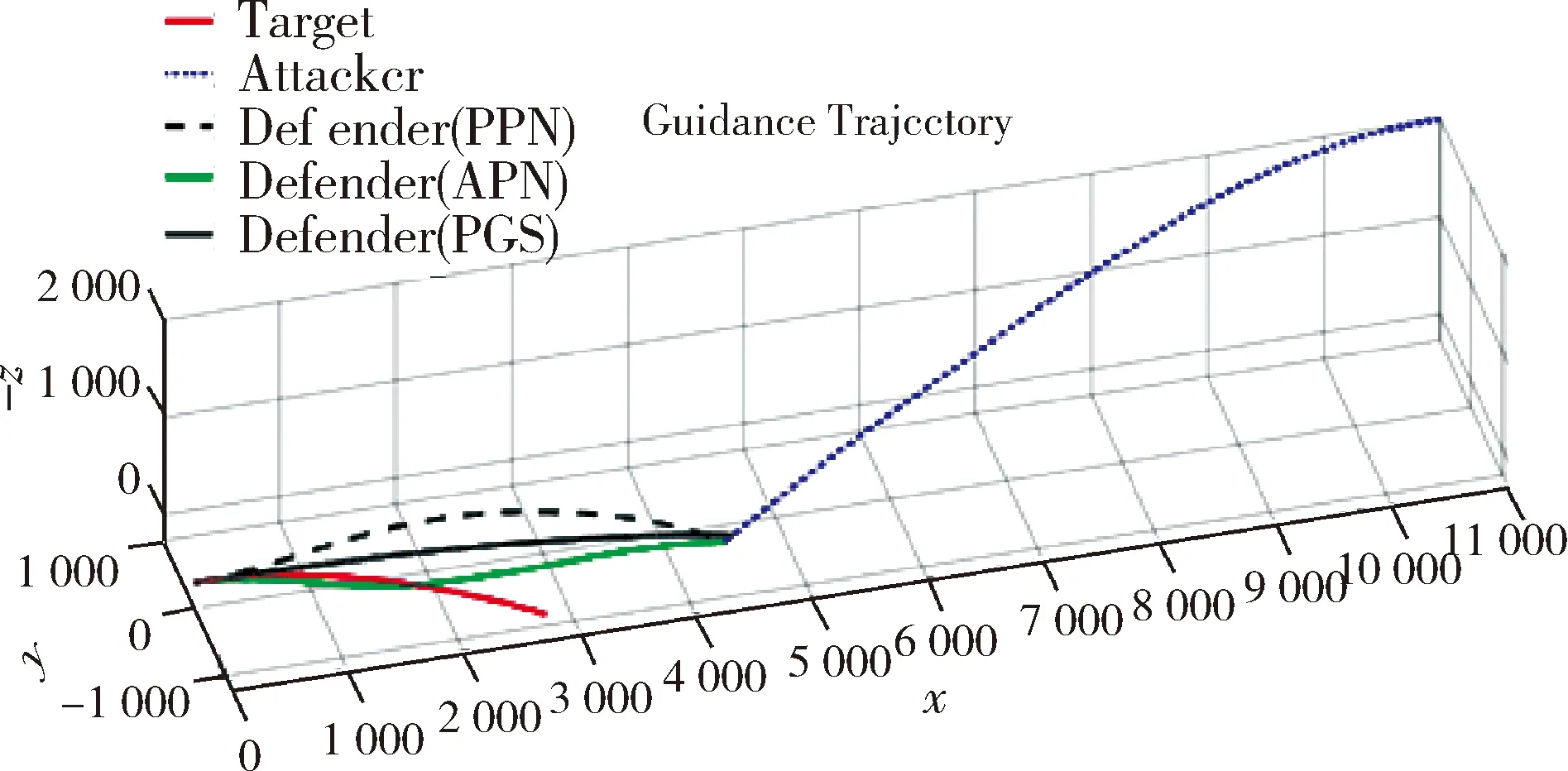
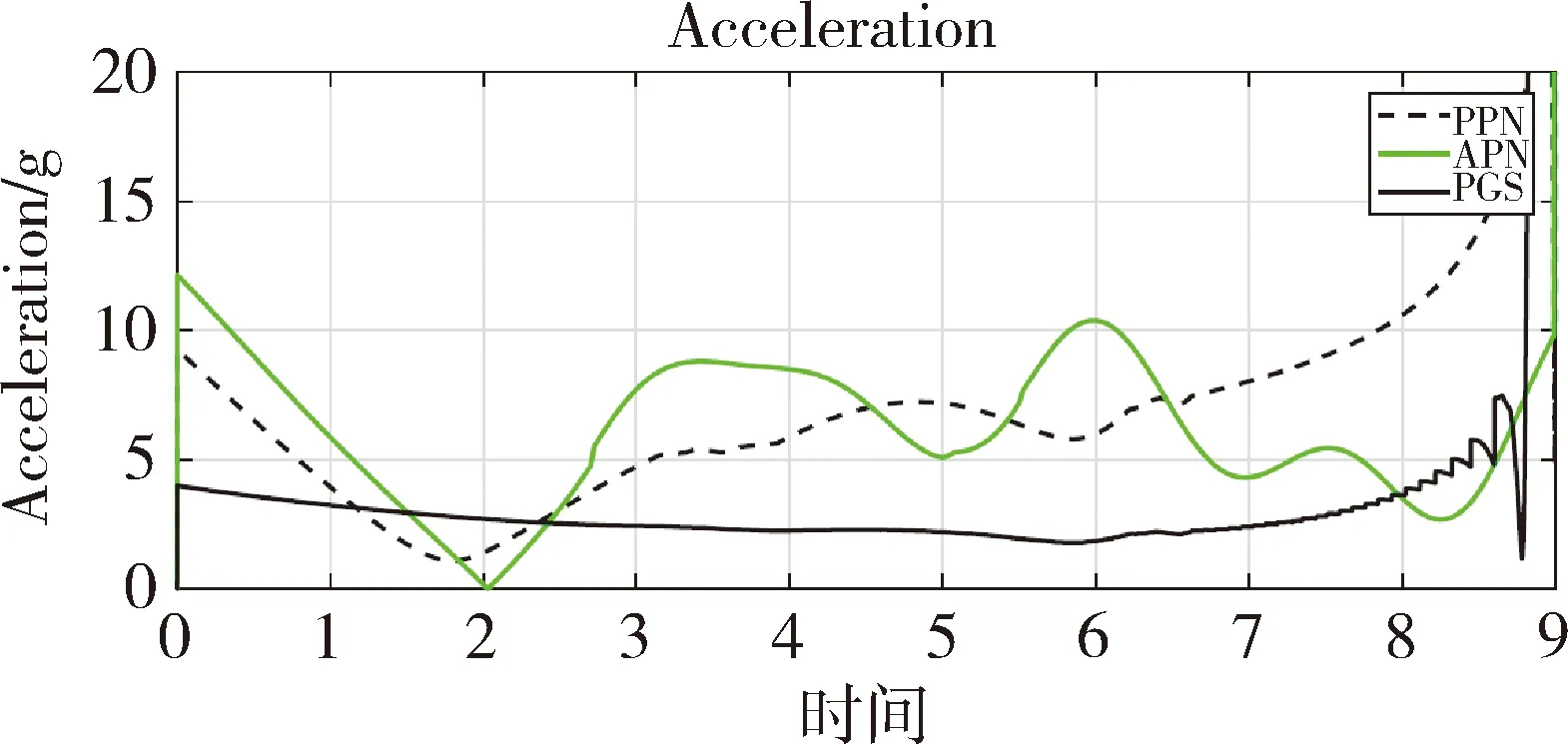
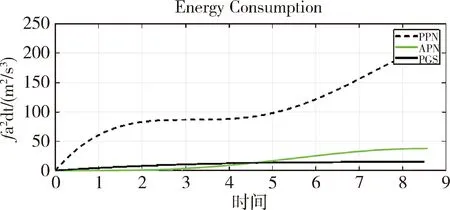
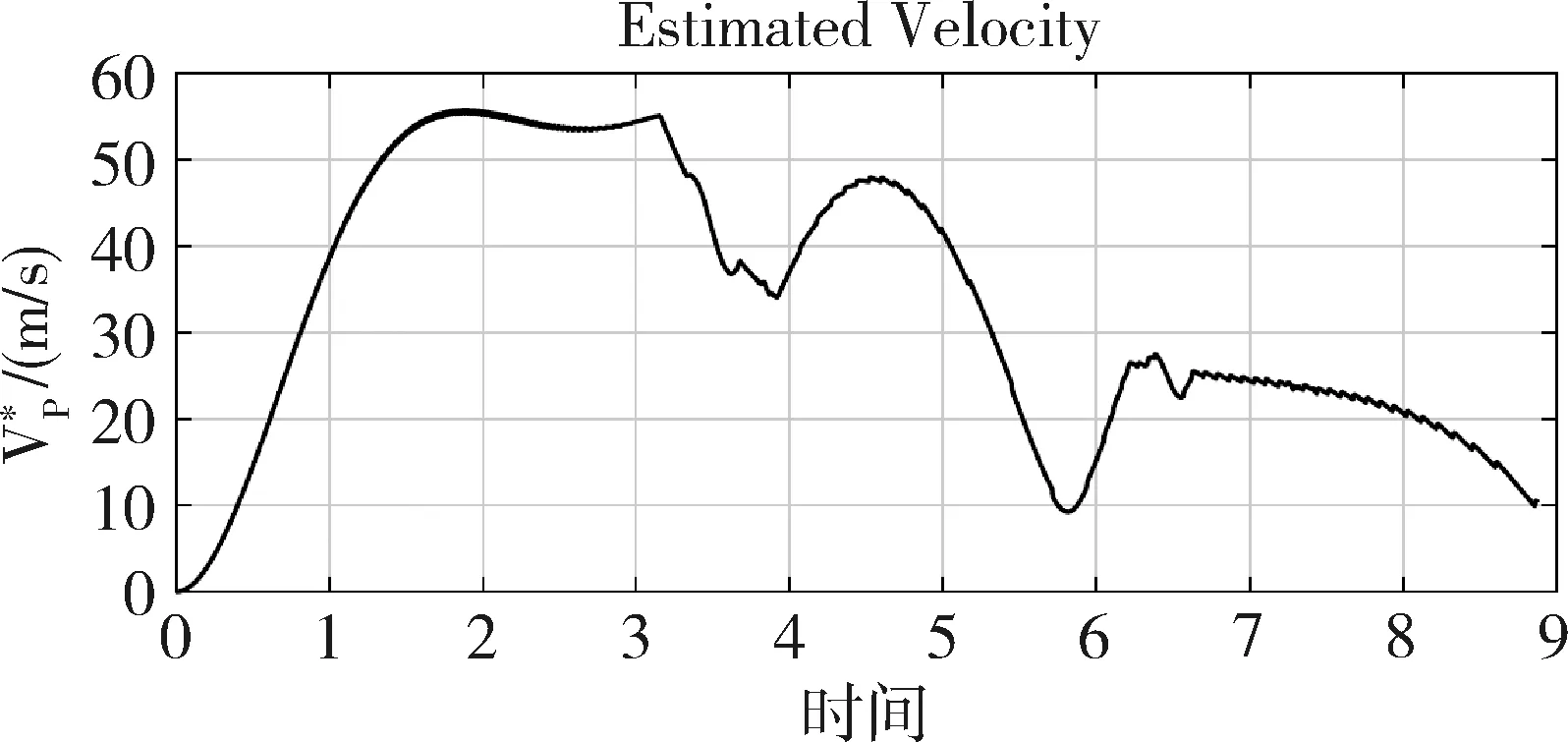
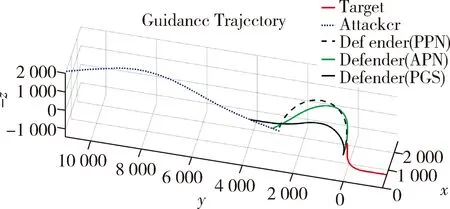
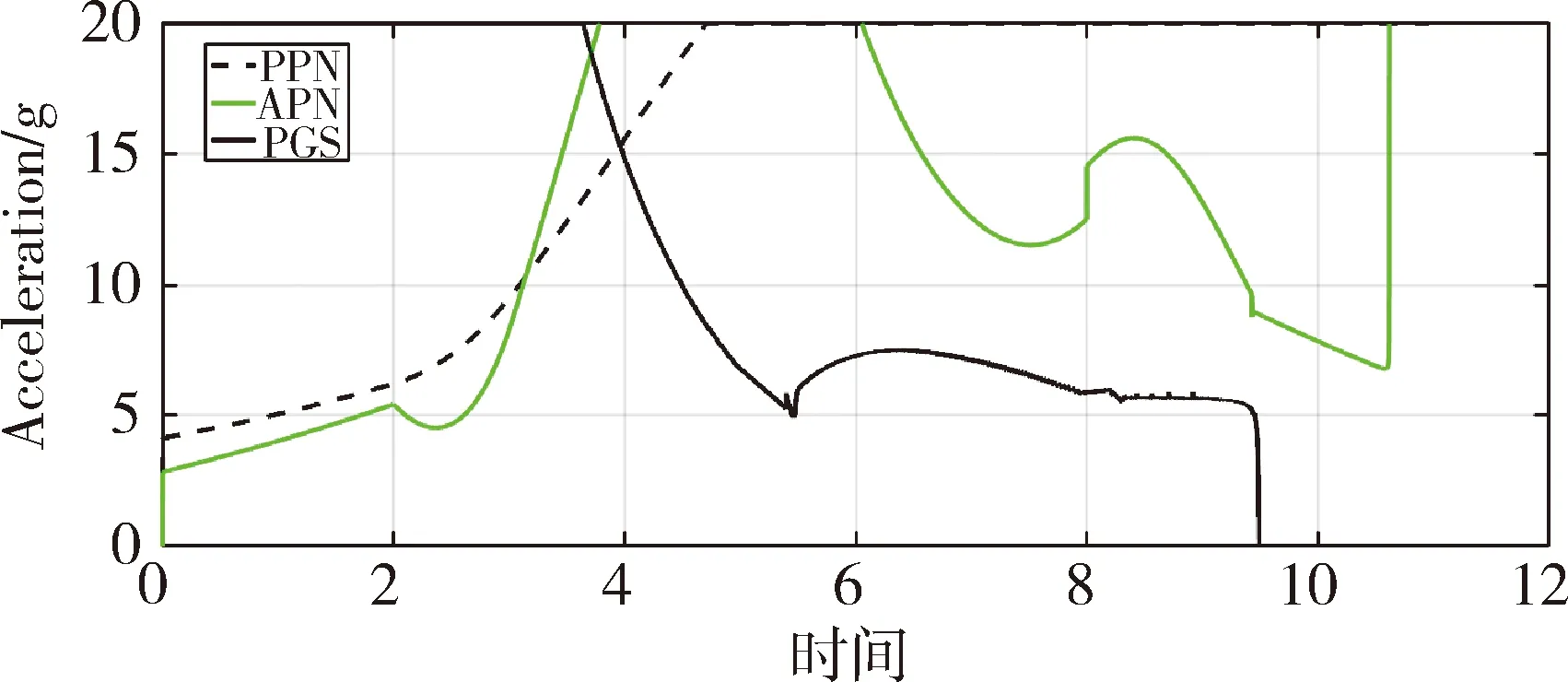
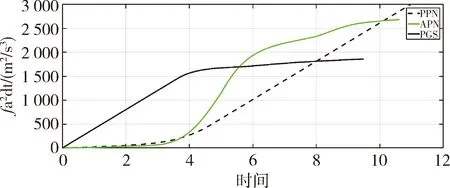
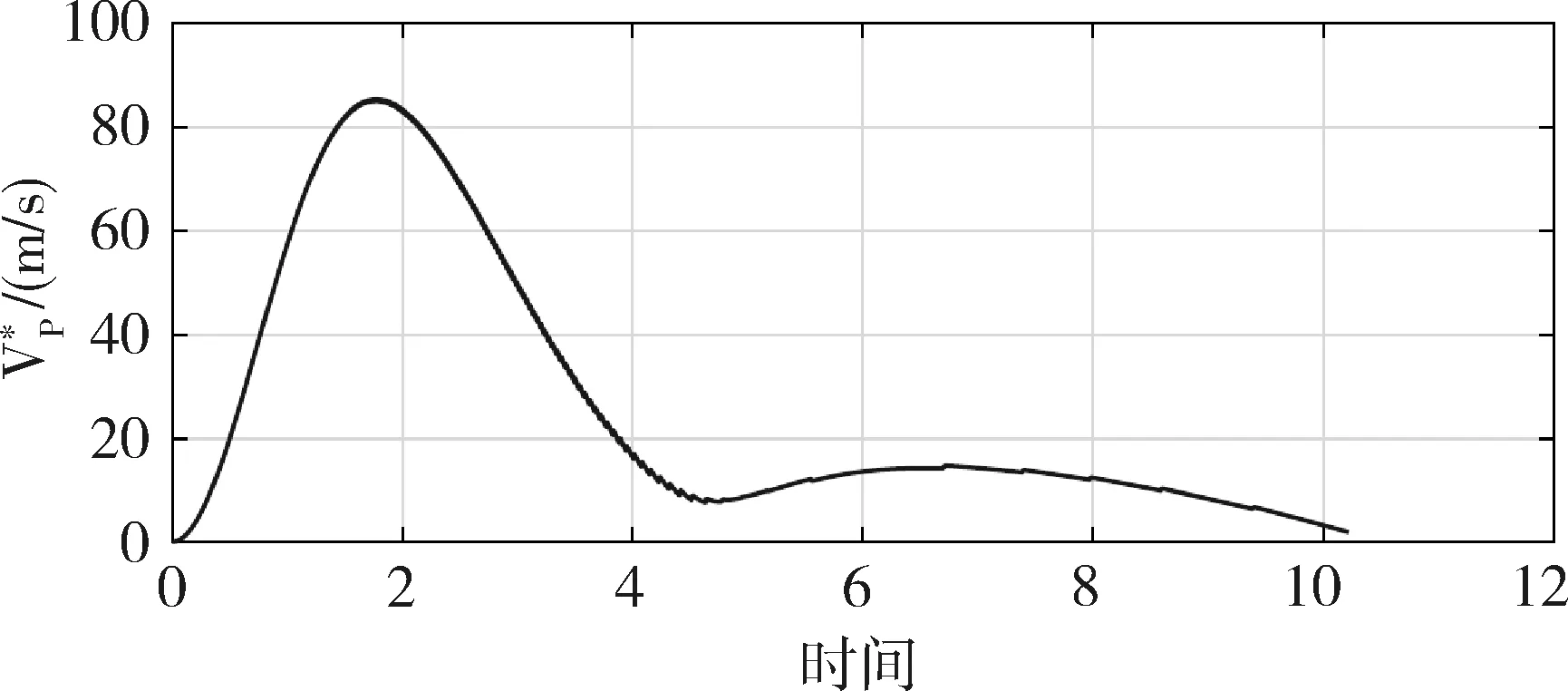
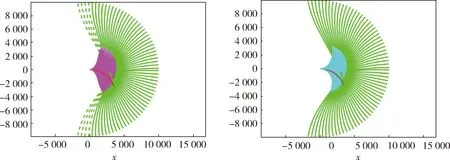
tf,AD (7) 根据主动防御场景,对三个飞行器的性能作如下假设: (1)不考虑制导指令的时延; (2)来袭导弹的初速度大于防御导弹,且两导弹的速度均大于载机,即 |vA(0)|>|vD(0)|>|vT(0)| (8) (3)制导指令过载沿垂直于速度方向,过载能力有界且满足 (9) 同时,三者的过载加速度能力与速度类似,为 (10) 在预测计算中将使用等加速度模型对运动状态进行积分: i={T,A,D} (11) 其中dt为时间步长. 本文中的预测制导律基于扩展比例导引律(APN)得到,以防御导弹D对来袭导弹A进行拦截为例,三维场景中防御导弹的APN制导律为: (12) (13) (14) (15) 协同预测制导律同时考虑载机、来袭导弹、防御导弹三体的实时状态信息,在融合预测模块使用迭代计算方法积分得到D对A的预测拦截点.由于三体对抗模型中可能存在测量误差,以及对来袭导弹制导律估测与辨识的不准确,预测拦截点的实时位置也将存在偏差,也就是说预测拦截点的位置是时变的,因此可将预测拦截点看作一个虚拟的运动目标P*,防御导弹再对虚拟目标设计制导律.在拦截过程中,虚拟目标的移动速度远小于来袭导弹,可通过滤波估计得到,因而拦截高速来袭导弹的任务被转化为了拦截低速等效虚拟目标的任务,可实现更好的拦截效果,防御导弹也会消耗更少的能量实现制导. 协同预测制导的流程图如图3所示. 需要注意的是,在计算预期拦截点时,我们假设了A也采取APN制导律来追踪T,实际上是无法得知的,A可以采取任何可能的制导律来进攻T.也就是说,此时预测的P*并非真实的未来碰撞点,将存在一个误差值.但由于预测过程是弹载制导计算机实时计算的,预测点的计算误差也会由于制导律反馈的本质随着实时计算逐渐减小而消除,最终使得拦截发生. 图2 主动防御协同预测制导律示意图Fig.2 The block diagram of the Cooperative Prediction guidance law 图3 主动防御协同预测制导律流程图Fig.3 The flow chart of the Cooperative Prediction guidance law 关于协同预测制导律的收敛性讨论: 在某些状态下,例如制导过程的前置偏差角过大时,防御导弹采用APN法可能无法拦截到来袭导弹.按照预测制导律对于预期拦截点的计算方法,此刻的虚拟目标位置仍应选为rA,k+n点,即未来时刻D与A位置最接近的点,在下一时刻瞄准此位置进行制导仍有可能完成拦截.对于这种瞬时预测无法成功拦截的目标,预测制导将保证防御导弹使用最大机动能力进行转弯.因而,预测制导律能够完成比APN更多工况的任务,预测制导律的边界即为防御导弹最大机动能力所到达的边界.只要来袭导弹在防御导弹能够到达的最大范围内,预测制导律均可收敛. 得到虚拟目标的位置后,其运动速度可通过卡尔曼滤波得到.根据公式的(9)等加速度模型,滤波模型为: xP*,k=FxP*,k-1+vk yk=CxP*,k+wk (16) 其中xP*,k为tk时刻虚拟目标P*的状态,yk为测量值即P*在tk时刻的位置.F为状态转移矩阵 (17) C为观测矩阵 C=[I30 0] (18) vk为过程噪声,wk为“测量”噪声,在这里可以理解为在预测过程中造成的误差,假设预测造成的误差大于过程噪声. 应用卡尔曼滤波公式迭代 (19) 从而可以估计虚拟目标的速度为 vP*=[0I30]xP* (20) 为了验证主动防御协同预测制导律的有效性,本节开展了两组数值仿真. 为简便起见,本文提出的预测制导法(Predictive guidance strategy)简称为“PGS”.在仿真中作为参照对比的制导律选取经典的纯比例导引律(PPN),以及扩展比例导引律(APN). 三种飞行器的初始速度分别为: VT=300 m/s,VA=800 m/s,VD=500 m/s 其最大法向过载能力分别为: 为精确计算脱靶量,仿真步长选取为10-5s,制导步长为0.05 s.在制导与预测模块中,对相关参数的选取如下:制导律系数N=3;过程噪声矩阵V=0.1·I3,测量噪声矩阵W=I3. 场景1迎头工况: 来袭导弹从载机的迎头方向11 km处来袭;载机在初始状态从原点处出发,沿x方向飞行,同时进行规避机动;防御导弹由载机在原点位置发射,发射方向与载机飞行方向相同,即x方向.来袭导弹使用系数时变的APN制导律向载机进攻,比例系数: NA=4+sint (21) 其中,t为仿真时间. 为了尽可能地与真实场景相符,在主动防御任务中,载机需要采取有效的逃逸措施来对来袭导弹进行规避.此处载机的机动选用[10]中的最优逃逸策略,即aT=5 g,向-y方向机动,以最大程度地增加A对T制导的脱靶量. 场景1的仿真结果如图4~图7所示,拦截脱靶量如表1所示.可以看出,预测制导律相对于其它方法的拦截弹道更加平直,制导过载和制导的能量消耗也都远小于其它方法,脱靶量也更小.图7为预测模块对预测虚拟目标的速度估测,其平均速度不到30 m/s,远小于制导原目标即来袭导弹的800 m/s.此外,本仿真也验证了在来袭导弹制导模型与预测假设存在偏差时,预测制导算法仍是有效的. 图4 迎头来袭情况下预测制导律与PPN法、APN法的拦截弹道对比Fig.4 Trajectories comparison of Scenario 1 场景2侧向工况: 来袭导弹从载机的左方11 km处来袭;载机在初始状态从原点处沿x方向出发;来袭导弹使用与场景1相同的变系数APN制导律.此外,防御导弹制导中对来袭导弹位置速度的测量加入了均值为0,方差为10的高斯白噪声. 图5 迎头来袭情况下预测制导律与PPN法、APN法的制导过载对比Fig.5 Accelerations of the Defender in Scenario 1 图6 迎头来袭情况下预测制导律与PPN法、APN法的制导能耗对比Fig.6 Guidance energy consumption in Scenario 1 图7 迎头来袭情况下虚拟目标的速度估测Fig.7 Estimated velocity of virtual target in Scenario 1 在此场景中,载机使用空战对抗中的一种标准机动动作——破S(Split S)机动来躲避具备高度和速度优势的来袭导弹.如图8所示,载机轨迹为红线,首先沿x方向出发,然后使用最大过载俯冲至速度沿z方向向下,紧接着用最大过载改变航向至速度沿-y方向. 场景2的仿真结果如图8~图11所示.可以看出在使用PPN和APN时,交战起初的视线角速度很小,导致制导过载一开始很小,随着来袭弹的逼近才逐渐增大,因而拦截弹道相对较长,不但耗费了较多能量,最终拦截的脱靶量也较大,PPN由于过载饱和无法实现拦截.而使用预测方法,防御导弹在开始阶段就以较大过载进行转弯,后来慢慢平稳减小,能够取得较好的拦截效果.使用PGS的拦截弹道也相对平直,因而其拦截持续时间也小于其它方法,这也满足了主动防御任务对于尽早完成拦截任务的时间约束需求. 引入预测思想后,对制导过载的优化能够使得防御导弹尽早实现转弯,从而扩大拦截包线范围,图12是比例导引律与预测制导律的拦截区域对比.左图为使用比例导引律的各向拦截弹道,绿色实线部分代表能够成功完成拦截的弹道,虚线部分代表脱靶量较大无法拦截.使用比例导引律的拦截范围为±89°.而使用协同预测制导律,拦截范围可扩大到±110°. 图8 侧向来袭情况下预测制导律与PPN法、APN法的拦截弹道对比Fig.8 Trajectories comparison of Scenario 2 图9 迎侧向来袭情况下预测制导律与PPN法、APN法的制导过载对比Fig.9 Accelerations of the Defender in Scenario 2 图10 侧向来袭情况下预测制导律与PPN法、APN法的制导能耗对比Fig.10 Guidance energy consumption in Scenario 2 图11 侧向来袭情况下虚拟目标的速度估测Fig.11 Estimated velocity of virtual target in Scenario 2 表1 拦截时间与脱靶量Tab.1 Interception time and miss distance 图12 比例导引律与预测制导律拦截区域对比Fig.12 Comparison of interception area between PN law and PGS law 针对主动防御问题,本文提出了一种三维的协同预测制导律,将迭代计算与经典制导律相结合,实时预测拦截点,将拦截高速来袭导弹的问题转化为拦截低速虚拟目标问题,从而提升了拦截性能.仿真结果表明,使用协同预测制导律能够优化防御导弹的制导过载,降低最大过载需求,取得较小脱靶量的同时也能更加节省能量.在应对大前置角偏差的工况时,能够帮助防御导弹实现快速转弯,更快完成拦截,从而增加主动防御系统的拦截范围.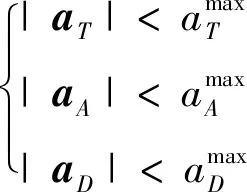
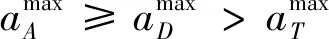
1.2 制导律模型
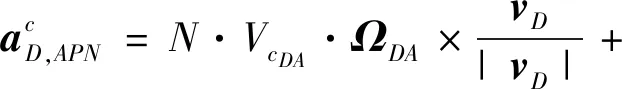
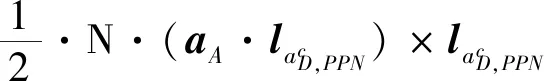
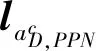
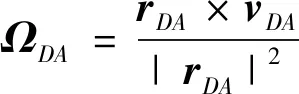
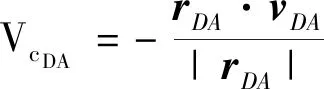
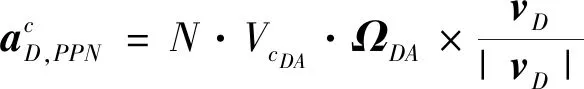
2 协同预测制导律
2.1 预期拦截点的计算
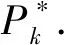
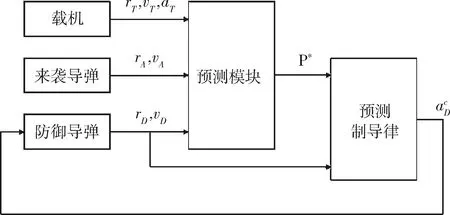
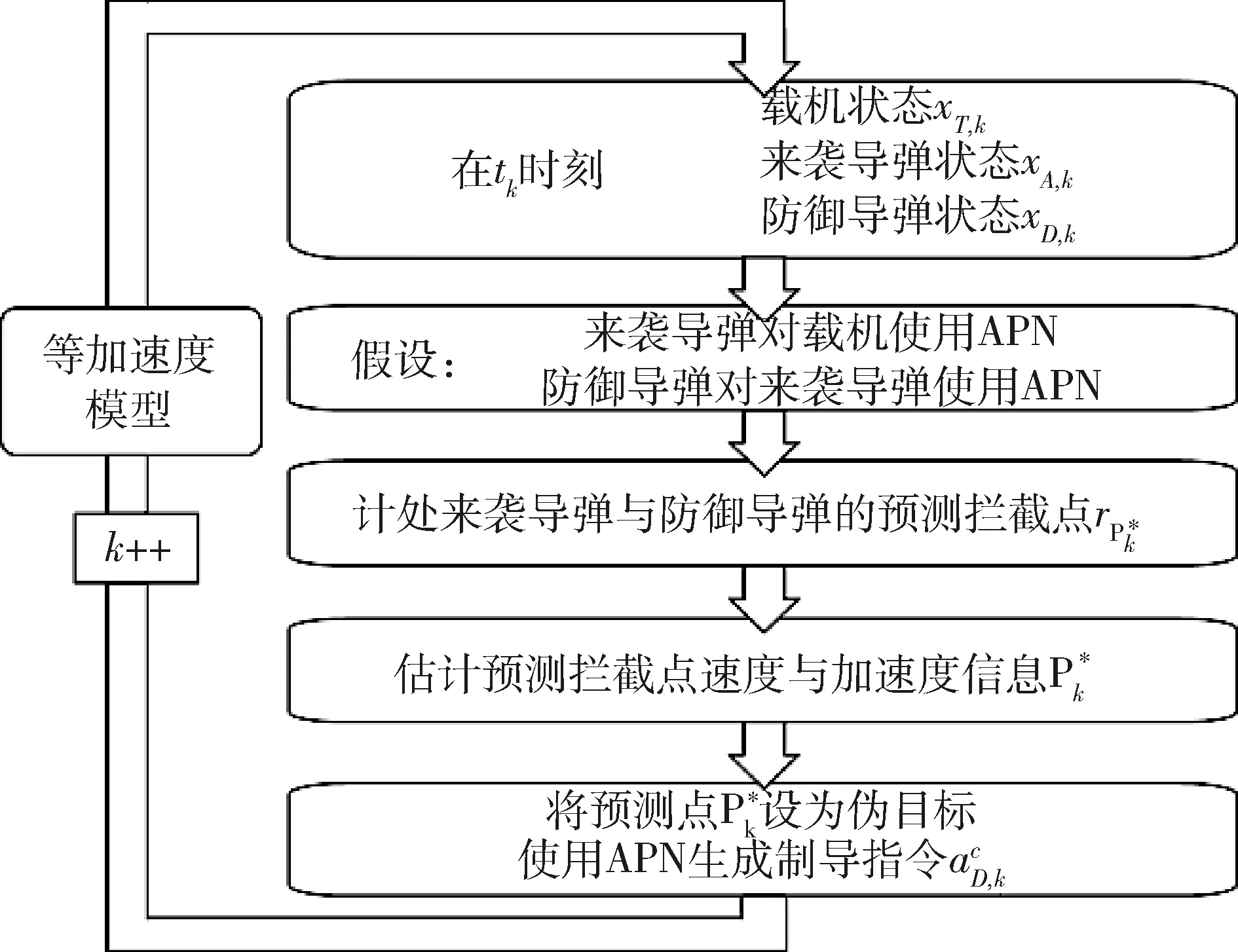
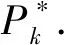
2.2 虚拟目标状态估计
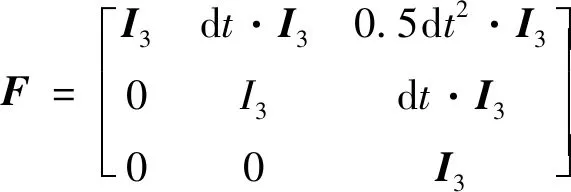
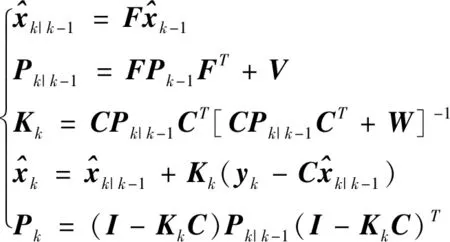
3 仿真算例

4 结 论

