具有指定性能和全状态约束的多智能体系统事件触发控制
杨彬 周琪 曹亮 鲁仁全
随着工业和军事应用的发展,愈来愈多的工作需要多个智能体协同完成,因此多智能体协同控制迅速成为学界的热门课题[1−8].由于多智能体协同控制只需接收智能体之间的局部信息,从而大大降低了系统的通讯成本和能耗,且具有更好的灵活性和鲁棒性,所以广泛应用于多机器人协同控制、无人机编队和传感器网络等领域.多智能体协同控制主要包括一致性问题[1−6]、集群问题[7]、编队问题[8]等.其中一致性跟踪问题作为协同控制的一项基本问题,受到了学者们的广泛关注[1−5].
在多智能体系统中,每个智能体的微处理器一般会受到计算能力和通信带宽的限制,因此如何在多智能体的一致性跟踪控制过程中降低通讯成本、减小计算压力成为了亟需解决的问题.针对这一问题,有学者在控制器中加入了事件触发机制,并获得了显著的成果[9−12].但是,事件触发机制可能发生奇诺现象,即触发事件会在有限时间内被无数次触发.为了解决这一问题,文献[13]研究了几种不同事件触发机制的最小事件触发时间间隔的基本性质.文献[14]则结合自适应控制解决了事件触发控制中输入状态稳定性的问题.将事件触发机制加入到控制器设计中显著降低了控制过程的能耗和成本,因此,事件触发控制成为了多智能体一致性跟踪控制的一种重要方法.
由于受到物理器件和运行条件的限制,系统通常需要对其状态进行约束,否则将会导致系统不稳定、性能急剧下降等现象,甚至会造成重大的安全事故.因此,解决系统的状态约束问题意义重大.全状态约束作为一种常见的状态约束形式,一直是控制领域的研究热点与难点.文献[3,15−16]均使用Barrier Lyapunov 函数对具有全状态约束的系统进行了研究.文献[15]研究了一类具有参数不确定性的非线性系统的全状态约束问题,文献[16]进一步研究了一类随机非线性系统的全状态约束问题,文献[3]则研究了一类具有全状态约束和未知扰动的多智能体一致性跟踪问题.此外,系统在保证稳定运行的同时,通常还会对收敛速率,最大超调量,稳态误差等性能指标提出要求.因此,在控制器的设计过程中结合指定性能具有重要意义[17−21].
基于以上讨论,本文针对一类具有全状态约束的非严格反馈多智能体系统一致性跟踪控制问题进行了研究,改进了控制算法.与现有结果相比,本文的优势在于考虑了指定性能,对跟踪误差进行了指定性能变换,从而获得了更小的稳态误差.此外,在控制器设计过程中加入了固定阈值的事件触发机制,设计了一个基于事件触发的自适应控制算法,降低了智能体之间的通讯成本以及控制成本.在控制算法的设计过程中,用径向基函数神经网络(Radial basis function neural networks,RBF NNs)对系统中的未知非线性函数进行处理,从而解决了控制器设计中不满足匹配条件和未知非线性函数的问题.除此之外,在反步法中引入动态面技术,有效地避免了传统反步法中“计算爆炸”的问题.
1 预备知识与问题描述
1.1 代数图论
本文用图论来描述智能体之间的通信拓扑.智能体之间的有向图记为ζ=(V,E,A),其中,V=(1,2,···,N)是节点数,表示系统中含有N个智能体.E ⊆V×V为节点的边,A=[ai,j]∈RN×N为邻接矩阵.节点j到i的边记为(Vj,Vi)∈E,表示智能体i能够接收到智能体j的信息,智能体i的邻居节点的集合定义为Ni={Vj|(Vj,Vi)∈E,i≠j}.对于邻接矩阵A,如果节点j的信息能被节点i接收到,那么ai,j >0,否则ai,j=0.定义节点i的度为对角矩阵D=diag{d1,d2,···,dN}.有向图ζ的拉普拉斯矩阵为L=D −A.定义拓展图其中=(0,1,2,···,N),0 表示领导者,同样的,当节点i能够接收领导者0 的信号时ai,0>0,否则ai,0<0.
引理1[22].如果存在一条路径能够从根节点到达所有其他节点,那么称有向图ζ具有一个生成树.定义B=diag{a1,0,···,aN,0},其中节点0 称为生成树的根,则矩阵L+B是非奇异的.
1.2 系统描述
对于具有N个同构智能体的多智能体系统,第i个智能体可以用以下n阶非严格反馈的非线性系统描述

其中,xi=[xi,1,xi,2,···,xi,n]T∈Rn表示第i个智能体的状态向量,yi ∈R 和ui ∈R 分别表示第i个智能体的输出和控制器输入,fi,m(xi)和fi,n(xi)是未知光滑的非线性函数,i=1,2,···,N.
假设1[1].有向图ζ具有一个生成树.节点0 的期望轨迹yd是一个虚拟的领导者,且只能被部分智能体直接获取.yd已知,yd及其n阶导数都是连续且有界的.
定义1[23].如果对于任意一个先验紧集Ω∈Rn,x(0)∈Ω,存在有界的ε >0 以及常数N(ε,x(0)),使得

则系统(1)的解是半全局一致最终有界的.
1.3 径向基函数神经网络
在本文中,RBF NNs 用于逼近系统中的非线性函数[24−25]
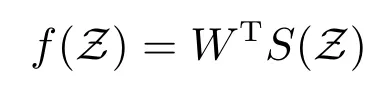
其中,S(Z)=[S1(Z),S2(Z),···,Sk(Z)]T表示基函数向量,k为RBF NNs 的节点数,W=[W1,W2,···,Wk]T∈Rk为权重向量.存在一个恒定的理想权重向量W∗,使以下方程成立
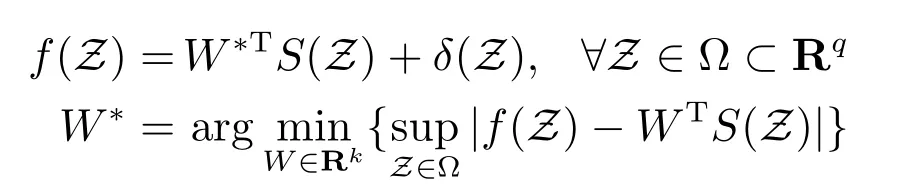

其中,ιi=[ιi1,ιi2,···,ιiq]T和ωi(i=1,2,···,k),分别表示高斯函数的中心和宽度.
引理2[26].令

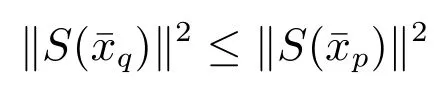
2 事件触发自适应控制算法设计
本文使用反步法和动态面技术设计了一个事件触发自适应控制算法使多智能体系统达到以下控制目标:1)所有智能体的输出都能对期望轨迹进行跟踪并满足指定性能;2)系统中所有的信号都是半全局一致最终有界的.
定义以下坐标变换

指定性能可以用以下不等式进行描述:

其中,δmin和δmax是可调节的参数,性能函数µ(t)有界且严格单调递减,其形式为µ(t)=(µ0−µ∞)e−vt+µ∞,式中,v,µ0和µ∞都是正实数,µ0=µ(0),选取适当的µ0,使得µ0>µ∞,
为了满足指定性能,进行如下等效变换:


其导数为

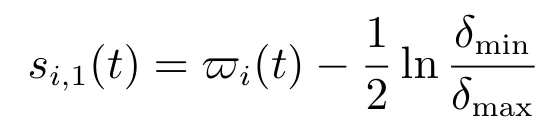
其导数为

定义自适应参数为

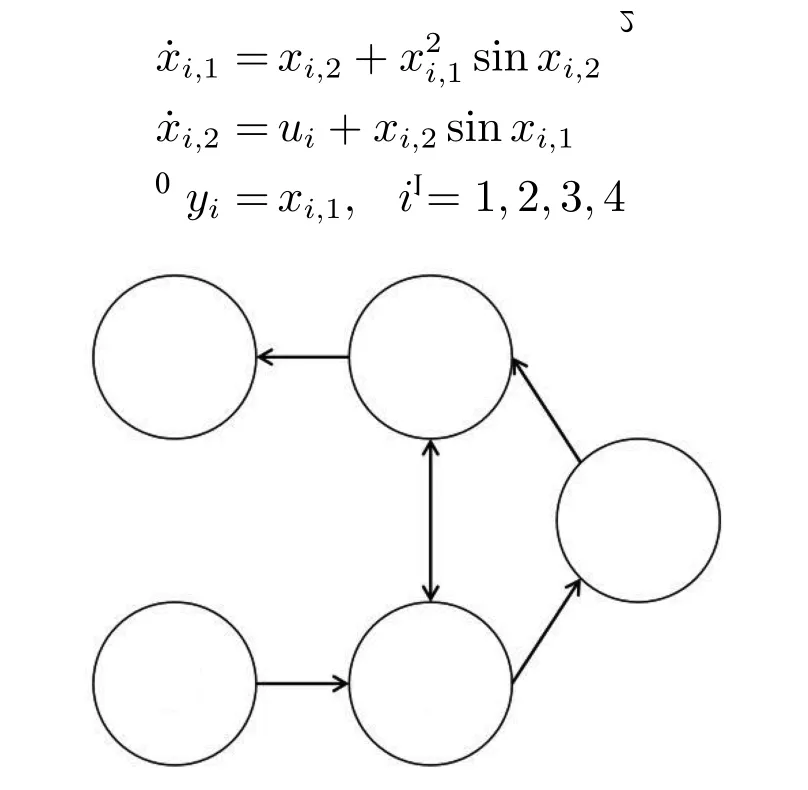
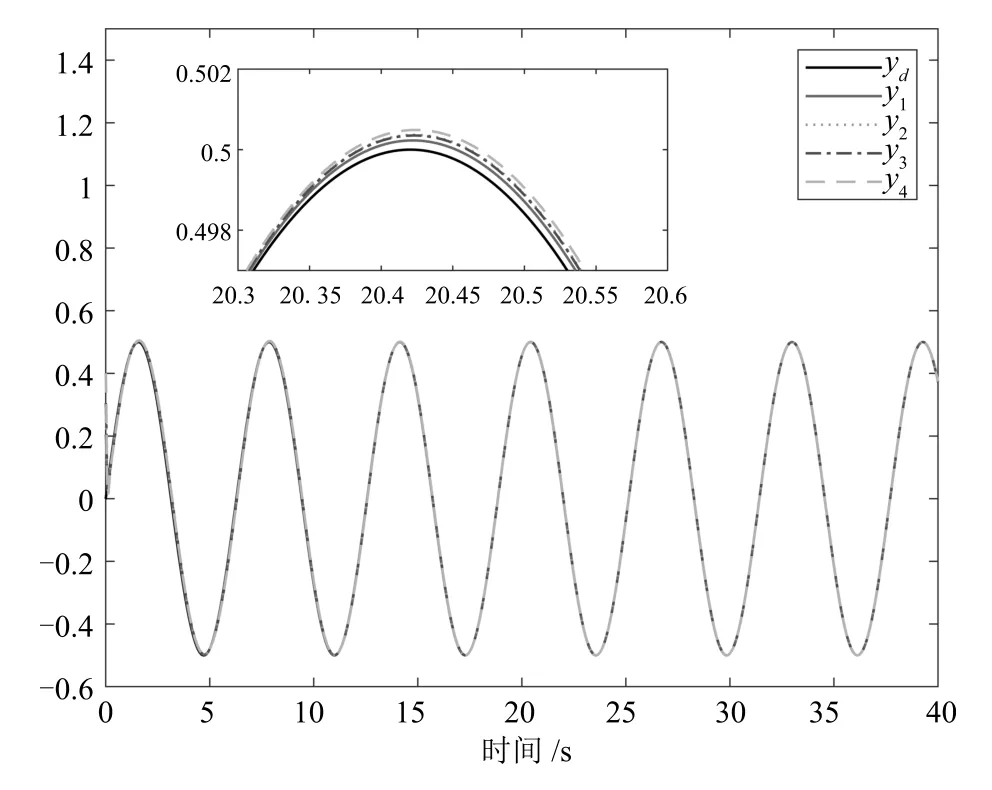
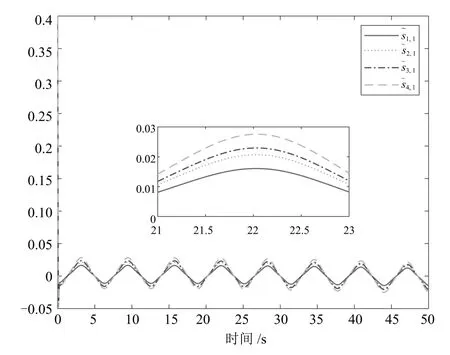
定义kbl为误差si,l的约束,即|si,l| 引理3[27].对于任意正常数kbl,若满足不等式|si,l| 引理4[4].定义s1=[s1,1,s2,1,···,sN,1]T,y=[y1,y2,···,yN]T,=[yd,yd,···,yd]T,其中,yd的个数为N.则有 引理5(Young′s 不等式)[26].对于∀(x,y)∈Rn,有以下不等式成立 其中,p>0,a>1,b>1,(a −1)(b −1)=1. 事件触发自适应控制算法的具体设计步骤如下: 步骤1.反步法第1 步选取的Barrier Lyapunov 函数为 由式(1)∼(4),可得 其中,Zi,1=[xi,xj]T,δ(Zi,1)为逼近误差且|δ(Zi,1)|≤ 由引理2 和引理5,可得 设计反步法第1 步的虚拟控制信号αi,1和自适应律分别为 其中,pi,1,ci,1,σi,1都是正的设计参数. 将式(6)∼(9)代入式(5),可得 步骤2.基于动态面技术[28],定义如下一阶滤波器用于解决反步法的“计算爆炸”问题 其中,τi,2是正的设计参数,由λi,2=zi,2−αi,1可得则有 注1.由步骤1 推导出αi,1后,在下一步的虚拟控制信号设计过程中必须对其求导,并且在之后的每一步中都要对虚拟控制信号进行反复求导,从而产生“计算爆炸”问题.引入动态面技术将虚拟控制信号通过一阶低通滤波器得到其估计值zi,2,在下一步设计过程中用估计值代替虚拟控制信号可以避免对其进行求导,简化了控制器结构. 选取第m(m=2,3,···,n −1)步的Barrier Lyapunov 函数为 由式(1),(2),(11),可得 由引理2 和引理5,可得 设计第m步的虚拟控制信号αi,m和自适应律分别为 其中,pi,m,ci,m,σi,m都是正的设计参数.基于递归的思想,将式(10),(13)∼(16)代入式(12),可得 步骤3.与步骤2 相同,定义滤波器 其中,τi,m+1是正的设计参数,由λi,m+1=zi,m+1−αi,m,可得则有 选取第n步的Barrier Lyapunov 函数为 则Vi,n的导数为 由引理5 可得 自适应控制器设计为如下形式 事件触发机制定义为如下形式 其中,ei(t)=wi(t)−ui(t)表示测量误差,pi,n,ci,n,σi,n,ϵi,mi以及都是正的设计参数,且mi <事件触发时刻定义为tk,k ∈Z+.即当式(22)条件被触发时,控制信号将更新为ui(tk+1),当t ∈[tk,tk+1)时,控制信号为wi(tk)保持不变.于是存在一个连续的时变常数ς(t),满足ς(tk)=0,ς(tk+1)=±1,|ς(t)|≤1,∀t ∈[tk,tk+1),使得wi(t)=ui(t)+ς(t)mi.参考文献[14]可得 由引理5 可得 由引理3 可得 其中, 定理1.在假设1 成立的条件下,考虑虚拟控制信号(8),(15),(19),自适应律(9),(16),(20)及事件触发自适应控制器(18),(21),(22),能够保证式(1)所描述的多智能体系统满足以下条件:1)系统中所有的信号都是半全局一致最终有界的;2)跟踪误差收敛于原点的有界邻域内且满足指定性能.此外,事件触发的时间间隔{tk+1−tk}存在一个下界t∗,t∗>0.即该事件触发自适应控制器不会发生奇诺现象. 证明.Lyapunov 函数定义为 由式(27)可得其导数为 则式(28)可以写为 则所有的信号都是半全局一致最终有界的,由式(29),得基于引理4,可得 由式(30)可知,通过选择合适的设计参数可以使跟踪误差收敛于以原点为中心的有界邻域内. 由ei(t)=wi(t)−ui(t),∀t ∈[tk,tk+1),可得 考虑有向拓扑图下由4 个跟随者和1 个虚拟领导者组成的多智能体系统,如图1 所示.其中第i个子系统的动态模型为 图1 通信拓扑图Fig.1 Communication topology 作为虚拟领导者的期望轨迹为yd=0.5 sint.设计的性能函数为µ(t)=0.97e−0.3t+0.03.数值仿真程序中设计参数的值分别设置为ci,1=ci,2=80,σi,1=σi,2=0.001,pi,1=pi,2=10,τi,2=0.02,δmin=0.999,δmax=1,kb1=kb2=2,=8,mi=0.6,ϵi=1.5.初始值设置为:xi,1(0)=[0.2,0.3,0.3,0.4],xi,2(0)=[1.0,−1.5,1.2,−0.6],=0,zi,2(0)=0.1. 图2 参考信号yd 和输出信号yiFig.2 Reference signal yd and output yi 图3 具有指定性能的跟踪误差Fig.3 Tracking errors with prescribed performance 图4 不具有指定性能的跟踪误差Fig.4 Tracking errors without prescribed performance 图5 控制信号uiFig.5 Control signal ui 图6 u1, u2的事件触发时间间隔Fig.6 Time interval of event-triggered for u1, u2 图7 u3, u4的事件触发时间间隔Fig.7 Time interval of event-triggered for u3, u4 图2∼7 为仿真结果,图2 表示虚拟领导者的期望轨迹yd和每个跟随者的输出信号yi的响应曲线,由图可以看出各跟随者在较短的时间内实现了对期望轨迹的跟踪,表明本文提出的控制算法快速实现了多智能体的一致性跟踪.图3 和图4 分别表示具有指定性能的跟踪误差和不具有指定性能的跟踪误差,虽然跟踪误差均能快速收敛于以原点为中心的有界邻域内,但通过对比可得,在不具有指定性能的条件下,稳态误差接近0.03,而具有指定性能时稳态误差小于0.003,因此通过指定性能变换可以显著减小多智能体一致性跟踪控制的稳态误差.控制器输入ui由图5 表示,控制器输入的数值除了在起始阶段的瞬间有较大的波动,在其余时间均小于7,表明该控制器性能良好,能耗较低.图6 和图7 是ui的事件触发时间间隔和事件触发次数,横坐标为事件触发时间,纵坐标为事件触发的时间间隔.控制器u1,u2,u3,u4在40 s 内的事件触发次数分别为1 400,399,1 055,386,表明事件触发控制器具有减少控制信号更新次数和降低控制成本的优点,且没有发生奇诺现象. 本文研究了一类具有全状态约束的非严格反馈多智能体一致性跟踪问题.在控制算法设计过程中考虑了指定性能,获得了期望的稳态误差.此外,还设计了一个固定阈值的事件触发机制,降低了智能体之间的通讯成本和计算压力.本文给出了控制算法的详细推导过程和稳定性证明过程.最后通过仿真结果验证了本文所设计的控制算法的有效性.在未来的研究中,我们将考虑更为复杂的应用环境,提高多智能体系统的抗干扰能力.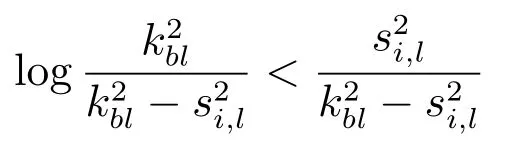


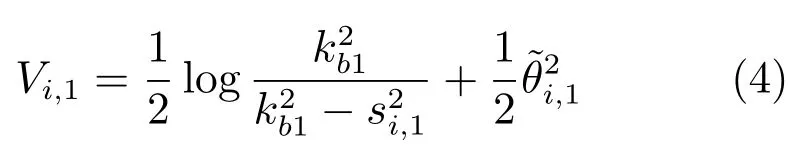



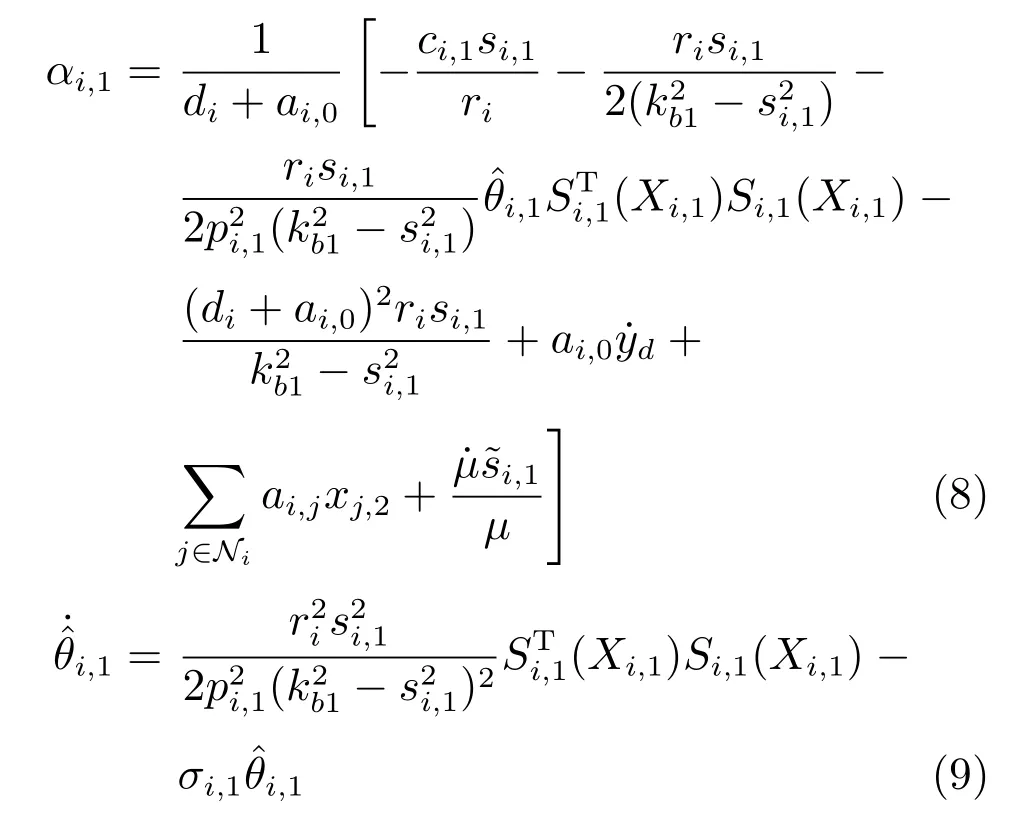
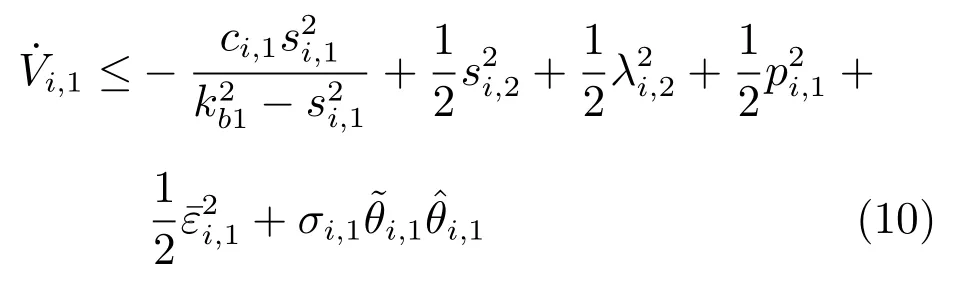



















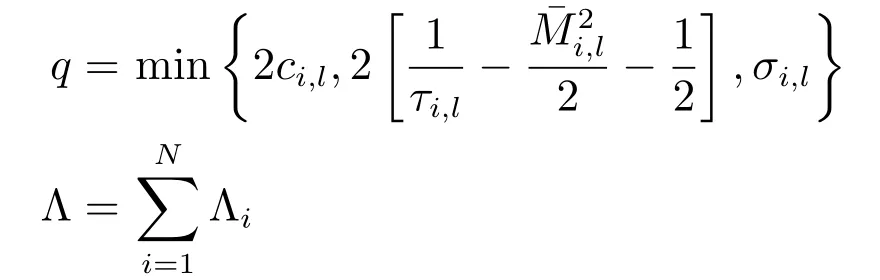




3 仿真实例




4 结论

