基于可穿戴式惯性传感器的人体运动跟踪方法综述
张鋆豪 何百岳 杨旭升 张文安
人体运动跟踪是一种利用传感器来测量人体在三维空间运动时运动参数的技术,早在第二次世界大战之后,斯坦福大学就提出了人体运动捕捉这一概念,当时主要用在医疗康复领域,用于对伤残、截肢病人的运动分析和治疗.近年来,人体运动跟踪技术的发展促使该技术广泛应用于医疗、体育、人机交互、虚拟现实和影视制作等领域.
常见的人体运动跟踪系统主要有机械式的、光学式的、声学式的和电磁式的,这些人体运动跟踪技术已渐渐不能满足目前人体运动跟踪系统的要求,其中机械式的人体运动跟踪系统容易使人体运动受限,基于光学的人体运动跟踪系统较为昂贵、对光照环境要求高、易受遮挡,基于声学的人体运动跟踪系统实时性比较差、易受干扰,基于电磁的人体运动跟踪系统易受磁场干扰,场地周围的金属物品会造成磁场畸变,严重影响精度.人体运动跟踪技术中最大的挑战是使用非介入式的传感器和在不受限的环境中准确估计人体的运动姿态.随着微机电系统(Micro-electro-mechanical system,MEMS)技术的发展,基于可穿戴式惯性传感器的人体运动跟踪技术逐渐受到人们的关注,惯性式人体运动跟踪系统具有佩戴方便、运动空间不受限和成本低等优点.
上世纪90 年代末,国外的Luinge 等[1]、Bachmann 等[2−3]和Yun 等[4]已开展了对基于可穿戴式惯性传感器的人体运动跟踪技术的研究,EI-Gohary 等[5]首次将上肢五自由度运动学模型引入到上肢关节角度估计中.在商业领域,目前主要有美国的Innalabs、荷兰的Xsens 等几家公司在出售基于惯性传感器的人体运动捕捉系统.国内的相关研究起步较晚,目前主要有中国科学院自动化研究所吴健康等[6−10]、浙江大学金李启雷等[11−13]、哈尔滨工程大学王科俊等[14−16]和大连理工大学王哲龙等[17−19].吴健康等[6−10]研制的MMocap 动作捕捉系统,由16 个惯性传感器(包括加速度计、陀螺仪、磁力计)节点和一个主控原件组成,数据通过蓝牙装置传到计算机中,是国内第一个实现商业化的惯性运动捕捉系统.目前国内开发惯性动捕系统比较成功的是北京诺亦腾科技有限公司,戴若犁带领的团队成功研发了以Noitom 为品牌的全身动作捕捉系统.
随着对基于可穿戴式惯性传感器的人体运动跟踪研究的深入,大量的成果不断涌现,众多学者逐渐展开了对惯性式人体运动跟踪的综述工作,对该领域进行归纳与总结.在已有的综述文献中,部分只是面向具体应用进行展开,例如文献[20]介绍了穿戴式惯性传感器在步态分析、跌倒检测和睡眠质量监测方面的应用,文献[21−22]介绍了人的室内惯性定位系统,文献[23]对基于惯性传感器的行人步行速度估计展开了综述,文献[24]综述了穿戴式惯性传感器在体育训练领域的一些应用.当然,也有一些学者对惯性式人体运动跟踪技术进行了较为全面的阐述、分析与整理.文献[25]着眼于基于惯性传感器的上肢运动跟踪,从方法和应用两个方面进行了详细的综述,文献[26]从穿戴式体感网技术和数据融合方法两个角度出发讨论了如何提高基于惯性传感器的人体位姿估计精度,文献[27]对惯性式人体运动跟踪技术进行了综述.调研发现,现有的综述文章对文献的阐述还不够全面,对传感器初始对准、模型不确定性、传感器误差等关键问题也缺乏完整的梳理,且目前国内未见有文献评述这方面的研究进展,
基于惯性传感器的人体运动跟踪系统如图1 所示,为了较为全面地阐述和整理相关文献,本文重点从以下几点展开综述:1)归纳当前人体运动学模型和生物学约束;2)强调传感器初始对准的重要性,并对传感器初始对准方法进行总结;3)对传感器误差处理和数据融合方法进行详细整理;4)概述相关方法应用于实际的现状.最后,总结当前研究及应用中存在的亟待突破的关键问题,为后续研究提供借鉴.
1 人体运动学建模及约束
人体模型是对人体进行抽象处理得到的一种对人体形态的近似描述,基于惯性传感器的人体运动跟踪系统,利用传感器采集的人体动作数据,对建立的人体运动学模型进行驱动,从而可对人体运动姿态进行近似跟踪,因此,建立一个符合人体行为特征的三维人体模型,以及选用合适的运动学表示方法,对于形象逼真地跟踪人体运动显得尤为重要.本节首先描述肢体运动的运动学表示方法,然后介绍常用的人体运动学模型,最后说明人体的生物学约束.
1.1 运动学表示方法
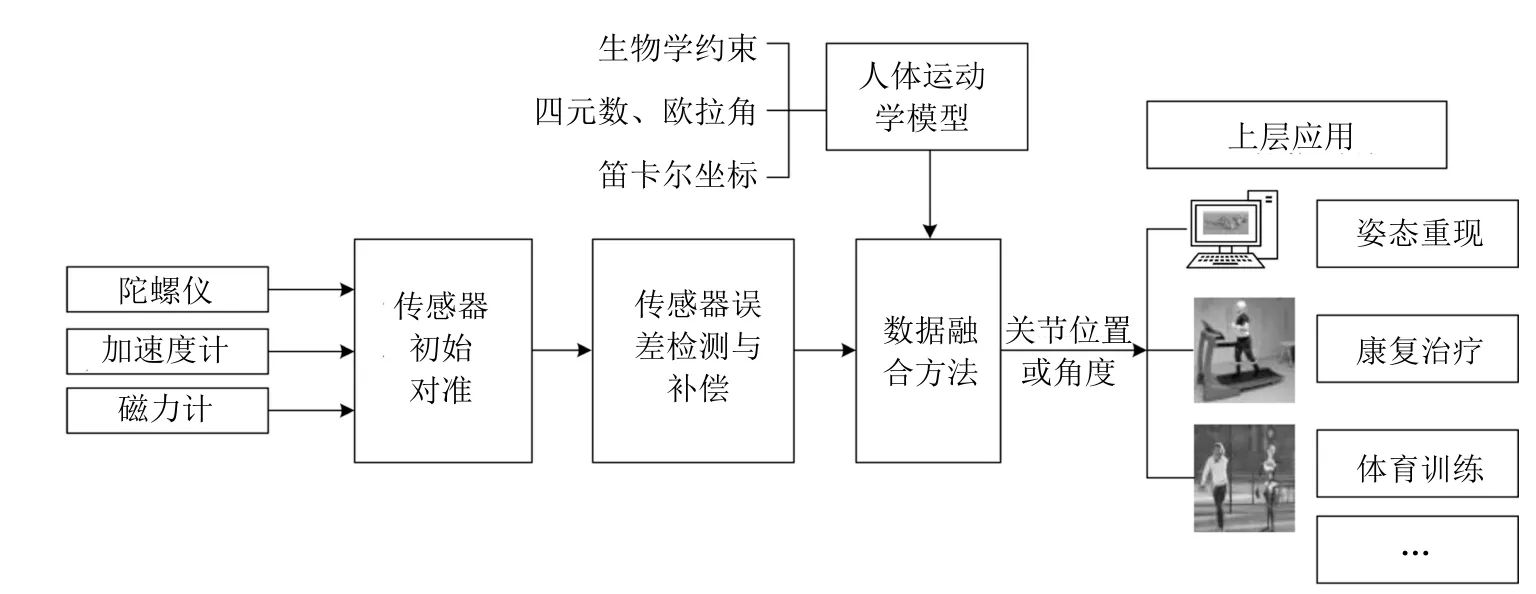
图1 基于惯性传感器的人体运动跟踪系统示意图Fig.1 Diagram of human motion tracking system based on inertial sensors
为了便于研究人体的运动,大部分关于人体运动跟踪的文章将人体简化为多刚体系统.人体运动姿态在三维空间上存在6 个自由度,包括各个肢体部位的位置和方向.在基于惯性传感器的人体运动跟踪中,通常会定义三种坐标系:传感器坐标系,肢体坐标系和参考坐标系.人体运动跟踪的目标是获得肢体坐标系相对于参考坐标系的位姿.姿态描述的方法有很多,其中包括欧拉角、四元数等.欧拉角能够形象地描述人体关节运动,因此被广泛用于人体姿态估计中.欧拉角是用来确定定点转动刚体位置的一组独立的角参量,欧拉角使用偏航角,俯仰角和翻滚角来描述刚体绕各坐标轴的旋转角度.特别地,在人体姿态估计中,人体可以分为矢状面、冠状面和横断面三个基本平面.矢状面沿着身体的前后方向对称地把身体分为左右两部分,俯仰角定义为姿态在矢状面内的变化角度;冠状面是指沿身体左右径所作的纵切面,翻滚角定义为姿态在冠状面内的变化角度;横断面是指与大地平行的身体横切面,偏航角定义为姿态在横断面的变化角度.然而,在使用欧拉角描述旋转运动时,会存在万向节死锁的问题[28],可使用四元数代替欧拉角,四元数表示方法可提高算法的可靠性,避免出现万向节死锁问题[2,29−31],在需要建立连续的运动轨迹时,四元数方法更容易进行插值[8].文献[32−33]对四元数法进行改进,使用了参数四元数法,将四元数分解在更方便计算人体生物学约束的实际关节轴上.除了四元数法之外,双欧法[34−36]通过建立正反两个欧拉方程来描述刚体旋转,利用正、反欧拉角解算精华区和奇异点的倒挂关系,在二者解算的精华区进行交替计算,将精华区覆盖了姿态角全域,能够消除单一欧拉角方法的奇异性问题.
1.2 人体运动学模型
在对人体姿态进行跟踪时,通常需要建立相应的三维连接关系来辅助跟踪,本文按照文献对关节连接方式的不同,将描述人体运动学的模型分成三类.第一类方法对关节连接不作限制,独立估计各个部位的姿态.此类方法假设传感器拥有很高的精度,能够单独估计每个身体部位的姿态[37−38].文献[39]使用这类方法分别估计出各个部位的位姿,再引入生理学约束防止姿态的估计值超出人体实际的运动范围.
第二类方法认为关节是紧耦合的,即人体的运动链模型[8],如图2(a)所示.该模型把人体各肢体部位假设成用铰链连接的刚体,每相邻两个部位之间的自由度根据人体关节的旋转自由度而定,例如肘部关节为一个2 自由度的铰链关节,肩关节为3自由度的球窝关节[8,40−41].
上肢由上臂、前臂和手三部分组成,可根据实际应用场景的需要建成具有不同自由度的模型.其中,使用最为广泛的是7 自由度模型,7 自由度模型分为两类,第一类对应肩关节的旋内/旋外、内收/外展和屈/伸3 个运动自由度,肘关节的旋内/旋外和屈/伸两个自由度,以及腕关节的内收/外展和屈/伸2 个自由度[42−44].第二类除了考虑肩关节的3 个自由度和肘关节的2 个自由度外,还考虑了肩胛骨相对运动的2 个自由度,分别通过放置在肩膀、上臂和前臂上的3 个传感器来测量这3 个关节的运动[45].另外,根据实际应用场合的需要,一些文献采用了5 自由度和4 自由度的人体上肢模型.5 自由度模型一般在第一类7 自由度模型的基础上省略了腕关节的2个自由度,只考虑上臂和前臂的运动,因其结构简单又不失一般性,因而被很多学者采用[5−6].Ruffaldi等[46]将概论图模型引入上肢5 自由度模型中.在一些特殊的应用场合,文献[47]针对中风病人的康复治疗,只考虑患者肩关节3 个自由度的运动和肘部的屈/伸运动,因此使用4 自由度模型即可.文献[48]研究了上臂和躯干的相对运动,简单的4 自由度模型就能满足要求.若进一步考虑上肢关节的复杂运动,还可以采用具有更多自由度的模型,华中科技大学陈文斌[49]通过从上肢肩关节复合体和肘关节复合体中抽取出等价运动链,建立了具有4 个关节和11 个自由度的人体上肢运动链模型,11 个自由度为胸锁关节内收/外展、抬起/下落和轴向转动3 个自由度,肩锁关节内收/外展、侧旋/回旋和前倾/后倾3 个自由度,盂肱关节内旋/外旋、外展/内收和前屈/后伸3 个自由度,肘关节屈/伸和旋前/旋后2 个自由度.

图2 运动链模型和自由部位模型示意图Fig.2 Diagram of kinematic chain model and free segments model
人体的下肢由大腿、小腿和脚三个部位构成,大腿通过髋关节和骨盆相连.文献[50]建立的下肢模型以运动链模型的形式将各个部位连接起来,它含有髋关节,膝关节,踝关节,脚趾共4 个球关节,有12 个自由度.Joukov 等[51],使用了简化后的4 自由度下肢模型,其中髋关节是存在3 个自由度的球窝关节,另外,它根据生物学约束,膝关节仅保留弯曲/伸展自由度.基于运动链的下肢模型常用于人的步行轨迹跟踪.文献[52]直接对步行速度积分到步长,最后还原行走轨迹.文献[53]还进一步检测出步行方向和每一步的时长,提高了跟踪的准确率.文献[54]为了解决室内磁干扰较强的情况,通过UWB和运动链模型共同确定航向角,该方法能够保证系统有较强的鲁棒性,甚至能够适应跑步和跳跃的场景.文献[17]还通过运动链模型和零速度更新算法结合,提高了行走轨迹的跟踪精度.在医疗康复领域,Cutti 等[55]提出的outwalk 协议可用于对脑瘫小孩和截肢患者的步态分析.
全身的人体模型一般建成树状结构,如图3 所示身体部位的移动可以看成是子节点相对于父节点的运动,父节点的姿态信息能够通过运动链模型传递给它的子节点.文献[8,56−58]采用的方法都是选择某一关节作为全身运动的根节点,从根节点递推计算出每个子节点的位姿信息.其中,文献[8]定义连接髋骨和胸腔骨骼的连接点作为整个人体树状结构的根节点,文献[56]提出用优化的方法重建模型,选取骨盆作为根节点进行全身姿态重建,结果表明,选取骨盆做根节点时计算效率较高.
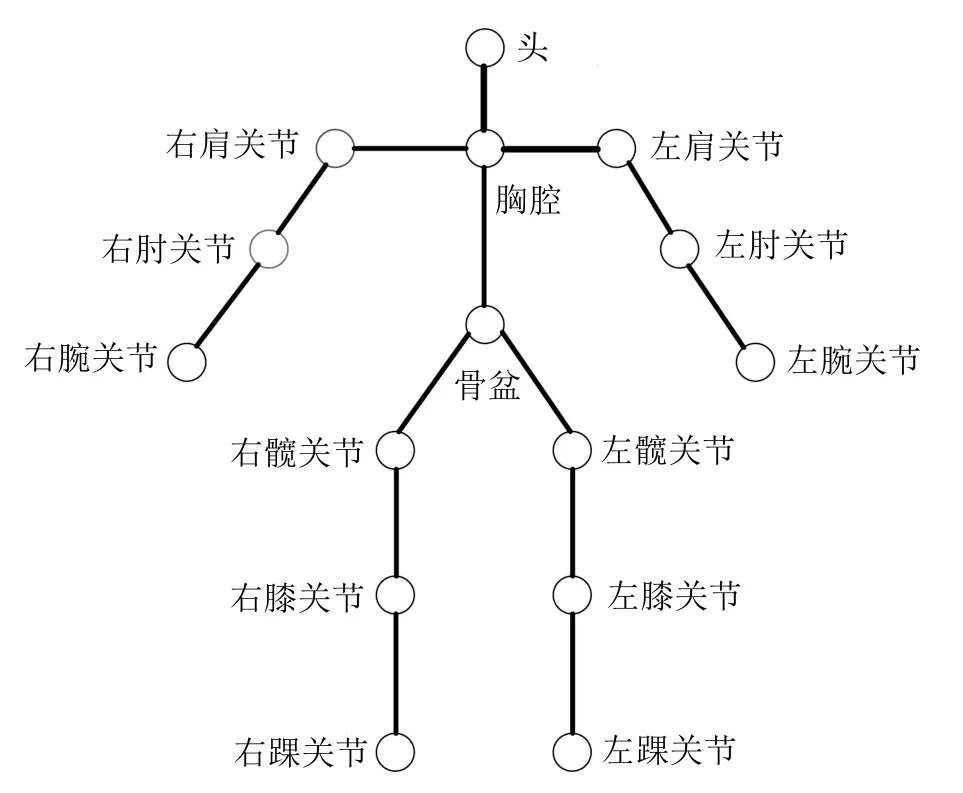
图3 人体树状结构图Fig.3 Diagram of human tree structure model
与人体实际结构相比,运动链模型也存在一些不足,在实际情况中有些关节并不是完美的铰接关节,每个关节在运动时会产生一些相对的位移,因此一些文献提出了自由部位模型[59−60],如图2(b)所示.以肘关节为例,当尺骨相对于肱骨移动时,其轴线不固定[61],建立肘部模型时,难以准确定位旋转轴的真实方向[62],因此肘关节并不是一个完美的铰链关节,选用自由部位模型进行建模更为合适.
1.3 人体生物学约束
运动链模型是人体运动跟踪中最常用的模型,它通过关节将身体相邻部位紧密连接,每个关节最多可以拥有3 个自由度.但是对于手肘和膝盖等关节,在某些轴上的运动自由度存在限制,在进行人体姿态估计时应该考虑这类关节约束.对于这一类问题,国内外学者进行了一系列研究.对上肢关节自由度约束的研究主要集中于肘部,Zhang 等[7,63]根据肘关节内收/外展的范围极小这一事实提出了分层滤波算法,在第二层中通过肘关节约束建立的滤波算法提高姿态估计的精度.同样,Luinge 等[64]在仅使用陀螺仪和加速度计的情况下,以肘部内收/外展角度为零作为约束建立优化问题,通过最小二乘法求解该优化问题来提高姿态估计的精度.EIGohary 等[5]和Zhang 等[6]在运动链模型中引入对肘关节自由度的限制,从本质上解决了上肢运动估计时肘关节内收/外展角错误估计的问题.同样地,对下肢关节自由度约束的研究主要集中于膝关节,膝关节与肘关节类似.Cooper 等[65]仅考虑膝关节的屈/伸自由度,通过绑在大腿和小腿上的惯性传感器有效估计膝关节角度.Meng 等[66]同样将膝盖约束成仅具有屈/伸自由度的关节,因此表示膝关节屈/伸运动的四元数向量应该与膝关节的内收/外展关节轴和内旋/外旋关节轴均正交,以此为约束可减小线性加速度和磁力计扰动的影响.
除关节自由度约束外,每个关节的运动范围也存在一定的限制.文献[32]提到在仅使用加速度计测量肘关节角度时,会存在歧义解,通过引入关节运动范围的约束,可以解决姿态解算结果的模糊性问题.另外,考虑每个关节的角度约束后,可采用带有角度约束的数据融合方法估计人体运动姿态,El-Gohary 等[5]将关节角度的约束作为状态约束,采用带有状态约束的无迹卡尔曼滤波器(Unscented Kalman filter,UKF)估计上肢运动姿态.文献[67]总结了带有状态约束的卡尔曼滤波方法.
另外,一些文章还进一步考虑了关节位置和速度等约束.文献[68]为了提高上肢姿态估计的精度,引入以下约束:由上臂和下臂传感器分别计算所得的肘关节的运动速度应该相等.文献[50]在估计人步行时的全局位移时,为了减小累积误差,考虑以下约束:分别由左下肢和右下肢传感器独立估计得到的人体位移应该尽可能相等,基于此约束的融合方法将在第3.3.2 节具体阐述.
2 传感器初始对准
本节介绍传感器初始对准方法,用于解决传感器安装姿态与理想姿态不一致带来的问题.在实际中,往往存在传感器的敏感轴与待测部位轴向不一致的现象,即无法将传感器模块安放在理想的位置,如图4 所示.因此无法直接得到肢体坐标系相对于参考坐标系的姿态,而且每次测量也不能保证安装位置的一致性.还有一种情况是使用多个传感器进行姿态测量时,每个传感器的基准坐标系和初始姿态都是不同的.传感器的安放误差以及多个传感器之间的不对准误差都会严重影响到多传感器数据融合算法的有效性,因此初始时刻必须进行传感器的对准.向量在加速度计和磁力计的各轴分量计算出初始翻滚角、俯仰角和偏航角,进而求出初始对准的坐标系变换矩阵,然后基于参考向量修正坐标系变换矩阵分别完成对3 个欧拉角的补偿,得到精确的人体下肢初始姿态信息.
动态对准方法要求被测试者完成一种或一组动态动作,例如关节的内收/外展、关节内旋/外旋和屈/伸等动作.Luinge 等[64]设计了2 种动作,用来完成前臂和上臂传感器的初始对准.对准前臂传感器时,需让上臂保持垂直,前臂抬起,绕桡骨左右各旋转180◦;对准上臂传感器时,第1 步将肘部放在水平桌面上绕肱骨做旋转运动,第2 步将前臂抬起至水平,保持前臂不动,上臂做外展运动,对准过程中用到了陀螺仪和加速度计.在文献[64]的基础上,Yang 等[72]定义了4 种对准动作,并在对准过程中采用扩展卡尔曼滤波器(Extended Kalman filter,EKF)消除动态对准动作中线性加速度的影响.此外,文献[73−76]也设计了相应的动态对准方法.以上的几种动态对准方法,均要求被测试者完成特定的对准动作,且这些动作对关节的运动角度有要求,例如文献[72]中要求前臂绕桡骨分别内旋/外旋180◦.
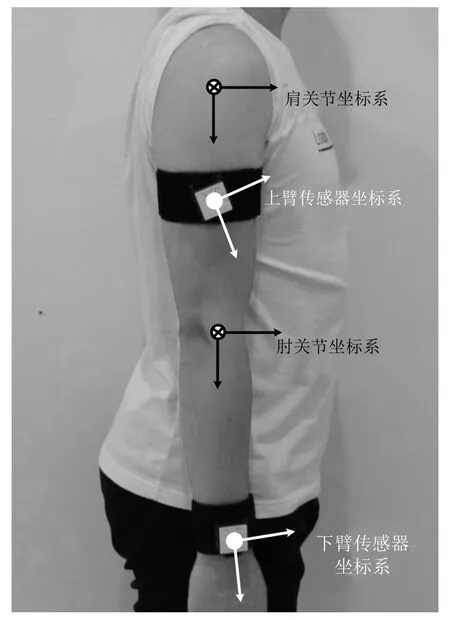
图4 传感器初始不对准误差示意图Fig.4 Diagram of initial sensor miscalibration error
文献[65]进行传感器初始对准时,通过在下肢关节处安放标记点,借助外部相机完成对准过程,文献[69]通过自行设计的测量设备完成对准过程.除此之外,通常要求被测试者完成一些规定的动作以完成传感器的初始对准,分为静态对准方法和动态对准方法.
在上肢传感器的初始对准中,最常见的两种静止对准姿势是N-pose(手臂自然向下垂直于地面)[6,44]和T-pose(手臂平举平行于地面,手掌向下)[70−71],静止对准姿势示意图如图5 所示.文献[6,44]在初始时刻让被测试者保持N-pose 姿势静止5 s,通过采集到的加速度计和磁力计信号得到初始对准的坐标系变换矩阵.文献[70]在对准过程中结合了N-pose 和T-pose 两种姿势以更精确地得到初始对准结果.在下肢传感器初始对准中,通常让人体保持静止站立的姿势,文献[66]通过陀螺仪和加速度计的测量值完成被测试者静止站立阶段的初始对准.文献[17−18]采用的方法是在步行开始前的静止站立阶段,通过重力向量和地磁矢量两个参考
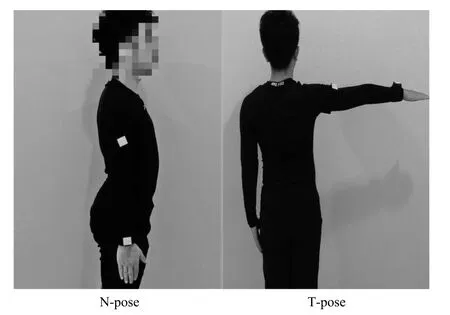
图5 上肢静止对准动作示意图Fig.5 Diagram of upper limb static calibration
静态对准方法操作方便,但是对被测试者来说,要完成完全标准的N-pose 或T-pose 动作并非易事,往往需要借助外部设备或专业人士的帮助才能使手臂或下肢完全保持垂直或水平.采用动态对准方法时,即使是健康的人也无法标准地完成每个动态对准动作,对于一些失去部分行动能力的病患尤甚.这类传感器对准方法的精度完全依赖于被测试者完成相应对准动作的精度,文献[60]表明基于EKF 融合算法的人体姿态估计结果对初始对准误差较为敏感,若初始对准时存在误差,人体姿态估计精度会明显下降.因此,近年来一些学者提出了同时姿态估计和在线对准的方法[77]和无需对准的人体姿态估计方法[78−79].文献[77]将同时在线估计上肢关节角度四元数和位置以及传感器对准参数的问题,建模成一个带有约束的最小二乘问题,通过滑动窗的方法求解最优的参数.文献[78]提到由于肘部只有2 个自由度,当测量肘部弯曲角度时,可将肘部的旋转运动分解到这2 个旋转主轴上,因此可避免传感器坐标系的初始对准,借助任意非正交旋转轴的欧拉角解算方法得到肘部的弯曲角度.文献[79]提出的无校准方法无需佩戴者完成特定的对准动作,上肢运动的姿态估计结果不易受到传感器安装位置的影响.
3 传感器信号处理
在完成传感器的初始对准后,需对来自各个传感器的数据进行处理和融合以精确地估计人体的姿态.人体的运动跟踪涉及陀螺仪、加速度计和磁力计,陀螺仪动态精度较好,但陀螺仪最显著的缺点是容易受到随机漂移的影响,加速度计和磁力计在静态时测量精度较高,但加速度计在动态运动中存在线性加速度的干扰,室内环境中磁力计容易受到铁磁扰动.因此,要想准确地获得人体位姿估计的结果,在对传感器信号进行处理时,必须解决两个关键问题:1)对传感器的误差进行补偿和校正;2)采用合适的算法融合各传感器数据.
3.1 传感器种类
在处理传感器误差和采用融合算法之前,必须了解各类传感器的特性.陀螺仪可以测量高速转动下的转动角速度,拥有良好的动态响应性,但是自身也有缺点,随着时间的累积,对转动的角速度进行积分就会产生累积误差,发生漂移.加速度计可以测量载体在三轴方向上的加速度,在静态或匀速状态下,可以通过重力加速度在三轴上的分量准确求得俯仰角和翻滚角.三轴磁力计通过感应当地的磁场通量来计算载体方位姿态,所在地球磁场恒定不变时,磁力计在静态下有良好的测量特性,不会随时间发生漂移.因此,根据加速度计和磁力计数据解算得到的姿态角可作为参考值对陀螺仪的解算结果进行校正.由于每个传感器都有自己的特性,需要各传感器之间的相互配合才能达到人体姿态跟踪的目的.为了克服惯性传感器和磁力计的缺点,一些文章还结合了UWB[54]、视觉[80−82]、编码器[83]和超声波[84]等其他传感器.
早期最常用的传感器组合是陀螺仪和加速度计,其中Luinge 等[1,64,85]和EI-Gohary 等[5,71,86]均采用陀螺仪和加速度计的组合估计关节运动角度.另外,文献[87−89]同样只采用了陀螺仪和加速度计.由于加速度计的测量值只能用来校正翻滚角和俯仰角,无法校正航向角的误差,文献[64,86]分别通过肘关节自由度约束和零速度更新算法,校正陀螺仪漂移对航向角的影响.三轴磁力计可根据磁场强度测量值确定传感器模块与地磁北极的偏角,因此可用来校正航向角.大部分文章均采用陀螺仪、加速度计和磁力计的组合进行人体位姿估计,其中Bachmann 等[2−3]、Roetenberg 等[90−91]、Yun等[4,92−93]、Zhou 等[47,94−95]、Zhang 等[7,63,96]、Sabatini 等[97−99]和Fourati 等[100−101]的工作较为突出.另外,文献[32,102]仅采用加速度计研究了上肢在矢状面的运动.
惯性传感器面临的最大问题是存在随机漂移,为了进一步提高人体位姿估计的精度,一些文献将不易受到随机漂移干扰的传感器与惯性传感器相结合.文献[80]利用惯性传感器和Kinect 传感器实现机械手遥操作,机械手可模拟人手完成抓取物品和钉钉子等动作.文献[81−82]提出了基于单目视觉和6 轴惯性传感器的上肢位置估计方法.文献[54]介绍了一种将惯性传感器与超宽带(UWB)定位系统相结合的人体运动的三维定位和姿态跟踪算法,UWB 的测量数据可替代磁力计达到校正航向角的目的.文献[83]基于光电编码器和加速度计,设计了能够跟踪手臂运动的传感网系统.文献[84]结合超声波传感器和惯性传感器估计人步行时的相对位置.
3.2 传感器误差
如上所述,陀螺仪信号存在随机漂移,虽然在短时间内直接对陀螺仪信号进行积分能保证输出角度的准确性,但随着时间的增加,输出误差也累积增加,因此不适合单独使用陀螺仪进行姿态计算.加速度计除了存在随机漂移外,还易受线性加速度的影响,磁力计的测量精度易受到磁场干扰的影响.文献[87]比较了九轴IMU 在静态、慢速运动和动态运动下的角度测量精度,实验结果表明,如果不对传感器误差加以补偿,就会引起动态精度的下降.下面从随机漂移、线性加速度干扰和磁力计扰动三部分展开叙述.
1)随机漂移
针对陀螺仪和加速度计的随机漂移,文献[50,64,86]将随机漂移建模成一阶高斯–马尔科夫过程,并利用卡尔曼滤波器进行在线估计,从而可实时补偿该随机漂移.文献[103]在估计肘部和腕部的位置时,对相邻采样时刻的位置变化量人为设定一个上界,可在一定程度上减小随机漂移的累积误差对位置估计的影响,在下肢的位姿估计中,常使用零速度更新算法来消除传感器误差的累积[17−18,50,97],使人体步态参数更准确,将误差累积限制在每一步之内,最大限度地减小误差累积.使用零速度误差补偿的理论依据为:在每一步的开始阶段(起步)和结束阶段(站立),足部速度应为零.由于客观存在的传感器噪声和信号漂移会导致积分误差,使得在每一步的完全站立阶段足部速度不为零,这就需要使用这个非零值对速度进行误差补偿,从而满足客观真实状态,误差补偿最简单的方式是直接将处于完全站立相的足部速度置为零.
2)线性加速度
在跟踪人体运动时,加速度计通常处于动态环境中,当人体运动的加速度相对于重力加速度无法忽略时,此时根据加速度计测量值计算出的俯仰角和横滚角存在较大的误差,如果不对线性加速度计加以补偿,就会引起动态精度的下降.因此,学者们提出了一些线性加速度检测方法[57,63,68,88,104−105],一般将线性加速度扩张成系统的状态变量,通过各种滤波方法进行估计.当检测到线性加速度后,一方面可直接从加速度计的测量值中消除线性加速度分量[57,88],消除线性加速度分量之后,加速度计测量值只剩下重力加速度分量,可直接用于解算俯仰角和翻滚角.另一方面可根据线性加速度的大小自适应调整加速度计量测噪声方差的大小[63,68,104−105].文献[68]根据线性加速度的大小对方差进行二值调整,当线性加速度与重力加速度之差小于设定阈值时,方差为标准设定值,否则设置方差为一个较大的数值,减小当前时刻加速度计的测量值在位姿估计中的权重,可避免线性加速度过大时导致位姿估计结果发生偏移.然而,仅对方差进行二值调整过于简单,在两者之差小于阈值时,线性加速度的噪声方差均设置为同一值不合理,因此,文献[63,104−105]根据线性加速度的大小设计了连续的自适应调整策略.特别地,文献[105]为了提高自适应滤波器的收敛速率,提出了一种基于隐马尔科夫模型的自适应调整策略.
3)磁力计扰动
当周围存在磁场干扰时,特别是在室内环境中,磁力计的测量精度会受到很大的影响.磁场干扰可分为硬铁干扰和软铁干扰.硬铁干扰产生于永久磁铁,这些干扰源的大小及与磁力计的相对位置固定,一般假设不变,可作为零偏处理.文献[106]设计了两步法校准磁力计,消除了磁力计的零偏.软铁干扰来自于磁力计附近的其余磁性材料的影响,软铁干扰一般是时变的扰动.
通常有两种常用的策略用来解决时变磁力扰动的问题:a)基于阈值的方法.基于阈值法判断每个采样时刻的磁力计数据是否可用,如果与阈值相差较远,则舍去该时刻的磁力计测量值或根据磁力计的测量值自适应调整过程噪声的方差.文献[107]采用如下策略自适应调整量测噪声方差阵:如果当前采样时刻的量测值与前一时刻的量测值之间的误差大于一个设定的阈值,则设置相应的方差为一个较大的值,否则保持原来设定的方差值.文献[108]将磁场强度的量测值与参考值进行对比,如果两者差值大于设定的阈值,则舍弃该时刻的量测值,当小于阈值时,则根据差值大小实时调整噪声方差.文献[109]与文献[108]相似,需将当前时刻磁力测量值与设定的阈值对比,当前时刻的磁力计量测值被舍弃时,用一个预测值代替舍弃值作为QUEST 姿态解算算法的输入.b)基于模型的方法.一般将磁力计扰动扩张成系统的状态变量,通过各种滤波方法估计出磁力计扰动,从而可在磁力计测量值中补偿该扰动.文献[90,98]将磁力计扰动建模成一阶马尔科夫过程,分别通过互补卡尔曼滤波器和EKF 估计磁力计扰动,估计结果用来修正由陀螺仪解算得到的角度.文献[99]提出了状态维数可变的EKF 算法,在磁力计扰动较小时,采用一阶马尔科夫过程描述磁力计扰动,当磁力计扰动较大时,采用二阶马尔科夫过程描述磁力计扰动.文献[110]总结了基于卡尔曼滤波的磁力计扰动补偿方法.
3.3 数据融合方法
人体运动跟踪通过对信息的采集、坐标系的变换,得到人体位姿估计的结果.然而,单个传感器由于受到噪声干扰等影响,往往导致姿态跟踪精度较低,因此,多传感器信息融合成为提高姿态跟踪精度的良好途径.人体运动跟踪中最常采用的数据融合方法是互补滤波器和卡尔曼滤波器,随着微型芯片计算能力的提高,粒子滤波和基于优化的数据融合方法也逐渐被用于在线估计人体的姿态.
3.3.1 互补滤波
加速度计和磁力计容易受到高频噪声的干扰,陀螺仪容易受到随机漂移等低频噪声的干扰,互补滤波器就是将加速度计和磁力计测量的静态姿态通过低通滤波器去除高频分量,将陀螺仪测量的动态姿态通过高通滤波器去除低频分量,从而实现姿态信息的融合估计.Bachmann 等[2−3]提出了基于加速度计和磁力计的四元数互补滤波器补偿陀螺仪信号的漂移.文献[100−101]提出了一种滤波器框架,先将加速度计和磁力计的测量值通过Levenberg-Marquardt 算法进行姿态解算,将解算结果结合陀螺仪的测量值作为互补观测器的输入,进而得到姿态估计的结果.文献[111]结合TRIAD 姿态解算算法和互补滤波器重建人体关节在世界坐标系下的姿态.
上文提到的互补滤波器中,互补滤波器的参数保持不变,然而当人体处于不同的运动状态时,传感器的频率特性会发生变化,针对这一情况,一些学者提出了自适应互补滤波器[89,112−113]和时变互补滤波器[114].文献[89]提出了一种自适应互补滤波器,将陀螺仪和加速度计的测量值分别进行姿态解算得到的姿态角进行线性组合,线性组合的系数根据陀螺仪和加速度计数据自适应改变,原则是静态时加速度计的解算姿态系数占优,动态时陀螺仪的解算姿态系数占优.文献[112]将磁力计和加速度计的测量值通过高斯牛顿法解算四元数,接着与陀螺仪测量值解算得到的四元数进行线性组合,线性组合的系数根据高斯牛顿算法的收敛速度自适应调整.文献[114]基于模糊准则在线调整滤波器的截止频率,以适应加速度计和磁力计在运动过程中的时变物理特性.
3.3.2 卡尔曼滤波
1)线性卡尔曼滤波
Luinge 等在1999 年[1]提出了基于线性互补卡尔曼滤波器的人体姿态估计方法,首先直接通过角速度积分得到三个姿态角,将翻滚角和俯仰角定义为倾斜角,由加速度计测量值也可得到一组倾斜角,两者之差经基于误差模型的卡尔曼滤波器滤波后补偿由角速度积分得到的倾斜角.随后进一步考虑陀螺仪的偏差和线性加速度,分别将偏差和线性加速度建模成一阶马尔科夫过程和一阶低通白噪声过程,进而可在滤波过程中估计和补偿陀螺仪偏差和线性加速度,提高了姿态估计的精度[85].然而,Luinge等只采用了陀螺仪和加速度计,无法补偿航向角的误差,因此Roetenberg 等[90]在前文基础上加入了磁力计以校正航向角,该文提出的线性卡尔曼滤波器有两个输入,第一个输入为加速度计与陀螺仪之间的倾斜角差值,第二个输入为陀螺仪与磁力计之间的航向角差值.文献[50]提出了两层融合算法,在第二层融合引入下肢位置约束,通过线性卡尔曼滤波器得到约束融合后的人体位移.另外,文献[39,54,80,88,103,109,115]同样采用了线性卡尔曼滤波器.
2)扩展卡尔曼滤波
人体位姿估计系统往往建模为非线性系统,此时线性卡尔曼滤波器不再适用,EKF 和UKF 是两种最常见的非线性滤波器.不同于文献[90],Roetenberg 等在文献[91]中采用非线性模型描述姿态估计过程并用EKF 算法实现姿态估计.Yun 等[4]通过高斯–牛顿迭代法从加速度计和磁力计的测量值中解算出四元数,把该组四元数和角速度作为新的量测值,则输出方程转化为线性形式,此时仅状态方程为非线性,可简化EKF 的计算.该方法在上肢姿态估计中得到了应用[92−93].在下肢关节角度估计中,文献[51]提出了两种不同的下肢运动学模型,分别以骨盆和切换的站立脚为基坐标系原点,使用EKF 融合加速度计和陀螺仪的数据.为了增强位姿估计算法对运动过程中产生的未知的线性加速度和磁力计扰动的适应能力,文献[105,107]采用自适应EKF 算法,量测噪声的方差根据线性加速度干扰或磁力计扰动自适应调整,这些文献的自适应策略已在第3.2 节中提到.此外,Sabatini 等[97−99]同样采用了EKF 算法估计人体位姿.
3)无迹卡尔曼滤波
EI-Gohary 等[5]首次将上肢5 自由度运动学模型引入到上肢关节角度估计中,将关节角度作为状态变量,采用匀加速模型作为状态方程,量测方程中引入了上肢运动学模型来描述陀螺仪和加速度计测量值与状态变量之间的关系,采用UKF 算法估计上肢5 个自由度的旋转角度.为进一步提高各个关节角估计的精度,在前文基础上,文献[86]进行了以下几方面的改进:1)将陀螺仪和加速度计的偏差建模成高斯白噪声,并扩张为新的状态变量进行估计和补偿;2)根据上肢关节的运动角度范围对每个关节角引入状态约束,采用具有状态约束的UKF 算法;3)在航向角的估计中引入零速度更新算法以校正陀螺仪漂移对航向角的影响.此外,文献[6,71,96]采用了基于5 自由度上肢运动模型的UKF 算法.同样采用UKF 算法,文献[45]基于7 自由度的上肢模型,文献[116]将上肢模型简化为4 自由度.文献[63,68,104]采用了自适应UKF,同样地,这些文献的自适应策略也已在第3.2 节中提到.
3.3.3 粒子滤波
粒子滤波器无需像卡尔曼滤波器一样假设噪声为高斯分布,因此更具有一般性,随着微芯片计算能力的提高,使得应用粒子滤波器用于实时估计成为可能.文献[7,66]分别采用分层融合的思想估计上肢和下肢的运动姿态,第一层为数据融合层,第二层为几何约束融合层.文献[82]基于视觉和惯性传感器实现上肢运动跟踪,为避免粒子退化,对状态空间进行约简且引入了手臂的生物学约束.
3.3.4 基于优化的方法
随着微型芯片计算能力的提高,基于优化的方法逐渐被应用于人体位姿估计中.文献[47,94]提出了基于模拟退火算法的上肢关节位置估计方法,以计算得到的上臂长度与真实长度之间的偏差最小化作为优化目标,通过模拟退火算法求解该优化问题.文献[95]通过拉格朗日乘子法估计肩膀的位移.文献[32]以重力加速度分量与加速度计测量值之差的平方最小化为优化目标,通过牛顿迭代法求解最优四元数,由于只使用了加速度计,因此所得结果的应用范围只能限制在手臂静止或慢速运动时,一旦因手臂运动产生的线性加速度相对于重力的分量不可忽略时,优化结果会出现较大偏差.文献[17−18]在步态分析中采用梯度下降算法求解最优四元数.
4 应用场景
近年来,由于微惯性传感器的发展得到广泛关注及应用,越来越多的学者将基于惯性传感器的人体运动跟踪技术应用于康复治疗、步态分析、人体安全监测、人机交互、体育训练和虚拟现实等领域.
1)康复治疗
通过将包含惯性传感器的节点设备佩戴在康复阶段的病人身上,医生可以通过分析病人的日常生活状况及活动状况,对病人的行为能力和运动强度作出判断,从而了解病人的身体恢复情况,并随时针对病人的恢复情况作出诊断修改,以适应不同康复阶段的需要,给予康复期的病人最优的治疗方案.英国的Zhou 和Hu 等[47,94−95,103]以中风病人的上肢康复为背景,基于Xsens 公司生产的可穿戴式惯性传感器,设计了上肢关节位置估计系统,估计精度可完全满足中风病人上肢康复的需求.文献[117−119]基于惯性传感器设计了中风病人康复运动的评估系统,专业的理疗师可通过联网设备在线监测病人是否按照规定完成了指定的康复动作.文献[120]通过固定在康复患者鞋上的惯性传感器和足底压力传感器跟踪患者行走轨迹、步行距离和步幅,理疗师通过远程监控患者的步行数据可评估患者的康复情况.文献[121]列举了可穿戴式的传感器在上肢康复训练中的应用.
2)步态分析
步态分析是一项针对人体步行运动分析的技术,旨在研究步行的内在规律,步态分析的过程包含了测量,并对可测量的步态参数进行计算、分析与解释,进而得出结论,对被测者的步行能力得出综合评估.由于步行运动包含了大量的人体运动学信息,步态分析在疾病诊断[122−124]和身份识别[125−126]等领域都有重要意义.通过佩戴在下肢不同部位的惯性传感器,可采集各类患者和健康人群的运动数据.由于疾病的影响,患者在步行过程中表现出的步态参数异于常人,通过简单的分类可辨别是否罹患帕金森综合征[122]或中风[123]等疾病.文献[124]通过机器学习方法对肌萎缩侧索硬化(Amyotrophic lateral sclerosis,ALS)、帕金森综合征和亨廷顿舞蹈病(Huntington´s disease)三种疾病进行分类.在身份识别和安全领域,步态信息可以用来对人的身份进行鉴别.正如每个人都有独一无二的指纹和虹膜,每个人也都有独一无二的步行习惯.通过采集大量人群的步态参数,建立数据库,可寻找当前步态参数与数据库中最匹配的个体,从而识别人的身份[125−126].
3)安全监测
由于惯性传感器体积小、可穿戴,所以能轻松地佩戴在人身上,检测人日常运动时的运动学信息,对这些运动学信息的分析,可用于工人在工作过程中的损伤评估和老人异常行为的监控.
工人在完成搬运货物、操作大型机械设备等工作时,由于人体承受了较大的力,一旦动作不规范或长期处于这样的工作环境中,骨骼和肌肉很容易受到损伤.文献[127]借助IMU 和角度传感器对人体上肢的运动进行检测,实时评估工人在工作过程中发生肌肉骨骼损伤的风险,工人可接收该反馈信号,从而可在受到较大的损伤风险时及时停止危险动作.文献[44,128]介绍了人体位姿估计在职业工人健康监测中的应用,通过基于惯性传感器和磁力计监测工人的关节弯曲角度,可评估工人是否处于一个危险的动作,或工人受到损伤后,具体确定是由哪一部分工作造成的损伤.
在老年人跌倒检测的研究方面,文献[129]通过佩戴在左右膝盖和胸部的三个惯性传感器,对因打滑、绊倒、昏厥等7 种造成跌倒的动作进行识别,以便跌倒者可接受针对性的治疗.文献[130]提出了一个专为老年人跌倒保护设计的移动式人体安全气囊系统,利用支持向量机算法对跌倒和其他正常运动进行分类,当检测到跌倒动作时,佩戴在腰部的安全气囊会自动打开以降低老人在跌倒过程中发生损伤的危险.
4)人机交互
在工业4.0 背景下,人和机器人如何协作以更好地完成相关任务已成为一种重要的发展趋势.目前,机器人只是作为人的替代者完成一些高风险、高重复度的工作,例如汽车装配车间的装配机械手.例如何让人参与到完成一些任务的过程中是未来机器人技术发展的一个重要问题.目前,基于惯性传感器的人机协作只能实现一些低复杂度的运动,如让机器手模拟人手臂的动作[131−133].2004 年,加州州立大学的Miller 等[131]通过固定在人手臂上的两个惯性传感器捕捉上肢的运动姿态,从而遥控NASA 的上半身宇航机器人.文献[132]通过VR 眼镜实现远程操控Kuka Youbot 机械臂抓取物品.文献[133]通过惯性传感器得到人腕部的运动轨迹,通过一个3自由度的机器人复现腕关节的运动轨迹.为了提高机器人复现人动作的精度和复杂度,文献[80]结合Kinect 相机获得手部在全局坐标系下的位置,同时通过IMU 获得手部的角度信息,将手部的角度和位置信息发送给机械手,让机械手实现抓取和放置物品、钉钉子等复杂任务.文献[134]提出一种基于前臂表面肌电信号和惯性多源信息融合的隐式交互方法来实现协作机器人的演示编程.在2018 世界移动通信大会(WMC)上,来自日本的公司展示了基于5 G 通讯的人形助理机器人.将机器人与人类操作者通过5 G 网络连接,通过Xsens 公司的动作捕捉套装采集人体运动信息,人形助理机器人通过采集的人体运动信息模仿人类操作者的各种复杂动作.另外,在人机交互领域,识别骑行者在骑行过程中的姿态[135−136]也是一个典型的应用,其研究成果可应用于帕金森病人的康复训练和人体姿势矫正.
5)体育训练
通过捕捉运动员在训练过程中的运动数据,教练员可对运动员的训练过程进行评估,从而对之后的训练项目提出针对性的指导意见,例如飞镖投掷训练[137]、棒球手训练[138]、高尔夫训练[139]等.诺亦腾公司推出的mySwing Pro 系统是用于高尔夫球训练教学的全身动作捕捉分析系统,可在室外环境中精确捕捉球手全身动作以及球杆运动轨迹,并进行实时回放分析.通过3D 模型、分析图表等多种辅助参考工具,球手可以全面观察分析自身挥杆动作,并与技术更高的专业球手进行比对.另外,在体育竞技过程中,通过实时监测运动员的运动数据,可评估运动员的各项指标和比赛表现,进一步可对运动方案作出调整,避免运动员由于过度训练和不当动作造成不必要的损伤,进而影响比赛结果,例如在滑雪[140−141]、游泳[142−143]、跑步[144−145]等方面的应用.文献[24]列举了惯性传感器在体育竞技领域的应用.
6)虚拟现实与影视制作
通过惯性传感器设备捕捉人体的动作信息并进行重现,即人体捕捉技术的出现,给虚拟现实技术的发展带来了新的希望.通过固定在参与者身体特定部位的惯性传感器设备可采集到受环境干扰小的人体动作信息,经过相应数据处理后可加载到电脑动画中,从而实现基于虚拟现实技术的动画和游戏的开发制作.在影视制作中,通过固定在人体上的传感器节点,可以获取动作数据并进行重现,应用于影视制作中,能够实现电影中一些高难度动作.
5 总结与展望
基于可穿戴式惯性传感器的人体运动跟踪技术,借助佩戴在身体各部位的微惯性传感器和磁力计,通过姿态解算方法和数据融合方法可实时跟踪人体的运动姿态.由于具有佩戴方便、运动空间不受限、成本低等优点,已广泛应用于许多领域.本文对惯性式人体运动跟踪技术的产生发展以及当前的研究现状进行了比较详细的综述,由以上综述可见,惯性式人体运动跟踪方法已十分丰富,尤其在传感器误差处理和数据融合方法上,涌现了很多独具特色的研究,且目前市场也已出现成熟的惯性式人体运动捕捉的产品.但是由于人体运动的复杂性和惯性传感器本身的特点,使得研发高精度的惯性式人体运动检测系统依然存在较大难度.在未来开展基于可穿戴式惯性传感器的人体运动姿态检测时,可关注以下研究点:
1)模型不确定性问题
在基于惯性传感器对人体的位姿进行重建和跟踪时,模型的不确定来自两方面:一是人体关节不同于机械关节,有些关节并不是严格按照固定的旋转轴旋转,会存在一定的偏移[61,146],且有些关节的转动情况比较复杂[147];二是即使进行了传感器的初始校准,运动过程中由于皮肤和肌肉的形变会引起传感器的位移,则初始校准时得到的坐标变换矩阵已存在偏差.到目前为止,对于关节轴的误差并没有很好的解决方法,一方面因为关节轴的误差因人而异,另一方面引入更多的关节自由度势必会增加建模和实时应用的难度,且少有文献讨论皮肤或肌肉的形变对人体姿态估计的影响.因此,有必要针对不同体型的人群分析人体关节角度变化与皮肤或肌肉形变的定量关系,从而在人体运动过程中实时补偿由形变带来的偏差.
2)传感器初始对准误差
由第2 节的分析可,知初始对准方法的精度完全依赖于被测试者完成相应对准动作的精度,然而由于个体的差异,被测试者无法完全标准地完成设定的动作,例如N-pose 要求被测试者的手臂垂直向下,T-pose 要求被测试者的手臂保持水平.相比于静止校准方法,动态的校准方法虽然能够取得更为精确的校准结果,但是这个过程更为复杂且被测试者独立完成标准的校准动作难度较大.现有的一些自校准方法和无校准方法较少且实现起来较为复杂,研究便捷精准的传感器初始对准方法,甚至无需对准的人体运动姿态估计方法,将有助于降低人体运动跟踪系统的应用难度.
3)多传感器信息融合
传感器误差是导致基于惯性传感器的人体位姿估计精度难以提高的重要原因.在现有文献的基础上,可进一步研究结合其他不存在累积误差的传感器作为辅助传感器,例如视觉传感器、肌肉形变传感器、力传感器或肌电信号传感器等,相应获取的信号作为校正信息消除累积误差.例如肌肉电信号不易受到累积误差的干扰,通过肌肉电信号与关节动力学模型估计关节角度,此角度可对惯性传感单元进行校正.
4)复杂精确的人机协作场景
目前,基于惯性传感器的人机协作只能完成一些低复杂度的运动,对人体运动姿态估计精度要求不高.人机协作未来的研究方向必然是人与机器人更为紧密的协作,例如人和机器人共同完成一项任务,此时就要求基于惯性传感器的人体运动姿态估计技术具有较高的精度.因此,有必要研究高精度的惯性式人体运动姿态估计方法,从而实现复杂的人机协作.

