大规模动态网络的相似性度量方法研究*

王 佳，武志昊，赵苡积，林友芳

北京交通大学 计算机与信息技术学院，北京 100044

1 引言

近年来，复杂网络已成为多学科交叉的热点研究领域之一，有很多学者进行了大量深入的研究。复杂网络（以下简称为网络）通常由节点和节点之间的连边组成，其中节点表示真实网络中的个体，节点之间的连边表示个体之间存在的联系。网络结构相似性计算作为复杂网络中的一个研究方向，在许多网络分析应用如异常检测、状态划分中起着重要的作用。目前大多数研究仅针对静态网络，但在实际场景下，网络的结构往往会随着时间的推移而发生改变，如何衡量动态网络的结构相似性是计算机科学领域的一个急需解决的问题。

目前，已经有多种静态网络相似性度量方法被提出，这些方法通常从宏观和微观两个角度衡量网络的差异。微观方法[1-2]通常根据网络的细节信息（如重叠的节点或边的数量）差异来衡量网络之间的相似程度，这类方法仅关注网络结构的细节信息，而忽略了网络中丰富的宏观信息，如社团结构。宏观方法[3-4]则关注整体网络结构的变化，细微的网络变化不会对整体相似性产生较大影响。受到广泛关注的谱距离[3]就是一种典型的宏观方法，该方法虽然有不错的效果，但是它的计算复杂度为Ο(n3)，很难应用在快速变化的大型动态网络中。为了解决在大型动态网络中计算成本高的问题，本文引入矩阵扰动理论[5]，结合网络扰动提出了一种快速衡量网络相似性的方法。具体来说，本文方法根据初始网络快照的特征值和特征值对应的特征向量估算后续网络快照的特征值，不需要在每个网络快照上重新计算特征值，将计算复杂度降低至线性复杂度。

本文其余部分的结构安排如下：第2章介绍网络相似性研究领域的相关工作；第3章介绍基本概念的定义和方法描述；第4 章进行实验介绍及结果分析；第5章给出全文的总结及展望。

2 相关工作

目前已经被提出的网络相似性度量方法大致可以按微观和宏观角度分为两类。微观方法，如图编辑距离[1]和DELTACON[2]主要关注的是网络的细节差异。网络编辑距离定义为将一个网络转变为另一个网络所需的编辑次数，在动态网络中可以理解为边的变化数量。DELTACON使用置信度传播算法将网络表示为节点间的亲密度矩阵，然后计算矩阵间的距离进而得到网络的相似性。

以上方法仅关注网络的细节差异而忽视了网络中丰富的宏观信息，而宏观信息往往能更完整地反映网络整体的结构差异，因此本文更关注的是宏观方法。例如，Rossi等人[4]提出了一种通过连续时间的量子游走演化来度量相似性的方法，该方法将两个网络之间的相似性定义为网络所对应的密度矩阵之间的Jensen-Shannon 距离。Domenico 等人[6]将该Jensen-Shannon距离应用于层次约减任务中，通过计算动态网络快照之间的相似性将网络层数约减到最小。实验结果表明该方法可以将网络层数约减至原来的75%，但该方法也需要计算网络的特征值，导致计算复杂度高。Wilson 等人[7]依据谱特征可以用于表征网络的属性和提取网络的结构信息的特点，提出谱特征可用于解决网络的相似性问题。Masuda等人[8]将该方法应用于状态检测任务中，实验结果表明该方法可以有效区分网络中的不同状态，但该方法仅适用于小型网络。Chen等人[9]引入矩阵扰动理论，通过跟踪特征值的变化来快速计算网络中的某些属性，如网络中的三角形数量。与该方法不同的是，本文侧重于估算网络快照间的特征值差量。

通过谱距离衡量网络相似性虽然有效，但是存在计算复杂度高的缺点。一方面，目前通过迭代算法进行优化最好情况下可以将复杂度降为Ο(n2)[10]，但对于计算大型动态网络的相似性而言复杂度仍然很高。另一方面，计算网络的全部特征值是不必要的，在大多数应用中仅需前k个特征值即可[9]。为了解决计算问题，本文引入矩阵扰动理论，将其与网络扰动理论相结合提出了一种快速衡量大型动态网络相似性的方法。

3 问题定义及方法描述

3.1 问题定义

定义1（动态网络）单个网络快照定义为一个二元组G=(V,E)，其中集合V={v1,v2,…,vN}称为节点集，集合E={e1,e2,…,eH}称为边集。网络可以用邻接矩阵A来表示，矩阵中的元素值为1表示节点之间有连边，值为0 表示节点之间无连边。如图1 所示，动态网络是随着时间变化的网络集合。假设动态网络的时间跨度为[0,m]，按照一定的时间间隔将整个时序网络划分为T个时间窗口，那么动态网络就是T个网络的序列，即ζ={G1,G2,…,GT}。假设ζ中的每个网络Gi都有相同的节点集合V，即另外，本文中只讨论无向网络，但本文提出的方法可以推广到其他类型的网络中。

Fig.1 Dynamic network diagram图1 动态网络示意图

定义2（矩阵特征值）设A∈Cn×n，如果存在λ∈C和非零向量x∈Cn，使得Ax=λx成立，则称λ是A的一个特征值，x为A的属于特征值λ的特征向量。其中A的所有特征值的集合称为A的谱，记作λ(A)。

定义3（网络谱距离）由定义2可知，将任意网络表示为矩阵形式后可计算其矩阵的特征值。谱距离（spectral distance，SD）就是计算两个不同网络矩阵表示的特征值之间的距离。对于任意的矩阵表示，有以下两种类型的谱距离，分别为谱距离和标准化谱距离。假设有两个网络Gm=(V,E)和Gn=(V,E′)，Gm与Gn之间的谱距离定义如下[11]：

其中，分母为标准化项，表示在两个网络中取较小的特征值平方和。

定义4（矩阵扰动）假设有两个矩阵Xm和Xn，Xn可以看作是Xm经过扰动得到的，扰动可以表示为ΔX=Xn-Xm。通过一阶矩阵扰动理论[5]，利用Xm的特征值可近似得到Xn特征值，定义如下：

定义5（网络扰动）假设有两个网络Gm=(V,E)和Gn=(V,E′)，那么Gn可以看作是Gm经过一系列边的扰动得到的。如果将网络表示为邻接矩阵Am和An，由定义4可知An可以看作是Am经过扰动ΔA=An-Am得到的。

定义6（问题定义）针对动态网络ζ={G1,G2,…,GT}中任意的两个网络快照Gm=(V,E)和Gn=(V,E′)，设计一种网络相似性度量方法SpeedSim(Gm,Gn)∈[0,1]衡量两个网络快照的相似性。该方法应满足当且仅当Gm与Gn完全相同时值为1。

3.2 方法描述

将动态网络ζ={G1,G2,…,GT}的各网络快照表示为矩阵集合X={X1,X2,…,XT}，其中初始网络快照也可表示为Xinit。将网络扰动和矩阵扰动理论相结合，根据Xinit的特征值λinit和特征向量μinit快速更新得到后续网络快照的特征值，通过计算谱距离得到动态网络各网络快照间的相似性。

一般而言，谱距离是基于两个网络矩阵表示的特征值之间的比较，例如邻接矩阵或拉普拉斯矩阵[3]。由于在计算谱距离时拉普拉斯矩阵已被证明优于邻接矩阵，因此只考虑拉普拉斯矩阵的谱距离。首先，区分拉普拉斯矩阵和归一化拉普拉斯矩阵[12]。拉普拉斯矩阵L=D-A，其中A是邻接矩阵，D是对角矩阵，其对角线元素等于各节点的度。归一化的拉普拉斯矩阵，其中I是单位矩阵。由于归一化拉普拉斯矩阵的数值范围为0～2，在数值计算方面更为稳定，因此本文选用标准化的拉普拉斯矩阵表示。

3.2.1 动态网络的特征值扰动

给定动态网络ζ中初始网络快照的矩阵表示Xinit和除初始网络快照外t时刻网络的矩阵表示Xt，那么t时刻的矩阵可以看作是初始时刻矩阵经过扰动得到的，扰动可以表示为ΔXt=Xt-Xinit。通过一阶矩阵扰动理论可得，使用Xinit的特征值λinit可近似得到Xt的特征值λinit，定义如下：

假设Xt被一组边扰动，其中s是扰动矩阵ΔXt中的非零元素的数量。那么可被扩展为：

3.2.2 SpeedSim：动态网络相似性度量方法

动态网络ζ={G1,G2,…,GT}，其中G1为初始网络快照，其矩阵表示为Xinit。给定动态网络ζ中任意两个网络快照Gm和Gn(1≤m,n≤T），网络的矩阵表示Xm和Xn，由式（4）可得：

其中，当m=1时，

结合式（2），此时的标准化谱距离定义如下：

此时的相似性定义如下：

3.2.3 算法描述

将动态网络ζ中的各网络快照表示为归一化拉普拉斯矩阵后得到集合X，使用谱分解方法计算初始网络快照Xinit的特征值λinit和对应的特征向量μinit，然后使用λinit快速更新得到后续网络快照的特征值。最后通过计算各网络快照间的谱距离dis得到动态网络的相似度矩阵sim。算法1为基于矩阵扰动计算特征值的一般步骤。算法2 为基于特征值计算动态网络相似性的一般步骤。

算法1基于矩阵扰动计算特征值

输入：动态网络的矩阵表示X1,X2,…,Xtmax，初始网络快照的前k个特征值及其对应的特征向量，其他网络快照相对于初始网络快照的一系列扰动矩阵

算法2基于特征值计算动态网络相似性

输出：相似度矩阵sim。

由于计算特征值是主要的时间消耗，并且算法2中基于算法1 得到的特征值计算相似性与一般的相似性度量算法步骤相同，因此重点分析算法1 的时间复杂度。假设T为动态网络的时间跨度，s为中的平均扰动边数，由步骤1到步骤6计算的时间复杂度为Ο(Tks)，更新的时间复杂度为Ο(T)，那么算法1的时间复杂度为Ο(Tks)。对于空间复杂度，需要花费Ο(Tk)存储，Ο(s)存储ΔXt，因此空间复杂度为Ο(Tk+s)。

4 实验设计与结果分析

4.1 数据集

4.1.1 人工数据集

LFR benchmark[13]是目前最常用的一种能够生成具有社区结构的人工网络生成模型。该生成模型的特点在于考虑了真实网络的不均匀性。在生成网络时假设节点度数分布与社区大小分布分别服从指数γ和α，节点的个数为N，节点的平均度为，节点的最大度为kmax。网络中的边使用混杂系数0≤μ≤1生成，即任意节点以(1-μ)的概率连接社区内的节点，以μ的概率连接社区外部的节点，因此μ值越大社区结构越难发现。

本文基于LFR benchmark 模型构造人工数据集LFR-SPEED-Diff 和LFR-SPEED-Node，用于测试相似性方法的计算效率。LFR-SPEED-Diff参数设置如表1所示，以相同的LFR参数生成初始网络快照。在每个初始网络快照的基础上分别以不同的随机重连比率0.1、0.3、0.5、0.7 和0.9 改变网络中的连边得到新的网络快照，最终得到5个变化的边数量不同的动态网络，每个动态网络均包含10 个网络快照。LFRSPEED-Node 参数设置如表2 所示，以不同的LFR 参数分别生成6 种不同参数下的初始网络快照。在每个初始网络快照的基础上以随机重连比率β=0.2 改变网络中的连边得到新的网络快照，最终得到6个节点数量不同的动态网络，每个动态网络包含10 个网络快照。

Table 1 Parameters table of LFR-SPEED-Diff表1 LFR-SPEED-Diff参数表

Table 2 Parameters table of LFR-SPEED-Node表2 LFR-SPEED-Node参数表

4.1.2 真实数据集

小学动态接触网络数据集（PRIMARY）[14]由SocioPatterns 协会收集。通过给小学中的学生和老师穿戴射频识别装置（radio frequency identification，RFID），每隔一段时间探测一次，如果他们之间的距离在1～1.5 m 内会记录下这条连边。该动态网络数据集中共有242 个节点，分别为法国某小学来自10个不同班级的232名学生和10名老师。该数据集采集于2009年10月的连续两天，第一天的时间跨度为8:45—17:20，第二天的时间跨度为8:30—17:05，每20 s 采集一次，共采集了3 100 片网络。在实验中为了保持两天的时间跨度相同，将时间跨度统一设置为9:00—17:00。在该网络中，学生有两种不同的活动状态，分别为上课状态和午餐活动状态，不同活动状态所对应的具体时间如表3所示，以此来验证状态划分结果的准确率。

Table 3 Status verification information表3 状态验证信息

4.2 对比方法

4.2.1 标准化谱距离

标准化谱距离的定义如第3章中式（2）所示。

4.2.2 JS散度

JS 散度（Jensen-Shannon divergence）是一种基于熵的网络相似性度量方法[4]。为了定义熵，首先通过来定义密度矩阵，其中β为在网络上运行扩散过程的时间量的参数，ρ的特征值总和为1。冯诺依曼熵由定义，其中λi是ρ的第i个特征值。JS散度的定义如下：

4.2.3 Deltacon

Deltacon[2]是一种可扩展的网络距离度量方法。假设有两个网络G=(V,E)和G′=(V,E′)，使用置信度传播算法分别计算G和G′中任意节点之间的亲和度，得到亲和度矩阵W和W′。然后计算亲和度矩阵W和W′之间的距离。Deltacon的定义如下：

4.3 实验设置

4.3.1 状态划分实验

自然界、社会和技术网络中的许多时间演化系统都留下了它们之间相互作用的痕迹，这些相互作用形成了反映系统状态的动态网络[8]。本实验通过将本文提出的SpeedSim 方法与层次聚类相结合，在真实数据集上检测系统状态来对这些系统进行粗略的描述。实验流程如图2所示。

（1）将动态网络ζ按照时间粒度τ划分为T个网络快照，即ζ=(G1,G2,…,GT)，其中τ的选择是任意的，并将动态网络ζ表示为矩阵集合X=(X1,X2,…,XT)。本文中真实网络的基本属性如表4所示。

Table 4 Real network basic properties表4 真实网络基本属性

（2）计算动态网络ζ中各网络快照的特征值λ1,λ2,…,λk，其中k=50。根据特征值计算任意两个网络快照之间的距离构成距离矩阵dis(Gm,Gn)，由距离矩阵可得到相似性矩阵sim(Gm,Gn)，其中1≤i,j≤T。

（3）应用标准的层次聚类算法对网络快照进行聚类，聚类结果即对应于不同的状态。在层次聚类算法中，选用Average-linkage 参数，即用平均距离定义两个集合之间的距离。层次聚类的聚类个数由邓恩指标（Dunn validity index）[15]确定，该指标用于确定最优的聚类个数。定义如下：

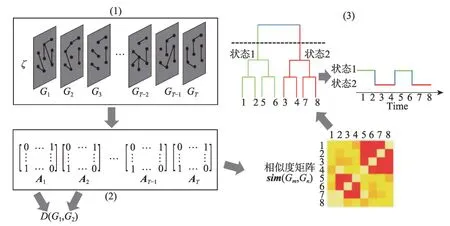
Fig.2 Experimental flow chart图2 实验流程图

（4）层次聚类的准确率用标准化互信息进行评价。标准化互信息[16]（normalized mutual information，NMI）是一种基于信息论的网络划分算法检验指标，可用于衡量两种划分之间的相似性，是社区发现的重要衡量指标。该指标也常用于评价一个聚类结果与标准聚类结果之间的相似性。NMI指标的值域是[0,1]，取值越高代表聚类结果越准确。互信息（mutual information，MI）用来衡量两种划分的相关性大小。定义如下：

划分X和划分Y的信息熵定义如下：

对互信息标准化得到NMI的定义如下：

4.3.2 性能验证实验

为了验证SpeedSim 方法的时间效率，本文使用人工数据集LFR-SPEED-Diff和LFR-SPEED-Node模拟大规模动态网络，使用运算时间（单位：s）评价相似性方法的时间效率。

4.4 实验结果

4.4.1 状态划分实验

4 种相似性度量方法在小学动态接触网络上的状态划分结果如图3～图6 所示，从左至右分别为20 min、10 min 和5 min 时间粒度下的状态划分结果图，每个结果图均由相似性热度图和状态转换序列组成；相似性热度图中横坐标和纵坐标均表示网络快照编号，状态转换序列中横坐标表示网络快照编号，纵坐标表示不同状态。状态划分的准确率如表5所示。本文提出的SpeedSim方法与标准化谱距离在三种时间粒度网络下，均能自动发现网络中的两种不同状态。由相似性热度图可以看出，本文方法及标准化谱距离计算得到的相似度大小在不同状态下区分明显。结合图7 也可以看出本文方法可以清晰地将网络快照划分为两类，即对应于该网络中的两种状态。观察发现这两种状态与真实网络中学生的上课与午餐活动状态相匹配，这与使用图形信号对同一真实数据集进行处理得出的分析结果是一致的[17]，表明SpeedSim 与标准化谱距离在状态划分任务中是有效的。

Fig.3 State division result graph of SpeedSim图3 SpeedSim方法的状态划分结果图

Fig.4 State division result graph of standard SD图4 标准化谱距离方法的状态划分结果图

Fig.5 State division result graph of JS图5 JS散度方法的状态划分结果图

Fig.6 State division result graph of Deltacon图6 Deltacon方法的状态划分结果图

Fig.7 State hierarchy clustering diagram of SpeedSim method图7 SpeedSim方法的状态层次聚类图

如图5 和图6 所示，JS 散度和Deltacon 在三种时间粒度网络下的相似性热度图没有明显的区分度，由状态转移序列也可看出这两种方法无法区分真实数据集中的不同状态。其中Deltacon 无法将状态自动聚类成两类，这可能是由于该方法逐对地比较两个网络中的节点亲密度，这种比较过于细化。此外，由表5可以看到SpeedSim与标准化谱距离的划分准确率均为1.00，而JS 散度和Deltacon 的准确率很低。该准确率结果与针对状态划分结果图的分析结果是一致的。综上所述，可以发现本文提出的SpeedSim方法虽然使用矩阵扰动理论更新得到前50个特征值来计算网络的相似性，但并没有因为提升了计算速度而降低状态划分的准确率。因此本文方法与谱距离相比具有明显优势。

4.4.2 性能验证实验

在状态划分任务中，SpeedSim 和标准化谱距离的划分准确率较高，在此进一步比较两种方法的计算性能。本文提出的SpeedSim方法具有与变化的边数量相关的线性复杂度，相较于谱距离与节点数量呈正比的平方阶复杂度，计算效率大大提升。为了验证该方法的计算效率，本文设计人工数据集LFRSPEED-Diff和LFR-SPEED-Node。由图8可以看出，在节点数和边数相同的情况下，随着随机重连比率β增大，即网络中变化的边数量增多，SpeedSim的计算时间也逐渐升高，并与网络中变化的边数量呈线性相关。如图9 所示，随着节点规模的增加，网络中边的数量成倍增长，网络规模逐渐增大，计算时间也随之升高。当N=100 000时，谱距离的计算效率明显低于SpeedSim，不仅计算耗时而且内存消耗也非常大；在节点数量达到150 000 时基本已经达到了可计算网络规模的临界值。而本文提出的方法随着网络规模的逐渐增加，计算效率缓慢下降，且内存开销小，因此SpeedSim 方法的计算复杂度明显低于标准化谱距离。

Fig.8 LFR-SPEED-Diff performance result graph图8 LFR-SPEED-Diff性能结果图

Fig.9 LFR-SPEED-Node performance result graph图9 LFR-SPEED-Node性能结果图

5 结束语

本文基于矩阵扰动理论提出了一种快速的动态网络相似性度量算法，该方法通过跟踪动态网络的特征值变化计算动态网络中各时间片网络结构的相似度。为了验证本文方法的有效性，本文通过LFR基准模型生成了两种人工数据集LFR-SPEED-Diff和LFR-SPEED-Node验证该方法的性能，并将其应用于状态划分任务中。在人工数据集和真实数据集上的实验结果表明，本文提出的方法具有与变化的边数量相关的线性复杂度，大大加快了计算速度，并且在状态划分任务中达到了和谱方法可比的准确率。

未来的研究需要在以下两方面开展：（1）深入研究本文方法能够揭示的网络结构特性。（2）将本文方法应用于其他动态网络任务中验证其有效性。