双臂式双旋转头贴片机贴装效率优化研究

余松乐 肖曙红 林德育

(广东工业大学机电工程学院 广东 广州 510006)

0 引 言

随着对贴装效率的要求越来越高，单臂型贴片机已经不能满足要求，多臂式多头拱架型贴片机成为当前主流的贴片机。该类贴片机在针对一块PCB板贴装时只是两个贴装头交替贴装，实质上是一台双臂式或者多台双臂式串联而成，所以本文主要针对双臂式双旋转头拱架型贴片机的贴装质量进行优化。贴片机的路径优化问题类似于TSP旅行商问题，即假设有一个旅行商人要拜访n个城市，每个城市只能拜访一次，最后要回到原来出发的城市，路径的选择目标是要求得的路径路程为所有路径之中的最小值。相对于模拟退火算法、遗传算法、蚁群算法解决此类问题效果更好[1]。单臂式拱架型贴片机在贴装过程中要考虑到贴片头的整体运动和自身的旋转运动、供料器的摆放位置、元件的贴装顺序等问题，建立的数学模型具有高维数、离散性、非线性的特点[2]。

目前对贴片机的路径优化问题，很多学者都进行了研究。文献[3]提出了一种整体模型使用启发式优化算法对多臂式拱架型贴片机进行优化研究；文献[4]提出了一种分层规划方法去提高多头贴片机的贴装效率；Liu等[5]同样提出一种启发式优化算法；董娟娟等[6]则提出一种改进的遗传算法对多臂式多头拱架式贴片机进行优化研究；张坤等[7]采用蚁群算法对多头垂直贴片机进行贴装优化；臧明相等[8]提出一种基于分层混合蛙跳的多头贴片机贴装调度算法。以上算法对多臂式多头贴片机的数学模型描述过于简单，数学模型只考虑贴片头的串行关系，即简单地将每个贴片头的贴装时间叠加起来为贴片机的整体贴装时间，没有反映出贴片头之间的并行关系，无法反映出真实的贴装情况。双臂式双旋转头拱架型贴片机不仅需要考虑一个贴片头内部取贴循环的优化，还需考虑两个贴片头之间的顺序优化。

本文在结合双臂式双旋转头拱架型贴片机的实际贴装情况下建立了合适的数学模型，然后结合实际的贴装过程，提出了基于取贴循环优化的改进蚁群算法对贴装顺序进行优化求解，不仅提高了贴片机的贴装效率，而且还有效地克服了传统算法中约束条件较多的缺点。

1 双臂式双旋转头拱架型贴片机贴装过程

双臂式双旋转头拱架型贴片机的贴装过程为：给定一组贴片元件的顺序，旋转的贴片头移动到供料器上方，贴片头上的第1个吸嘴吸取一个元件，然后旋转一定角度到第2个吸嘴吸取元件。重复上述操作，直到第12个吸嘴吸取元件，然后贴片头运动到上视相机上方对元件进行角度和位置的识别矫正，最后移动到PCB板上进行贴装。此过程称为单贴片头的内部取贴循环，如图1所示。此类贴片机主要由供料器、带吸嘴的贴片头转盘(每个贴装头安装12个吸嘴)、PCB板组成。在工作过程中，当贴片头1处于吸取元器件状态时贴片头2处于贴装元器件状态，贴片头2处于吸取元器件状态时贴片头1处于贴装元器件状态，这样两个贴片头之间形成一个取贴循环的过程，如图2所示。

图2 取贴循环示意图

2 基于取贴循环的蚁群算法优化

文献[1]已表明蚁群算法解决TSP问题的效果较其他算法好，故本文在蚁群算法的基础上进行改进。双臂式双旋转头拱架型贴片机整体的路径优化较为复杂，因此可以将其简单化。根据实际的贴装循环过程将其分为两个部分进行路径优化。第一部分是单个贴片头内部的吸取和贴装元器件的循环路径优化，第二部分是两个贴片头之间的吸取和贴装元器件的循环路径优化。这两个过程相互之间有联系又有区别，且都影响着贴片机的贴装效率，因此应使这两个贴装循环的路径最优化。本文针对这两个过程建立了相对应的目标函数，并利用改进的蚁群算法对目标函数进行了求解。

2.1 取贴循环内部的路径优化

由于两个贴片头的贴装过程是相同的，所以这里只对一个贴片头进行研究。

(1)

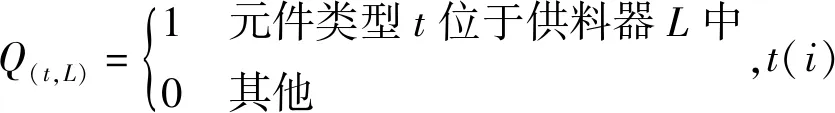
(2)

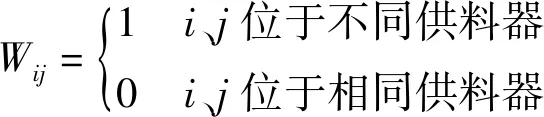
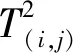
(3)

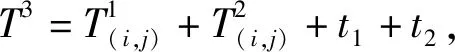
(4)

所以单贴片头内部取贴循环的目标函数为：

(5)

2) 种群规模的确定。贴装元件的数量n确定了蚁群算法的种群规模m，在保证最低性能的情况下应当适量减少蚁群的数量，本文选择的种群规模为m=0.6n。

3) 蚂蚁的选择转移策略。在解决TSP问题时，蚁群算法中的每只蚂蚁选择下一个城市是根据状态转移概率选择的，如下式所示：

(6)

式中：allowedk表示蚂蚁k下一步允许移动的城市；η为启发性信息；τ为由第i个城市到第j个城市的路径的信息素强度；α为信息启发式因子，β为期望启发因子。但贴片机在贴装时选择下一个元件时要考虑吸取元件和贴装元件的时间，两者的侧重比例不同，因此引入一个参数δ表示两者之间受重视的程度，所以状态转移概率为：

(7)

4) 新的信息素更新策略。局部更新策略：每个贴片头有12个吸嘴，一个循环内可实现12个元件的取贴，根据这个特点，可得蚁周系统的模型和t时刻在路径(i，j)路径上的更新策略分别为：

(8)

(9)

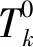
全局更新策略：为了使算法在尽可能大的范围内尽可能快地收敛到全局最优解，引入一个惩罚因子ω1，对全部解区间的信息素进行自适应的更新调整。t时刻在路径(i,j)上的更新规则为：

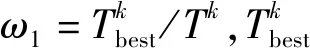
2.2 取贴循环间的路径优化

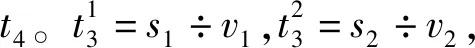
(t1+t2)×k2)+t4

(10)

式中：k1、k2分别表示贴片头1、贴片头2的循环次数，k为交叉循环的次数。

所以贴片机的整个贴装的目标函数可以写成:

(11)

种群规模的选择和前面相同，蚂蚁的选择转移策略选择一般的状态转移概率选择，如式(6)所示。全局信息素的更新采用基于蚁周系统模型进行信息素的更新，更新公式为式(8)，所以信息素的增量为：

(12)

2.3 改进后的算法特点

改进后的算法的特点主要有：(1) 在进行取贴循环内部元器件顺序优化时，依据元器件的分组，蚂蚁在选择下一个元器件时会先选择同组元器件，减少了蚂蚁搜索元器件的数量，缩短了算法的搜索时间，提高了算法的效率。(2) 采用基于取贴循环的蚁群算法将贴片机的整体优化复杂问题分解为多个简单的子优化问题，缩小了求解优化问题的规模，提高了最优路径的搜索效率。(3) 局部和全局相结合的信息素更新方式，避免了只有最优蚂蚁在每次循环后更新信息素致使陷入局部最优解。

3 实验结果分析

本文实验将对表1中5块PCB板的元器件进行路径优化。实验过程中，设基本蚁群算法的参数Q、α、β、迭代次数与改进算法相同，蚂蚁种群规模相同为m=0.6×n，其中n为元器件个数，基本蚁群算法状态转移概率公式则采用式(6)，信息素更新采用全局更新规则，贴片机的基本性能参数与改进算法相同。

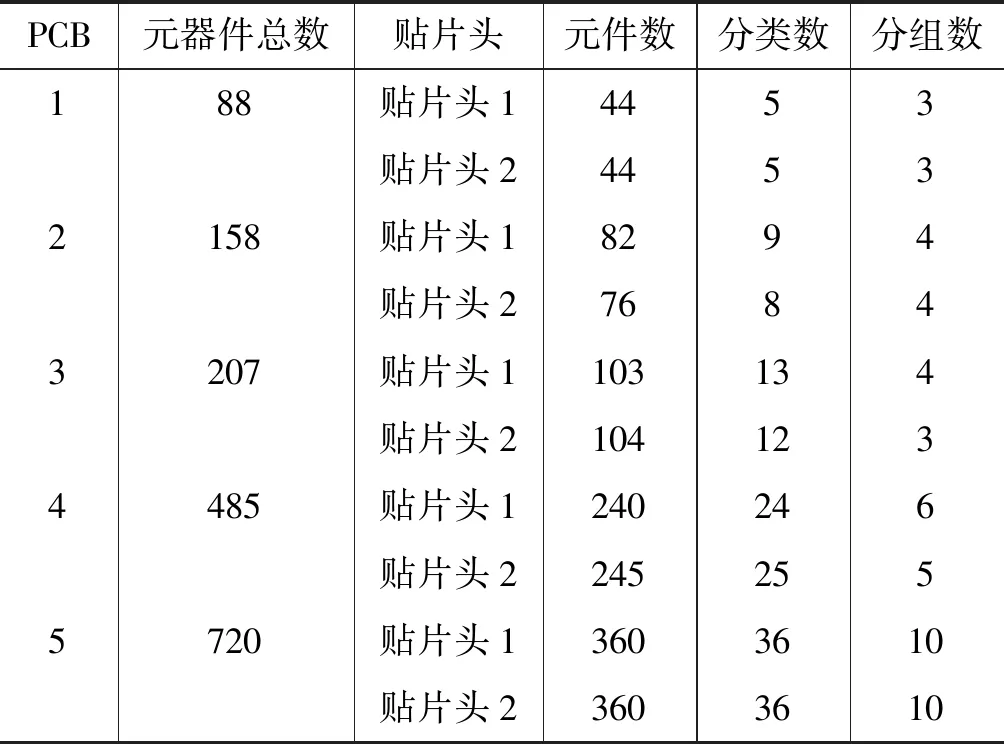
表1 PCB板元件特性

双臂式双旋转头贴片机的一些参数t1=t2=10 ms,v1=v2=1 000 mm/s，为了体现元器件尺寸对贴装性能的影响，t1、t2以20%的比例增加，v1、v2以20%的比例减小。实验中采用局部和全局信息素相结合的更新方式。程序的开发环境为Visual Studio2010/MFC，程序的测试环境为：双核2.8 GHz CPU，3 GB内存，Windows 7的操作系统。

以表1中2号和5号PCB板为例，使用改进的蚁群算法路径优化效果如图3所示，图中上下两排点表示供料器的位置，灰色的点表示贴片头1贴装的元件，黑色的点表示贴片头2贴装的元件，不同大小的点表示不同尺寸的元件。(a)和(b)表示2个贴片头单独贴装的路径图，(c)和(d)为2个贴片头一起贴装的路径图。

(a) 88-10 (b) 207-25

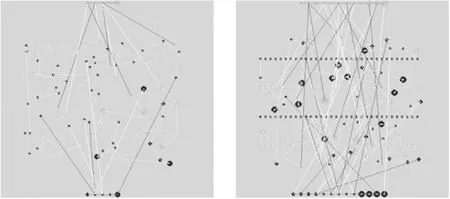
(c) 88-10 (d) 207-25图3 路径优化效果图

为了验证本文算法的优越性，将本文改进的蚁群算法与基本的蚁群算法、遗传算法分别对表1中5块PCB板进行20次计算，计算的最优、最差、平均解如表2所示。

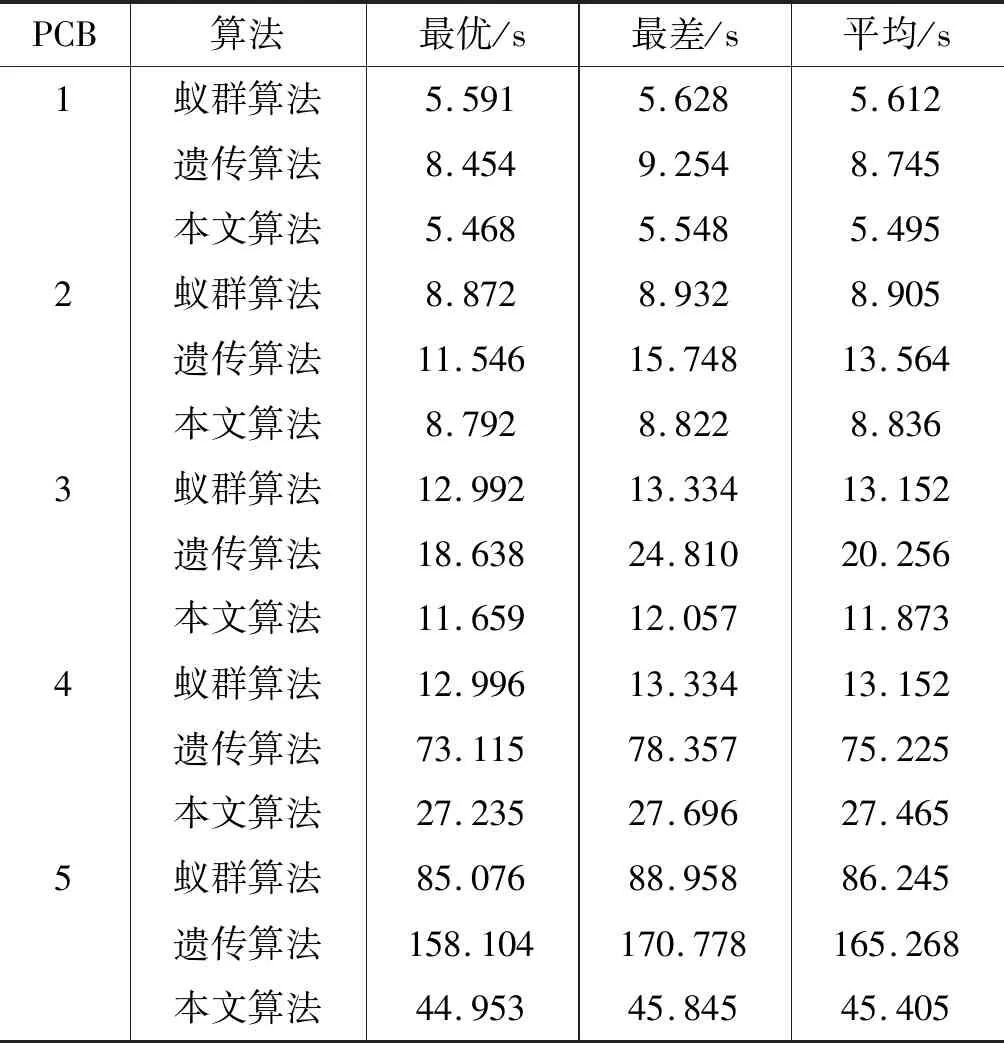
表2 算法结果比较表

4 结 语

本文分析了双臂式双旋转头拱架型贴片机的实际贴装过程，将其复杂的路径优化分为简单的单贴片头内的取贴循环的路径优化和双头之间的取贴交叉循环的路径的优化，建立了对应的模型。利用基于取贴循环的蚁群算法对模型分别进行求解。实验结果表明,本文提出的基于取贴循环的蚁群算法符合双臂式双旋转头贴片机的实际贴装过程，求得的最优解明显优于其他算法的最优解，缩短了PCB板的贴装时间，大幅提高了贴装效率。