云计算基于随机进化博弈动态的资源优化配置
尹 成 国
(海南热带海洋学院计算机科学与技术学院 海南 三亚 572022)
0 引 言
云计算通过其数据中心可以按需提供计算、存储、通信等资源服务于大规模分布环境[1]。云环境中的资源分配机制要求向云用户提供资源用于处理作业和存储数据,常用的资源提供手段包括按需提供和预留式提供[2]。按需提供时的定价是以即付即用为基础的,按需资源提供可以适应于具有波动和不可预测的资源需求状况。而预留式提供则可能有效利用空闲资源,且其价格低于按需提供。
由于云环境中参与实体的异构性和动态特性,资源的分配与管理是异常复杂的。很多研究利用经济学的思想完成资源分配优化问题,即博弈论的思想,这源于云环境中的资源管理与社会经济学活动拥有极大的相似性[3]。博弈理论可以通过搜索均衡解,利用迭代的方法将云资源分配形式化为效用优化问题。当前的相关研究主要包括三种类型的经济学博弈模型:(1) 基于合作式博弈的资源分配方法,通过将多个云用户组成为联盟的形式进行资源分配,以增加实体效用[4-5]。(2) 基于非合作式博弈的资源分配方法,利用云实体间的相互影响,采用对实体的基础的理性假设,让博弈者得到最大化的收益,并对行为策略拥有很好的判断和预测[6-7]。(3) 基于进化式博弈的资源分配方法,拥有有限理性的云实体间的博弈求解问题[8-9]。然而,通常情况下,现实环境中的云用户对于资源使用的行为难免会发生错误,这表明用户的策略均衡不是仅能通过一次性的动态调整得到的[10]。同时,以上研究均是在无限制的云种群环境中进行的,这也与实际情况不符。本文将利用随机动态机制研究有限云种群中的资源分配进化博弈问题,并通过用户策略的固定指数与入侵指数,求解不同种群大小中策略的进化方向。
1 资源分配模型
假设云计算系统拥有N个用户竞争资源,资源通过市场机制分配和提供,即通过资源价格的波动反映资源供求关系的变化。换言之,此时的资源分配取决于所有云用户对资源的出价策略。
定义1假设每个用户向资源方提交的一个竞价si,那么,s={s1,s2,…,sN}表示所有竞争用户的竞价集。如果si∈R,s为N个元素的向量。如果si为多维数值,则s为M×N矩阵,M为向量si的维度。
本文将维度限定为一维空间,那么,资源分享σi∈[0,1]即代表第i个竞价用户所分配的资源份额,且定义为:
(1)
假设每个用户对于获得的资源份额σi拥有一个评估函数vi(σi),该评估可视为给定资源份额下对于性能的价值评估,如在计算市场中处理作业的完成时间或给定带宽份额下数据的传输时间。每个性能度量可转换成一个可与竞价相比较的等价值。如果用户的评估是连续可微分的,则本文的博弈算法中用户的效用函数可定义为评估与其竞价的差值,即:
Ui=vi(σi)-si
(2)
2 进化博弈的效用矩阵
为了简化分析,本文的博弈模型中云用户被抽象为两种具有有限理性的用户种群。换言之,博弈即是研究具有两种策略x和y的进化动态过程,这表明每个用户在竞价博弈过程中将面临两种竞价策略博弈的进化动态过程。博弈框架的效用矩阵可表达为对称2×2矩阵,如表1所示。

表1 两种策略下的博弈效用矩阵
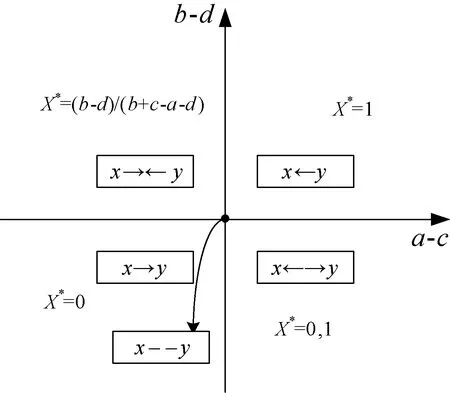
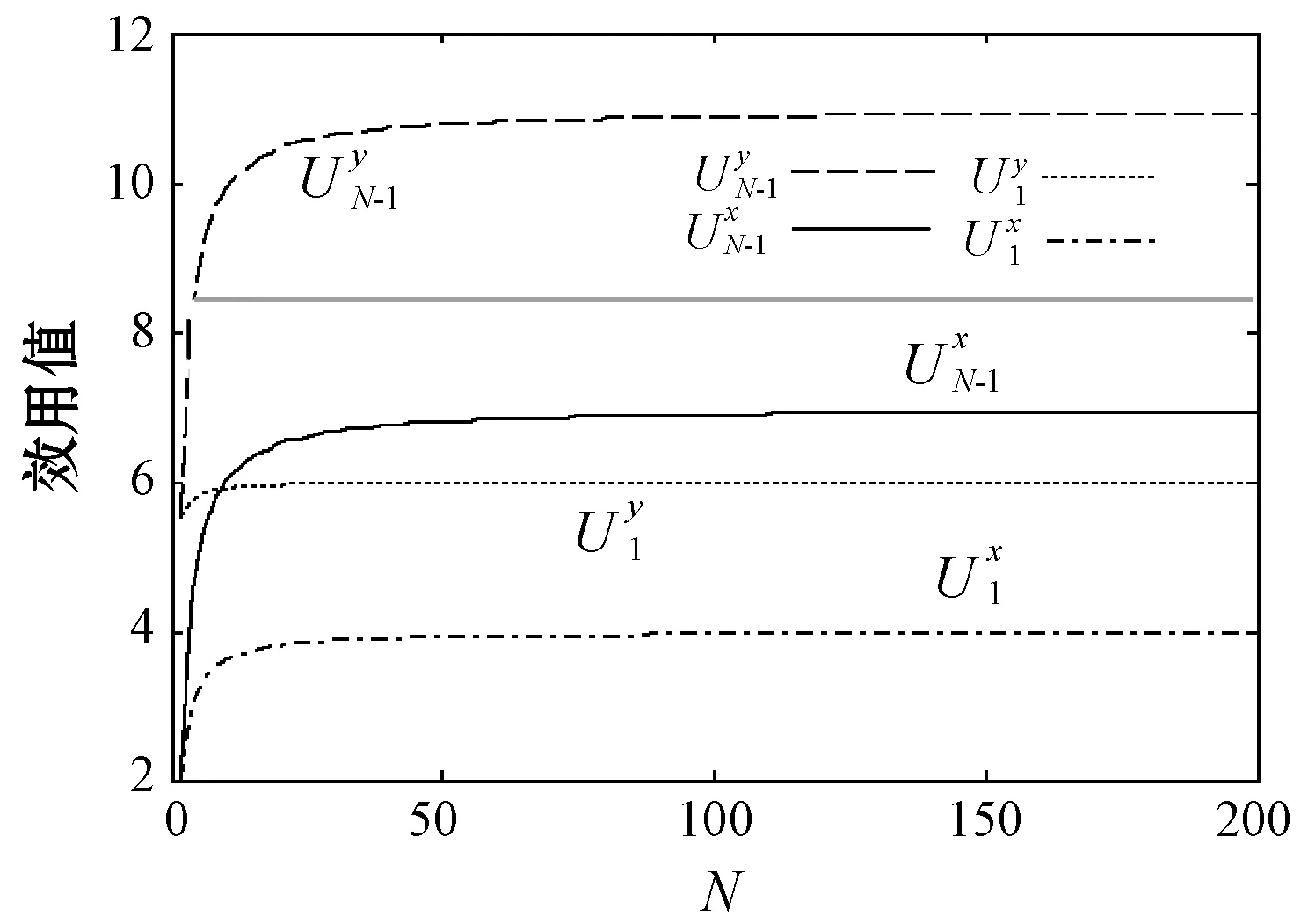
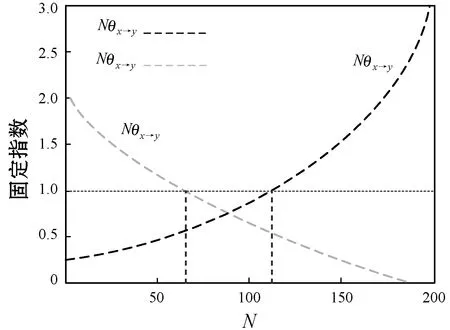
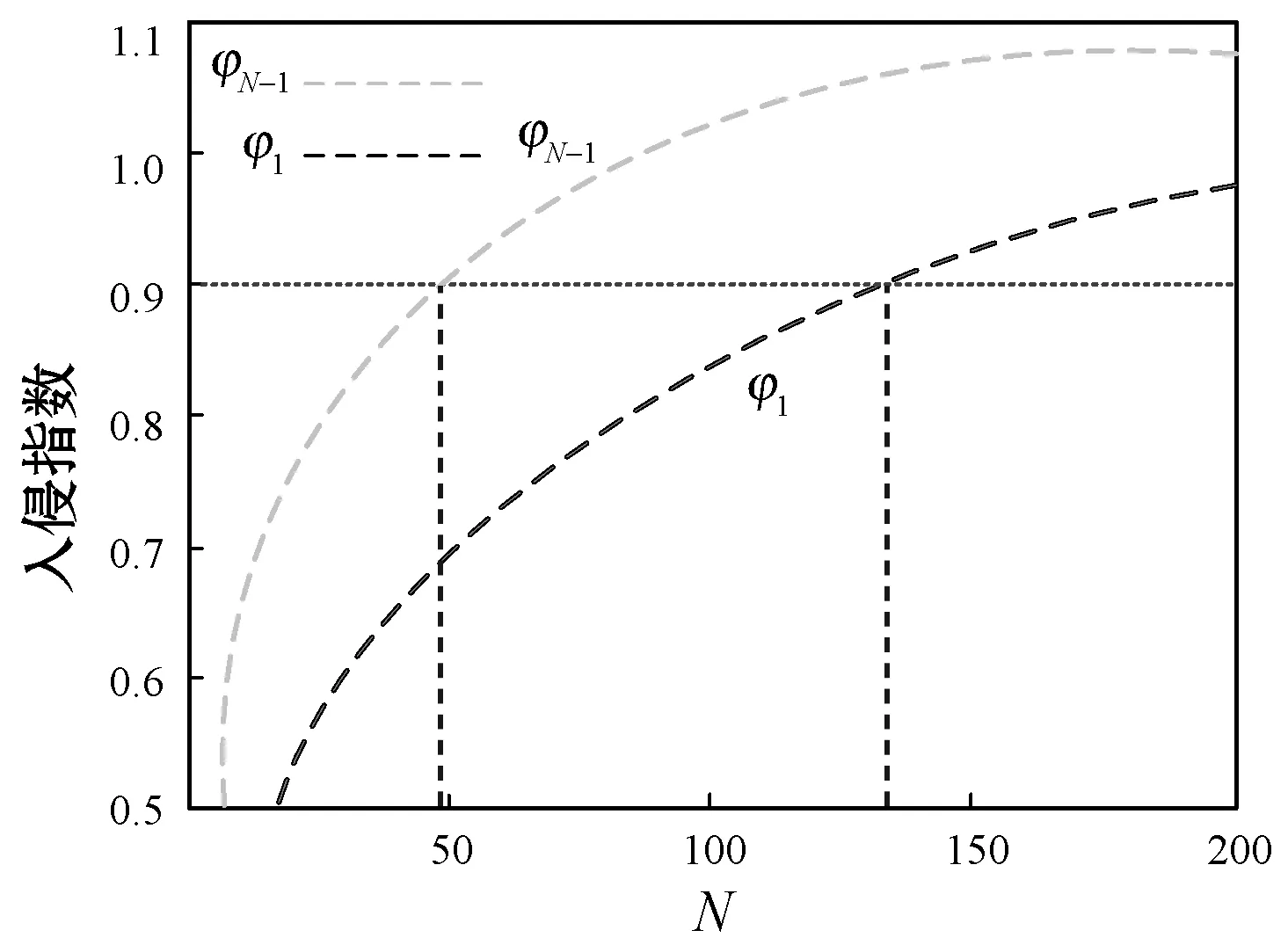
效用矩阵的含义可理解为:当面对另一采用策略x的用户时,用户采用策略x的效用为a,而面对另一采用策略y的用户时,用户采用策略x的效用为c,其他依此类推。两种用户策略x和y定义为竞价ky和竞价y,y为用户预算,k为常数,0 (3) (4) (5) (6) 令px和py分别表示采用策略x和策略y的用户比例,则: px+py=1 (7) 采用x和y的用户效用为: Ux=apx+bpy=apx+b(1-px) (8) Uy=cpx+dpy=cpx+d(1-px) (9) 云用户种群的平均效用为: (10) 效用作为云用户反映其目标和偏好的质量指标,在重复博弈过程中,较优的策略将为用户带来更高的效用,并感染云种群采用较差的策略。 复制方程集合描述了决策选择过程,每种策略的平均增长率为其适应度与整个种群的平均适应度之差得到。 由于px+py=1,可知: (11) 且: Ux-Uy=(a-c)px+(b-d)(1-px) (12) 如图1所示,均衡点或者在边界或者在内部,有以下五种常见情况: 1) 当a>c且b>d时,种群进化最终将由利用策略x的用户组成。唯一稳定均衡点为px=1。策略x为严格Nash均衡,即为进化稳定策略ESS,策略y不是。形态表示为x←y。 2) 当a 5) 当a=c且b=d时,整个种群维持当前状态,策略x和y具有同等偏好。代与代之间的进化不作改变。形态表示为x--y。 图1 不同稳定点的图示 对于有限云种群中的进化博弈,N个个体的策略的选择动态可形式化为带来频率依赖适应度的Moran过程[11]。假设云种群由N个云用户组成,采用策略x的用户数量为i,则采用策略x的用户比例为(N-i)/N,每个采用策略x的用户需与其他们用户博弈。根据式(8),采用策略x的用户效用可定义为: (13) 采用策略y的用户数量为N-i,则根据式(9),该类用户效用为: (14) 令Ti,i+1表示用户数增加一个的概率,Ti,i-1表示用户减少一个的概率,Ti,i表示用户保持不变的概率,则: (15) (16) Ti,i=1-Ti,i+1-Ti,i-1 (17) 转移矩阵为: (18) 式(18)表示云种群的状态变化转移矩阵仅在三条对角线上可以进行转换,其他概率均为0,这是由于相同类型的用户不会增加或减少多于两个。 进化博弈拥有两个吸收态,即i=0和i=N。i=0表示所有云用户采用策略x,i=N表示所有云用户采用策略y。当云种群到达两个状态之一时,这种状态将保持稳定。否则,拥有更高效用的策略将入侵拥有低效用的策略。以下将计算两个状态间的吸收概率。 令ri表示采用策略x的用户数量从i改变为N的概率,即从状态变为状态i=N的概率。ri可表示为递归关系式: ri=Ti,i+1ri+1+Ti,iri+Ti,i-1ri-1 (19) 明显地,ri拥有两个吸收点r0=0和rN=1,其中,r0=0表示当没有用户采用策略x时用户数量从N变为0的概率,rN=1表示当所有用户采用策略x时云种群状态保持稳定的概率。换言之,采用策略y的概率为0。 将式(15)-式(17)代入式(19),则: ri=Ti,i+1ri+1+(1-Ti,i+1-Ti,i-1)ri+Ti,i-1ri-1= Ti,i+1(ri+1-ri)-Ti,i-1(ri-ri-1)+ri⟹ Ti,i+1(ri+1-ri)-Ti,i-1(ri-ri-1)=0 (20) 令wi=ri-ri-1,根据式(13)、式(14)和式(20),则: (21) 将r0=0代入式(21),则: (22) 将rN=1代入式(22),则: (23) 联合式(22)和式(23),有: (24) 根据式(24),定义两种概率θx→y=r1和θy→x=1-rN-1。前者表示种群中一个x用户变化为y用户且固定的概率,后者则反之。定义θx→y和θy→x为两固定指数,当θx→y变大时,选择策略x的用户将逐步入侵整个种群,当θy→x增加时,选择策略x的用户将被其他策略代替,则: (25) 当采用策略x和y的用户拥有相同效用时,称为中立变种,其固定指数为1/N。本文利用1/N作为有限云种群中搜索策略选择动态的基准。显然,如果θx→y>1/N,则策略选择将偏好策略x代替策略y;如果θx→y<1/N,策略选择将反对策略x代替策略y。 定义另一种度量指数,称为入侵指数,表示为: (26) 通过式(26),可以比较每个i下的Uxi和Uyi,评估在位置i上该选择是否增加或减少了策略x的用户数量。联合式(13)和式(14)可知,入侵动态可以φ1和φN-1的形式表示。入侵指数φ1和φN-1可以评估是否采用策略x或y的单个用户拥有比整个种群更大的效用。如果φ1>1,则策略选择偏好策略x入侵策略y;如果φN-1<1,策略选择偏策略y入侵策略x。 从式(24)、式(26)、式(13)和式(14)可以发现,固定指数和入侵指数在其表达上拥有不同的复杂性。入侵指数表达更加简单,为用户效用矩阵和种群N的函数,函数φ1和φN-1用于评估当采用策略x的用户数量为i时是否其用户数量在下一步将增加或减少。然而,固定指数的表达更加复杂,无法明确通过N显示。函数θx→y和θy→x用于度量进化博弈中用户策略保持稳定的概率。 由于固定指数和入侵指数均取决于N,即种群大小对于用户策略的选择动态具有重要影响。实验中将研究固定效用矩阵中N值的改变对选择动态的影响。 本节利用数值实验观察在具体的效用矩阵中不同种群大小N下用户策略的进化方向变化。定义两种评估函数分别为v1i(σi)=4/σi(实验1)和v2i(σi)=4ln(1+σi)(实验2),σi为分配给i的资源分配比例。令k=1/2和y=2,则云用户的竞价策略包括竞价为1和竞价为2。 表2 具有两种策略的博弈效用矩阵 给出效用矩阵后,固定指数和入侵指数仅为种群大小N的函数。图2-图5为MATLAB下的数值分析结果,表示在有限云种群中入侵指数和固定指数的变化情况。图2显示当种群大小增加时,用户效用增加较少,甚至保持不变。图3显示当种群大小很小时,固定指数发生了显著变化。随着种群增加,固定指数趋于平衡。在不同种群规模下量化的数值如图4和图5,具体地: (1) 对于N≤5,φ1,φN-1>1且θx→y<1/N<θy→x,策略选择偏好策略x,且该策略将逐步占据整个种群。 (2) 对于5 (3) 对于8 图2 效用变化 图3 固定指数 图4 表2效用矩阵得到的入侵指数 图5 表2效用矩阵得到的固定指数 表3 两种策略的效用矩阵 对于无限的种群大小,策略x的适应度大于策略y。因此,可以说策略x占优y,这表明策略x为严格Nash均衡或进化稳定策略ESS,而y不是。对于有限的种群大小,可以看出根据N有五种情况。随着N的增加,策略x逐步获得对于y的占优。同时,注意到a+d>b+c,策略选择对于任意N均不会偏好作出改变。而a+b>c+d,对于较大的种群大小,策略选择不会偏好y。如图6和图7所示,有: 图6 表3效用矩阵得到的固定指数 图7 表3效用矩阵得到的入侵指数 本文提出一种随机动态模型,研究了有限云种群环境中的资源分配的进化博弈问题。通过对称的用户2×2效用矩阵,将用户对资源的竞价形式形式化为进化博弈,利用Moran过程寻找重复博弈过程中用户的策略选择在固定指数和入侵指数上的进化动态,求解了用户种群在策略选择上的演化方向。通过两个具体的效用矩阵的数值分析,证明了该博弈算法下用户为了最大化自身效用,其策略选择对于不同的种群大小进化方向是不同的。
3 基于Moran过程的选择动态
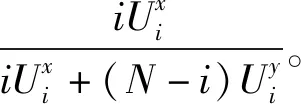
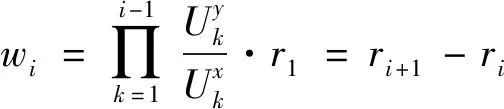
4 有限云种群中的选择动态
5 数值分析
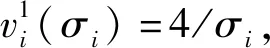




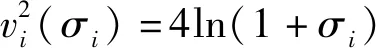

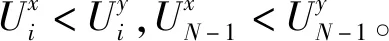




6 结 语

