基于大数据的试井解释参数分析

文必龙 李艳春

(东北石油大学计算机与信息技术学院 黑龙江 大庆 163318)

0 引 言

试井解释是通过检查、分析试井资料的特征获取有关油藏信息和描述油藏物理本性参数的过程[1]。但是现阶段的方法都是以图版拟合为基础，即实测曲线与理论典型曲线相比对得到最佳拟合理论曲线及拟合点，通过反演的方式反求地层参数[2-4]，对于图版的选择需要依靠解释人员经验指导，并且单井解释需通过多组图版进行比对。试井解释智能化的概念在1986年石油国际会议上被格林加登提出，他认为试井解释具有主观推理特性，试井分析问题可归纳为人工智能问题，这推动了人工智能在试井领域中的应用研究[5]，成为现代试井解释的标志。然而，传统的人工智能算法所选用的数据量很小且趋于理想化，随着试井数据采集量扩大，传统的分析方法和人工智能算法的应用逐渐受到限制。因此，现有的试井解释方法至少存在三方面不足：(1) 分析过程具有解释人员主观性使结果不唯一；(2) 图版分析过程繁琐且低效；(3) 专家的经验不能复用。针对以上几点不足，提出基于大数据的试井解释方法，弱化图版拟合的方式，利用多年试井解释中长期积累的海量数据，通过数据驱动的方式结合大数据分析技术，挖掘试井解释历史数据与试井解释结果间的潜在模式，构建试井解释参数预测模型，从而利用压力数据预测得到试井解释结果。对海量历史解释数据进行有效的利用，减少人工参与和经验对解释结果的束缚，使复杂和专业性的试井解释流程精简化。

1 试井解释大数据分析模式

多年试井解释中积累了海量数据，这些数据的潜在价值是真实而巨大的[6]。在试井解释大数据的支持下进行基于大数据的试井解释参数分析，本质是对试井大数据隐含模式的探索并对未来情况的建模[7]，使试井解释从经验驱动转变为数据驱动。本文参照跨行业数据挖掘标准流程CRISP-DM[8]设计了基于大数据的试井解释参数分析流程，如图1所示。

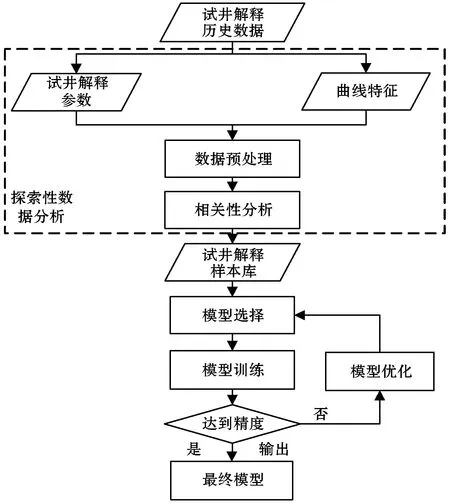
图1 基于大数据的试井解释参数分析流程图

基于大数据的试井解释参数分析流程主要分为以下步骤：

(1) 对试井解释历史数据中的压力导数双对数曲线进行分析，研究压力导数双对数曲线所反映的同类型试井的共性特征，以及曲线特征的描述方法。

(2) 对曲线特征与试井解释参数进行相关性分析，确定模型构建所需的敏感性变量，与试井基础数据构成试井解释样本库。

(3) 通过分析试井解释问题的求解类型，选择合适的建模方法，构建试井解释参数预测模型。

(4) 通过误差分析结果，对模型进行调优，确定试井解释参数的最终模型。以试井解释压力导数双对数曲线数据作为输入对试井解释参数直接进行预测，替代使用图版拟合并通过复杂方程求解的过程。

2 探索性数据分析

2.1 压力导数曲线特征提取

试井解释软件通过计算机匹配拟合误差最小的样板曲线，但是由于只考虑数据总体误差最小化，而没有考虑曲线特征的作用，导致并不能匹配到解释的最佳拟合位置。手动拟合分析用视觉估计实测曲线与样板曲线的拟合误差，往往同一组数据会存在多种解释。而且曲线拟合所用的图版是在某种参数组合的条件下绘制，即使同一类型的油藏实测曲线与理论曲线相比也存在平移、有噪声等问题，二者不能完全统一。本文采用弱化图版拟合的方式，通过实测曲线特征量化试井解释经验，采用特征组合的曲线描述方式，利用曲线特征数据直接进行解释分析。

不同的试井压力导数曲线的总特征不同，但是同一类型的试井压力导数曲线的总特征存在共性，压力导数曲线的早期、中期和晚期特征分别反映井筒、油藏及外边界的情况[9]。传统图版拟合分析也是基于这一特性，最终都需要试井解释专家根据曲线拟合效果更准确地找到样本曲线与拟合位置，其依据是在双对数曲线上，各种不同的油气藏、不同的井类型、不同流动阶段均有不同的特征[10]。描述曲线特征就是试井解释的关键，利用特征组合方式进行曲线特征描述过程如下：

首先，根据试井曲线的特征进行特征点选择，选定一组可以准确表述曲线峰值点和径向流水平线的位置以及两者之间关系的特征点。图2为通过特征点描述曲线的显著特征图。

图2 曲线特征点图

其中：Start_point为压力曲线与导数曲线重合起点；

Cross_point为压力曲线与导数曲线重合的终点；

Top_point为压力导数曲线的早期峰值点；

Radial_point1为压力导数曲线径向流段起点；

Radial_point2为压力导数曲线径向流段起点对应压力值。

在双对数坐标中通过Start_point、Cross_point和Top_point确定压力导数曲线与压差曲线的重合位置和压力导数曲线早期峰值，通过Radial_point1和Radial_point2确定无限大径向流阶段0.5的水平线的位置。

其次，进行特征描述，细化特征点有效信息，确定双对数曲线的形态和位置，如表1所示，通过特征点横、纵坐标，时间比例，曲线构成面积等一系列属性值来描述特征点与其临近区域的相互关系。

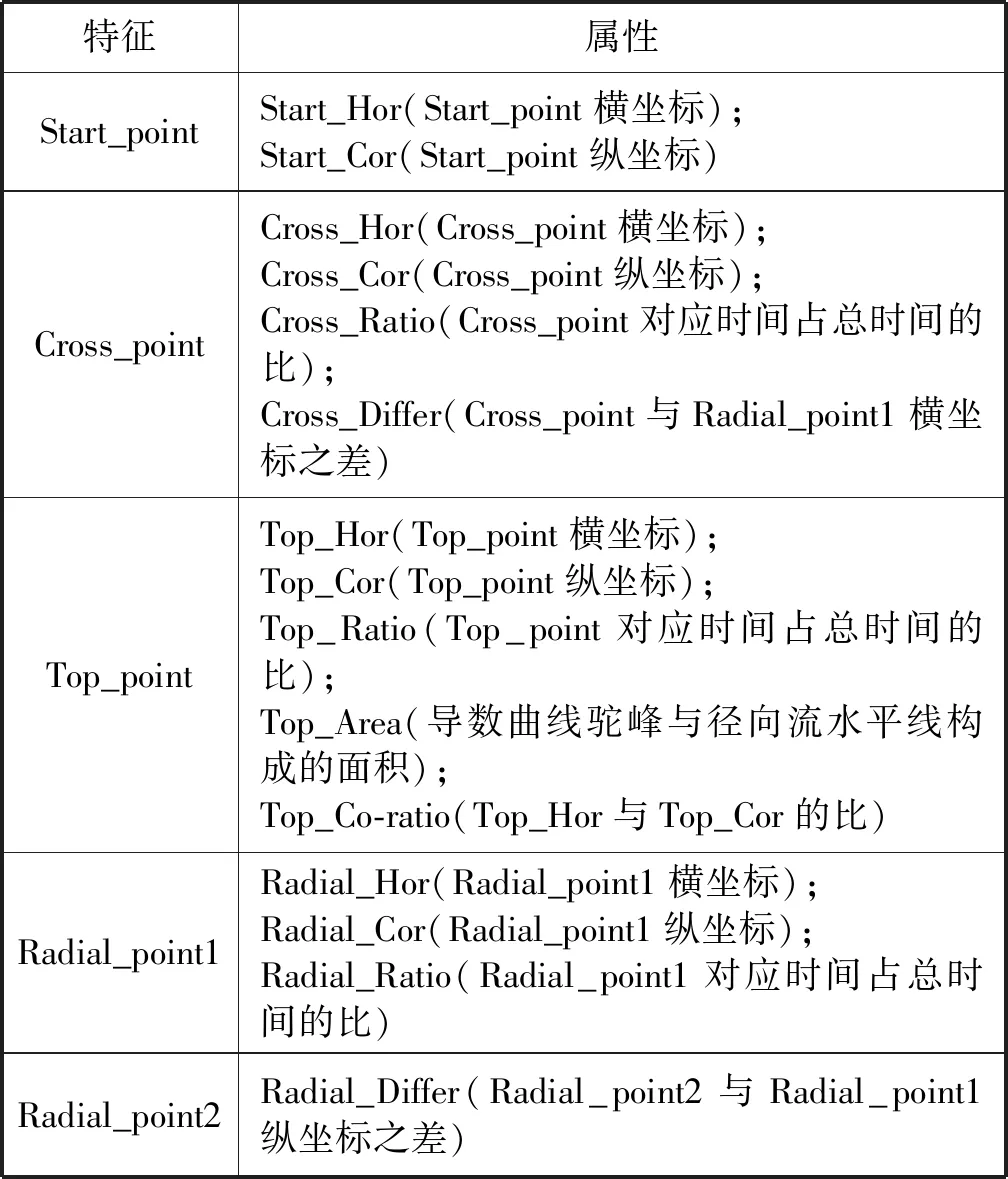
表1 曲线特征属性表

最后，以分析均质油藏的井筒储集系数、流动系数和表皮系数三个试井解释参数为例，利用曲线特征和解释参数共同构成分析数据集。

2.2 数据预处理

基于大数据的试井解释参数分析所需的信息全靠从数据中得来，但在压力测试过程中会受到实际客观条件和人为主观条件的限制，导致测试数据出现不确定的测试偏差，这些偏差会直接影响试井解释建模效果的好坏，因此在开始分析处理之前必须要对分析数据集进行修正。通过数据预处理改进数据的质量，使后面的分析结果和解释模型更可靠。

对缺失数据的处理先探寻缺失值的来源，类似试井解释基本数据井径，油藏数据孔隙度、粘度这种特定不可替换的数据缺失，为不影响计算应采用剔除的方式；类似试井压力数据这种连续型数据的缺失可以采用插值方式进行数据修正。

对于异常值的处理，其被视为异常的原因不同,在不明确数据集分布情况下可采用箱线图来检测异常值。箱线图可清晰地显示一组数据的分散情况，并提供识别异常值的一个标准：异常值被定义为小于Q1-1.5IQR或大于Q3+1.5IQR的值(Q1、Q3为上下四分位数，IQR为四分位距)[11]。图3为利用箱线图处理井筒储集系数异常值的检验结果。图3(a)中位于两侧虚线外侧的均为异常值，对应的样本数量稀少，应予以剔除，剔除后如图3(b)，数据无异常值存在。

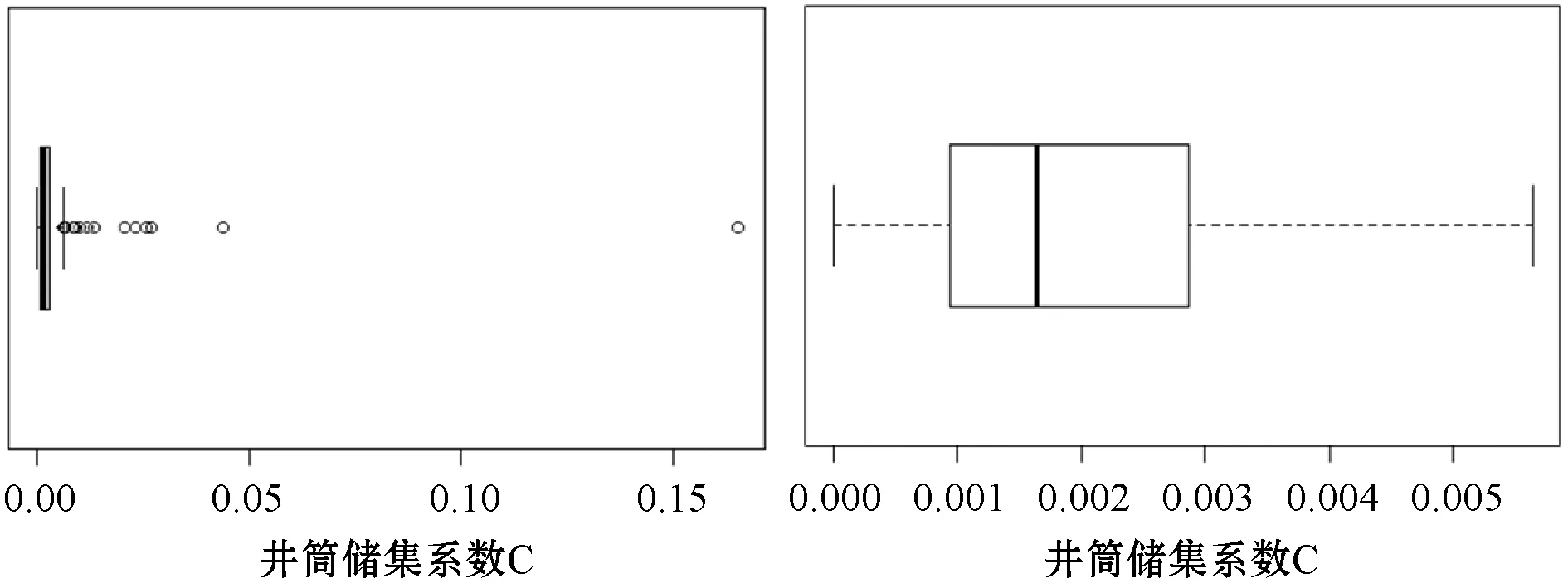
(a) 箱线图-处理前 (b) 箱线图-处理后图3 井筒储集系数异常值检测

数据预处理后，对试井解释结果原始数据进行K-S检验，验证是否符合正态分布。如果检验P值大于0.05，则表明K-S检验的原假设成立，即原数据符合正态分布；若P值小于0.05，则不符合正态分布。以井筒储集系数为例进行分布检验，其P值为0.131，可以认为服从正态分布。且预处理前井筒储集系数的峰度和偏度分别为822.52和27.67，样本进行预处理后其峰度和偏度分别为0.16和0.91，均小于1，说明样本数据符合正态分布，如图4所示为预处理前后分布情况对比。

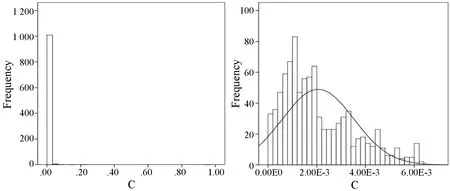
(a) (b)图4 解释参数分布情况对比图

2.3 相关性分析

在基于大数据的试井解释参数分析中更加关注数据总体，从数据的总体中可以直接获取有价值的信息，大数据相关分析是大数据分析中对有价值信息挖掘的关键，曲线特征描述过多会导致信息冗余和模型的可解释性降低，通过相关性分析能有效地发现与度量曲线特征与试井解释结果之间的相关关系[12]。通过相关性分析来确定试井解释参数预测中的敏感性变量，对整体的数据集合进行多变量的关联性分析，从特征样本库的众多输入指标(不含解释结果)，找出影响解释结果参数(如流动系数、井筒存储系数和表皮系数)的特征，将这些特征作为分析的实际特征，构建试井解释样本库。

对预处理后得到的数据进行相关性分析，计算任意解释参数与曲线特征之间的相关系数，度量此类数据相关性本节采用积距相关系数进行计算，计算公式如下：

(1)

式中：X和Y分别为解释参数和曲线特征。

其样本相关系数为：

(2)

由式(2)计算出解释参数与曲线特征之间相关系数，通过表2所示的相关系数表衡量两者之间的相关关系，相关系数越大则认为曲线特征对解释参数的影响越大，将表中相关系数较大的特征选进试井解释样本库中，用于最终预测模型的建立。

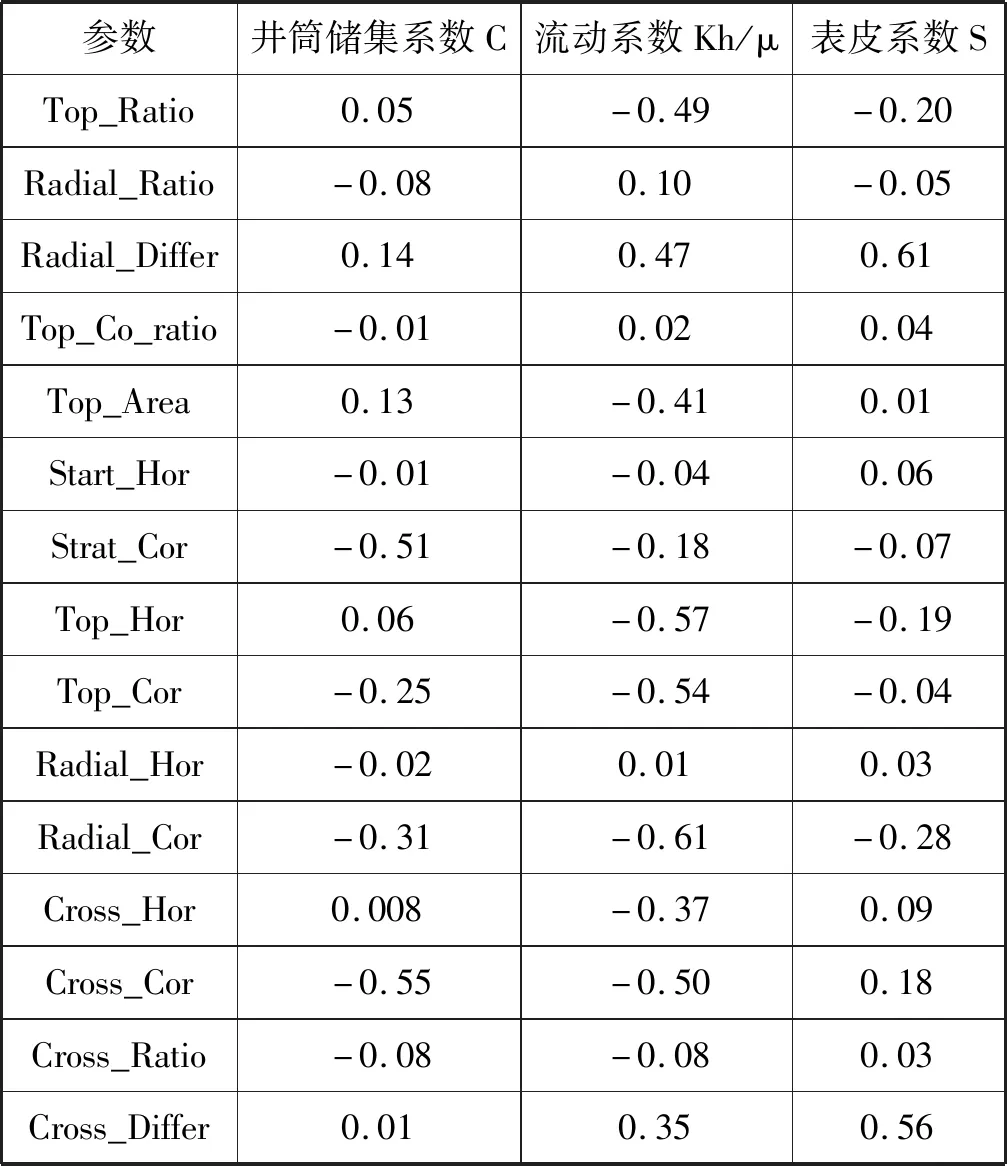
表2 解释参数相关系数表

为更直观地表述两者的相关关系，绘制如图5所示的相关性矩阵，当曲线特征与解释参数相关性矩阵中被观察变量之间存在相关关系时，数据点会呈现一个集中趋势[13]。

图5 曲线特征与解释参数相关性矩阵图

通过表2相关系数和图5相关性矩阵分析比较变量之间的相关性，可以发现井筒储集系数受Strat_Cor和Cross_Cor的动态影响；流动系数受Top_Hor、Top_Cor、Radial_Cor和Cross_Cor的动态影响；表皮系数受Radial_Differ和Cross_Differ的动态影响。这说明井筒储集系数与压力导数双对数曲线的早期形态有关，流动系数与压力导数曲线驼峰出现的时间以及峰值点的位置有关，表皮系数与两条曲线开口大小(即纵坐标差值)有关，以此筛选出特征数据集作为模型的输入集符合正态分布。

3 试井解释大数据分析模型

3.1 模型构建

不同类型的试井存在总体特征相同，具体存在差异的问题，所以试井解释参数的预测方法需要有很强的适应性，而神经网络具有函数逼近能力，能自动逼近学习范围内的任意插值情况[14]，故使用神经网络方法来建立基于大数据的试井解释参数预测模型。通过相关性分析对曲线特征数据进行有效降维，保留与各解释参数有很大关联度的敏感性变量，作为神经网络模型构建的输入变量，从而构建试井解释参数预测模型。

模型的具体设定如下：

(1) 输入层：输入层节点对应于模型的输入变量，本模型中输入节点由曲线特征变量决定。

(2) 输出层：输出层节点对应预测目标，本模型中输出节点由试井解释参数决定，本文中只讨论井筒储集系数、流动系数和表皮系数三个试井解释参数，故输出层节点数为3。

(3) 隐含层：隐含层的神经元数太少，网络不能很好地学习，需要训练的次数较多，精度也不高;神经元数太多，则导致训练时间较长，甚至不收敛。经过多次调试实验，隐含层数目为10时，神经网络对函数的逼近效果最好。

(4) 样本选择：预测模型的样本数据为某地区均质油藏的Gringarten-Bourdet图版的历史试井解释数据，尽管学习样本不可能覆盖所有可能的参数值，但神经网络具有自适应性，实测曲线特征和解释参数的度量在学习范围内，不管学习样本是否与之完全吻合，模型都能给出预测值[15]。

(5) 模型验证：采用保持样本的方法对预测模型进行验证，把学习样本划分为训练集和检验集，以训练集进行模型训练，以检验集进行正确率评估。

3.2 模型优化

为提高模型预测精度，对特征数据集进一步采取双变量分析。以分析Kh/μ(流动系数)与Radial_Cor为例进行双变量分析，如图6(a)所示，Kh/μ与Radial_Cor存在相关性，但两者之间的相关关系呈现出多条趋势线。进一步探究分析发现呈现多条趋势线是由于数据来源于不同井造成的，试井解释参数模型是通过数据的共性特征构建通用模型，可通过特征工程对模型的输入输出进行变量转换。通过下式可以发现拟合值pm是与单井信息无关的变量，采用预测pm代替Kh/μ消除数据来源于不同井对预测的影响，提高模型的预测精度。

(3)

图6(a)和图6(b)分别是Kh/μ和pm与Radial_Cor相关性分析图，显然进行特征变换后变量间相关性明显增强。对其他两个参数也采用相同的方法进行处理，由于弱化图版的概念对时间拟合值、压力拟合值以及曲线参数cDe2s只作为一个拟合值的数据集，分别表示为tm、pm和cm。通过预测拟合值间接预测解释参数，分析数据源由曲线特征数据集与试井解释结果变为曲线特征数据集与拟合值数据集，进而通过拟合值的预测结果求得试井解释参数。

(a) (b)图6 曲线特征与解释参数双变量分析图

对于不能直接通过变量替换解决的问题，可以通过特征工程进行新变量和新特征的创造，井筒储集系数C与tm、pm两个拟合值都存在联系，需通过tm、pm两个拟合值提取一个间接拟合值pm/tm，记为pm_tm来替代C，并构建新特征值Radial_Top(通过Top_Hor与Radial_Cor拟合得到)。C的表达式如下：

(4)

对特征数据集与拟合值数据集的分析得到表3相关系数表，重新构建模型的网络结构，并对模型进行训练，从而得到最终的试井解释参数预测模型。

表3 拟合值相关系数表

3.3 模型评估

采用前文提到的保持样本的方法模型进行验证，通过训练后的试井解释参数预测模型对测试样本进行预测，如图7(a)所示，星号为表皮系数预测输出值(预测值)，圆圈为表皮系数期望输出值(实际值)，预测值在实际值上下浮动，基本与实际值重合。由图7(b)可知，测试样本预测误差均分布在[-1，1]之间，大部分集中于[-0.5，0.5]，偏离零点线程度不大，故该模型的预测误差在一个可以接受的范围内，说明模型预测效果比较好。

(a) (b)图7 模型表皮系数(S)预测值与期望值误差和对比

由图8可以看出，训练样本和测试样本中表皮系数预测值和实际值的数据点拟合效果较好，集中于拟合线y=x附近，说明模型训练和测试性能较好且稳定。由表4可知模型其他试井解释参数的预测情况，表皮系数的训练样本预测值和实际值相关系数为0.978 9，测试样本预测值和实际值的相关系数为0.975 3；井筒储集系数的训练样本预测值和实际值相关系数为0.977 3，测试样本预测值和实际值的相关系数为0.976 8；流动系数的训练样本预测值和实际值相关系数为0.983 4，测试样本预测值和实际值的相关系数为0.990 4，相关系数均处于稳定，说明模型泛化能力较佳。

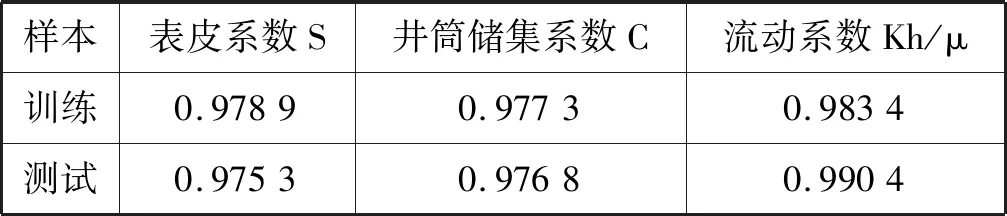
表4 模型训练和测试的预测值和实际值的相关系数

4 实例分析

利用本文所训练的模型对历史试井数据进行分析,并与传统试井解释方法进行对比。

4.1 基础数据

生产时间为91.75 h，常产量为2.17 m3/d，原油体积系数为1.198，综合压缩系数为0.145 9×10-4MPa-1，油层厚度为3 m，测试井半径为0.069 85 m，原油黏度为0.8 mPa·s，孔隙度为0.222。实测记录的压力及压力导数双对数曲线见图9。

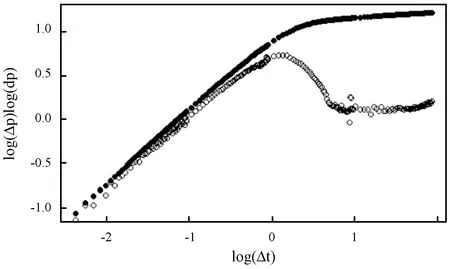
图9 实测记录的压力及压力导数双对数曲线图

4.2 结果比对

原解释结果：流动系数为0.711 0-3μm2.m/mPa.s；井筒存储为0.002 5 m3/Mpa；表皮系数为2.01；神经网络模型计算解释结果：流动系数为0.701 0-3μm2.m/mPa.s；井筒存储为0.002 7m3/Mpa;表皮系数为1.73。预测结果与原解释结果相吻合，证明了基于大数据的试井解释参数分析方法的可靠性，且解释流程更加精简化，避免了图版拟合的固有误差和解释人员主观性对解释结果的影响。

5 结 语

本文提出的方法运用大数据分析，以试井解释分析的历史数据为依据，深挖压力导数双对数曲线与试井解释参数的关联关系，提出曲线特征的描述方法量化同类型试井的共性特征，采用相关分析确定与试井解释参数相关的独立变量，进而通过神经网络辅助进行模型构建。利用神经网络的函数逼近能力，克服了传统图版只能包含部分典型曲线的局限性，消除了传统图版分析的固有误差，以弱化图版拟合的方式减少人工参与对拟合结果的束缚，使试井解释过程更简捷。利用此方法，解决单井解释需要多组典型曲线图版的不足，消除传统方法的复杂性及多解性，一次解释确定所有参数。

本文研究的虽然是用于均质无限大油藏图版拟合分析的Gringarten-Bourdet图版的解释结果，但方法可以很容易地进行推广，其意义不仅在于实现这一类问题的分析智能化，更在于为试井解释提供了智能分析新方法，结束需要多组图版联合分析的历史。