不同GNSS星载原子钟周期特性分析

孙 广, 朱翔宇, 李双钦, 郭美军, 翟 伟, 洪英杰

(西安航天天绘数据技术有限公司，西安 710100)

0 引言

目前，卫星钟差以及轨道的精度，在一定程度上决定了全球导航卫星系统(Global Navigation Satellite System，GNSS)的服务精度，当轨道平稳变化时，轨道预报精度可支持实时精密定位，但卫星的钟差精度较低。此外，星载原子钟作为星上的时间基准，其性能很大程度决定了导航、定位和授时的精度[1-2]。大量时间累积的卫星钟差数据，可以分析评估星载原子钟的健康状态。GNSS的完好性[3]、系统性能评估[4]和GNSS卫星钟差计算[5]及预报[6-7]等领域都是当前研究的热点。同时，很多专业人员对GNSS星载原子钟周期项计算以及钟差改正评估都有一定的研究[2,7]。针对中国北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)原子钟周期的研究成果较少。

我国的BDS，将在2020年实现全球覆盖；而俄罗斯的GLONASS已经是全球覆盖，欧洲的Galileo系统也正在逐步发展。针对BDS星载原子钟的性能分析[8]采用修正阿伦方差计算，对BDS的倾斜地球同步轨道(Inclined Geosynchronous Satellite Orbit，IGSO)和地球静止轨道(Geostationary Earth Orbit，GEO)星载原子钟的稳定性进行计算分析[9]；有研究人员对BDS卫星钟差数据的周期进行了分析[10]。通常钟差序列包含线性、二次曲线以及周期性变化规律。研究人员基本利用太阳轨道和卫星轨道2个轨道面间的夹角，加入地影期相关系数的变化对钟差的周期性进行改正分析[11]。大量的周期性研究主要集中在全球定位系统(Global Positioning System，GPS)，其他系统钟性能的研究较少。基于此，本文通过2016年的全年多星定轨联合解算的卫星钟差数据，研究分析了BDS、GPS钟差周期特性指标，为后续钟差模型构建提供参考。

1 算法原理

1.1 钟差数据预处理

星载原子钟长时间在轨运行，累计产生误差，很多不确定的因素会对钟差数据产生影响，所以钟差数据中经常会有大的粗差数据、缺失以及异常数据。因此，需要对卫星钟差数据进行去粗差及异常处理。对于大量时间累积的卫星钟差数据相应的频率数据，本文采用抗差较好的中位数法(Median Absolute Deviation，MAD)[12-13]进行粗差去除，如式(1)所示。

|yi|>(m+n·MAD)

(1)

利用式(1)进行粗差判断，并提出，式中，m=Median(yi),MAD= Median{|yi-m|/0.6745}。MAD算法的数据源是频率数据，用钟差数据做差分计算频率数据，然后利用该方法进行粗差去除。对于去除数据的点，一般进行内插替换该点数据或取0。上述处理方法会在原始数据中加入新数据。为了避免引入新数据，本文对异常钟差数据设为空，表示该历元钟差数据缺失。

1.2 星载原子钟钟差模型

星载原子钟在长时间运行会发生一定的频率漂移，所以，构建钟差模型的参数包含卫星钟时频特性的相位、频率、频率漂移的二次多项式模型。构建的模型如式(2)。

Δti=a0+a1(ti-t0)+a2(ti-t0)2+Δi

(2)

式中，i=1,2,…,n，Δti表示第i历元的卫星钟差；t0表示星钟的参考时刻；ti是对应的历元时刻；需要估计的参数a0、a1和a2，对应为t0的相位、频率及频率漂移率；Δi表示原子钟观测误差。需要钟差数据大于3个，可利用式(2)进行估计参数计算。

1.3 星载原子钟的周期项计算

本文利用傅里叶变换对拟合残差序列进行频谱分析。在进行卫星钟差周期项计算时，需要利用二次多项式对卫星钟差进行拟合，可消除钟差趋势项，即可获得拟合残差。然后利用拟合残差进行周期项的计算。离散傅里叶变换(Discrete Fourier Transform，DFT)，其表达式为

(3)

式中，X(k)表示k时段对应的频谱值；X(n)表示相应的拟合残差序列；n表示残差序列中的序号；N是残差的个数，利用该式计算时，需要满足N=2L，L=0,1,2,…,n的条件，若N不满足要求，则进行补0；然后即可求出残差序列中各点的频谱值。在实际仿真计算过程中，采用快速傅里叶变换 (Fast Fourier Transform，FFT)进行求解。然后，根据残差序列的频谱图即可进行周期项提取。

1.4 周期项特性分析

首先，利用多星联合解算的GNSS精密卫星钟差数据进行预处理消除粗差，然后进行二次多项式拟合，再通过拟合数据和原始数据做差得到拟合残差数据，对该数据进行频谱分析可以获得GNSS星载原子钟的周期项。图1给出了本文分析GNSS星载原子钟周期特性的整个流程。

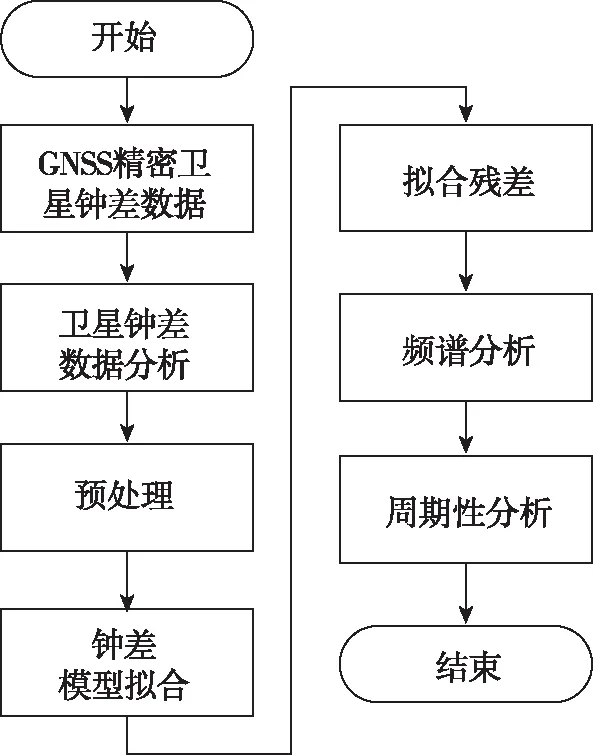
图1 GNSS原子钟周期性分析流程Fig.1 Flow of GNSS atomic clock periodic analysis

2 实验结果分析

本文采用2016年全年的多星定轨联合解算的BDS、GPS卫星钟差数据，进行数据预处理粗差剔除，采用钟差二次多项式模型对卫星钟差数据进行逐天拟合，最终得到相应的拟合残差。利用该拟合残差，对BDS、GPS的周期特性进行分析。实验统计结果中C代表BDS，G代表GPS。

2.1 BDS原子钟周期项频谱分析

利用BDS的拟合残差数据对BDS原子钟周期特性进行了实验分析。对BDS所有的卫星进行了频谱分析，本文以中地球轨道(Medium Earth Orbit，MEO)、GEO、IGSO三种卫星钟的一种为例，进行频谱分析。频谱分析结果如图2～图4所示。

从图2～图4分析可知，BDS的GEO卫星C02星的主周期项在24h、12h以及8h附近时，周期性明显；图3中，IGSO卫星C07的周期项也分布明显，基本与C02主周期项相同，24h的周期与GEO、IGSO卫星轨道周期23h56min基本符合；而MEO类型的C11星的主周期项在12.8h左右，也与MEO卫星轨道周期12h53min基本一致。BDS所有卫星钟主周期项分析统计结果如表1所示。

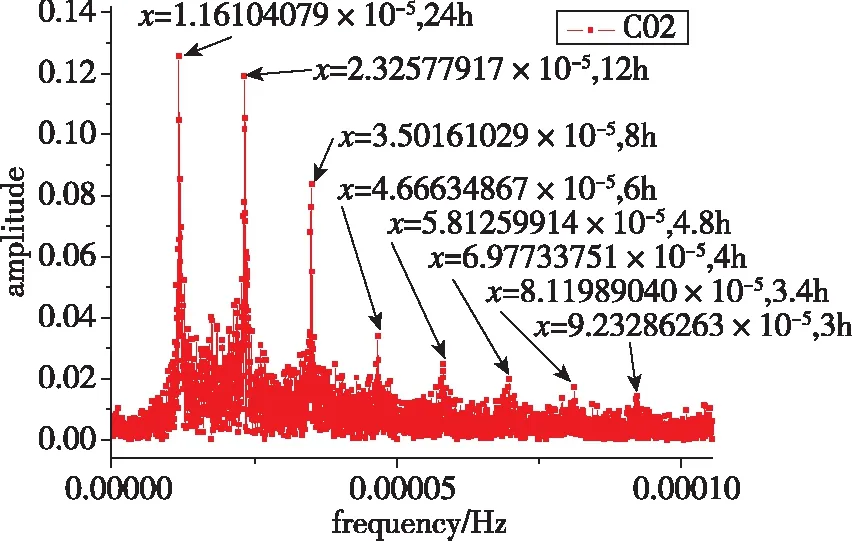
图2 BDS-C02星的钟差数据频谱分析结果 Fig.2 Spectral analysis based on BDS-C02 satellite clock bias

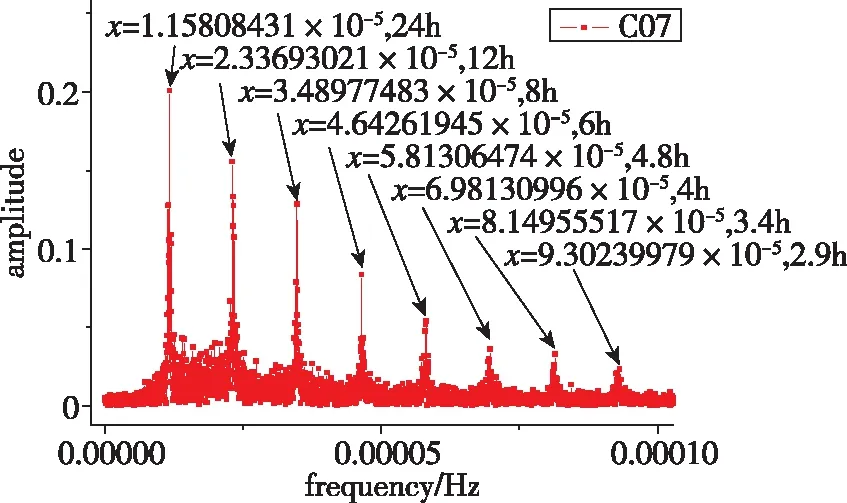
图3 BDS-C07星的钟差数据频谱分析结果Fig.3 Spectral analysis based on BDS-C07 satellite clock bias

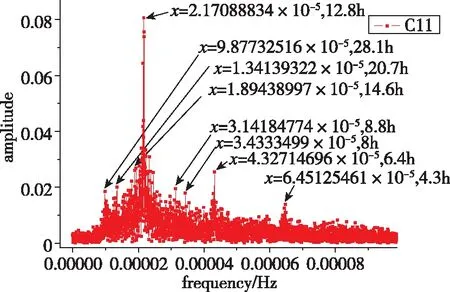
图4 BDS-C11星的钟差数据频谱分析结果Fig.4 Spectral analysis based on BDS-C11 satellite clock bias

h

从表1中可以看出，GEO、IGSO卫星主周期项基本为12h或24h；MEO主周期项为12.8h或6.4h，所有卫星的主周期项基本为轨道周期的1倍或1/2倍。

表1中，GEO、IGSO钟差均含有24h主周期项，而MEO卫星钟差的主周期项则包含相对较长的周期项20.2h、28.1h，这些周期项基本接近24h，可以推断，可能是由于光压模型摄动力对MEO卫星的周期项产生的影响造成的。

2.2 GPS原子钟周期项频谱分析

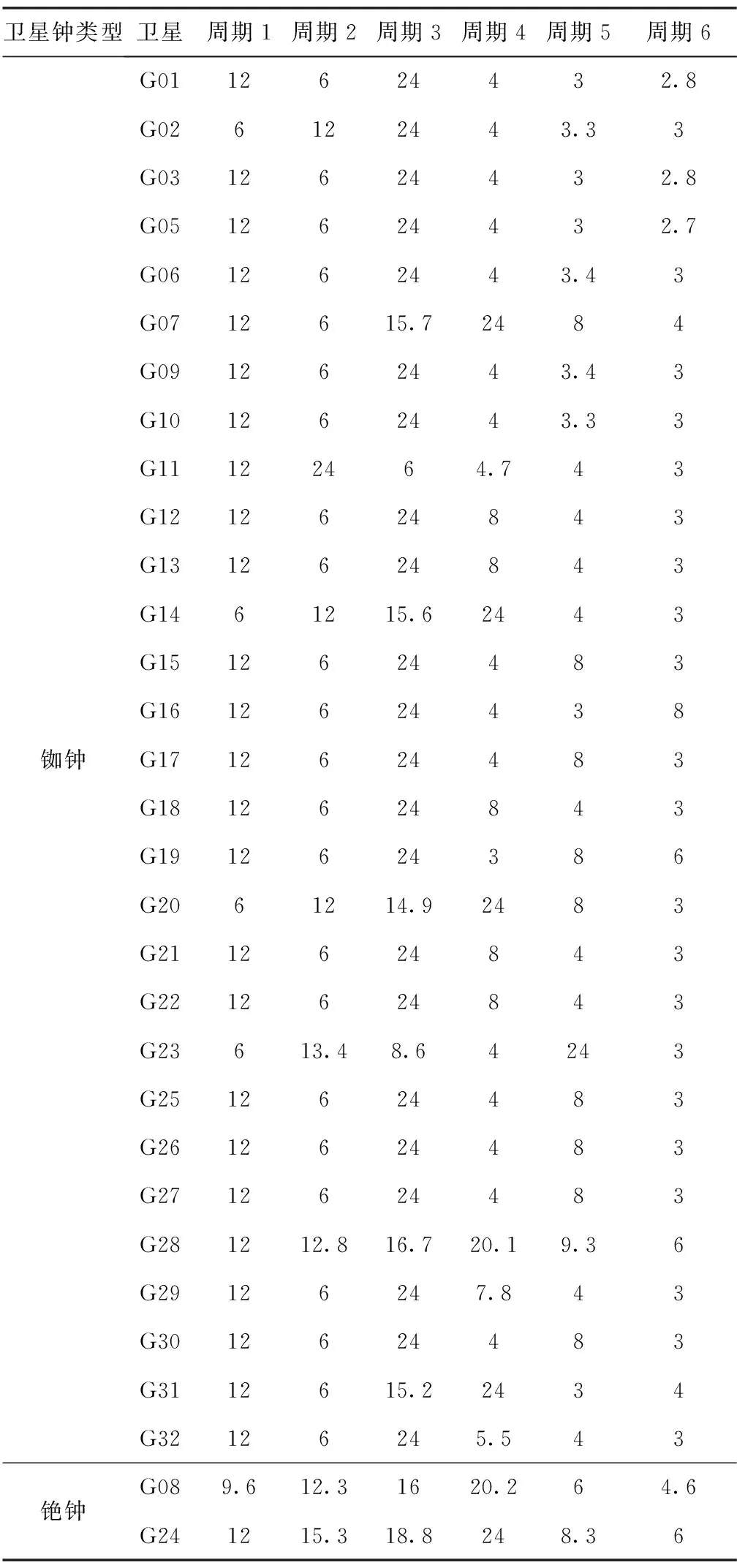
利用GPS的拟合残差数据对GPS原子钟周期特性进行了实验分析。以钟类型为例，分别给出了G06、G08、G30这3颗卫星钟的频谱分析图，其中，G08卫星钟为铯钟，其他2颗卫星钟为铷钟。频谱分析结果如图5～图7所示。

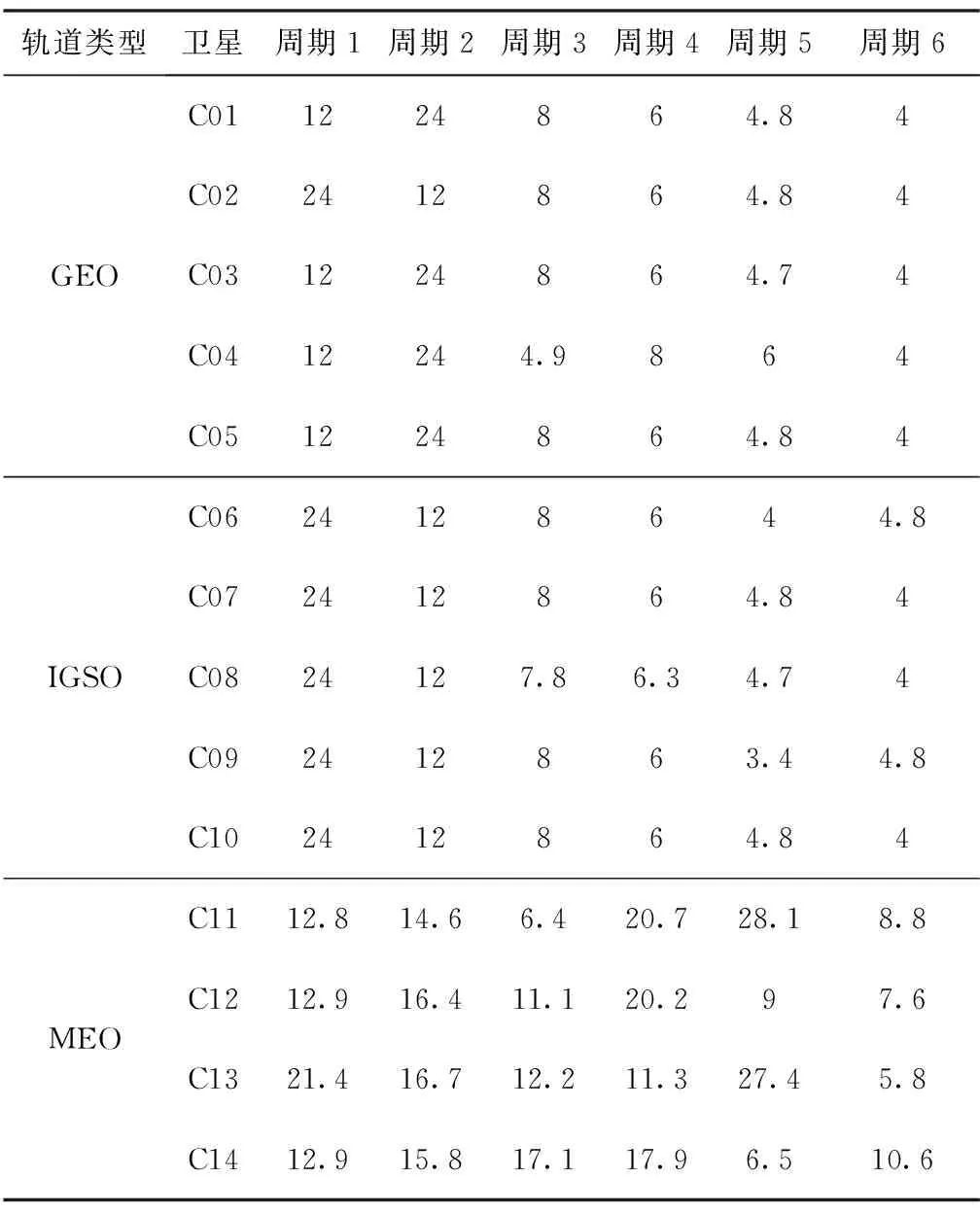
从图5～图7中可以看出，GPS卫星的主周期项为12h、6h、24h，与GPS卫星轨道周期11h58min保持一致，卫星钟差数据的主周期基本为卫星轨道周期的1倍、1/2或2倍。铷钟主周期项分布较为明显，而铯钟各周期项分布规律不清，主要周期项基本在12h附近。GPS卫星的主周期项统计分析结果如表2所示。本文只给出了前6个主周期项，结果表明，GPS卫星钟的周期项与钟的类型有关。

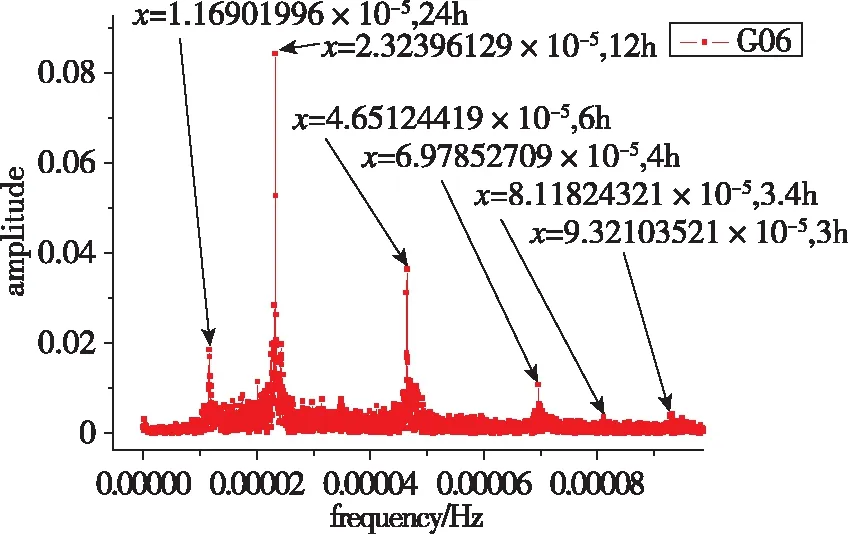
图5 GPS-G06星的钟差数据频谱分析结果Fig.5 Spectral analysis results based on GPS-G06 satellite clock bias

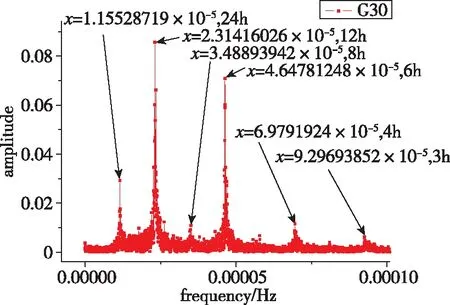
图6 GPS-G30星的钟差数据频谱分析结果Fig.6 Spectral analysis results based on GPS-G30 satellite clock bias

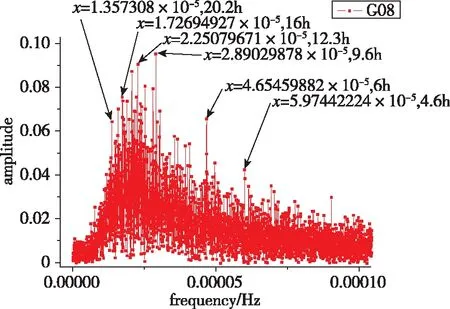
图7 GPS-G08星的钟差数据频谱分析结果Fig.7 Spectral analysis results based on GPS-G08 satellite clock bias

h

从表2中可以看出，G08为铯钟，周期性不好。G06和G30对应的主周期略有不同，这主要是由于不同时期的不同卫星轨道周期略有差异，星载钟的主周期项与卫星轨道周期基本为1倍、1/2或2倍关系。在解算过程中，不同算法对周期也有一定影响，但都在12h附近。由于钟差本身存在一定的误差，拟合后得到的钟差数据也会存在一定的误差，频谱分析得到的钟差周期与GPS卫星的轨道周期近似一致。

3 结论

本文介绍了星载原子钟周期项的提取过程，分析了2016年全年的BDS、GPS主周期项，最终的统计结果表明，BDS、GPS卫星钟除了铷钟存在明显的周期项，铯钟周期项不明显。BDS、GPS的主周期项基本在12h、24h、6h左右。通过本文的试验分析，对BDS、GPS的周期项可得如下结论：

1)轨道类型不同会影响卫星钟差周期项，GEO、IGSO原子钟周期性较为明显，而相同轨道类型的卫星其钟差周期项也有轻微差异；

2)卫星的钟差主周期项，分别为对应卫星轨道周期的1/2或1倍左右；

3)不同类型原子钟的卫星钟差周期项也不同。