基于CS-LBP的散斑应变测量技术*

董庆丰， 肖世德， 李 磊， 李兴坤

(西南交通大学 机械工程学院 四川 成都 610031)

0 引 言

数字图像相关(digital image correlation,DIC)法是一种应用于测量物体面内位移的可靠光学测量方法,具有非接触式、全场应变、简单高效等优点[1～3],已广泛应用于立体匹配、高温变形、断裂分析、材料特性表达和微电子可靠性评估等领域[4]。

DIC方法通过处理物体变形前、后的表面散斑图像来获取物体变形信息[5]。DIC中子区匹配算法的选择是关键问题[6],传统的DIC匹配算法常采用N-R迭代法、粗细搜索法来查找相似度最高的子区[7]。在实际应用中,测量系统难以保证试件变形前后光照强度的一致性。利用传统算法匹配时,光照强度的变化引起变形前后图像灰度值的整体变化,模板子区与目标子区的相关度降低,导致测量精度的下降。

针对传统DIC方法测量精度在光照强度变化时测量精度下降的问题,提出基于CS-LBP的数字图像相关法。在试件表面出现光照变化时,选定变形前图像子区作为模板子区,提取模板子区CS-LBP直方图,利用主成分分析法对直方图进行降维,以之作为匹配参数,查找目标图像中匹配度最高的目标子区,并结合曲面拟合法计算亚像素位移,实现变形的测量。实验结果表明,在光照强度变化小于5 000 lx的情况下,改进算法的误差增幅相较于传统DIC方法降低了42.8 %。

1 DIC的基本原理

对于物体表面区域变形的测量,可以通过研究变形前后两幅散斑图对应点或区域来完成。单个像素点仅包含灰度值信息,依据灰度值信息无法准确找到对应点,以参考点为中心的子区能提供更多参考信息。DIC方法匹配的任务是寻找变形前后两幅散斑图像的对应区域。在变形前图像中,以点P(x0,y0) 为中心,选取像素大小为(2M+1)×(2M+1)的子区作为参考子区,在变形后的图像中查找与参考子区相关性最大的目标子区。对比参考子区与目标子区的变形参数,得到物体表面区域的变形信息。DIC方法示意图如图1。

图1 DIC方法示意

传统DIC方法常选取归一化最小平方距离相关函数(normalized least square distance correlation function,ZNSSD)来计算区域相关系数,即

CZNSSD(p)=

(1)

式中w为所选子区的像素数,F(x,y),G(x′,y′)为变形前图像与变形后图像的灰度值,Fm,Gm为两图像子区的平均灰度值。

2 基于CS-LBP的数字图像相关法

为了解决传统DIC方法因光照变化而导致测量精度下降的问题,提出基于CS-LBP的数字图像相关法。提取图像局部纹理特征,将局部纹理特征作为匹配信息。算法流程如图2所示。

图2 算法流程

2.1 局部二值模式描述

局部二值模式(local binary pattern,LBP)是描述图像局部特征的非参数算子,能高效地描述纹理[8],常用来描述和提取图像的局部特征[9]。

传统的LBP算子的描述对象为一个3×3的正方形窗口,以该窗口中心点的灰度为阈值,对周围的8个领域进行二值化。即如果相邻像素点的灰度值大于或等于中心点灰度值,将其置1,反之置0。以顺时针方向连接得到一个8位二进制LBP编码值。灰度值的整体变化不影响相邻像素点间的大小关系,因此,该二进制LBP编码值具有对光照整体变化的不变性。将二进制值转化为十进制,并将其赋值给中心点的灰度值,逐行扫描整幅图像,进而得到整幅图像的LBP描述。传统LBP算子描述过程如图3。

图3 LBP描述

(2)

式中S(x)为相邻像素的大小关系。

(3)

传统LBP描述没有关注到所选领域内的梯度变化,同时,维数过高的缺点导致其对于图像中的噪声过于敏感。为了利用领域内的梯度变化信息,同时降低LBP描述的维度,引入一种中心对称的CS-LBP算法。设定半径R和采样点数N,依据大小关系,将具有对称关系的像素点对进行二值化。相较于传统的LBP描述,CS-LBP降低了维数,加快了计算的效率并提高了对平坦区域的鲁棒性。传统LBP与CS-LBP描述比较如图4。

图4 LBP描述与CS-LBP描述比较

(4)

式中S(x)为相邻像素的大小关系,R为领域半径,N为像素个数。

2.2 直方图匹配

变形前后的两幅图像经过LBP描述运算后,得到LBP图像。再设定灰度值区间,统计不同灰度值区间的像素点个数,得到散斑图的LBP直方图。

对整个子区生成一个直方图,局部的差异信息未被利用。为充分利用局部的差异信息,将直方图进行分区。每个分区图像的直方图作为一个特征向量,并将这些特征向量连接形成一个复合的特征向量。图像分区数量不同,得到的直方图向量差异不同,分区数量越多,向量维数越高,利用分区之间差异信息更为丰富,但计算消耗的时间更长。综合考虑计算速度与计算准确率,将直方图分成9个区。直方图相关性计算如下

(5)

(6)

式中N为直方图的维数,H1,H2为求解相关性的直方图。

2.3 主成分分析降维处理

直方图经分块处理后,维数急剧上升,且存在较多的冗余数据,直接用于匹配会使计算量大,计算过程复杂。利用主成分分析(principal component analysis,PCA)降维,能解决LBP直方图向量维数过高的问题[10]。

首先,设分块LBP直方图有向量集：X={X1,X2,X3,XN},Xi为第i个分块的直方图向量,N为分块数量。分块直方图的协方差矩阵表示为

(7)

式中E(X)为X的数学期望。

接着,对协方差矩阵求特征值λi,将λi从大到小排列,Ki为其对应的特征向量,Ki即为X的主分量矩阵,最后,重构原始数据。

Y=KT(X-E(X))

(8)

重构过程表示将数据X向某一个特征向量Ki进行投影,得到一组新的数据Y,选取前m个Ki便将数据X降到m维。经过变换得到的m维直方图保留了高维数据,利用了直方图分块之间的差异信息,有利于提高子区匹配的准确性。

2.4 亚像素位移计算

区域匹配的结果以像素为最小单位,实际的位移不是整像素值。计算其亚像素位移极大的提高了测量精度,研究人员采用的主要亚像素位移计算算法为：灰度插值法、曲面拟合法、灰度梯度法、梯度迭代法等。曲面拟合法具有精度高、计算效率高、抗干扰性强等优点,因此,本文选用该算法计算亚像素位移值。叠加子区匹配的整像素位移值与曲面拟合法计算出的亚像素位移值,得到最终测量位移值。

3 模拟散斑图仿真实验

用计算机模拟生成几组散斑图,可精准控制散斑图的位移、亮度信息,有效避免物体实际变形前后散斑图匹配过程中可能受到的其他干扰。变形前后的模拟散斑图灰度表示为

(9)

式中s为散斑颗粒的数目,r为散斑颗粒尺寸大小,(x0,y0)为散斑颗粒中心位置,I0为散斑颗粒中心位置的光强分布。u,v为散斑图两个方向上的位移。选取散斑颗粒平均半径为2,散斑颗粒数目为10 000。图5为基于matlab生成的模拟散斑图。

图5 基于MATLAB生成的模拟散斑

选定不同I0的值,模拟光照强度变化,设定不同位移值,模拟光照角度变化。选取散斑图中大小为41×41的子区为感兴趣区域。分别利用传统DIC方法与基于LBP的数字图像相关法对目标图像进行匹配。小位移时平均误差、标准差分别如图6(a)和图6(b)。大位移时平均误差、标准差分别如图6(c)和图6(d)。

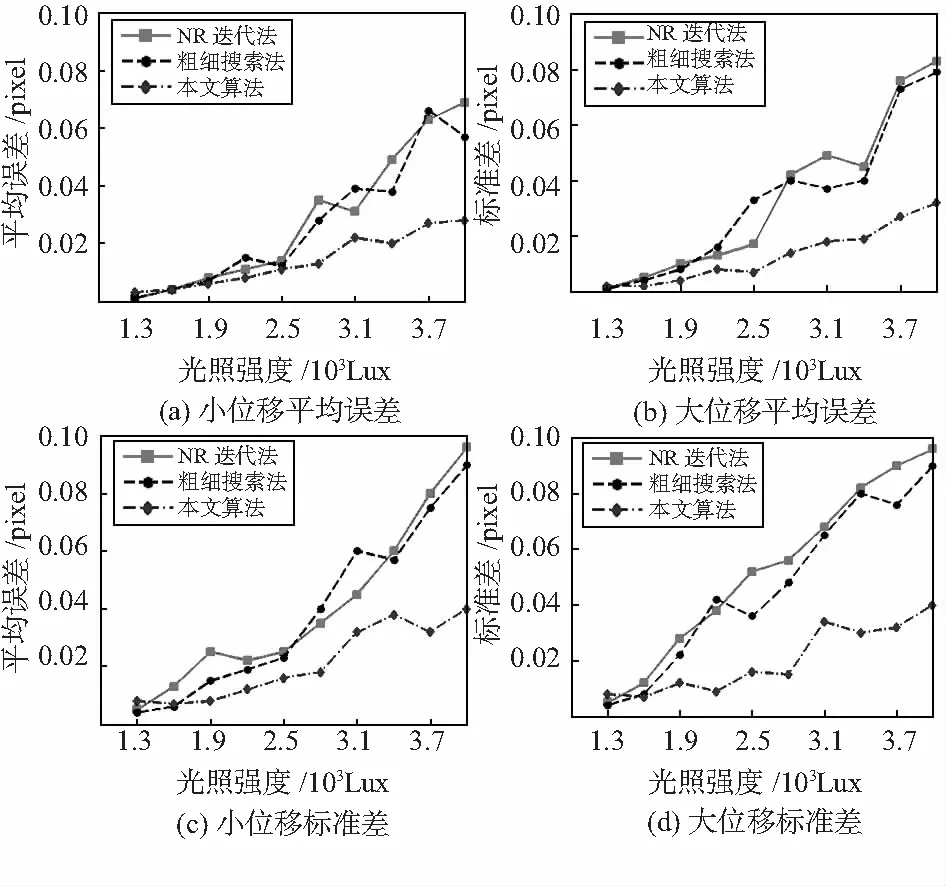
图6 仿真实验结果

模拟散斑实验结果表明,随着光强等级的增加与光照角度的变化,三种算法的误差平均值与标准差均呈递增趋势,但基于CS-LBP的数字图像相关法的误差增幅显著小于传统方法。

4 刚体平移实验

为了验证本文算法匹配结果的准确性,对刚体进行平移实验。选择尺寸合适的小铝板作为试件,在试件表面喷白色哑光漆作为背景色,黑色哑光漆模拟随机散斑点。将试件水平装夹在千分尺移动台上,平移精度为0.01 mm。采用Baumer的TXG12型号CCD相机,曝光时间设置8 μs,帧频为32 fps。辅助光源选用一组型号为LED—A4090的平面光圈,照度为80 000 Lux。具体实验装置如图7。

图7 实验装置

旋转移动台X方向旋钮,将试件分别平移0.76,1.26,2.37,3.91,4.31……9.46 mm距离,调整辅助光源亮度,对平移前后光照强度不同的图像分别采用N—R迭代法,粗细搜索法和基于LBP的数字图像相关法进行区域匹配。不同光照强度时测量均值误差见表1。

表1 不同光照时测量均值误差

基于CS-LBP的数字图像相关法在光照强度变化较小时,其绝对误差与传统的DIC方法基本相等。随光照强度的增加,该方法的误差增幅相较于传统方法减少了42.8 %。因此,在光照强度变化的实际应用中,利用该方法可以降低光照引起的误差,进而提高测量精度。

5 结 论

提出了一种基于CS-LBP的数字图像相关法,利用LBP算子的局部编码特性,有效降低了DIC在光照变化时的测量误差。模拟散斑图仿真分析与刚体平移实验结果充分说明了该方法的稳健性与准确性。