基于改进差分进化算法的云计算任务调度策略*

林 涛, 王 昊, 李 鹏

(河北工业大学 人工智能与数据科学学院,天津 300130)

0 引 言

云计算是一种基于分布式计算、并行计算和网格计算的新型的商业计算模式[1]。云计算采用服务的方式为用户提供动态虚拟化资源池[2],可以将用户提交的任务分配给分布式计算机资源池进行合理调度。由于资源是有限的,因此云计算系统服务是有偿的[3,4],在海量数据面前,云计算任务的调度成为影响云计算系统性能的关键因素,也决定了完成用户任务的成本,因此,如何充分利用云中资源对任务进行高效调度是云计算中的重点和难点。

近几年,一些人工智能算法已经被广泛的应用到任务调度问题中。文献[5]提出了一种完全多项式的在线算法,并采用整数规划方式减少应用程序延迟,优化云计算任务的卸载和调度策略,从而最大化节约资源。文献[6]将网络存储感知和贪心算法相结合,提出了一种贪心改进算法,大幅减少了数据在数据链路层所消耗的时间。文献[7]提出了一种多目标调度方案,即MOCS,实现了云计算环境下的低功耗和调度效率的优化。文献[8]针对资源虚拟化环境中的混合型负载调度问题,采用“最小能耗比例优先”的策略进行调度,在“调度偏差”和“相对能效”两方面优势明显。但这些方法在处理海量任务调度方面的效果均不够理想,且考虑影响因素过于单一。

本文通过分析云计算任务资源分配问题,综合考虑任务完成时间和执行能耗等因素,采用改进的差分进化算法制定合适的任务调度机制,以期快速而高效地为虚拟机资源尽可能地均衡分配任务。仿真实验的结果表明,本文提出的基于改进差分进化算法的云计算任务调度算法有效减少了云计算任务的完成时间,并大幅降低了任务的执行能耗。

1 云计算独立任务调度模型

云计算平台是在“需求付费”的原则下可同时为多个用户提供服务,且满足用户的多服务质量(quality of service,QoS)目标约束条件[9,10],但云计算在满足用户的同时,还应提高云服务提供商的收益。该调度模型着重考虑用户所关心的完成时间以及云服务提供商在意的能耗。

1.1 变量描述

任务调度是根据一定的约束规则将应用任务集与可用资源集建立的一种合理映射的关系。云环境下的任务分配目标是将M个任务合理的派发给云服务器上N个可利用的资源进行执行,尽可能减少任务的执行时间和执行能耗。R为资源节点rj的集合j∈[1,n],其中,n为云服务器可利用的资源数量；T为应用任务ti的集合,i∈[1,m],m为待调度计算任务的数量。通常,在任务调度过程中可用资源节点数量远远小于参与调度的任务数量,即r≪m。

将云计算任务调度问题用一个四元数组∑:(T,P,TIME,E)进行描述,其中，T为待调度的计算任务集合；P为m×n的任务分配矩阵,矩阵P中的元素pij=1表示计算任务ti在资源节点rj上执行,否则pij=0；时间执行矩阵TIME是一个m×n的矩阵,其元素timeij表示计算任务ti在资源节点rj上的执行时间；E为m×n的能量消耗矩阵,其元素eij表示任务ti在资源节点rj上执行消耗的能量。

1.2 任务建模

任务完成时间是指任务提交到任务完成,并将调度完成后的结果反馈给用户的时间间隔。由于计算任务是并行执行的,因此任务完成时间定义为所有计算任务中完成时间最长的任务所用时间

(1)

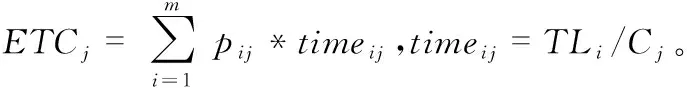
执行能耗是指任务执行完后,每个虚拟资源因执行任务而消耗的能量。每个调度方案中所有任务执行完成后所消耗的能耗定义为

(2)

式中eij为任务在云服务器上的执行能耗,eij=Ecpu·timeij。其中，Ecpu为云服务器CPU能耗,该执行能耗与CPU的利用率呈线性关系[11],Ecpu=αcpu·ucpu+γcpu。其中，ucpu为CPU利用率,αcpu和γcpu分别为CPU能耗公式中的固定系数。

以降低执行能耗与任务完成时间为目标,得到的云计算的任务调度目标函数可以称为最小化问题

minf(x)=λ1*AllTime(x)+λ2*EC(x)

(3)

式中λ1,λ2分别为任务完成时间、执行能耗的权重,且满足λ1+λ2=1,λ1>0,λ2>0。

2 改进的差分进化算法

本文提出了一种改进的差分进化算法,基于Levy分布的自适应差分进化(Levy-based adaptive differential evolution,LADE)算法,并将其应用于求解云计算任务调度问题。

2.1 染色体编码

本文结合云计算任务调度的特点,采用资源—任务的间接编码方式,用户的计算任务总数量为染色体长度,每个基因代表一个计算任务,该基因位的位值代表该计算任务分配到相应资源的资源编号。染色体最终编码格式如图1所示,ti表示任务编号,i∈[1,m],rj表示资源编号,j∈[1,n]。

图1 染色体编码格式

按照上图的编码方式可以得到对应的解码为r3:{t1},r1:{t2},r2:{t3},…,rn:{tm}，由此可以得出,每一条染色体对应一种任务的调度方案。

2.2 变异操作

本文采用随机选取种群中两个不同的个体与待变异个体进行向量合成,产生中间个体Vi(g+1),即

vi(g+1)=xi(g)+F[i]×(xp1(g)-xp2(g))

(4)

式中g为进化代数,xi(g)为第g代种群中第i个个体,xp1(g),xp2(g)分别为第g代种群中随机选取的两个不同个体。F[i]为每个个体特定的缩放因子,满足取值范围为[0,1]的柯西分布[12]

Fi=CauchyRandom(μF,0.1)

(5)

μF的更新方式

μF=(1-c)·μF+c·meanL(SF)

(6)

式中SF为所有成功变异的个体的F值的集合,meanL(•)为Lehmer均值[12]

meanL(SF)=∑FeSFF2∑FeSFF

(7)

2.3 交叉操作

对第g代个体{xi(g)}及其变异的中间体{vi(g+1)}进行交叉操作

(8)

式中jrand为[1,2,…,D]为的随机整数。每个个体i均有特定的交叉概率CR[i],满足Levy分布,其概率密度函数[13]

(9)

式中α,γ为Levy分布的2个特征参数；0<α≤2,γ>0。

2.4 贪婪选择

DE采用贪婪算法来选择进入下一代种群的个体,选取适应值更好的个体进入下一代,本文中,由于任务调度问题属于最小化问题,因此,选取适应值较小的个体进入下一代

(10)

2.5 DE任务调度算法的总流程

结合前文建立的多用户任务调度模型,得到改进之后的DE算法流程图如图3所示。

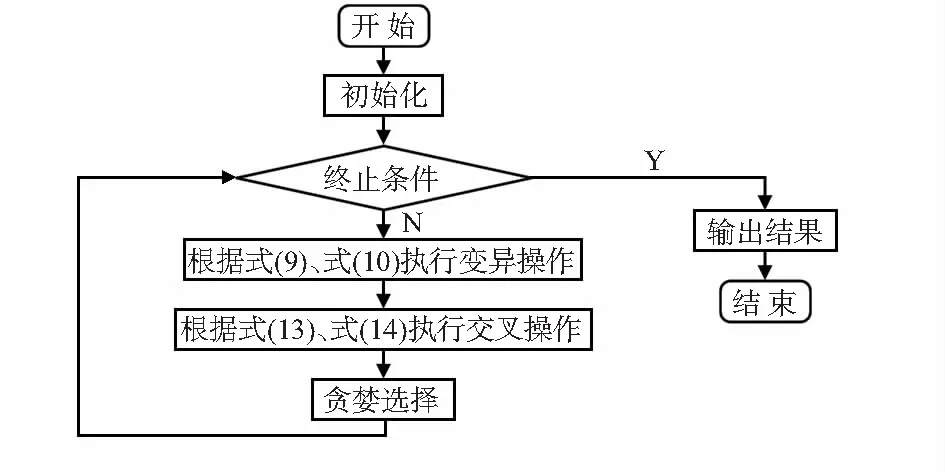
图3 算法流程

3 实验结果与分析

设计了2个实验方案：一是选取测试函数对比其他算法,验证本算法寻优的优越性；二是在Windows操作系统下,主频为2.5 GHz,采用Cloudsim-3.0.2[14]云计算模拟平台对本文算法的实际调度性能进行模拟仿真,并与传统DE[15]算法和jDE[16]算法进行比较。实验中通过改变任务参数来测试在不同计算任务数下算法的表现性能。

3.1 寻优测试

采用3个准测试函数：Sphere、Rosenbrock和Rastrigin对传统DE算法、jDE算法和LADE算法的性能进行了对比测试,所有算法的运行结果如图4所示。

图4 三种算法对三个准函数的寻优收敛曲线

对图4的分析可以看出,对3个准测试函数,LADE算法的性能均优于其他两个算法,对比结果表明,不管对于单峰函数还是多峰函数,LADE算法在迭代次数范围内表现出了良好的性能,目标函数值曲线下降速度快,寻优精度高,在一定程度弥补了算法易陷入局部最优的不足。

3.2 云计算调度测试

将设计的LADE算法在云计算模拟平台Cloudsim上进行模拟仿真。实验时所用的具体参数设置如表1。

为了尽量避免误差,本文将每组实验都进行10次,实验结果如图5。

表1 仿真实验各种类数据参数

图5 不同任务数量下三种调度策略任务仿真结果

由图5中可以看出,在计算资源不变的情况下,任务数量很小时,LADE和标准DE、jDE算法的差别不大,都能找到近似最优解。但随着任务数量的增多,调度复杂度也随之上升,LADE算法相比其他两个调度算法的优势愈加明显,说明LADE算法在任务数量多,复杂度高的环境下依然具有良好的调度性能。

表2显示了DE、jDE和LADE等3种算法分别在任务数为100,200,300,400,500时得到的适应值的均值、最大值、最小值、中值、标准差的对比结果。由表2可以看出,相较于其他两种算法,LADE得到的适应值对于所有的任务数都表现出了它的优势。当任务数为100时,LADE取得的适应值均值为1.74×103,其中最优的适应值为1.65×103,而其他两种算法最优的适应值为1.92×103；随着任务数的不断增加,当任务数为500时,LADE取得的适应值均值为9.38×103,其中,最优的适应值为9.21×103,而其他两种算法最优的适应值为1.06×104。可以看出,LADE在进化初期就有着很强的全局搜索能力,随着任务数越来越多,难度的提高,适应值相差也越来越多,LADE的优势也就越加明显。

另外,由表2还可以看出,随着任务数的不断增加,适应值也越来越大,这是因为任务数增加,相应的执行时间和执行能耗也会增加,对应的适应值也会随之增大。但是,对于不同的任务数量,LADE均表现出其明显优势。

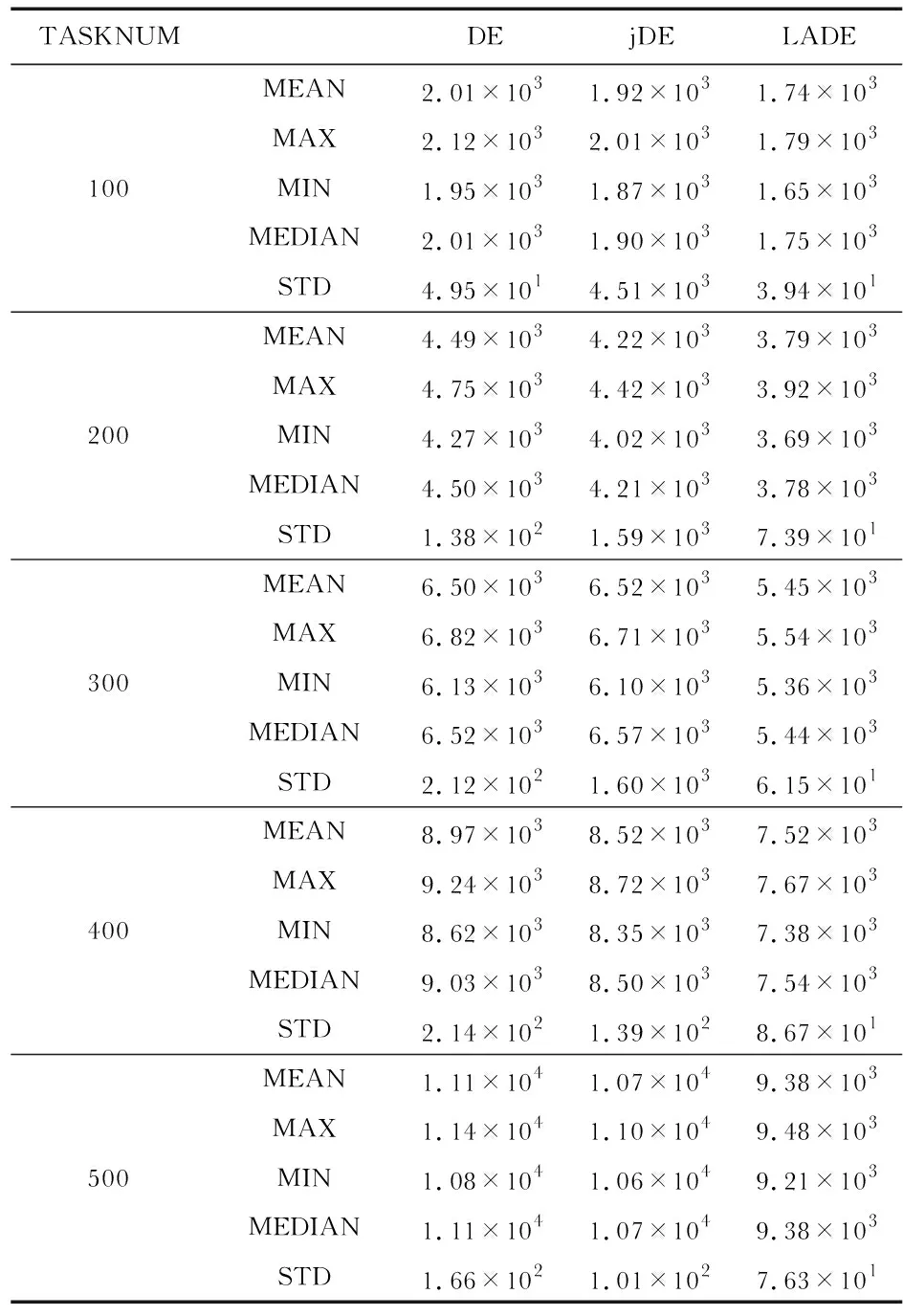
表2 三种算法适应值对比结果

4 结束语

实验结果证明：相对于传统DE算法和jDE算法,本文算法在计算资源有限,复杂度高的情况下的计算任务调度具有较明显的优势,能大幅减少任务的完成时间和执行能耗,在现代大规模云计算中有着广泛的应用前景。