翼型扑动气动特性数值模拟研究

李尚斌，罗 骏，江露生

(中国直升机设计研究所，直升机旋翼动力学重点实验室，江西 景德镇 333000)

0 引言

扑翼飞行器属于仿生范畴，自然界中鸟类和昆虫等飞行生物均采用扑翼飞行方式。

国内外已有研究者对扑翼飞行进行过研究。国外，Jones等[1]针对扑翼尾迹，展开了试验和计算相关研究；Smith等[2]采用面元法并结合有限元模型对柔性扑翼运动进行了研究；J.C.S.Lai等[3]针对不同的减缩频率和振荡位移展开试验研究，详细分析了振荡翼型的尾迹结构及产生推力的原因。Angela等[4]对鸽子起飞和着陆动力学进行了研究。国内，宋笔锋等[5-7]开展了翼型厚度、翼型开孔对扑翼的气动特性的影响以及微型扑翼的推进特性试验等研究；昂海松等[8-9]开展了适合于扑翼的动态网格生成方法及仿生扑翼机构设计等研究。

本文将扑动简化为俯仰、沉浮和平移三种运动，通过求解NS方程，数值模拟了二维翼型扑动非定常流动，分析了减缩频率、平均俯仰角、俯仰振幅和沉浮振幅对翼型扑动气动特性的影响规律以及流场涡分布特性。

1 计算模型

选NACA0012翼型为计算模型，将扑动简化为俯仰、沉浮和前飞三种运动，运动规律用以下函数表示：

α=α0+α1×sin(2×π×t/T);

h=H×sin(2×π×t/T+φ);

v=V;

式中，t(s)为时间，T(s)为扑动周期；α0(°)为平均俯仰角，α1(°)为俯仰振幅，α(°)为t时间俯仰角；H(m)为沉浮振幅，h(m)为t时间沉浮距离；φ(rad)为相位角；v(m/s)为前飞速度；k为减缩频率，ω(rad/s)为扑动角速度,C(m)为翼型弦长。

2 数值模拟

2.1 计算方法

网格为结构O型网格，第一层网格距物面的距离为1×10-5倍弦长。

以NS方程作为流动控制方程，并采用有限体积法对方程进行空间离散,差分格式为二阶迎风格式，湍流模型采用SST模型。NS方程如下:

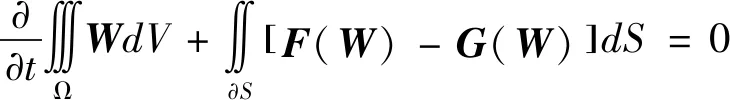
(1)

其中W是守恒变量，F(W)是无粘通量，G(W)为粘性通量，具体表达如下：

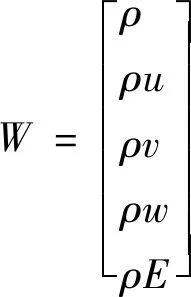
(2)

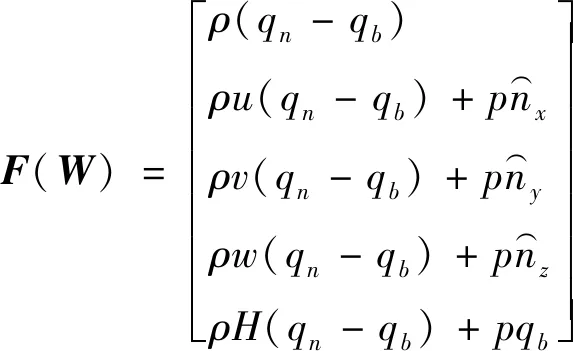
(3)

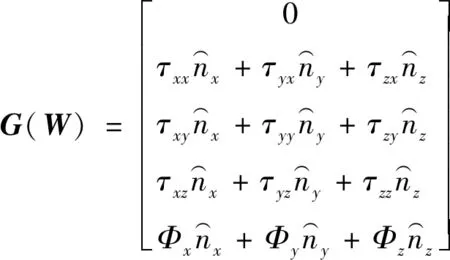
(4)

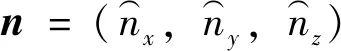
2.2 算例验证

这里选取Lee等人[10]典型的低雷诺数试验状态来验证该文的数值方法。缩减频率k=0.1，雷诺数Re=1.35×105，来流马赫数Ma∞=0.0385，平均攻角α0=10°，俯仰幅度α1=15°，无沉浮运动。

图1-图3分别为升力系数、阻力系数和力矩系数随攻角在一个周期内的变化图。从图中可以看出，计算值和试验值变化趋势一致，误差在合理范围内，计算结果可信。

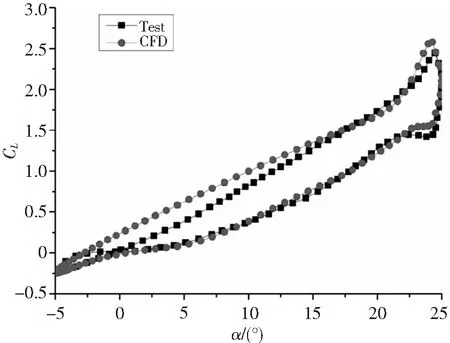
图1 升力系数随攻角变化图

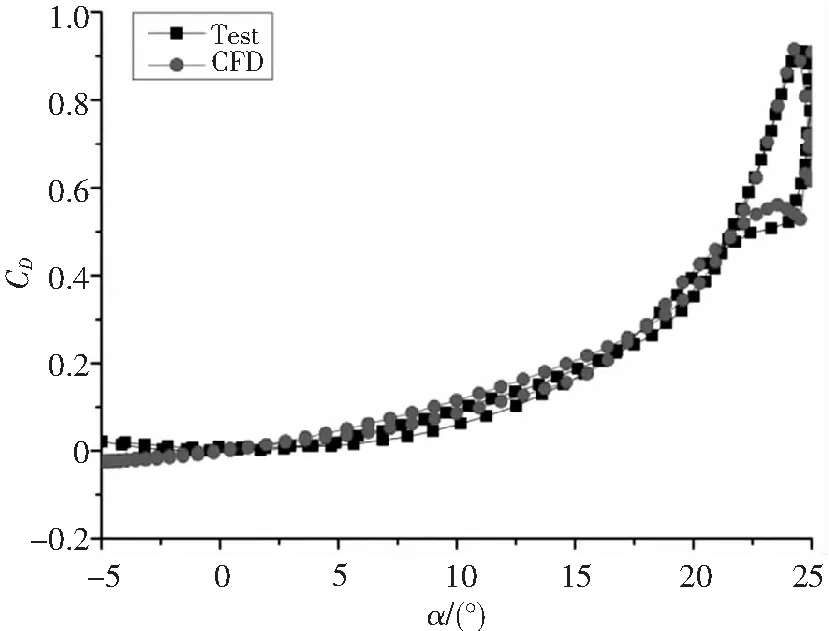
图2 阻力系数随攻角变化图

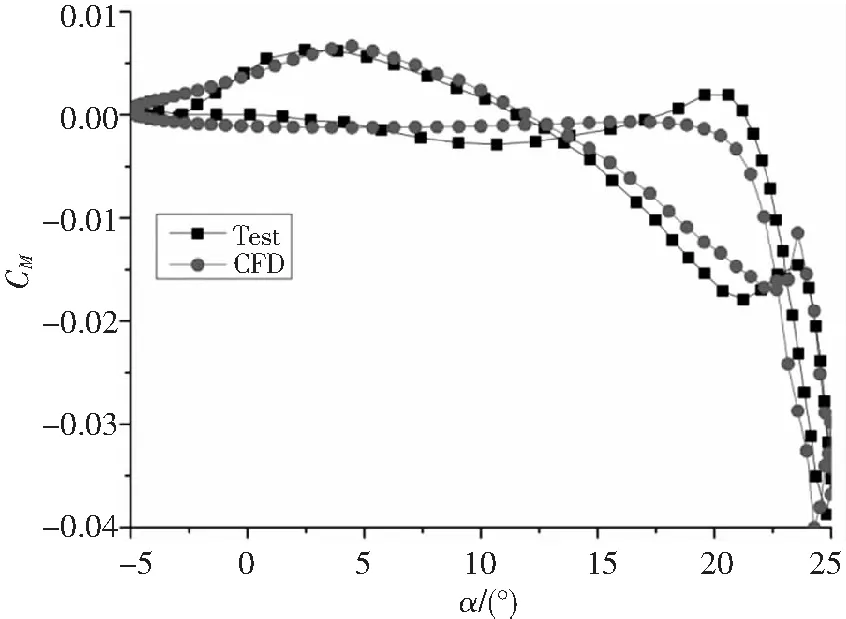
图3 力矩系数随攻角变化图

3 结果分析

结果分析中出现的公式如下：

(5)

式中，L为升力，垂直来流方向，向上为正，D为阻力，平行来流方向，负数表示向前推，M为力矩，力矩点在0.25弦线处；ρ为空气密度，v为来流风速，S为面积，C为弦长；CL为升力系数，CD为阻力系数，CM为力矩系数。

结果分析中，俯仰和沉浮运动相位差为π/2，0～0.5t/T内为上扑阶段，0.5～1.0t/T内为下扑阶段，0t/T时刻处在最低位置，0.5t/T时刻处在最高位置，0.25t/T时刻俯仰角最大，0.75t/T时刻俯仰角最小。

3.1 减缩频率影响分析

图4-图6为α0=10°，α1=15°，H/C=1状态下不同减缩频率的升力系数、阻力系数和力矩系数随时间变化图。k=0.2、0.25、0.30、0.35分别对应Re=82726、66207、55150、47253。

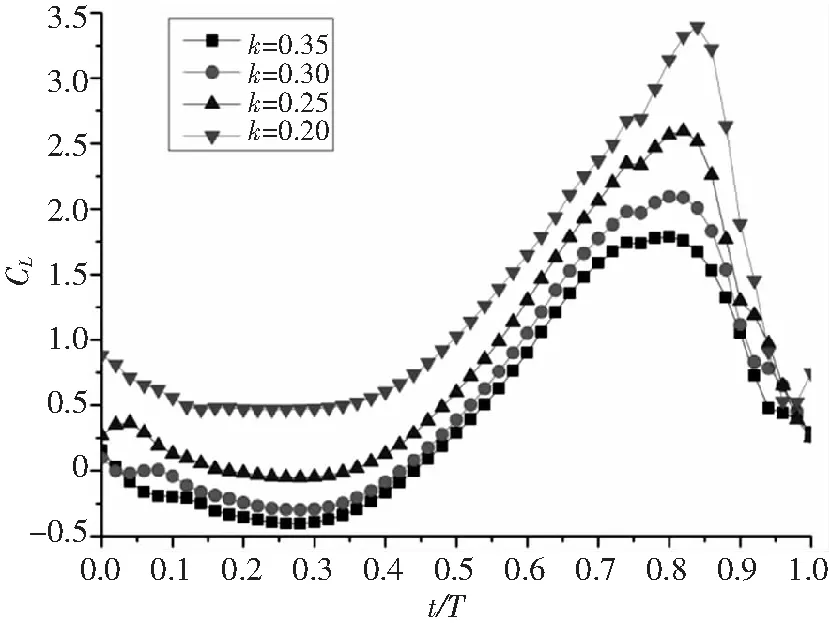
图4 不同减缩频率升力系数随时间变化图

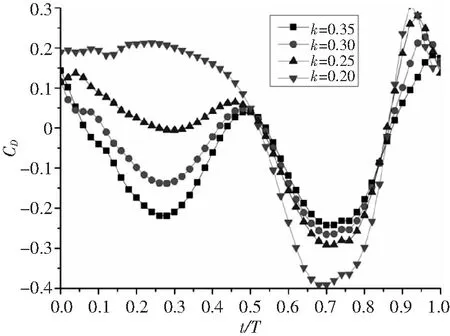
图5 不同减缩频率阻力系数随时间变化图

从图中可以看出，对于CL，k越小，平均升力越大；下扑时CL比上扑的大；k值大时，上扑产生向下的升力，下扑产生向上的升力，k值小时，上扑和下扑均产生向上的升力。对于CD，k越大，向前的平均推力越大；k值大时，上扑和下扑均产生向前的推力，k值小时，上扑产生向后的阻力，下扑产生向前的推力。对于CM，0～0.25t/T和0.75～1.0t/T，k越小，CM越大;0.25～0.5t/T，k越大，CM越大;0.5～0.75t/T，不同k值CM差别不大。

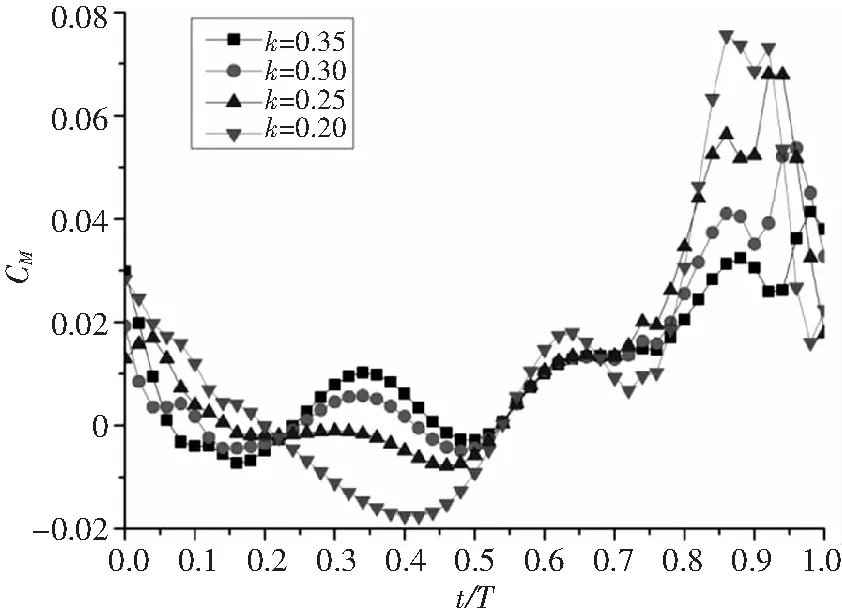
图6 不同减缩频率力矩系数随时间变化图

3.2 平均俯仰角影响分析

图7-图9分别为Re=66207，α1=15°，H/C=1，k=0.25状态下不同平均俯仰角的升力系数、阻力系数和力矩系数随时间变化图。

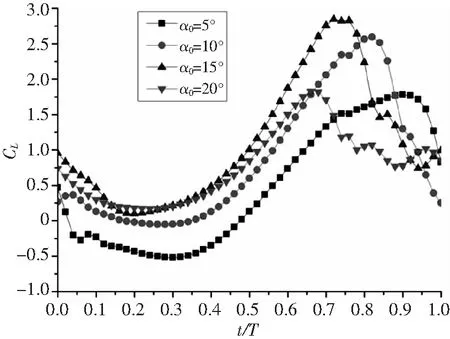
图7 不同平均俯仰角升力系数随时间变化图

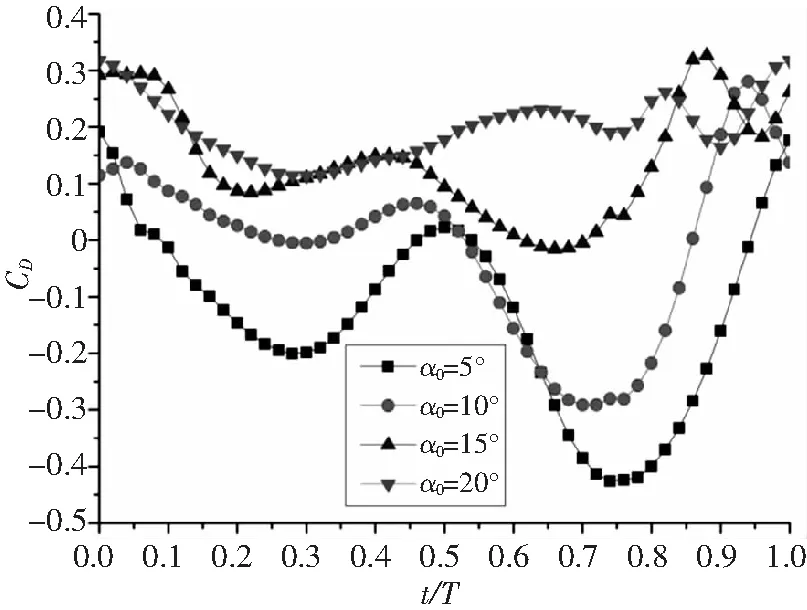
图8 不同平均俯仰角阻力系数随时间变化图

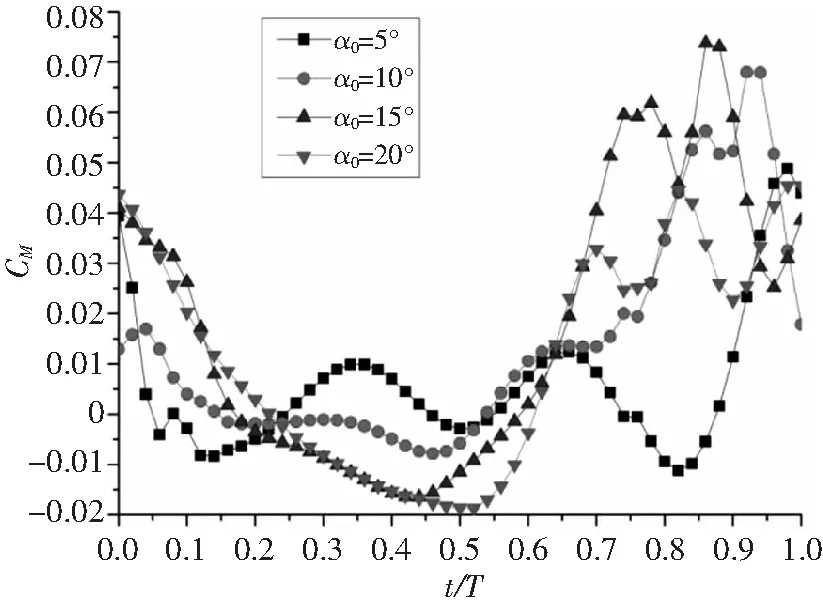
图9 不同平均俯仰角力矩系数随时间变化图

从图中可以看出，对于CL，下扑时CL比上扑的大；α0值大时，上扑和下扑均产生向上的升力，α0值小时，上扑产生向下的升力，下扑产生向上的升力；当α0≤α1时，α0越大，平均CL越大，α0=20°大于α1时，CL反而开始减小。对于CD，α0越小，向前的平均推力越大，但CD的相对波动越大；α0值小时，上扑和下扑均产生向前的推力，α0值大时，上扑产生向后的阻力，下扑产生向前的推力。对于CM，0～0.25t/T，α0越大，CM越大，0.25～0.65t/T，α0越小，CM越大，0.65t/T后规律不明显。

3.3 俯仰振幅影响分析

图10-图12分别为Re=66207，α0=10°，k=0.25，H/C=1状态下不同平均俯仰振幅的升力系数、阻力系数和力矩系数随时间变化图。

从图中可以看出，对于CL，下扑时CL比上扑的大；α1值小时，上扑产生向前的推力，下扑产生向后的阻力；α1值大时，上扑产生向后的阻力，下扑产生向前的推力；当α1=α0时，上扑和下扑均能产生向前的推力，但下扑后阶段产生向后的阻力。对于CM，类似k对CM的影响规律。

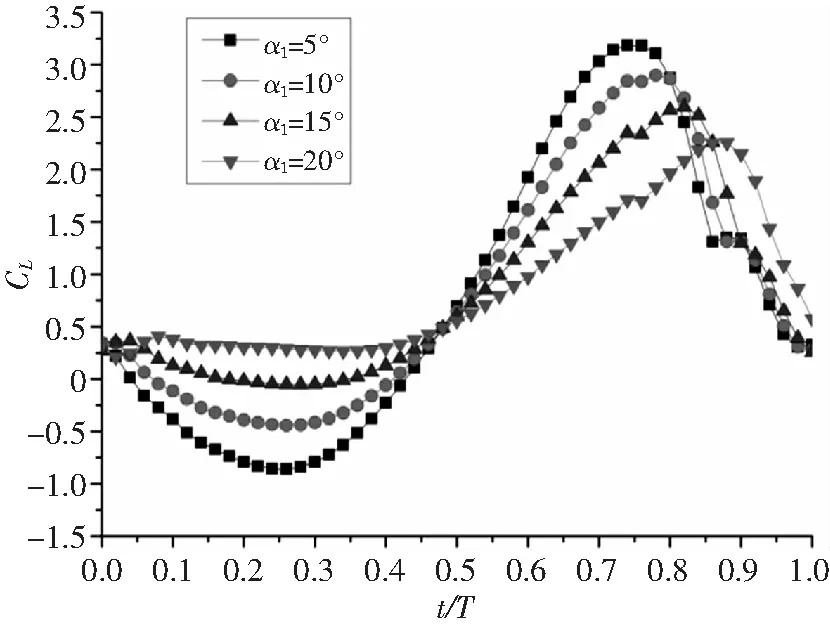
图10 不同俯仰振幅升力系数随时间变化图

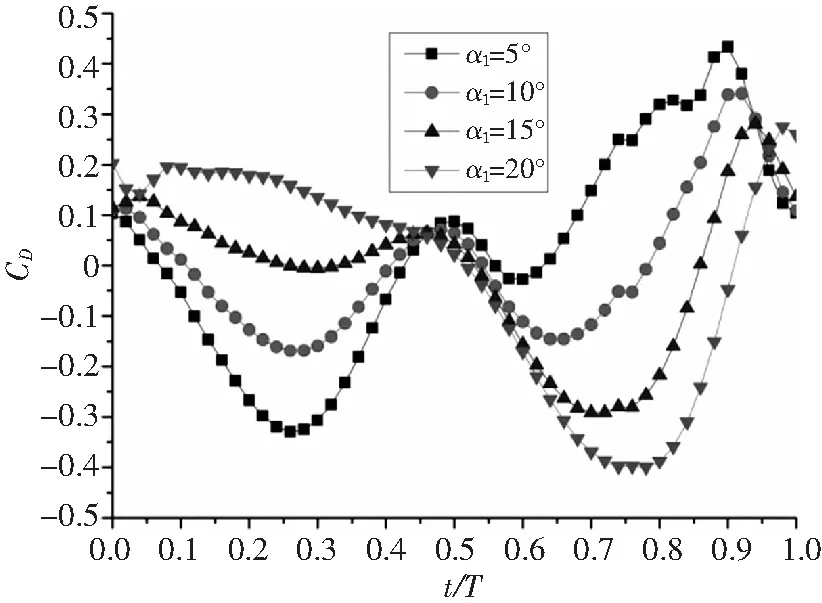
图11 不同俯仰振幅阻力系数随时间变化图

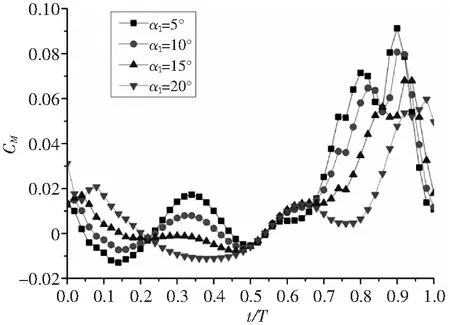
图12 不同俯仰振幅力矩系数随时间变化图

3.4 沉浮振幅影响分析

图13-图15分别为Re=66207，α0=10°，α1=15°，k=0.25状态下不同沉浮振幅的升力系数、阻力系数和力矩系数随时间变化图。

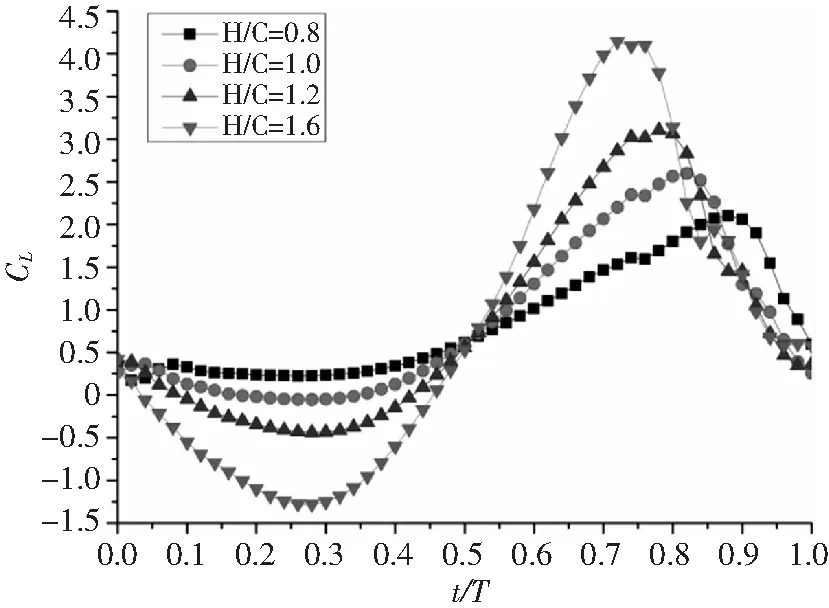
图13 不同沉浮振幅升力系数随时间变化图

从图中可以看出，对于CL，H越小，平均升力越大；下扑时CL比上扑的大；H值小时，上扑和下扑均产生向上的升力，H值大时，上扑产生向下的升力，下扑产生向上的升力。对于CD，H越大，向前的平均推力越大；H值大时，上扑和下扑均能产生向前的推力，但下扑后时间段也产生向后的阻力，H值小时，上扑产生向后的阻力，下扑前时间段产生向前的推力，下扑后时间段产生向后的阻力。对于CM，H大时，周期范围内CM值波动范围大；H小时，上扑CM值变化相对平缓，下扑变化更大。

图14 不同沉浮振幅阻力系数随时间变化图

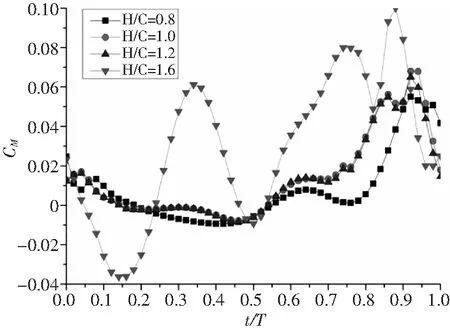
图15 不同沉浮振幅力矩系数随时间变化图

3.5 流场涡分布

图16为Re=66207，α0=10°，α1=15°，H/C=1，k=0.25状态下不同时刻涡线分布图。t/T=0位于最低点，t/T=0.5位于最高点。从图中可以看出，最低点时翼型前缘和后缘出现明显的涡，上扑过程中，前缘和后缘脱出的涡逐渐耗散，但前缘拖出的涡耗散得更快；下扑过程中，前缘拖出新的涡，并逐渐向后移动，涡强也随之增强。对比(a)和(h)图可以看出，(a)图中后缘涡是由前缘脱出的并移动到后缘，(h)图中前缘脱出的涡强度明显比后缘脱出的大。

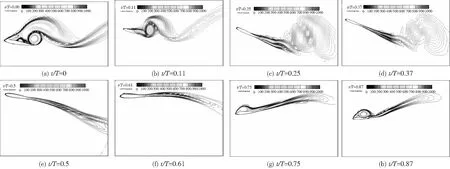
图16 不同时刻涡线变化图

4 结论

通过数值模拟分析，得出了以下结论：

1)研究范围内，增大平均俯仰角、俯仰振幅或减小减缩频率和沉浮振幅能有效提高升力；

2)研究范围内，减小平均俯仰角或增大缩减频率、俯仰振幅、沉浮振幅能有效增大向前推力；

3)研究范围内，升力主要由下扑阶段产生，α1≥α0时，可获得升力及推力的综合效果；

4)下扑过程中，前缘脱出涡并向后移动，强度逐渐变强，上扑过程中，涡逐渐耗散并继续向后移动。