单片机技术在物理排水实验中的应用研究
王颖 王清辉 杜开初
【摘 要】 本文基于单片机的物理排水实验测量装置是基于单片机技术、传感器技术和计算机技术,实现了物理排水实验中的液位高度变化与时间关系的自动测量,解决了传统人工秒表读取数据带来的误差大和实验时间长的问题。使用该装置可以提高实验效率,并为后续的分析建模提供更精准的数据。
【关键词】 分布特性;数学模型;一元线性回归分析;求解积分方程
【中图分类号】 TM93 【文献标识码】 A
【文章编号】 2096-4102(2019)03-0100-03 开放科学(资源服务)标识码(OSID):
物理学是一门以观察、实验为基础的科学,物理实验对于学生掌握物理基本知识有着不可替代的作用。物理学的原理、定理是在总结大量的物理实验事实基础上概括出来的。我们试图用水柱高度h及其相应排干水的时间t的几组实验及其数据的处理,得到t~h关系式。传统实验是分别在同一容器中装入不同高度的水,分别测出水流光所用的时间,实验繁琐且误差大;本次设计了基于单片机测量的系统装置,具体如下。
1实验装置及原理
1.1系统介绍
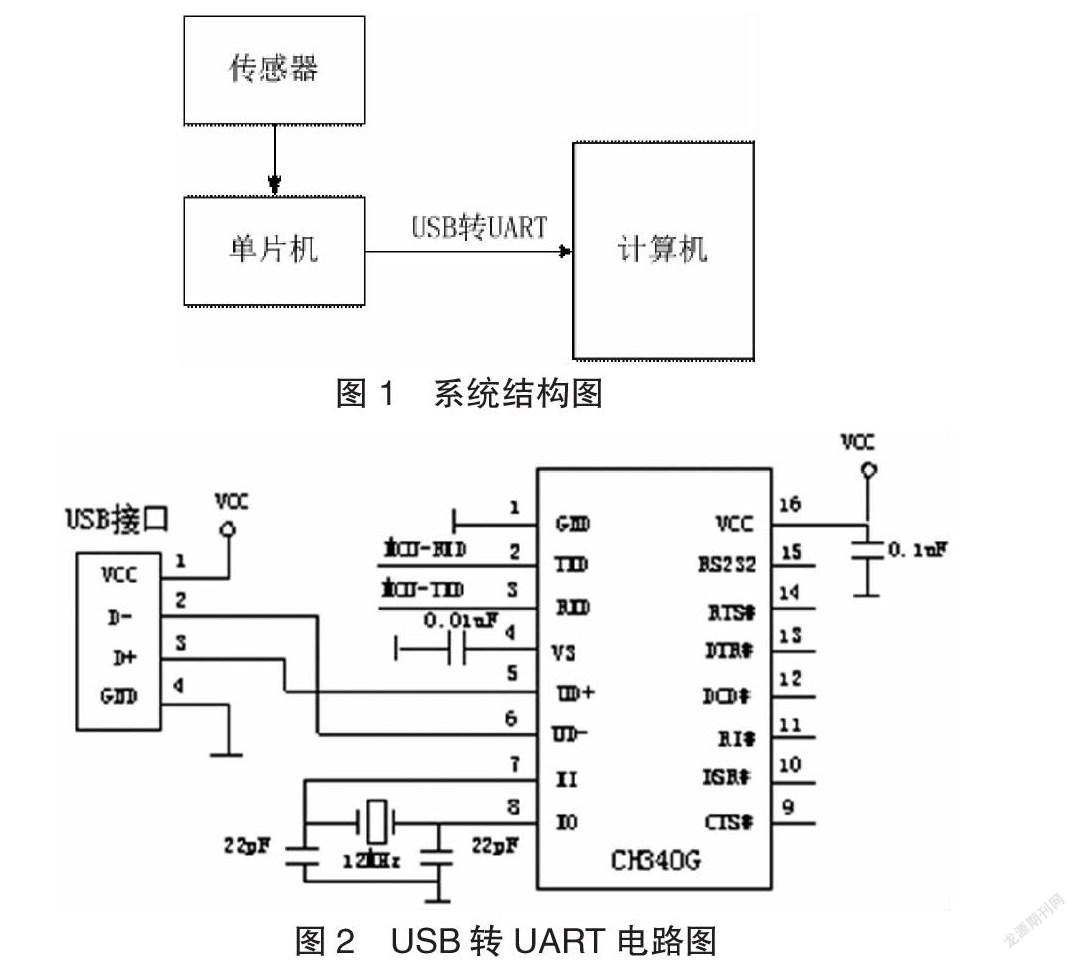
单片机选用STC15W4K32S4系列单片机。该单片机具有10位的AD转换、32KBROM、4KBRAM、5路16位定时/计数器等硬件资源。系统结构图如下图1所示。图中传感器由安装在水筒上的检测线组成,通过I/O口连接到单片机的AD口;单片机通过AD口检测各次水位的下降时间点,再根据定时器的定时值来记录水位下降过程中各次对应的消耗时间;计算机和单片机通过USB转UART完成通讯,收集单片机检测的各次水位对应时间值进行记录。
其中USB转UART电路和计算机上位机软件如下介绍:
(1)USB转UART电路
大部分的笔记本电脑都没有自带UART串口,而是USB接口。为了实现单片机和计算机之间的有线数据传输,可以使用USB转UART模块来完成。目前用的比较多的转换接口芯片是CH340G,具体电路图如下图2所示。图中MCU-RXD和MCU-TXD引脚分别接单片机的串口引脚RXD和TXD,因此CH340G的RXD和TXD与单片机的TXD和RXD连接,实现收发的正常进行。
(2)计算机上位机软件
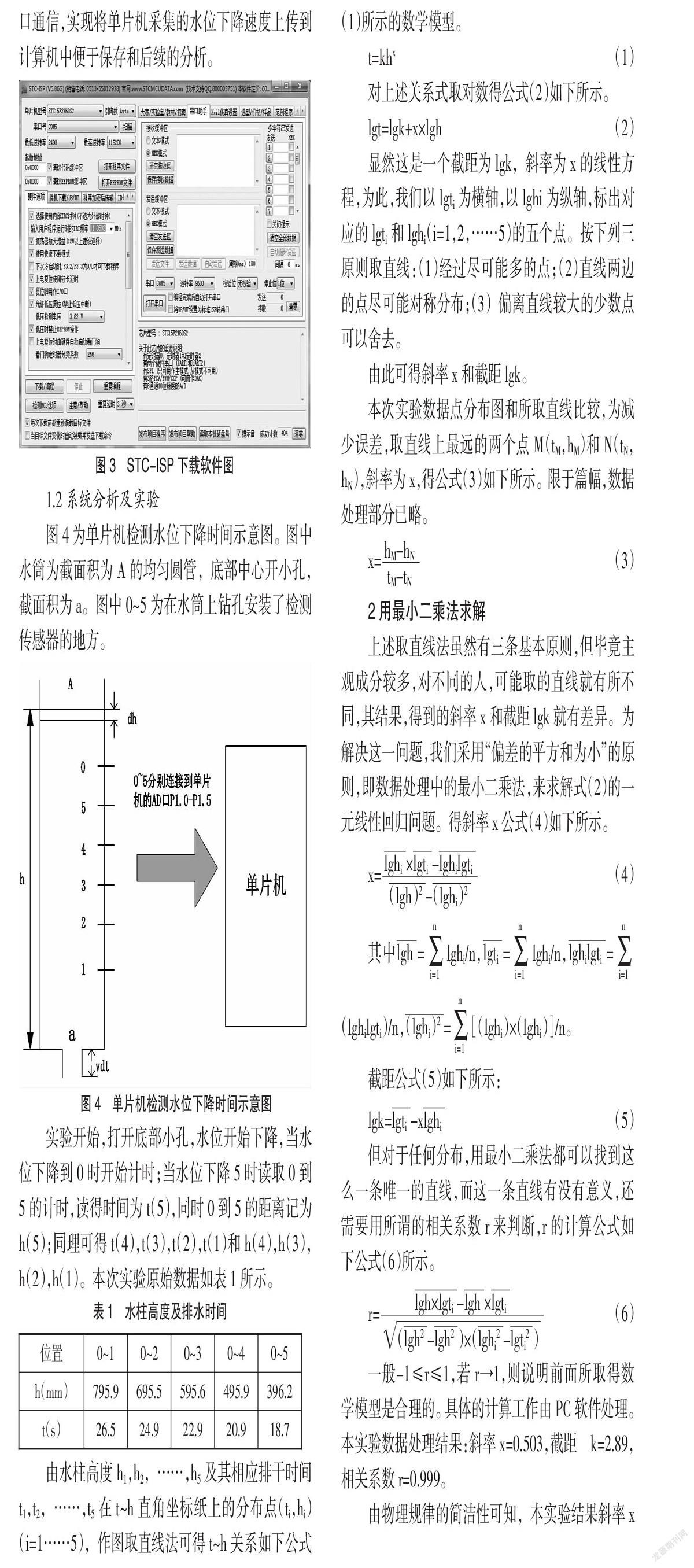
计算机接收数据的软件可以采用STC公司提供的STC-ISP下载软件,自带的串口调试助手来完成数据的接收和保存。软件界面如下图3所示。图中设置好串口和波特率就可以完成和单片机的串口通信,实现将单片机采集的水位下降速度上传到计算机中便于保存和后续的分析。
1.2系统分析及实验
图4为单片机检测水位下降时间示意图。图中水筒为截面积为A的均匀圆管,底部中心开小孔,截面积为a。图中0~5为在水筒上钻孔安装了检测传感器的地方。
实验开始,打开底部小孔,水位开始下降,当水位下降到0时开始计时;当水位下降5时读取0到5的计时,读得时间为t(5),同时0到5的距离记为h(5);同理可得t(4),t(3),t(2),t(1)和h(4),h(3), h(2),h(1)。本次实验原始数据如表1所示。
由水柱高度h1,h2,……,h5及其相应排干时间t1,t2,……,t5在t~h直角坐标纸上的分布点(ti,hi)(i=1……5),作图取直线法可得t~h关系如下公式(1)所示的数学模型。
对上述关系式取对数得公式(2)如下所示。
显然这是一个截距为lgk,斜率为x的线性方程,为此,我们以lgti为横轴,以lghi为纵轴,标出对应的lgti和lghi(i=1,2,……5)的五个点。按下列三原则取直线:(1)经过尽可能多的点;(2)直线两边的点尽可能对称分布;(3)偏离直线较大的少数点可以舍去。
由此可得斜率x和截距lgk。
本次实验数据点分布图和所取直线比较,为减少误差,取直线上最远的两个点M(tM,hM)和N(tN,hN),斜率为x,得公式(3)如下所示。限于篇幅,数据处理部分已略。
2用最小二乘法求解
上述取直线法虽然有三条基本原则,但毕竟主观成分较多,对不同的人,可能取的直线就有所不同,其结果,得到的斜率x和截距lgk就有差异。为解决这一问题,我们采用“偏差的平方和为小”的原则,即数据处理中的最小二乘法,来求解式(2)的一元线性回归问题。得斜率x公式(4)如下所示。
但对于任何分布,用最小二乘法都可以找到这么一条唯一的直线,而这一条直线有没有意义,还需要用所谓的相关系数r来判断,r的计算公式如下公式(6)所示。
一般-1≤r≤1,若r→1,则说明前面所取得数学模型是合理的。具体的计算工作由PC软件处理。本实验数据处理结果:斜率x=0.503,截距 k=2.89,相关系数r=0.999。
由物理规律的简洁性可知,本实验结果斜率x应该为0.5,即数学模型应该为t=k 才是合理的。由此得本实验相对误差为0.6%。而相关系数r=0.999,显然是密切相关,这说明我们根据数据分布特性而选取的数学模型t=khx是合适的。由此可得到结论:我们用水柱高度hi及其相应排干水的时间ti的五组实验及其数据的处理,得到了t=k 关系式,实现了予期的目标。
综上所述,本实验设备简单价廉,只要透明水管、直尺和秒表,实验方法简便快捷,测五组实验数据,便可得t=k 关系式。同理,可应用于RC放电曲线的研究。
3理论分析
如图1所示,水位高度为h处,水位下降dh,其体积为-Adh。
此时由小孔排出的流体体积为a·Vdt。按不可压缩的理论流体的性质得公式(7)如下所示。
水位下降dh这一部分液体中质量为m的液体的势能为mgh,而对应排出流体的质量为m的动能为■mV2,按能量守恒定律如下公式(8)所示。
由(8)得公式(9)如下式所示:
将公式(9)带入代入公式(7)得:
两边取定积分得公式(11)如下所示:
解公式得t得计算公式如下公式(12)所示:
显然,实验结果和理论分析是一致的。可见本实验设计方案是可行的,而且和传统实验相比较具有操作简单、数据采集方便,误差小的特点。
4结论
文中提出基于单片机的物理排水实验测量装置。该装置基于单片机技术、传感器技术和计算机技术,实现了物理排水實验中的液位高度变化与时间关系的自动测量,解决了传统人工秒表读取数据带来的误差大和实验时间长的问题,根据检测的实验数据可以建立相应的数学模型进行后续的分析。使用该装置可以提高实验效率,并为后续的分析建模提供更精准的数据。
【参考文献】
[1]翁雪玲.物理实验教学对物理学科学习的作用[J].课程教育研究,2016(17):282-283.
[2]丁向荣,陈崇辉.单片微机原理与接口技术[M].北京:电子工业出版社,2015:16-32.
[3]丁向荣.嵌入式C语言程序设计[M].北京:电子工业出版社,2016:27-31.
[4]徐炜君,原大明.视日轨迹太阳能反馈跟踪系统的设计与实现[J].化工自动化及仪表,2016,43(8):855-858.
[5]赖义汉,王清辉,温发林,等.单片机原理及应用[M].成都:西南交通大学出版社,2016:43-46.
[6]何云宝.充分认识物理理论与物理实验的关系[J].内蒙古科技与经济,2001(4):133.
[7]林抒,龚镇雄,主编.普通物理实验[M].北京:人民教育出版社,1981:37-42.

