哑铃型钢管混凝土系杆拱桥吊杆索力测试研究

赵青 卢康 程龙树

摘要：本文以某哑铃型钢管混凝土系杆拱桥为研究对象，详细介绍了索力的计算方法和试验方法.利用桥梁的Midas计算软件，建立有限元模型，进行理论分析，现场进行加载荷试验，得到测量数据.通过现场的实测数据与理论数据的综合分析，进一步验证索力与其自身频率关系的科学性与准确性，从而对桥梁吊杆结构做出评价.

关键词：系杆拱桥;吊杆;索力测试;弦振动理论

中图分类号：TU312  文献标识码：A  文章編号：1673-260X（2019）04-0121-04

0 引言

随着经济的快速发展，桥梁作为路桥交通系统的重要组成部分，对桥梁的检测要求也越来越高.在系杆拱桥中，各类荷载都会通过吊杆进行传递.而索力作为直接承担桥梁荷载的重要研究对象，同时也控制着整个桥梁上部结构的内力分布情况与线型构造情况.2012年，攀枝花市的金沙江大桥一根吊杆的脱落，导致大桥发生部分塌陷，对以后的使用造成了严重的安全隐患.截至到目前为止，由于吊杆破坏而带来的工程损坏还在不断的发生，这就要求专业人员加强对吊杆的检测与监控，实时了解吊杆的变化，为降低桥梁事故的概率提供可靠的依据.

本次试验测试通过Midas计算软件，模拟分析拱桥在车辆荷载加载作用下吊杆的受力荷载的影响线，从而确定出荷载的加载位置，并将此加载方法与振动频率法应用于某哑铃型钢管混凝土系杆拱桥.将模拟的理论数据与现场的实测数据进行对比分析，发现振动频率法具有较高的准确性与科学性，基本符合规范要求，同时也为同类桥梁结构的吊杆索力分析评估提供重要依据与参考.

1 工程概况

该桥为哑铃型钢管混凝土系杆拱桥，桥面宽度为20.9米，双向四车道公路.车行道宽2×7.5m，人行道宽2×1.5m.上部结构是一个钢管混凝土拱，跨度为84米，计算跨度为78.5米，跨度比为1/4.拱肋由16Mn，12mm厚的钢板轧制成.其理论拱轴线为二次抛物线.在哑铃拱肋之间使用两对风撑，并且肋通过吊杆与系杆连接.共有两侧18对吊杆，吊杆采用PE索，颜色为乳白色，相邻吊杆的间距为4m.

2 索力测试理论及方法

振动频率法是一种测试结构固有振动频率并分析其固有振动特性以确定拉索索力值的方法.将测试仪器的振动检测器安装在测试部位上，拾取振动信号，进行过滤，放大和频谱分析，最后获得吊杆的固有频率.根据索力值与吊杆频率之间的固有关系确定索力值的大小.同时索力测试仪对信号采集后快速自动进行傅里叶变换并显示频谱图，若存在等间距的各阶频率，相邻波段的间距值大小就是所需要的基频f1.在现场实际测量时，吊杆自振的频谱是否准确可以通过这一特性来判断.

振动频率法使用方便，快速，灵活，成本较低，其设备可以重复利用，在斜拉桥梁拉索、吊杆张拉力，预应力钢筋、钢铰线张拉和受拉索道张拉力测试以及桥梁后期的检测和日常养护应用广泛.此方法对于数据采集时的抗干扰能力差，但只要准确的操作，同样也可以达到很高的精度.

2.1 基本假设

为了工程计算的需要，假定单位质量为W的拉索在张力T的作用下被张紧，吊杆拉索的刚度为EI.同时吊杆的垂度和弯曲在此次测试时数值都不大，即吊杆的轴线为直线;吊杆的两端同时也是固定不动的;在振动时吊杆的微元段重量相对其两端的张力忽略不计.

2.2 张力弦振动理论

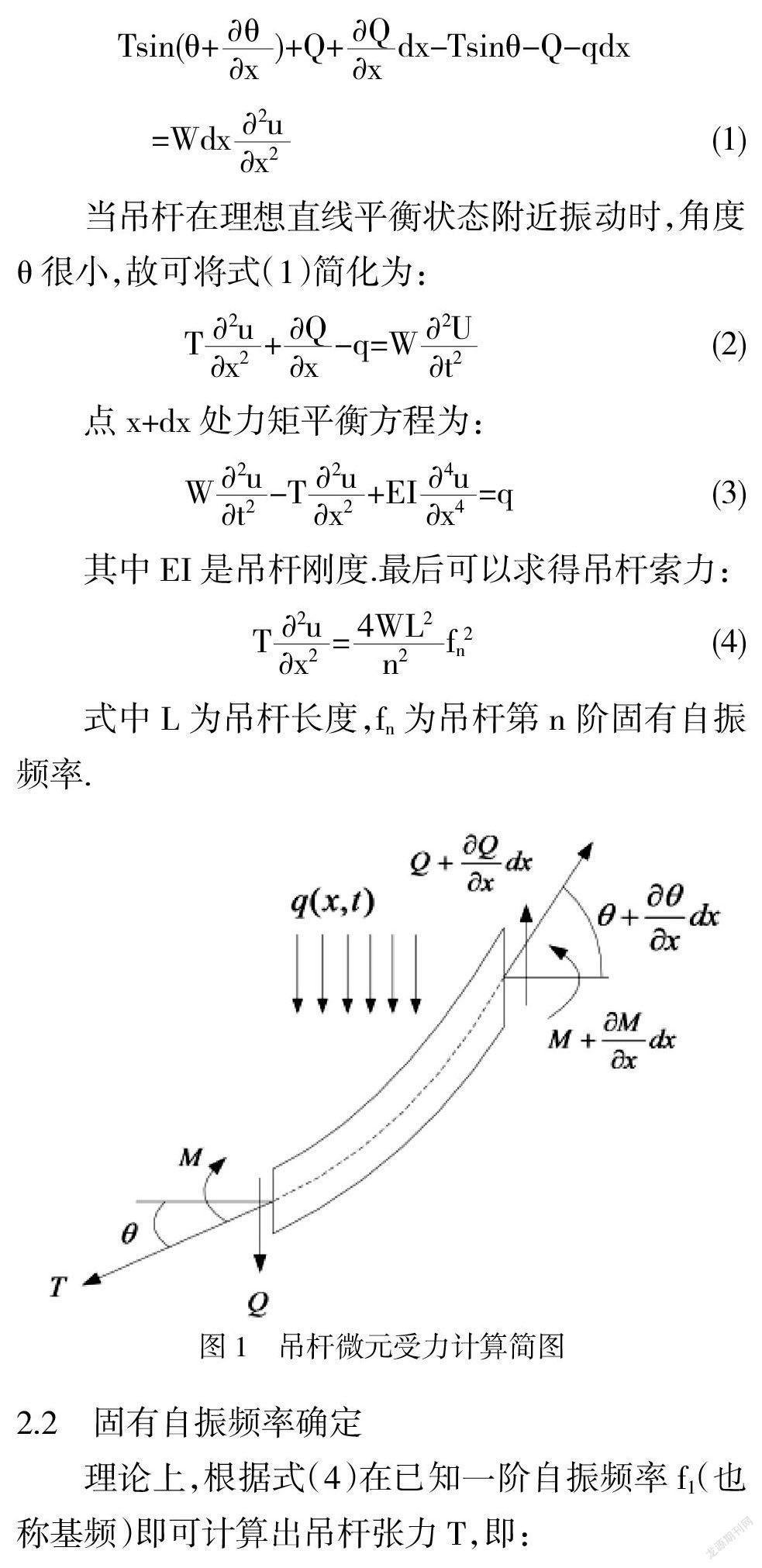
假定吊杆在任意点沿x轴的垂直方向发生振动，取微元弧进行分析，当吊杆沿速度方向作微幅振动时，在吊杆的微段上作用有张力、惯性力、弯矩和剪力以及干扰力（计入吊杆重力在内）.吊杆微元 的受力情况如图1所示.考虑弯曲引起的变形，不计剪切引起的变形以及转动惯量的影响，则在t时刻运动方程为：

2.2 固有自振频率确定

理论上，根据式（4）在已知一阶自振频率f1（也称基频）即可计算出吊杆张力T，即：

式（6）和（7）可以表达为高阶自振频率为其基频的整数倍.

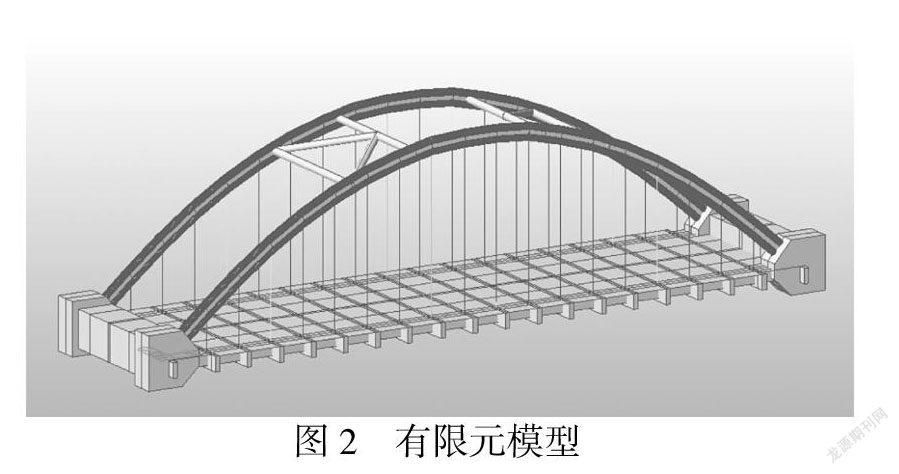
3 有限元模型的建立

采用Midas Civil 2015对本桥梁建立空间有限元模型，如图2所示，全桥吊杆为离散独立的桁架单元，桥面为板单元，其余为梁单元.整个桥梁分为222个节点和423个单元，其中36个是桁架单元，250个是梁单元，137个是板单元.吊杆的单位质量为14.052kg/m，在模型中各构件所采用的材料与几何特性参数均与实际一致.通过对本桥的有限元模型进行理论分析，得出对桥梁稳定性影响最大的位置，作为试验荷载加载的最不利工况的依据，获取理论计算数据.

4 试验加载工况

通过利用Midas Civil 2015计算软件对本桥三维空间有限元模型的分析，得到了对桥梁稳定性影响最大的截面位置.根据桥梁规范的规定，并经过结构分析计算确定该桥的内力控制截面，建议在1/2跨度上进行加载.采用6辆运输装载车（每个重约310kN）进行对称满载和偏载满载加载，并在最不利的部署形式下测试所选吊杆的索力值的变化.

5 测点布置

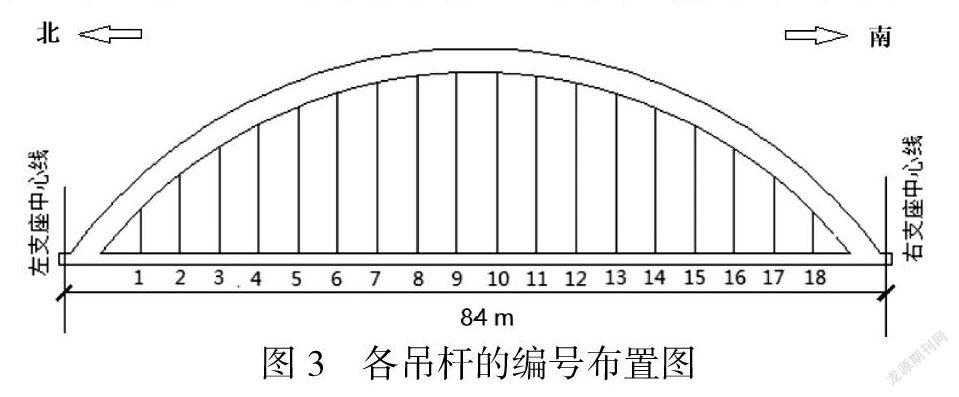
本次索力测试选定在空载和设计活载作用下，分别对东、西两侧的吊杆进行索力信息采集.同一根吊杆选取多个测试部分进行，最后选取一个测试索力值与理论索力对比.各根吊杆的编号布置见图2所示，现场测试仪器布置图如图3、图4所示.

6 索力综合分析

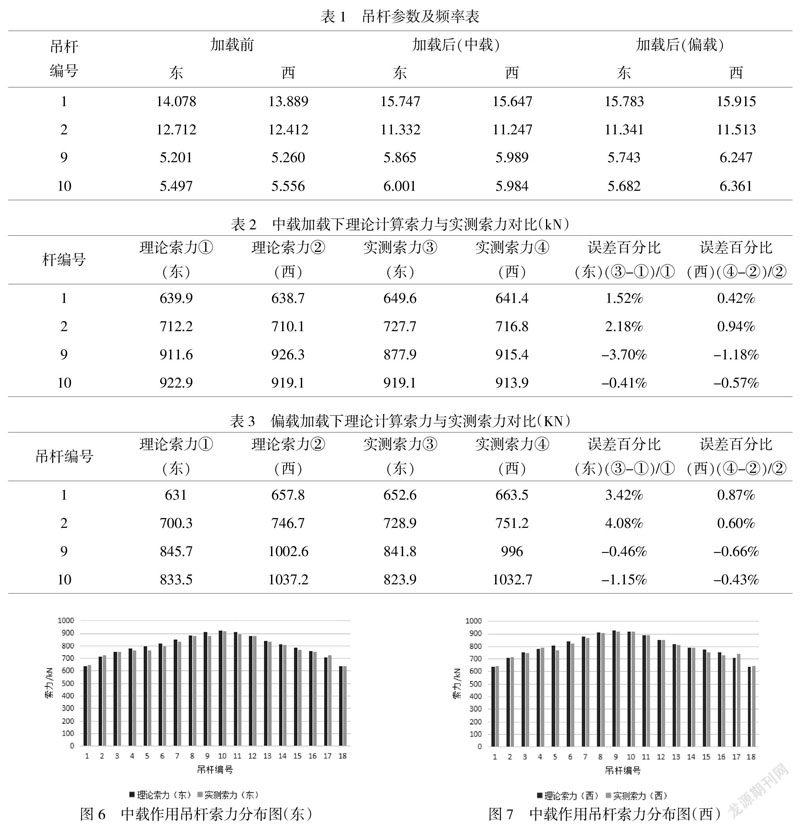
根据试验加载方案，对该桥段的吊杆拉力进行了多次测试与分析得到吊杆弦振动的频率实测结果和实测索力值，为了更清楚地了解索力加载前后的变化，将其部分吊杆数据列于表1、表2、表3.

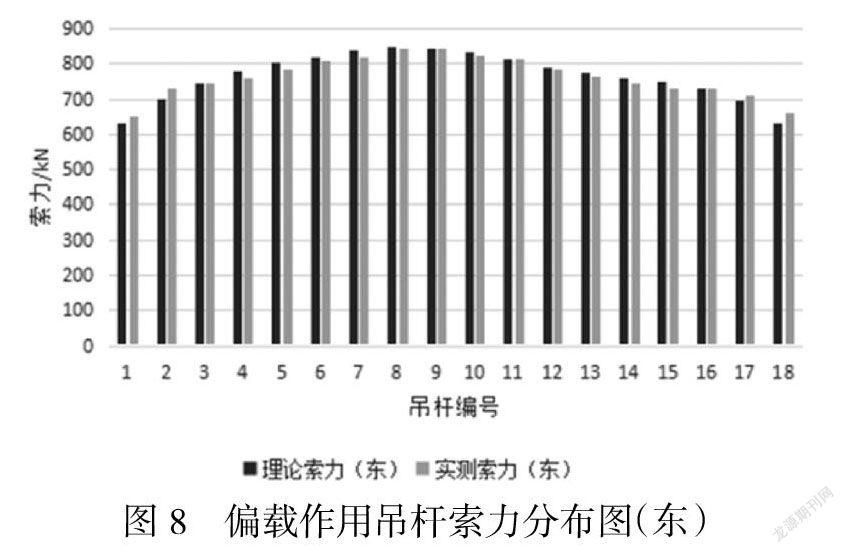
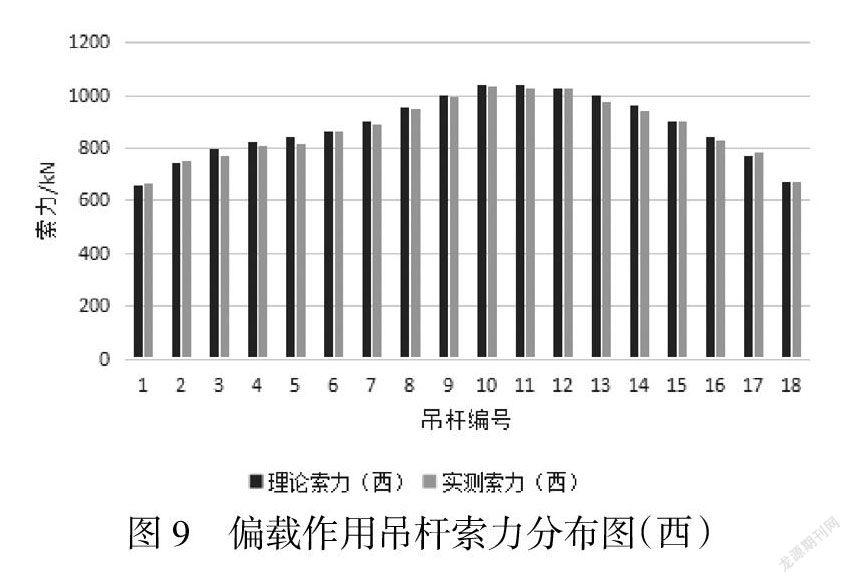
为了展现吊杆索力的走向趋势，以便更直观的观察，全部吊杆的索力值的分布情况见图6～图9.

经对表1、表2、表3以及图6～图9数据分析可得：

（1）中载加载作用下桥梁两侧相应位置的索力值存在着一定差异，两侧吊杆索力理论值与实测值误差百分比均小于5%，符合规范要求.在偏载加载作用下，桥梁加载一侧相应位置的索力值较大，两侧吊杆索力理论值与实测值误差百分比均小于5%，符合规范要求.

（2）通过频率法测试索力值的计算方法可知，索力与其自身的频率成反比.现场荷载作用下的数据和理论数据也反映了这一规律，充分体现了理论计算的准确性与科学性.

（3）该桥于1999年12月28日竣工通车，左、右幅桥梁吊杆在活载作用下索力变化不均匀，且试验活载采用的是设计活载（汽车-20级），但对于桥梁实际运营过程中的超载情况无法估计，加之本桥的交通量较大，造成吊杆疲劳，适应结构变形的能力较差.

7 结语

通过对哑铃型钢管混凝土系杆拱桥吊杆的检测研究，掌握全桥结构的现有工作状态，判断桥梁的实际工作状态是否符合现有相关规范要求，其检测结论可以为今后的养护提供技术参考，也可以为同类桥梁的评定提供参考依据.

参考文献：

〔1〕毛亚娜，刘世忠，叶丹.基于频率法对系杆拱桥吊杆索力测试的分析[J].兰州交通大学学报，2010，29（1）：124-128.

〔2〕陈阳，胡成.大跨度系杆拱桥吊杆索力测试研究[J].安徽建筑大学学报，2017，25（6）：24-29.

〔3〕李庭波.索力测试频率法的研究及其工程应用[D].长沙理工大学，2007.

〔4〕朱卫国，申永刚，项贻强，等.梁拱组合体系桥柔性吊杆索力测试[J].中南公路工程，2004，29（1）：21-23+36.

〔5〕宋一凡，贺拴海.公路桥梁荷载试验与结构评定[M].北京：人民交通出版社，2002.

〔6〕颉保平.某系杆拱桥索力测试方法及应用[J].甘肃科技纵横，2018，47（6）：48-50.

〔7〕吴晓亮.频率法在钢管混凝土吊杆拱桥索力测试中的研究与应用[D].合肥工业大学，2010.