基于可达性的轨道交通网络节点效率的计算

李艳涛　孙颖　周爱华　付晓

[摘要]轨道交通网络的运输效率决定着居民的出行满意度，合理地评价交通网络的效率具有重要的现实意义。在基于可达性的基础上，从乘客出行的时间成本角度，提出了一种计算节点效率的方法，并以北京市部分地铁站点为例进行验证计算，与传统的节点效率作对比分析。

[关键词]轨道交通网络;网络效率;节点效率

[中图分类号]U 239.5[文献标志码]A[文章编号]1005-0310（2019）04-0046-06

Calculation of Node Efficiency in Rail Transit Network

Based on Accessibility

Li Yantao，Sun Ying，Zhou Aihua， Fu Xiao

（College of Applied Arts and Science， Beijing Union University，Beijing 100191，China）

Abstract： The transportation efficiency of the urban rail transit network determines the satisfaction of the residents， so the reasonable evaluation of the efficiency of the transportation network is of great practical significance. Based on accessibility， this paper proposes a method to calculate the node efficiency from the perspective of the time cost of the passenger travel. Some of the subway stations in Beijing city are used as an example to verify the calculation， as a comparative analysis with the traditional node efficiency.

Keywords： Rail transit network; Network efficiency; Node efficiency

0引言

随着城市化进程的发展，城市交通问题日益加剧，公共交通作为城市交通的核心，承载着城市交通的主要运力。公共交通资源的合理化配置决定着居民的出行满意度。然而，目前的交通现状却存在许多问题，比如早晚高峰期的拥堵;公交、地铁站点间的客流量分布不均;乘客出行换乘次数多、换乘不方便等。如何改善这些交通状况是目前关注的热点问题。公共交通系统可以抽象为一个复杂的网络系统，

其中，站点为网络系统的节点，站点之间的公交线路、地铁线路可以视为节点间的边。从理论上讲，高效的公共交通系统不仅要满足覆盖性（所有居民在一定范围内对公交资源的可达性）要求，而且要具有较高的通达度，使居民的出行尽可能以最少的时间到达，从而实现出行效率最高。轨道交通是城市交通的动脉，其规划与运营直接影响人们出行的交通效率。地铁线路的布局与规划影响了出行效率，线路网络的布局不同，带来的出行体验也会不同，而评价线路布局的合理性，实际是对线路和站点构成的交通网络进行评价。合理的评价交通网络为提高人们的出行效率提供了理论基础。

自从复杂网络兴起之后，利用复杂网络分析和评价交通网络的研究逐渐开展起来。Latora验证了波士顿的地铁网络是个小世界网络[1]; Amaral等验证了航空网络是无标度网络[2]; Jiang实证分析了3个城市的道路网络具有小世界性[3];Sienkiewicz和Holyst[4]对波兰21个城市的公交网络的聚类系数、介数及匹配性等拓扑结构特性进行了分析，得出的结论是他们的度要么服从指数分布，要么服从幂律分布;王志如[5]建立了基于信息传递效率的聚类系数模型，构建了地铁网络小世界特性评价方法，验证了52个样本城市地铁网络具有小世界性。

在网络效率方面，Latora等定义了具有小世界性的复杂网络的传输效率，进而提出计算地铁效率的两个指标：全局效率和局部效率[6];周漩等[7]在全局效率的基础上定义了复杂网络中节点效率的计算指标;鲁放研究了基于供需匹配的网络运输效率[8]。综上所述，国内外对交通效率或运输效率的定义源于经济学的概念，一般指投入产出的比值或者运输服务水平，针对不同需要研究的交通对象其定义略有不同，考察标准和因素也不同。目前，关于道路路网的运输效率的文献较多，而对于城市轨道交通的交通网络效率的文献较少。现有的效率评价没有考虑网络的特征，没有考虑客流量;从运营机构角度出发，没有从乘客角度出发，缺少乘客全旅行时间这样的效用指标;仅仅反映出效率的最终表现，无法揭示效率的内涵，并进一步帮助优化效率。本文在Latora的全局效率和局部效率的基础上，改进了网络节点效率的定义，基于网络中的实际客流量流动性评价轨道交通网络的运输效率。

1网络效率的评价

交通网络具有复杂性。复杂网络的核心问题是复杂系统结构带来的功能影响问题，交通网络效率受网络拓扑结构的影响，因此，优化网络结构吸引了复杂网络领域很多学者的关注[9-10]。网络评价效率的指标有很多，在道路网络效率的研究中，已有文献使用多个指标来进行定性的评价和分析[11-13]，网络效率的定量研究有通過最短路径来评价[14]，也有通过综合的效率评价指标来评价[15]。节点与节点的相互关系构成了复杂网络，从而也确定了网络的运输效率，决定了网络特性[16]。Givoni和Rietveld[16]研究了荷兰铁路车站数量对乘客出行行为的影响。Jin等结合城市轨道交通车站客流及其网络拓扑度，研究了城市轨道交通车站的重要度，研究发现重要度高的车站均为换乘车站[17]。

评价复杂网络中节点重要性的方法很多，比如度中心性、介数中心性、紧密度中心性、节点效率等，但这些概念中的距离和度均来自图论的基本概念，反映了图中节点的拓扑属性。然而，在实际的交通网络中，途经节点的客流量和节点的地理位置都会影响节点在网络中的重要性。假设两个节点具有相同的度中心性或者介数中心性，如果通过两个节点的客流量大相径庭，则其重要性会截然不同。假设两个节点有相同的节点效率，如果两节点所处的地理位置具有不同的运输需求量，则两个节点的实际运输效率也是不同的。传统的节点效率反映了该节点到其他节点的难易程度，度量的依据是节点之间的拓扑距离，而实际的出行中，人们更关注时间成本。本文考虑了实际交通网络中的客流量和地理位置的因素，重新定义了网络全局效率和节点效率，量化了任意两个站点之间的出行时间成本。

1.1相关概念

设图G=（V，E）是一个无自环的无向网络，其中V={v1，v2，…，vn}是网络中所有节点的集合;E={e1，e2，…，em}且EV×V，是节点间边的集合。

定义1：节点距离是指两个节点之间最短路径上的边数，用dij表示。如果vi和vj之间不存在路径，则dij→∞。网络中任意两个节点之间距离的最大值称为网络的直径。

Latora在文献[6]中定义的全局效率也称为网络效率，定义如下。

定义2：网络效率E是指网络中所有节点对之间距离倒数之和的平均值，它用来表示网络信息流通的平均难易程度。

E=1n（n-1）i≠j1dij，

式中，n为网络中节点数目，dij为节点vi和vj之间的距离。

从网络效率E的定义可以看出，网络效率E表达了网络中所有节点对之间的平均接近程度。网络中节点对之间越接近、距离越短，网络效率值越大。网络效率越高，网络信息流通越容易。为了衡量网络中某一节点与其他节点的平均接近程度，依据网络效率的定义，文献[7]中定义了节点效率。

定义3：节点效率Ik是指节点vk与网络中其他节点之间距离倒数之和的平均值。

Ik=1n-1ni=1，i≠k1dki。

由节点效率Ik的定义可以看出，所有节点效率的平均值即为网络效率E，节点效率表达了该节点到网络中其他节点的平均难易程度。网络中节点效率越高，表明该节点向其他节点传输信息越容易、所消耗的资源越少。下文中称此节点效率为传统的节点效率。

1.2节点效率的定义

首先将轨道交通网络看做有向加权的网络。

定义4：定义有向网络G=（V，A，W），其中V={v1，v2，…，vn}为轨道交通网络中的站点，A为站点间的弧集合，W为弧集合上的权重。vi，vj∈V，如果vi→vj的客流量为wij，则定义其为vi，vj弧上的权重。

站点地理位置不同，会有不同的客流量。本文采用乘客的乘车时间来描述不同地理位置的站点客流量带给网络的差异性，重新定义轨道交通网络的全局效率和节点效率。

定义5：设轨道交通网络G=（V，A，W），其中V={v1，v2，…，vn}，定义网络的全局效率为E=ni=1nk=1wik·tikni=1nk=1wik，其中，wik表示vi进站vk出站的客流量，tik表示乘客wik所用的时间。

全局效率定义了交通网络中所有乘客乘车的平均时间，反映了网络中乘客的平均出行时间。E值越小，则网络的全局效率越高。

定义6：设轨道交通网络G=（V，A，W），其中V={v1，v2，…，vn}，定义网络中节点vk的节点效率为Ek=ni=1wik·tikni=1wik，其中wik表示vi到vk的客流量，tik表示乘客wik所用的时间;当i=k时，wkk表示站点vk的进站人数且tkk=1。

Ek的值越小，表示在實际的客流量中，乘客从其他节点到达节点vk所用的平均时间越少，认为网络中的乘客到达节点vk越容易。我们用Ek表示网络中的节点到达节点vk的难易程度，由于在轨道交通网络中，站点间的可达性具有相互性，即tik=tki，因此，可以用Ek描述节点vk运输乘客的效率。

2实证分析

2.1数据来源

2013年3月9号北京地铁全天的刷卡数据和2013年地铁线路数据。

2.2数据处理

由于数据源的局限性，选取了10号线之内的86个地铁站点。从IC刷卡数据中提取每一个出行者的出行路线（含路线所经过的站点），将出行者的进出站与地铁线路数据的起终点相匹配，将所有的出行者分类到这些线路中（一个起点一个终点对应一条线路），每条线路对应一个出行者，从而将每一条线路上的站点赋上一个时间值和一个客流量值，将时间值和客流量值做乘积，然后对同一站点的数据累加求和，得出途经该站点的客流量与时间成本乘积的总和。按照定义6和定义3计算86个节点的节点效率。

2.3节点效率对比分析

为了区别两个节点效率，下文中称定义6的节点效率为节点时间效率，定义3的节点效率为传统节点效率。

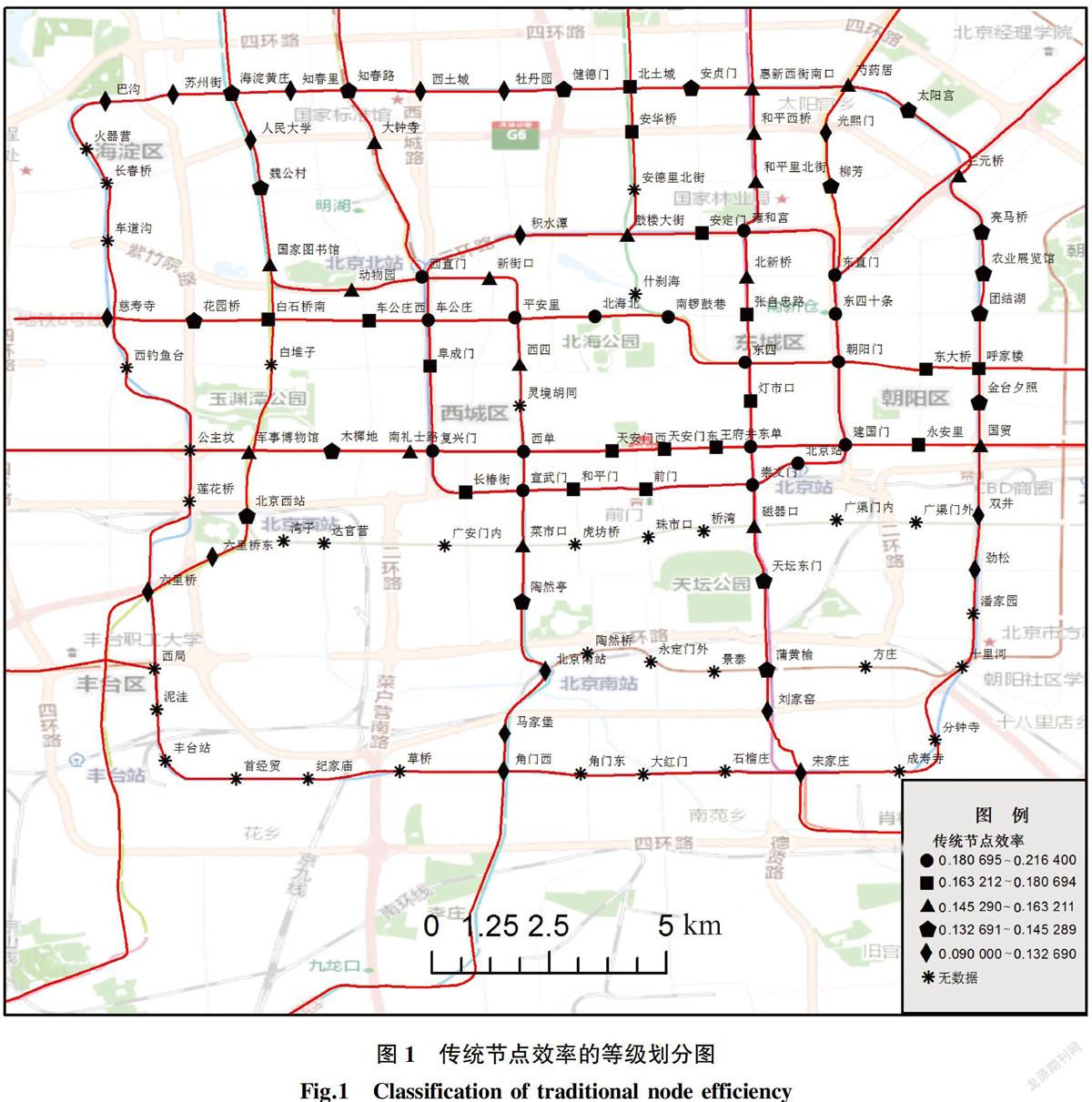
图1将站点的节点效率进行分级，17个圆点型站点的节点效率最高，其中15个站点是换乘站点。这意味着换乘站点比非换乘站点的节点效率高， 换乘站点到其他站点的平均距离更短。除此之外，传统节点效率和站点的地理位置有关，越是靠近地理位置中心的节点效率越高。10号线的传统节点效率（无数据的节点除外）普遍较高，是由于地理位置处于最外圈，受所选样本的局限性所致。

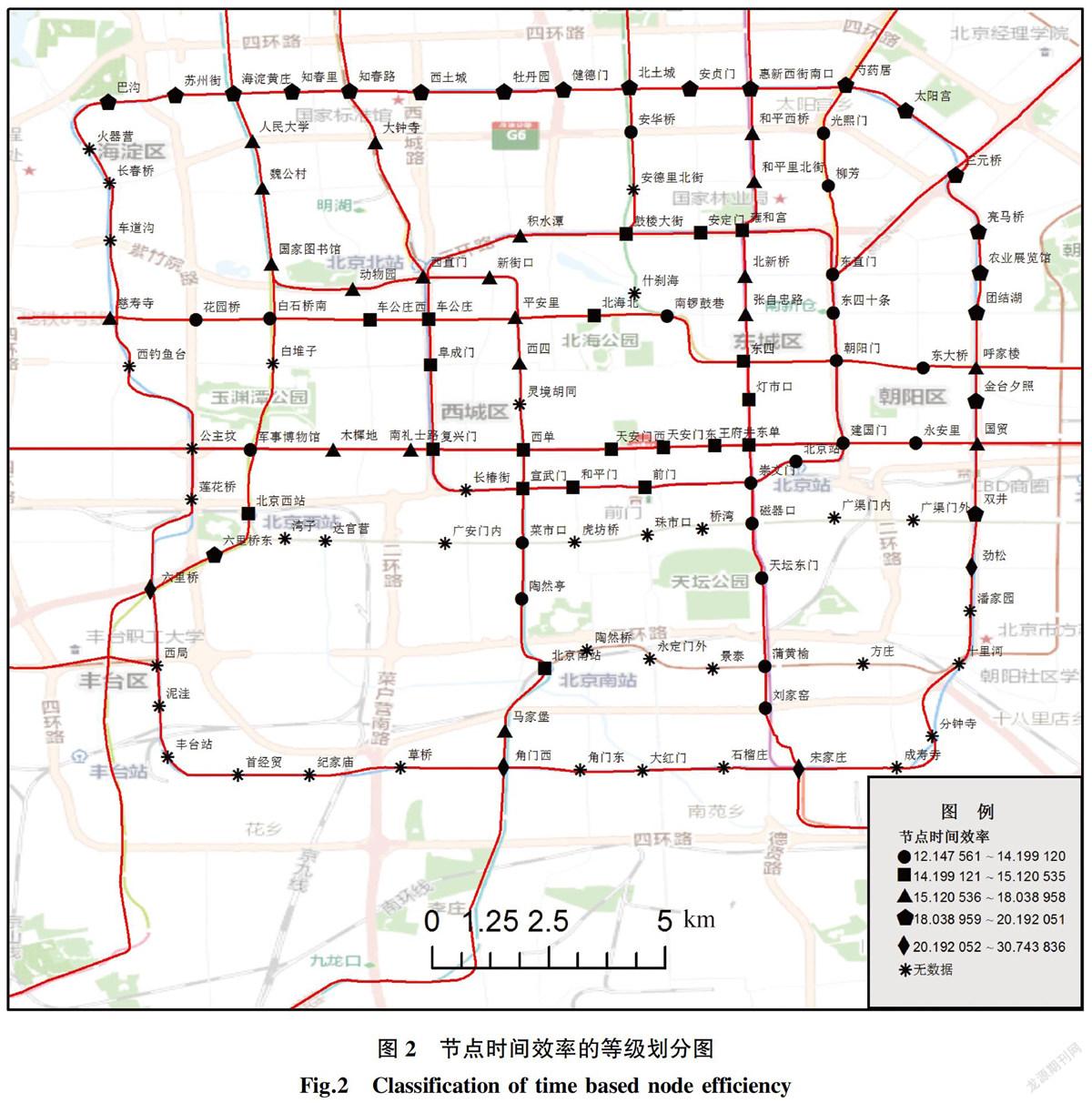
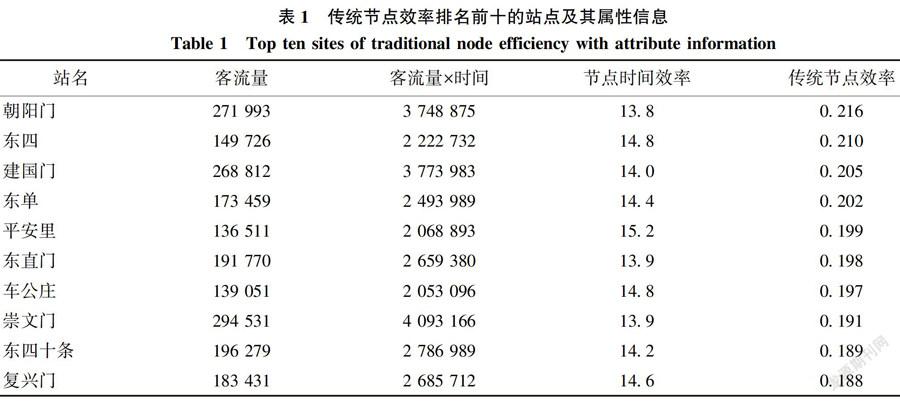
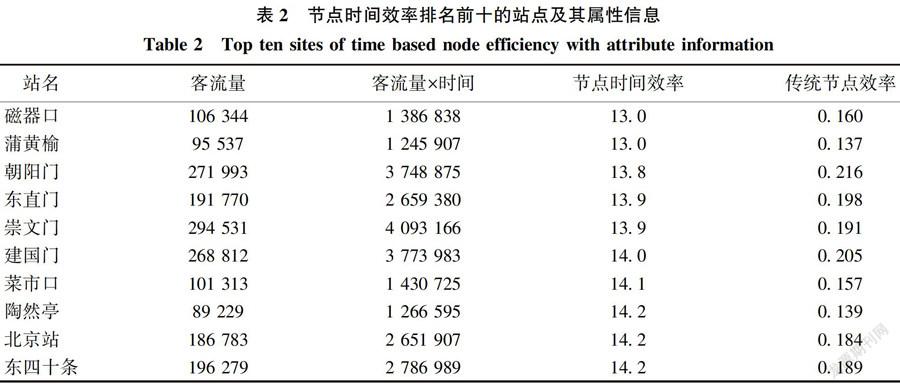
图2显示，圆点型站点的节点时间效率最高，21个圆点型站点中有6个节点是换乘站点，由定义可知，网络中的其他节点到这些站点的平均时间成本比较低。为了更好地对比传统节点效率与时间节点效率的不同，剔除10号线站点之后，本文分别选取了节点时间效率和传统节点效率排名前十的站点，分析其属性特征。见表1、表2所示。

通过对比表1和表2发现，朝阳门、建国门、东直门、崇文门和东四十条同时出现在两个表格中。东四、东单、平安里、车公庄和复兴门都是换乘车站，传统的节点效率排在前十名，可是它们的节点时间效率却并不是很理想，意味着人们到达这些换乘站点并不容易，目前的地铁线路设计并没有很好地满足客流量的分布需求。

3结束语

通过本文定义的网络全局效率和节点效率的计算公式，可以更客观地评价网络中所有出行乘客的平均出行时间和乘客抵达任意站点的平均时

间成本，丰富了评价站点效率的方法，实现了更全面地衡量网络的运营效率，通过改善节点效率低的站点，可以提高整个网络的效率，从而有针对性地为将来地铁线路的规划提供建议。

[参考文献]

[1]LATORA V，MARCHIORI M. Is the Boston subway a small world network[J]. Physica A， 2002（314）： 109-113.

[2]AMARAL L A N，SCALA A， BARTHELEMY M. Classes of behavior of small-world networks[J]. Proceedings of the National Academy of Sciences， USA， 1997（21）：11149-11152.

[3]JIANG B， CLARAMUNT C. Topological analysis of urban street networks[J]. Environment and Planning B：Planning and Design， 2004 （31）：151-162.

[4]SIENKIEWICZ J， HOLYST J A. Statistical analysis of 22 public transport networks in Poland[J]. Phys Rev E，2005（72）： 046127.

[5]王志如，苏国锋，梁作论.基于信息传递效率的地铁网络小世界特性评价[J].清华大学学报（自然科学版），2016，56（4）：411-416.

[6]LATORA V， MARCHIORI M. Efficient behavior of small-world networks[J]. Physical Review Letters， 2001，87（19）：1.

[7]周漩，张凤鸣，周卫平，等.利用节点效率评估复杂网络功能鲁棒性[J].物理学报，2012，61（19）：1-7.

[8]鲁放.城市轨道交通网络运输效率理论[D]. 北京：北京交通大学，2016.

[9]CARMI S， WU Z， HAVLIN S，et al. Transport in networks with multiple sources and sinks [J]. EPL （Europhysics Letters）， 2008， 84（2）： 28005.

[10]XUE Y， WANG J， LI L， et al. Optimizing transport efficiency on scale-free networks throug hassor tative or dissortative topology[J].Physical Review E， 2010，81（3）：037101.

[11]焦朋朋，陸化普，王建伟.基于交通效率的城市道路网络优化[J].清华大学学报（自然科学版），2005（3）：297-300.

[12]许良，高自友.基于路段能力可靠性的城市交通网络设计[J].中国公路学报，2006（2）：86-90.

[13]俞礼军，靳文舟.交通效率的度量方法研究[J].公路， 2006，25（10）： 102-106.

[14]秦进，史峰，邓连波，等.道路交通网络效率定量评价方法及其应用[J].吉林大学学报（工学版），2010，40（1）：47-51.

[15]GAO C， WEI D， HU Y， et al. A modified evidential methodology of identifying influential nodes in weighted networks[J]. Physica A： Statistical Mechanics and its Applications，2013，392（21）：5490-5500.

[16]GIVONI M， RIETVELD P. Do cities deserve more railway stations？ The choice of a departure railway station in a multiple-station region[J]. Journal of Transport Geography，2014（36）：89-97.

[17]JIN J， LI M， WANGY，et al. Importance analysis of urban rail transit network station based on passenger[J]. Journal of Intelligent Learning Systems and Applications，2013（5）：232.

（责任编辑李亚青）

[收稿日期]2019-03-05

[基金项目]校级人才强校项目（BPHR2019CZ02， BPHR2019CZ01）。

[作者简介]李艳涛（1981—），女，河北肥乡人，北京联合大学应用文理学院副教授， 主要研究方向为交通网络;孙颖（1971—），女，河北保定人，北京联合大学应用文理学院讲师，主要研究方向为城市地理;周爱华（1978—），女，山东东营人，北京联合大学应用文理学院副教授，主要研究方向为城市地理信息系统;付晓（1977—），女，四川金堂人，北京联合大学应用文理学院副教授，主要研究方向为城市遥感。E-mail： yantao@buu.edu.cn