两相位交叉口左转车辆抢行的元胞自动机模型
袁靓 吴戈 秦菲菲

摘要:为了解决道路两相位交叉口所存在的左转车辆抢行问题,避免造成严重交通冲突,首先分析了左转车辆抢行行为、路径抢行、以及与直行车辆到达冲突点的时间差相关的概率抢行,在考虑过街行人对抢行行为干扰的情况下,构建了车辆、行人耦合的双路径左转-直行冲突元胞自动机模型,通过计算机仿真分析研究了左转车辆抢行行为对交叉口通行能力的影响。结果表明,无过街行人时,左转车辆抢行使交叉口通行能力下降约5%;有过街行人干扰时,交叉口的通行能力则进一步降低10%~25%。研究结果可为提高道路交叉口服务水平、提高道路通行率和安全性决策提供参考。
关键词:公路运输;两相位交叉口;冲突;元胞自动机;抢行;行人
中图分类号:U4912文献标志码:Adoi: 10.7535/hbgykj.2019yx04002
Abstract:To solve the problem of left-turning vehicle preemption at two-phase intersection, avoid serious traffic conflicts,this study analyzes two preemption strategies of left-turning vehicle: path preemption,and probability preemption which is related to the time difference of straight vehicle reaching the conflict point.Then the research further considers the interference of pedestrians and constructes the pedestrians-vehicle double-path cellular automaton model. The influence of left-turning vehicle preemption behavior on the intersection capacity is studied through computer simulation.The results show that preemption reduce the traffic capacity of intersection by 5% without pedestrians, and in the case of pedestrians interference, it is further reduced by 10% to 25%. The research results can provide reference for improving the service level, access rates and safety of intersections.
Keywords:road transport; two-phase intersection; conflicting flow; cellular automaton; preemption; pedestrians
目前,对于两相位信号交叉口左转和直行车辆的冲突研究方法主要有交通流理论的参数解析法和微观仿真法,其前提条件是直行车辆具有绝对优先权。比如,SAYED等[1]调查了6种不同类型交叉口的基础数据,建立了平均冲突数和相关冲突流量乘积的线性回归冲突预测模型,较好地拟合了交叉口流量和直行左转冲突数之间的关系。戴霄等[2]、李淑庆等[3]根据两相位交叉口车流的运行特性,采用可穿越间隙理论对冲突车流进行模拟分析,得到了在直行优先条件下两相位交叉口的通行能力。李春艳[4]、冯军红等[5]考虑交通流特点,对HCM2000模型进行改进,提出了交叉口左转、右转的交通流延误模型。FOULAADVAND等[6]用元胞自动机模型研究无信号十字交叉口车辆冲突后发现,在低密度条件下,左转车辆让行机制有益于交叉口处理更多的流量。陈军华等[7]在研究中细化了交叉口内的元胞,引入了饱和车流、跟车模型和临界间隙理论,建立了只有直行和右转的十字交叉口元胞自动机模型,分析不同冲突流入率下交叉口的通行能力变化。范宏强等[8-9]以Nasch模型为基础,建立了考虑直行、左转与右转3种流量的T型交叉口元胞自动机模型,并加入防止车辆冲突死锁的机制,针对主干路车辆流入率及各车道转向车流对交叉口流量的影响进行分析研究。
在实际运行中,由于部分驾驶员左转时漠视让行规则,与直行车辆争夺通行权,存在极大的安全隐患。建立在直行车辆具有优先权基础上的分析在一定程度上能说明交叉口的冲突特性,却无法解释左转车辆抢行这一现实问题。BAI等[10]以左转车辆组为对象,研究非严格优先权及许可相位条件下的左转车辆交通流微观特性。马东方等[11]认为,在饱和条件下,无信号交叉口主路车流不再拥有绝对的优先权,因而改进了穿越间隙理论,研究了有限优先条件下设置交通信号的临界流量。宋现敏等[12]考虑了两相位交叉口左转车流对直行车辆优先权的影响,基于间隙理论建立了有限优先条件下的冲突延误模型。笔者利用元胞自动机模型建立两相位交叉口车辆冲突的仿真模型,并在冲突规则中加入左转车辆抢行和行人干扰因素,使其更符合实际运行。分析左转车辆抢行对交叉口通行能力的影响,可为提高交叉口服务水平和安全性提供参考。
1模型构建
元胞自动机模型能够灵活地引入描述真实交通条件的各种参量,有效模擬交通流中车辆的微观运动,便于研究车辆间的相互作用机理,因此在交通流理论的研究中得到了越来越广泛的应用[13]。如图1所示,本模型的研究对象是十字型交叉口以及相连的路段,各入口方向均设直行车道和左转车道,在机动车道两侧各有1条非机动车道和人行横道。为简化起见,暂不考虑右转车辆和非机动车,并假定该交叉口实行定时两相位信号控制。
1.1车辆运动更新规则
车辆运动模拟采用Nasch模型[14]。该模型规则简单,可以模拟许多交通现象,如自发产生的交通拥堵现象以及拥挤情况下的时走时停波[15]。在Nasch模型中,时间和空间是离散的,道路被划分为L个元胞,每一个元胞或被一辆车占据或未被占据。每辆车的速度只能是0,1,2,…,vmax(路段最大速度);当车辆进入交叉口时,最大速度限定为vmaxc,vmaxc≤vmax。
记xn和vn分别表示车辆n的位置和速度,dn为车辆n与前车(n-1)之间空的元胞数,sn为车辆n与前方交叉口之间的距离,p为随机慢化概率,车辆按照如下步骤更新运动。
Step1:加速vn→min(vn+1,vmax or vmaxc);
Step2:减速由于信号灯的存在,分为2种情况:
① 绿灯时,vn→ min(vn,dn);
② 红灯时,vn→ min(vn,dn,sn);
Step3:随机慢化以概率p,vn→ min(vn-1,0);
Step4:运动xn→xn+vn。
1.2左转车辆抢行行为
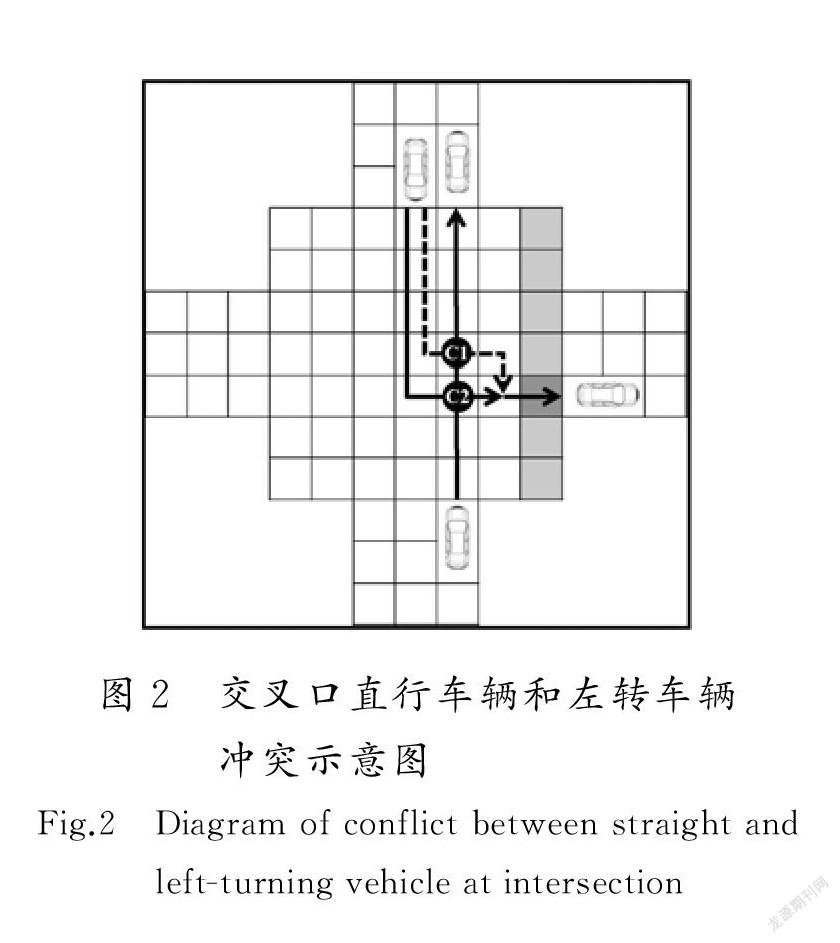
由于十字型交叉口的对称性,每个方向进口道的车辆运行方式相似,现选取南进口直行车辆和北进口左转车辆之间的冲突进行研究。
考虑左转车辆抢行时,交叉口内直行车辆和左转车辆存在C1和C2两个冲突点,相应的左转轨迹分别为路径1和路径2。设距离冲突点最近的直行车辆和左转车辆在下一时间步到达冲突点C1,C2的时间分别tS1和tL1,tS2和tL2。
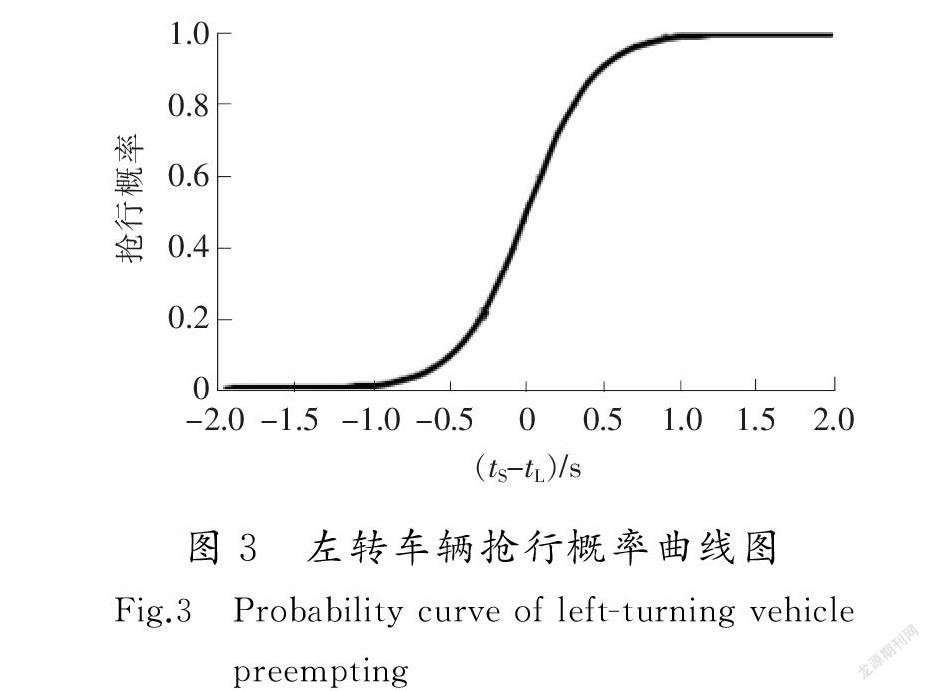
左转车辆驾驶员面对与直行车辆的冲突,需要权衡遵守交通法规、保证安全、尽快通过交叉口等因素,对抢行与否做出选择。抢行一般采取2种策略,一种是绿灯亮起后左转,抢在直行车辆前通过冲突点C1,可称为路径抢行;另一种是在2条左转路径上以某一概率p强行抢先通过冲突点,称之为概率抢行。以冲突点C2为例,若直行车辆和左转车辆下一时间步在C2发生冲突,按照离散选择模型(Discrete choice approach)理论[16],可以假定抢行概率p与直行车辆、左转车辆到达冲突点的时间差(tS2-tL2)成正比且服从Logistics型分布,如图3所示。
1.3直行车辆和左转车辆冲突规则
观察两相位交叉口内车辆的实际运行状况,可分以下几种情况考虑左转车辆和直行车辆的冲突。
1)tS1>1且tL1>1,即直行车辆和左转车辆在下一时间步都不会到达冲突点C1。此时,再判断两者是否同时到达冲突点C2。
①tS2>1且tL2>1,冲突点C2也不会有左转车辆和直行车辆同时到达的现象,两者按各自规则运行。
②tS2>1且tL2≤1,左转车辆按路径2运行也不发生冲突,所以选择路径2通过交叉口。
③ tS2≤1且tL2>1,左转车辆在下一时步不能到达冲突点C2,两车无冲突,按各自规则运行。
④tS2≤1且tL2≤1,左转车辆和直行车辆在冲突点C2处将要发生冲突,此时左转车辆根据图3的抢行概率p决定是否抢先通过冲突点C2。
2)tS1≤1且tL1≤1,直行车辆和左转车辆在下一时间步会在C1发生冲突,需进一步判断两车是否在冲突点C2发生冲突。
①tS2≤1且tL2>1,左转车辆在下一时间步不能到达冲突点C2,这时左转车辆沿路径1运行,以图3对应的抢行概率p占据或通过C1。若左转车辆出现抢行,则直行车辆在C1前减速或停车等待;反之,若左转车辆遵守让行规则,则在C1前减速或停车等待直行车辆的通过。
②tS2≤1且tL2≤1,左转车辆和直行车辆在冲突点C1和C2处都将发生冲突,此时分别计算(tS1-tL1)和(tS2-tL2)的值,对照图3的抢行概率,左转车辆选择抢行概率较大的路径运动。如果满足抢行概率要求,左转车辆抢先通过冲突点;反之,左转车辆在冲突点前等待直行车辆通过。
3)tS1>1且tL1≤1,左转车辆选择路径1提前转弯,抢先通过交叉口。
4)tS1≤1且tL1>1,左转车辆在下一时间步不会到达冲突点C1,判断能否选择路径2通过。
①tS2≤1且tL2>1,左转车辆也不能到达冲突点C2,直行车辆和左转车辆互不影响,分别运行。
②tS2≤1且tL2≤1,在冲突点C2处将发生直行与左转冲突,计算时间差值(tS2-tL2),左转车辆沿路径2以相应的概率抢先通过冲突点。
1.4行人更新规则
图2中灰色区域表示人行横道。人行横道上有南北双向的行人流,分别按泊松分布出现在行人区域两端,通过人行横道后,以概率1离开系统。行人的运动规则同样利用Nasch模型,以速度vp向前運动,在每个元胞内停留的时间为tp。每个元胞内行人数量不限。
1.5左转车辆和行人冲突规则
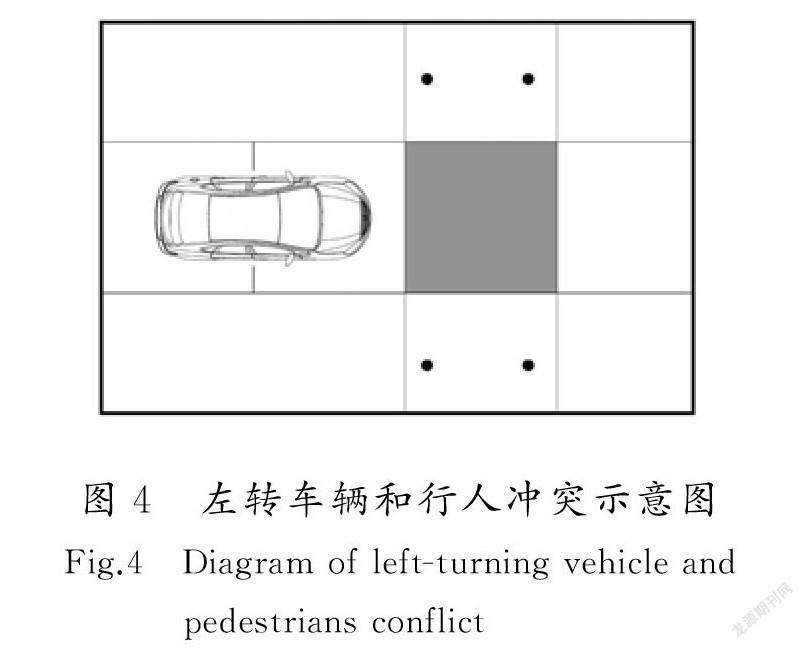
图4表示行人和左转车辆的冲突,冲突规则分为以下3种情况。
1)左转车辆的一部分已经在冲突区内,则行人在冲突区外等待。
2)冲突区内存在行人,则左转车辆在人行横道前等待。
3)冲突区虽还未被占用,但在下一步更新中车辆和行人都可能同时进入冲突区。根据交通规则,左转车辆遇过街行人时,为考虑行人的人身安全,一般会选择礼让行人,因此假定行人将以较大概率(p=0.8)优先占据冲突区域,此时车辆减速或停车等候。
2模拟结果
在计算机模拟中,设路段长度L为200个元胞,每个元胞的长度为3.6 m,每一辆车纵向占2个元胞。车辆在路段及交叉口的最高车速分别为vmax=5 cell/s(64.8 km/h)和vmaxc=3 cell/s(38.9 km/h),随机慢化概率p=0.2。行人的运动速度取vp=4.3 km/h,即3 cell/s。假定南北相位绿灯与红灯时长均为40 s。模型采用开放边界条件,车辆到达服从泊松分布,直行车辆与左转车辆的到达率分别为λS和λL。行人的到达率为λp,λp=0.05 人/s(180 人/h),系统模拟时长7 200步,步长1 s,为减少随机因素影响,取后3 600步进行数据统计。
2.1左转车辆抢行对交叉口流量的影响
首先在不考虑行人的条件下,比较本模型与单路径(路径2)直行优先Nasch模型的仿真结果。
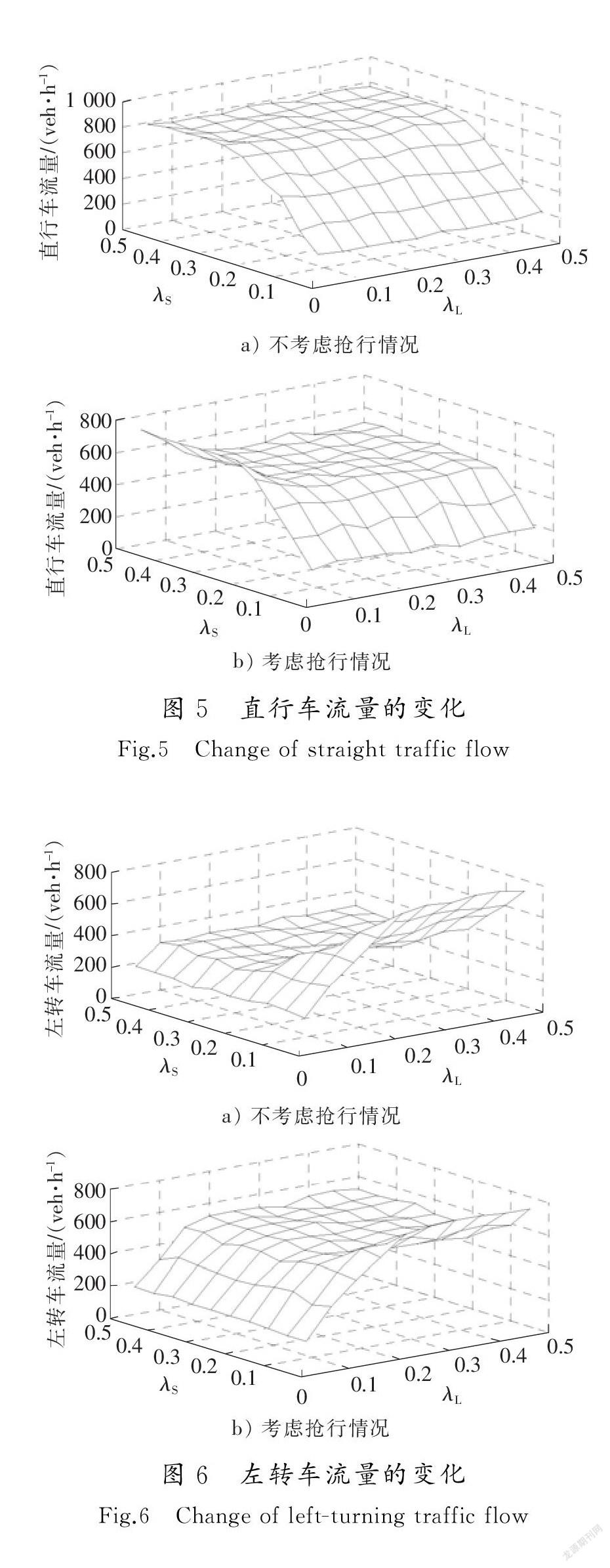
图5表示直行车流量的变化。在直行车辆绝对优先的情况下,无论左转车辆到达率λL如何变化,直行车辆通过交叉口的饱和流量都接近800 veh/h。如果考虑左转车辆抢行,直行车辆稳定饱和流量降至550 veh/h左右,减少了约250 veh/h;而且达到饱和流量的直行车辆临界到达率也由0.25 veh/s下降到0.15 veh/s。可见左转车抢行明显降低了交叉口的直行通行能力。
对比图6 a)和图6 b)的左转车流量变化,若直行车辆具有绝对优先权,左转车流量会随着直行车流量的增加而降低,当直行车辆与左转车辆的到达率分别大于0.25与0.1时,左转车流量降低形成一个低饱和流量值(300 veh/h)的平台区域。若考虑左转车辆抢行,左转车流量达到低饱和流量平台时的临界λS和λL分别为0.15和0.2,左转车饱和流量值增长到500 veh/h左右,大约增加200 veh/h,表明左转车辆抢行可以明显增大交叉口的左转车流量。
从交叉口总流量看,左转车辆不抢行与抢行时,交叉口总饱和流量分别为1 050 veh/h和1 000 veh/h左右,即左转车辆抢行会使整个交叉口通行能力降低约4.8%。图7表示不同到达率下左转车辆抢行造成的交叉口总流量的差值。在直行车辆较少而左转车辆较多的情况下,左转车辆抢行虽有略微增大交叉口通行能力的可能性,但当直行车辆较多而左转车辆较少时,少量的左转车辆抢行也会使交叉口直行车流紊乱,较大幅度地降低了交叉口通行能力。
2.2行人的干扰效果
在有左转车辆抢行的交叉口,由于同相位过街的行人存在,左转车辆即便能抢在直行车辆前通过冲突点,但仍不能通过交叉口,反而可能滞留在交叉口内,使直行车辆无法正常通过,导致交叉口通行能力进一步降低。
图8表示了左转车辆抢行条件下有、无过街行人情况的交叉口机动车总流量下降率的变化。可见,行人的干扰使交叉口总流量降低10%~25%,且进入系统的机动车数量越多,交叉口通过的机动车流量减少得越多。
2.3进一步的分析
下面从平均延误、排队长度等方面深入分析左转车抢行以及过街行人的干扰对交叉口运行状态的影响。
2.3.1对车辆延误的影响
图9 a)和图9 b)分别表示抢行与让行、以及有无行人情况下车均延误时间的差值。从图9 a)可以看到,在直行车和左转车流入率都很低的状态下,由于车辆冲突少,左转车抢行对整个交叉口车均延误的影响很小。在左转车流入率较小时,车均延误还会有一定降低,这是因为左转车辆可以灵活调整自己的位置,并以更快的速度通过冲突点。如果直行车流入率适中而左转车流入率大,左转车抢行导致更多直行车减速或停车等待,会增大车均延误时间。若两方向的车辆流入率都较大,则交叉口内流量到达饱和,左转车抢行依然会使平均延误时间增加20 s左右。
从图9 b)发现,增加行人干扰后,车均延误时间将明显增大,因为左转车为避让行人而在人行横道前排队,同时又阻碍直行车的通过,导致机动车延误时间急剧增大。
2.3.2对排队长度的影响
以直行车流入率λs =0.15 veh/s(540 veh/h)为例分析交叉口平均排队长度(每信号周期车辆最大排队长度的均值)以及平均停车车辆比(每周期通过停车线的车辆中有停车车辆的比例)随左转车流入率λL的变化,结果如图10和图11所示。
图10显示,在左转车流入率λL=0.15时,左转车抢行可以明显缩短每信号周期内左转车的平均排队长度,这当然是以增加直行车的排队长度为代价的。λL大于0.15后,左转车抢行并不能显著缩短左转车排队长度,而行人的存在将加剧交叉口机动车排队拥堵的程度。
2.3.3对停车比例的影响
由图11可见,如果左转车辆不抢行,那么直行车辆的停车车辆比为60%~70%。λL>0.15后,2个方向的车辆流入率均很大,超过交叉口的通行能力,所有机动车都需要至少停车一次才能通过交叉口。在有过街行人的情况下,左转车辆抢行迫使所有通过交叉口的直行车辆在更小的左转车辆流入率(λL=0.1)时就必须至少停车1次。
2.3.4对抢行和路径选择比例的影响
如图12给出了抢行左转车辆的比例及其行驶路径的变化。无行人時,60%~65%的左转车辆会抢行,而有行人时,抢行左转车辆的比例降至50%~55%。可见行人的干扰减少了左转车辆的抢行。因为左转车辆在人行横道前减速停车等待行人通过,造成后续左转车辆不能再有效地抢行。
左转车辆选择路径1的比例基本都高于50%,因为路径1既可以提前左转,又可以以概率抢行。在有行人干扰的情况下,选择路径1左转的比例略低于无行人时,显然是因为路径1上已经有让行行人的左转车辆在停车等待了。
3结论
本文利用元胞自动机Nasch模型,重点考虑左转车辆抢行,通过基于两股车流到达冲突点的时间差变化的Logisitic型抢行概率以及多左转路径选择,细化了左转车辆的行驶行为,并在此基础上加入行人干扰因素,建立了更加符合实际交通状况的两相位交叉口直行-左转机动车-行人冲突模型。结果表明,左转车辆的抢行行为对左转车辆快速通过交叉口有一定的作用,但是却严重妨碍了直行车的运行,最终导致交叉口的通行能力降低5%左右。而行人的加入强化了这一结果,使得交叉口通行能力进一步下降10%~25%。研究虽然取得了一定成果,但是,左转车辆在交叉口内的运动轨迹复杂多样,两条运行路径还不足够,且本文左转车辆驾驶员行为选择具有一致性,而行为选择会受到个人属性的影响,对于这些问题,还有待进一步研究。
参考文献/References:
[1]SAYED T,ZEIN S.Traffic conflict standards for intersections[J]. Transportation Planning and Technology, 1999, 22(4):309-323.
[2]戴霄,陈学武.可穿越间隙理论求解二相位交叉口通行能力[J]. 交通运输工程与信息学报, 2005, 3(4):70-74.
DAI Xiao, CHEN Xuewu. Calculation method for the capacity of two-phasebit intersections based on critical gap theory[J].Journal of Transportation Engineering and Information, 2005, 3(4):70-74.
[3]李淑庆, 谢晓忠, 邬贵冬. 城市道路两相位交叉口左转车道通行能力研究[J]. 重庆交通大学学报(自然科学版), 2010, 29(5):745-749.
LI Shuqing, XIE Xiaozhong, WU Guidong. Capacity analysis on left-turn lane at two-phase intersection of urban road[J]. Journal of Chongqing Jiaotong University(Natural Science), 2010, 29(5):745-749.
[4]李春艳. 信号交叉口左右转交通流延误模型研究[D]. 北京:北京工业大学, 2004.
LI Chunyan. Research on Delay Model of Left-turning and Right-Turning Traffic Flow at Signalized Intersection[D]. Beijing: Beijing University of Technology, 2004.
[5]冯军红, 贺尔铭, 张文刚. 两相位信号交叉口左转交通流延误模型的研究[J]. 交通信息与安全, 2009, 27(1):75-78.
FENG Junhong, HE Erming, ZHANG Wengang. Study of a model for left-turn flow delay at two-phase signalized intersection[J].Journal of Transport Information and Safety, 2009, 27(1):75-78.
[6]FOULAADVAND M E, BELBASI S. Vehicular traffic flow at a non-signalised intersection[J]. Traffic and Granular Flow’07,2007, 40(29):82-89.
[7]陳军华, 张星臣, 赵凛,等. 基于元胞自动机的交叉口仿真平台研究[J]. 交通运输系统工程与信息, 2009,9(1):68-73.
CHEN Junhua, ZHANG Xingcheng, ZHAO Lin, et al. Simulation platform for non-signalized intersection based on cellular automation[J].Journal of Transportation Systems Engineering and Information Technology, 2009,9(1):68-73.
[8]范宏强, 贾斌, 李新刚,等. 无信号T型交叉口交通流特性研究[J]. 交通运输系统工程与信息, 2012, 12(1):185-192.
FAN Hongqiang, JIA Bin, LI Xingang, et al. Characteristics of traffic flow at non-signalized T-shaped intersection[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(1):185-192.
[9]范宏强. 基于元胞自动机的若干类型城市道路交叉口交通流特性研究[D]. 北京:北京交通大学,2015.
FAN Hongqiang. Research on the Traffic Flow Characteristics of Urban Road Intersection Based on Cellular Automaton Model[D].Beijing: Beijing Jiaotong University, 2015.
[10]BAI Qiaowen, CHEN Yongheng, QU Zhaowei, et al. Nonstrict priority left-turning maneuvers with a permitted phase at signalized intersections: Empirical study in China[J]. Journal of Transportation Engineering, Part A: Systems, 2017, 143(3):04016009.
[11]马东方, 王殿海, 杨希锐,等. 有限优先下交叉口信号设置的临界流量依据[J]. 东南大学学报(自然科学版), 2010, 40(4):860-865.
MA Dongfang, WANG Dianhai, YANG Xirui, et al. Critical traffic volume of traffic signal warrant under limited priority condition[J].Journal of Southeast University(Natural Science Edition), 2010, 40(4):860-865.
[12]宋现敏, 孙锋, 王殿海. 两相位交叉口车辆冲突延误模型[J]. 吉林大学学报(工学版), 2009, 39(2):326-330.
SONG Xianmin, SUN Feng, WANG Dianhai. Conflict delay models at two-phase intersection[J].Journal of Jilin University (Engineering and Technology Edition),2009, 39(2):326-330.
[13]唐夕茹, 徐丽萍. 基于改进型元胞自动机模型的双车道公路交通冲突分析[J]. 公路交通科技, 2016, 33(3):110-115.
TANG Xiru, XU Liping. Analysis of traffic conflict in two-lane highway based on improved CA model[J]. Journal of Highway and Transportation Research and Development, 2016, 33(3):110-115.
[14]KAI N, MICHAEL S. A cellular automaton model for freeway traffic[J]. Progress of Theoretical Physics, 1992, 2(12):2221-2229.
[15]賈斌,高自友,李克平,等. 基于元胞自动机的交通系统建模与模拟[M].北京:科学出版社, 2007.
[16]UNCLES M D. Discrete choice analysis: Theory and application to travel demand[J]. Journal of the Operational Research Society, 1987,38(4):370-371.

