多棒结构磁致伸缩换能器的磁场研究

李亚芳 王博文 黄文美

摘要 基于换能器的不同应用背景，设计了2台换能器样机，分别为应用于高频的双棒结构换能器样机和应用于微米级抛光的四棒结构换能器样机。基于Maxwell方程组，应用有限元方法对两台多棒结构换能器样机进行了磁场分析，确定了最佳磁路结构。研究发现，在6 000 Hz频率和2 A励磁电流下，驱动线圈串联的双棒结构换能器的平均磁通密度为0.879 T。与其他磁路结构相比，它的磁通密度更高且更均匀，适用于高频换能器。对四棒结构换能器进行不同激励条件下的磁场分析，结果可知A棒和C棒的磁通密度相位相差180°，B棒和D棒的磁通密度相位也相差180°，磁通密度峰值均为0.45 T。4个磁致伸缩材料棒之间形成闭合回路，漏磁较小，具有三维位移输出，此磁路结构适用于微米级抛光的换能器。

关 键 词 磁致伸缩换能器;多棒结构;磁场分析;磁路优化;结构设计

中图分类号 TN712.2     文献标志码 A

Abstract Based on the different applications of transducer， two transducer prototypes are designed：  two magnetostrictive rods transducer for high frequency applications and four magnetostrictive rods transducer for micron polishing. Based on Maxwell equations， the magnetic field of the two transducers is analyzed by finite element method， and the optimal magnetic circuit structure is determined. It is found that the average flux density of the two magnetostrictive rods transducer with driving coils in series is 0.879 T at 6000 Hz frequency and 2 A exciting current. Compared with other magnetic circuit structures， its flux density is higher and more evenly distributed， which is suitable for high frequency transducers. The magnetic field of the four magnetostrictive rods transducer under different exciting conditions is analyzed. The results show that the phase difference of the magnetic flux density of rod A and rod C is 180°， that of rod B and rod D is also 180°. The peak values of magnetic flux density of the four rods are 0.45 T. A closed loop is formed between the four magnetostrictive rods. This magnetic circuit structure has a small magnetic flux leakage. The transducer has three-dimensional displacement output. The magnetic circuit structure is suitable for the micron polishing transducers.

Key words magnetostrictive transducer; multi-rods; magnetic field; magnetic circuit optimization; structural design

0 引言

磁致伸縮换能器是一种将电磁能转化成机械能的电磁器件，在超精密加工、微型机电系统和精密抛光等军事和工业领域中具有广泛应用[1-2]。磁致伸缩换能器的核心元件为磁致伸缩材料，主要包括Terfenol-D和Galfenol。Terfenol-D的优点是具有较大的磁致伸缩量（～1.6×10-3）。Galfenol的优点是在很低的磁场强度（～8 kA/m）下具有中等的磁致伸缩（～3.5×10-4），磁滞特性较小，表现出较高的拉伸强度（～500 MPa）。根据磁致伸缩换能器的不同用途选用不同的磁致伸缩材料作为核心元件。磁致伸缩换能器的输入和输出响应是评价磁致伸缩换能器性能的重要指标[3-4]。其中研究磁致伸缩换能器的输入最重要的是分析磁致伸缩换能器的磁场。传统的磁致伸缩换能器的核心元件为单根磁致伸缩材料棒[5]，文献[6]以Terfenol-D材料作为驱动元件的换能器为研究对象，采用有限元软件ANSYS对换能器的材料的选择及结构尺寸进行优化分析。文献[7]以Galfenol材料作为驱动元件的换能器为研究对象，分析了磁致伸缩换能器的输入与输出关系。基于非线性离散能量平均模型对Galfenol材料进行建模。该模型同时考虑了磁致伸缩换能器中涡流、漏磁、结构动力学和非线性材料行为的影响。文献[8]研究了磁致伸缩换能器的磁设计，对线圈结构尺寸和磁路元件的选择对换能器磁场特性和输出位移的影响进行了分析、优化及有限元仿真，并对换能器的磁路损耗和气隙进行了相关的研究。文献[9]对磁致伸缩换能器进行了磁路的优化和仿真。设计了闭磁路系统，分析了偏置磁场对磁致伸缩棒磁场强度的均匀分布的影响。同时得出了磁致伸缩换能器的最佳电流驱动密度。文献[6-9]对传统的磁致伸缩换能器的磁场进行了有限元分析，优化了磁路结构。本文对本课题组所研发的两台换能器样机进行了磁场分析，两台样机分别为应用于高频的双棒结构磁致伸缩换能器和应用于微米级抛光的具有三维输出的四棒结构磁致伸缩换能器。确定了两台换能器的最佳磁路结构，此外通过磁场分析确定了换能器的最佳偏置和最佳激励条件，为进一步研究换能器的输出响应提供理论基础。

1 双棒结构磁致伸缩换能器

双棒结构磁致伸缩换能器的结构和样机如图1所示。其工作原理为：在换能器的驱动线圈中通入交流电流，产生交变磁场。磁致伸缩棒在交变磁场的作用下发生轴向的伸缩，将电磁能转换成机械能。以振动的形式来推动变幅杆运动，实现位移和力的输出。此磁致伸缩换能器的应用背景为高频、大输出力和大功率，因此选用Terfenol-D作为核心元件。双棒结构磁致伸缩换能器的输出力是单棒结构磁致伸缩换能器输出力的二倍。换能器的结构确定为两个Terfenol-D棒（直径为15 mm、长度为102 mm）、两个驱动线圈（每个线圈150匝）、碟形弹簧、调节螺母、变幅杆、磁轭和外壳。此换能器的工作频率为5 000～7 500 Hz。为了减少Terfenol-D棒在高频工作条件下的涡流损耗，每个Terfenol-D棒被加工成1 mm的薄片，然后用环氧树脂胶粘合在一起。两个Terfenol-D棒与磁轭之间连接形成闭合磁路，可以减小漏磁。驱动线圈同时为Terfenol-D棒提供偏置磁场和激励磁场。偏置磁场用来抑制Terfenol-D棒的倍频效应。碟形弹簧和调节螺母为Terfenol-D棒提供最佳的预应力。

1.1 换能器的磁场模型

式中n是边界表面的法线向量。通过公式（1）～（5）建立了换能器的磁场控制方程。基于控制方程，利用有限元软件COMSOL Multiphysics对换能器的磁场进行了有限元计算[13-14]。初始值和边界条件为[At=0=0]，[ ∂VA：A=A*]。其中[A*]为给定值。在COMSOL Multiphysics有限元软件中建立磁致伸缩换能器的三维几何模型。Terfenol-D棒的主要材料性能选为B-H曲线，其中重要的材料参数为饱和磁致伸缩系数[λS]= 1.6×10-3，杨氏模量E = 3×1010 Pa，泊松比v = 0.45。同时添加两个驱动线圈、碟形弹簧、调节螺母、变幅杆、磁轭和外壳的材料参数。磁致伸缩换能器的外部由空气域包围。在空气域的外部边界，磁矢势A=0。Terfenol-D棒在电磁场中遵循安培定律。加入多匝线圈项为驱动线圈提供了激励条件。在结构力学中，Terfenol-D棒选择“磁致伸缩材料”模块，边界选择固定约束和边界载荷。

1.2 双棒结构磁致伸缩换能器磁路结构设计

设计磁致伸缩换能器磁路结构的目的是在相同激励条件下提高Terfenol-D棒的磁通密度和磁通密度的均匀性，减少漏磁，进而减小磁路的损耗。因为漏磁会引起磁致伸缩换能器激励电流的严重畸变，导致驱动线圈不能给磁致伸缩换能器提供所需要的磁场[15-16]。

图2为单棒结构磁致伸缩换能器和双棒结构磁致伸缩换能器的磁路结构[17]。它主要由磁轭和Terfenol-D棒组成。在磁轭和Terfenol-D棒的截线位置处选取磁通密度数据进行磁场分析。对双棒结构磁致伸缩换能器的两个激励线圈进行并联连接和串联连接的磁路进行磁场分析，确定最佳连接方式。

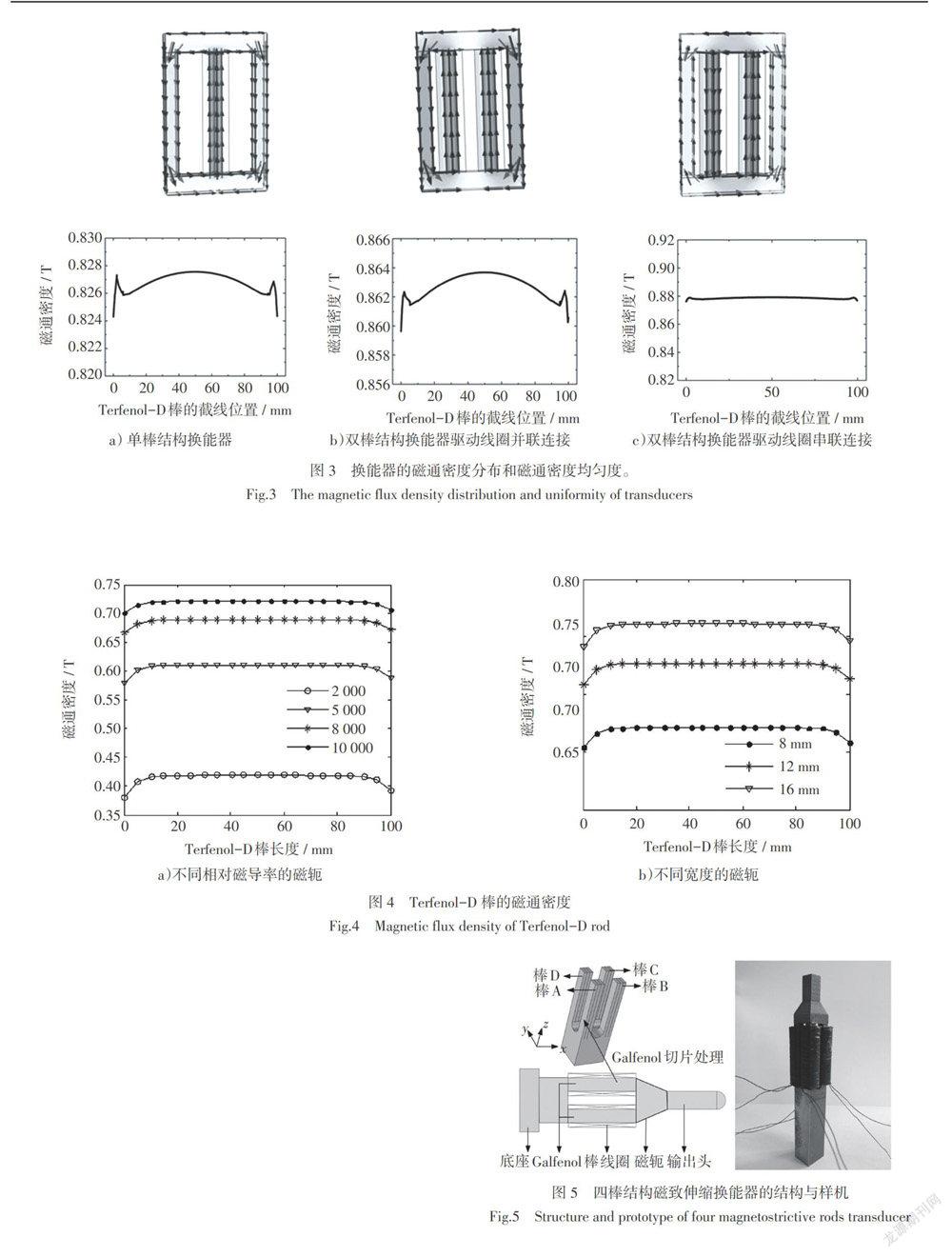
图3 a）～c）分别为单棒结构换能器磁路结构、双棒结构换能器驱动线圈并联连接磁路结构和双棒结构换能器驱动线圈串联连接磁路结构的磁通密度分布云图。图中箭头代表了磁通的方向。在6 000 Hz频率和2 A励磁电流下，单棒结构换能器的平均磁通密度为0.827 T，驱动线圈并联的双棒结构换能器的平均磁通密度为0.863 T，驱动线圈串联的双棒结构换能器的平均磁通密度为0.879 T，由此可知驱动线圈串联的双棒结构换能器的磁路结构的平均磁通密度比其他结构更高。图3还分别给出了Terfenol-D棒的截线位置的磁通密度。结果表明在Terfenol-D棒的中心位置磁通密度均匀，但是Terfenol-D棒两端的磁通密度较不均匀。通过3种磁路结构中Terfenol-D棒的中心位置的磁通密度比较，发现驱动线圈串联的双棒型换能器的磁路结构的磁通密度均匀性最高。此外对换能器的磁场分析需要考虑漏磁，当磁轭中的磁通密度越大时，空气中的漏磁通就越小。本文计算了磁轭的截线位置的磁通密度。单棒结构换能器的磁轭最大磁通密度为0.75 T，双棒结构换能器的磁轭最大磁通密度为1 T。可知双棒结构的漏磁比单棒结构的漏磁小。综上所述，与传统的单棒结构换能器相比，驱动线圈串联连接的双棒结构换能器的磁路結构更适合于具有高频激励、大输出力和大输出功率需求的换能器。

在磁致伸缩换能器磁路结构设计中，磁轭的材料和结构会影响Terfenol-D棒的磁通密度。因为不同材料的磁轭具有不同的相对磁导率，影响磁力线的分布。磁轭的材料通常为镍铁（相对磁导率ur =2 000）、Q235钢（ur =4 000～5 000）和硅钢片（ur =7 000～10 000）等。图4分析了不同相对磁导率的磁轭和磁轭的不同结构对Terfenol-D棒磁通密度的影响。当磁轭的相对磁导率分别为2 000、5 000、8 000和10 000时，Terfenol-D棒的磁通密度分别为0.42 T、0.61 T、0.69 T和0.72 T。其原因是磁轭的磁阻随相对磁导率的增加而减小。因此磁致伸缩换能器选用相对磁导率较高的硅钢片作为磁轭的材料。所设计的磁致伸缩换能器样机中Terfenol-D棒的直径为15 mm。当磁轭宽度为8 mm时，Terfenol-D棒的磁通密度为0.67 T，当磁轭宽度增加到16 mm时，Terfenol-D棒的磁通密度增加为0.76 T。由此可知磁轭宽度越大，空气中漏磁通越小。因此，增大磁轭的宽度有助于增加Terfenol-D的磁通密度从而改善磁致伸缩换能器的输出特性。从仿真结果可知磁轭宽度应选为16 mm。但是过度增大磁轭的宽度会对谐振频率产生影响。综合分析，磁轭宽度选为16 mm。磁轭的长度选为60 mm。

2 四棒结构磁致伸缩换能器

四棒结构磁致伸缩换能器的结构和样机如图5所示。换能器由4个Galfenol棒（逆时针标记为棒A、棒B、棒C和棒D）、4个驱动线圈、底座、磁轭和输出头组成。对立方体的Galfenol原材料进行线切割加工得到4个完全对称的Galfenol棒（4 mm×4 mm×34 mm）。同样为了减少涡流损耗的影响，将Galfenol棒加工成1 mm的薄片，并用环氧树脂胶粘合在一起。四棒结构磁致伸缩换能器所需要的驱动磁场为5 kA/m。由此可知每个线圈为300匝，电阻为1.7 Ω，偏置电流为0.3 A，激励电流为0.2 A。

2.1 四棒结构磁致伸缩换能器的工作原理

四棒结构磁致伸缩换能器的工作原理为：磁致伸缩换能器的输出头的运动轨迹由4个Galfenol棒的驱动磁场控制。当给4个Galfenol棒施加相同的方向的激励电流，4个Galfenol棒同时伸长或缩短，磁致伸缩换能器产生轴向的输出位移。当给一对相对的线圈（A和C，B和D）提供180°相位差的驱动电流时，两个Galfenol棒的运动状态相反，同时给相邻线圈（A和B）提供一定相位差的驱动电流时，输出头可以产生三维位移[18-20]。

根据磁致伸缩换能器的设计理论，电路和磁路理论，确定了4个Galfenol棒的驱动电流：

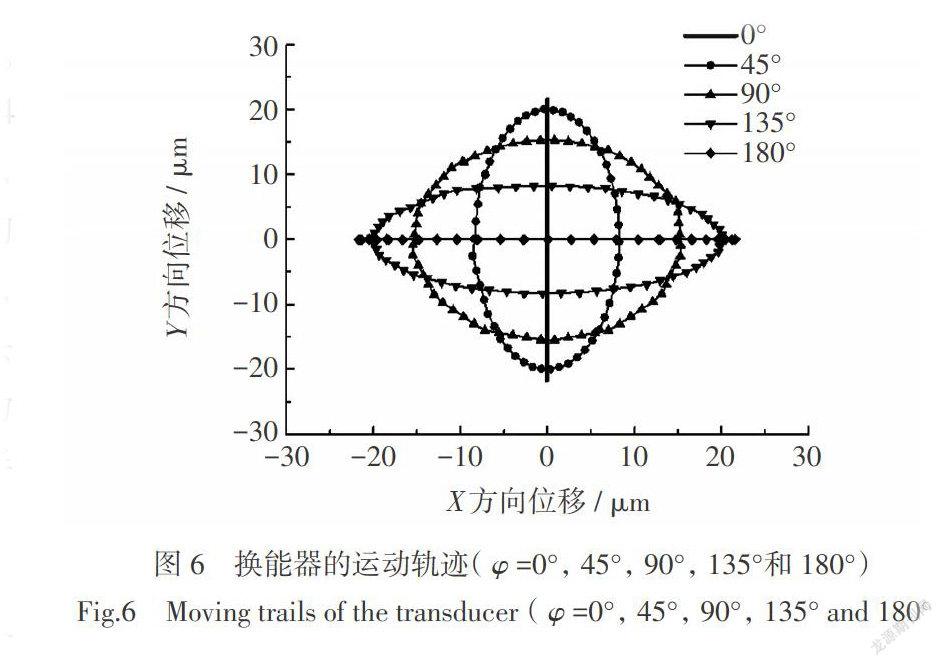
根据式（6）对4个Galfenol棒提供不同的驱动电流，可使换能器的输出头产生三维位移输出。图6为换能器在二维平面内的输出位移轨迹图。4个Galfenol棒的驱动电流中的[φ]分别为0°，45°，90°，135°和180°。当[φ]为0°和180°时，输出头的运动轨迹呈直线。换能器的输出振幅可达23 μm，最大位移为46 μm。当[φ]为45°和135°时，输出头的运动轨迹为椭圆轨迹，两个半轴的位移分别为21 μm和8 μm。当[φ]为90°时，输出头的轨迹为半径为15 μm的圆。

2.2 四棒结构磁致伸缩换能器的磁场分析

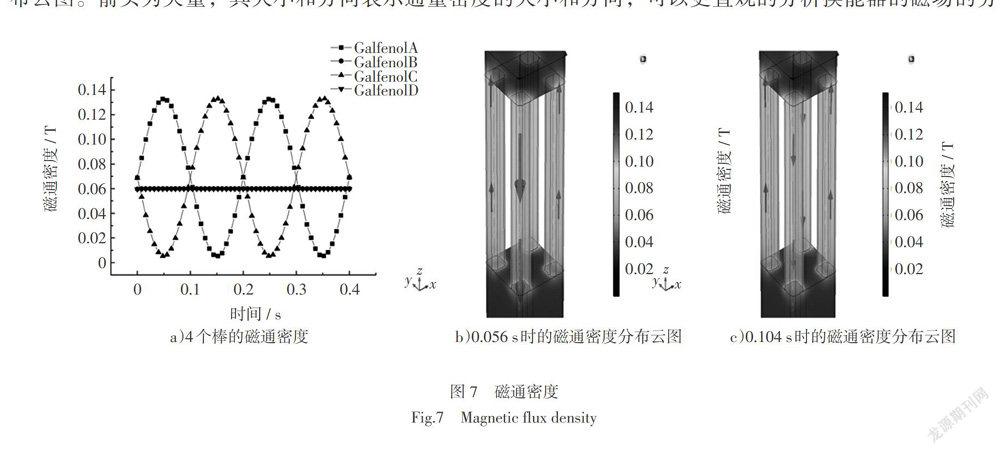
当一对相对的棒（棒A和棒C）工作时，每个棒所提供的驱动电流分别为[IA=0.3+0.2sin（2πft），][ IB=0，  IC=0.3+0.2sin（2πft+180∘），  ID=0]。4个Galfenol棒中心处的磁通密度如图7所示。A棒和C棒的磁通密度峰值为0.13 T，A棒和C棒的磁通密度相差180°。B棒和D棒的磁通密度稳定在0.06 T，通过分析可知4个Galfenol棒之间形成了闭合磁路。而且漏磁很小。与传统的磁致伸缩装置相比，4个Galfenol棒之间形成了闭合磁路，简化了换能器的结构，而且使换能器具有良好的散热性能。图7 b）和图7 c）为在0.056 s（1/4周期）和0.104 s（1/2周期）时换能器的磁通密度分布云图。箭头为矢量，其大小和方向表示通量密度的大小和方向，可以更直观的分析换能器的磁场的分布。图8为4个Galfenol棒同时工作时，4个Galfenol棒中心处的磁通密度。每个Galfenol棒所提供的驱动电流为[IA=0.3+0.2sin（2πft），][ IB=-0.3+0.2sin（2πft+π4），][ IC=0.3+0.2sin（2πft+π）， ][ID=-0.3+0.2sin（2πft+5π4）]。

结果可知4个棒中心处的磁通密度随时间发生正弦变化，A棒和C棒的磁通密度相位相差180°，B棒和D棒的磁通密度相位相差180°， 磁通密度峰值均为0.45 T。综上所述，根据所提供的驱动电流，此四棒结构磁致伸缩换能器的磁场在4个Galfenol棒之间形成闭合回路，漏磁较小，此磁路结构更适用于三维输出的换能器。

3 实验与分析

对双棒结构磁致伸缩换能器样机进行实验测试。测试系统包括换能器、电源箱、冷却循环系统和数据采集模块。冷却循环系统包括冷却机、质量流量计和冷却循环通道。电源箱为换能器提供直流偏置磁场和交流激励磁场。采用SQLAB II振动与噪声测试系统对换能器的振动加速度进行测量。图9为换能器在6 400 Hz、2 A驱动电流和5 A偏置电流工作条件下的实时加速度曲线。加速度曲线为正弦，波形较好，无杂波。平均加速度的幅值为2 000 m/s2。由此可知，所设计的磁路结构可以抑制换能器的漏磁，实现换能器在高频工作条件下有较大的输出特性。

对四棒结构磁致伸缩换能器样机进行实验。测试了当A棒和C棒工作时，换能器的输出轨迹，如图10所示。分析理论计算数据与实验数据，发现两者的运动变化趋势一致。计算的X方向和Y方向的最大位移均为25 μm。实验得到的X方向和Y方向的最大位移分别为22 μm和23 μm，略小于计算值。换能器输出轨迹的实验数据存在滞回特性，原因是在换能器的实际工作中存在不可避免的能量损耗。通过实验可知，所设计的磁路结构是有效的。换能器的输出轨迹与理论吻合。

4 結语

基于Maxwell方程组，对两台多棒结构磁致伸缩换能器样机进行了磁场分析，确定了最佳磁路结构。2台样机分别为应用于高频的双棒结构换能器样机和应用于微米级抛光的四棒结构换能器样机。研究发现，在6 000 Hz频率和2 A励磁电流下，驱动线圈串联的双棒结构换能器的平均磁通密度为0.879 T。与其他磁路结构相比，它的磁通密度更高且更均匀，适用于高频换能器。对四棒结构换能器进行了不同激励条件下的磁场分析，结果可知 A棒和C棒的磁通密度相位相差180°，B棒和D棒的磁通密度相位也相差180°， 磁通密度峰值均为0.45 T。4个Galfenol棒之间形成闭合回路，漏磁较小，具有三维位移输出，此磁路结构适用于微米级抛光的换能器。对2台换能器样机进行实验分析，可知根据磁场的仿真分析所设计的换能器满足设计要求。

参考文献：

[1]    王博文，曹淑瑛，黄文美. 磁致伸缩材料与器件[M]. 北京：冶金工业出版社，2008：176-179.

[2]    宣振兴，邬义杰，王慧忠，等. 超磁致伸缩材料发展动态与工程应用研究现状[J]. 轻工机械，2011，29（1）：116-119.

[3]    翁玲，王博文，孙英，等. 磁场和应力作用下的超磁致伸缩换能器的动态模型[J]. 电工技术学报，2008，23（12）：17-22.

[4]    LI Z，ZHANG X Y，GU G Y，et al. A comprehensive dynamic model for magnetostrictive actuators considering different input frequencies with mechanical loads[J]. IEEE Transactions on Industrial Informatics，2016，12（3）：980-990.

[5]    HUANG W M，LI Y F，WENG L，et al. Multi-field coupling model with dynamic losses for giant magnetostrictive transducer[J]. IEEE Transactions on Applied Superconductivity，2016，26（4）：1-5.

[6]    袁婭. 稀土超磁致伸缩换能器结构设计及性能优化[D]. 湘潭：湘潭大学，2013.

[7]    CHAKRABARTI S，DAPINO M J. Nonlinear finite element model for 3D Galfenol systems[J]. Smart Materials and Structures，2011，20（10）：105034.

[8]    李明范，项占琴，吕福在，等. 超磁致伸缩换能器磁路设计及优化[J]. 浙江大学学报（工学版），2006，40（2）：192-196.

[9]    陈爽，赵录冬，周杰，等. 稀土超磁致伸缩换能器磁路设计与仿真[J]. 机械设计与制造，2018（2）：43-46.

[10]  KARUNANIDHI S，SINGAPERUMAL M. Design，analysis and simulation of magnetostrictive actuator and its application to high dynamic servo valve[J]. Sensors and Actuators：A Physical，2010，157（2）：185-197.

[11]  王淑娟，康磊，李智超，等. 电磁超声换能器三维有限元分析及优化设计[J]. 中国电机工程学报，2009，29（30）：123-128.

[12]  陶孟仑，陈定方，卢全国，等. 超磁致伸缩材料动态涡流损耗模型及试验分析[J]. 机械工程学报，2012，48（13）：146-151.

[13]  EVANS P G，DAPINO M. Dynamic model for 3-D magnetostrictive transducers[J]. IEEE Transactions on Magnetics，2011，47（1）：221-230.

[14]  谭先涛，杨斌堂，孟光，等. 超磁致伸缩驱动器二维轴对称非线性驱动位移模型及有限元分析[J]. 天文研究与技术（国家天文台台刊），2010，7（4）：362-368.

[15]  鞠晓君，林明星，范文涛，等. 超磁致伸缩致动器结构分析及输出力特性研究[J]. 仪器仪表学报，2017，38（5）：1198-1206.

[16]  范进良，夏铁坚，刘强，等. 低频稀土换能器的磁路设计[C]// 中国声学学会青年学术会议，2005.

[17]  ZHU Y C，JI L. Theoretical and experimental investigations of the temperature and thermal deformation of a giant magnetostrictive actuator[J]. Sensors and Actuators A：Physical，2014，218：167-178.

[18]  GUO J，SUZUKI H，HIGUCHI T. Development of micro polishing system using a magnetostrictive vibrating polisher[J]. Precision Engineering，2013，37（1）：81-87.

[19]  王刚，徐颖，张传英. 一种三维微位移操作器[J]. 机械设计，2000，17（5）：35-37.

[20]  UENO T，SAITO C，IMAIZUMI N，et al. Miniature spherical motor using iron–gallium alloy （Galfenol）[J]. Sensors and Actuators A：Physical，2009，154（1）：92-96.

[责任编辑 田 丰]