实际问题与二次函数教学随笔

娄欣

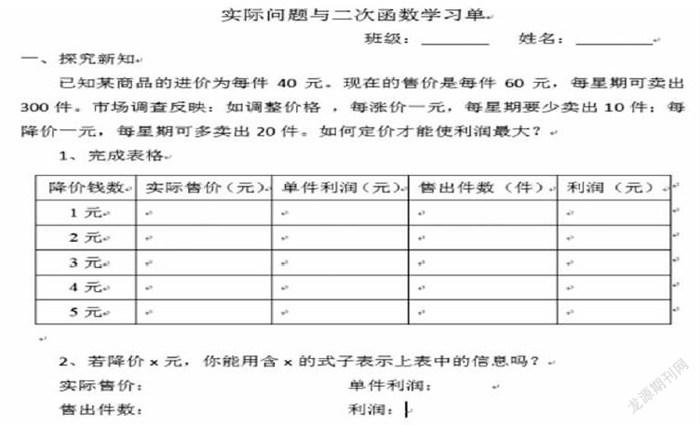
二次函数是初中数学的重点内容，也是难点内容，而且实际应用也是难点部分。在八年级时，学生学习一元二次方程与实际问题时，理解较困难，学习有难度，掌握不好。所以本次在备课时，我就思考，怎样做才能利于学生的理解呢？于是本次授课我采用的是用已知去代未知，让学生循序渐进的理解，课堂效果还不错。

上课之前，我知道二次函數应用是难点，何况该题目又是涨价又是降价。上课后我先让学生读题，并逐字分析，弄明白题意，最后让学生讨论并完成学习单上的前2个问题。

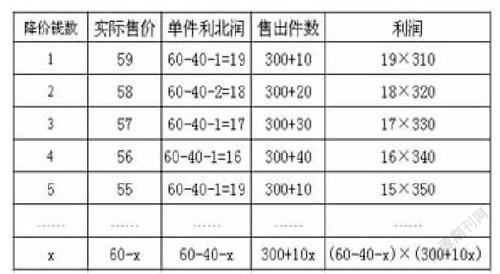
完成学习单后，由学生展示讲解。副板书采用列表的方式。分析过程如下：

教师：设获得利润为y元，商品定价为x元时，你能列出他们之间的函数关系式吗？

学生完成后，让学生观察这个式子有什么特点？（学生回答特点，发现是二次函数）。教师进一步提问这个二次函数有最大值或最小值吗？怎样求呢？这样就把实际问题转化为数学问题，求二次函数的最值问题。最后，由教师总结，求最大利润问题，设个未知的量，引导学生发现该题目中有两个变量——定价和利润，符合函数定义，从而想到用函数知识来解决——二次函数的最值问题，进而解决其他问题。这样学生比较容易理解。

初中阶段学生能够结合具体情境发现并提出数学问题建立数学模型，从不同角度寻求解决问题的方法，并能有效的解决问题，这是很重要的。

通过本节课的授课，让我体会到：授课的内容很难，但是教室应该在备课上多下功夫，多思考，怎样能把复杂问题简单化，怎样讲解才能易于学生理解呢？这也是我在以后的教学中要一直思考的。作为一名教师，我要努力备好课，上好课，育好人。