图模型在深度学习中的应用

来学伟

摘   要：简单介绍两种最为流行和有用的方法，针对每一种图模型进行了分析，详细介绍了如何使用一个图来描述概率分布的结构。最后判断哪些变量之间存在直接的相互作用关系，也就是对于给定的问题哪一种图结构是最适合的。

关键词：图模型;概率;因子

1    背景介绍

图模型在深度学习的研究领域应用非常广泛，研究人员曾提出过大量的训练算法、模型和推断算法。与普通的图模型研究者不同，基于深度学习的研究者们通常会使用完全不同的模型结构学习算法和推断过程。使用图来描述深度学习中的概率分布相互作用的方法也不止一種。首先，介绍几种最为流行和有用的方法。其次，分析如何使用一个图来描述概率分布的结构。最后，判断哪些变量之间存在直接的相互作用关系，也就是对于给定的问题哪一种图结构是最适合的。

2    常见的图模型

图模型可以被大致分为两类：基于模型的有向无环图和基于模型的无向模型。

2.1  有向模型

有一种结构化概率模型是有向图模型（Directed Graphical Model，DGM），也被称为信念网络（Belief Network）或者贝叶斯网络（Bayesian Network）（Pearl，1985）[1]。之所以命名为有向图模型是因为所有的边都是有方向的，即从一个结点指向另一个结点。这个方向可以通过画一个箭头来表示。箭头所指的方向表示了这个随机变量的概率分布依赖于其他变量[2]。画一个从结点a到结点b的箭头表示了用一个条件分布来定义b，而a是作为这个条件分布符号右边的一个变量。换句话说，b的概率分布依赖于a的取值。

假设Alice的完成时间为t0，Bob的完成时间为t1，Carol的完成时间为t2。t1的估计是依赖于t0的，t2的估计是依赖于t1的，但是仅仅间接地依赖于t0。正式地讲，变量x的有向概率模型是通过有向无环图G和一系列局部条件概率分布（Local Conditional Probability Distribution）p（xi|PaG（xi））来定义的[3]，其中PaG（xi）表示结点xi的所有父结点。x的概率分布可以表示为：

在之前所述的接力赛的例子中，这意味着概率分布可以被表示为：

这个结构化概率模型的实际例子能够检查这样建模的计算开销，能够验证相比于非结构化建模，结构化建模为什么有那么多优势。假设采用从第0 min到第10 min每6 s一块的方式离散化地表示时间，这使得t0、t1和t2都是一个有100个取值可能的离散变量。如果尝试用一个表来表示p（t0，t1，t2），那么需要存储999 999个值（t0的取值100×t1的取值100×t2的取值100减去1，所有的概率的和为1，所以其中有1个值的存储是多余的）。反之，如果用一个表来记录每一种条件的概率分布，那么记录t0的分布需要存储99个值，给定t0情况下t1的分布需要存储9 900个值，给定t1情况下t2的分布也需要存储9 900个值。加起来总共需要存储19 899个值。这意味着使用有向图模型需要存储的参数个数减少了50倍。通常意义上说，对每个变量都能取k个值的n个变量建模，基于建表的方法需要的复杂度是O（kn），就像之前讨论过的一样。现在假设用一个有向图模型来对这些变量建模。如果m代表图模型的单个条件概率分布中最大的变量数目（在条件符号的左右皆可），那么对这个有向模型建表的复杂度大致为O（km）。只要在设计模型时使其满足m<n，那么复杂度就会被极大减小。换一句话说，如果每个变量只有少量的父结点，那么这个分布就可以用较少的参数来表示。图结构上的一些限制条件，比如说要求这个图为一棵树，也可以保证一些操作（比如说求一小部分变量的边缘或者条件分布）更加高效。决定哪些信息需要被包含在图中而哪些不需要是很重要的。如果许多变量可以被假设为独立条件，那么这个图模型可以被大大简化。当然也存在其他简化图模型的假设。比如说，可以假设无论Alice的表现如何，Bob总是跑得一样快（实际上，Alice的表现很大概率会影响Bob的表现，这取决于Bob的性格，如果在之前的比赛中Alice跑得特别快，这有可能鼓励Bob更加努力，当然这也有可能使得Bob懒惰）。那么Alice对Bob的唯一影响就是在计算Bob的完成时间时需要加上Alice的时间。这个假设使得所需要的参数量从O（k2）降到了O（k）。然而，值得注意的是在这个假设下t0和t1仍然是直接相关的，因为t1表示的是Bob完成的时间，并不是他跑的时间。这也意味着图模型中会有一个从t0指向t1的箭头。“Bob的个人跑步时间相对于其他因素是独立的”这个假设无法在t0，t1，t2的图模型中被表示出来。只能将这个关系表示在条件分布中。这个条件分布不再是一个大小为k×（k−1）的分别对应着t0，t1的表格，而是一个包含了k−1个参数的略复杂的公式。有向图模型并不能对我们如何定义条件分布做出任何限制，它只能定义哪些变量之间存在着依赖性关系。

2.2  无向模型

有向图模型提供了一个描述结构化概率模型的语言。而另一种常见的语言则是无向模（Undirected Model），也叫作马尔可夫随机场（Markov Random Field，MRF）或者是马尔可夫网络（Markov Network）（Kindermann，1980）[4]。就像它们的名字所说的那样，无向模型中所有的边都是没有方向的。

有向模型适用于当存在一个很明显的理由来描述每一个箭头的时候。有向模型中，经常存在具有因果关系以及因果关系有明确方向的情况。接力赛就是一个这样的例子。之前运动员的表现影响了后面的运动员，而后面的运动员却不会影响前面的运动员。然而并不是所有情况的相互影响中都有一个明确方向关系。当相互的作用并没有本质的方向，或者是明确的有相互影响的时候，使用无向模型更加合适。作为一个这种情况的例子，假设希望对3个二值随机变量建模。使用无向模型，其中，随机变量对应着图中相互作用的结点。不像是有向模型中，在无向模型中的边是没有方向的，并不与一个条件分布相关联。

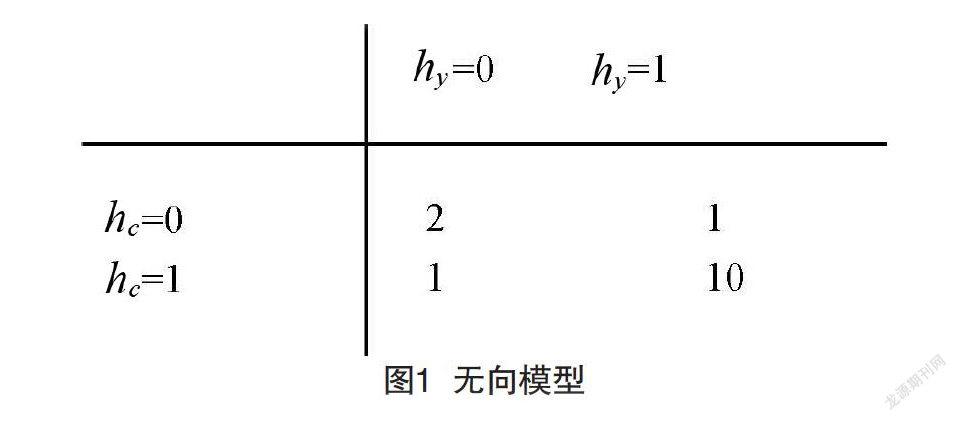
把对应你的健康的随机变量记为hy，对应你的室友健康状况的随机变量记为hr，你的同事健康的变量记为hc，如图1所示。

正式说，一个无向模型是一个定义在无向模型G上的一个结构化概率模型。对图中的每一个团（Clique）3C，一个因子（Factor）ϕ（C）[也叫作团势能（Clique Potential）]，衡量了团中变量的不同状态所对应的密切程度。这些因子都被限制为非负的。合在一起定义了未归一化概率函数（Unnormalized Probability Function）：

（3）

只要所有团中的结点数都不大，那么就能够高效地处理这些未归一化概率函数。它包含了这样的思想：越高密切度的状态有越大的概率。然而，不像贝叶斯网络，几乎不存在团定义的结构，所以不能保证把它们乘在一起能够得到一个有效的概率分布。

对于你来讲，你的室友和同事之间感冒传染的例子中包含了两个团。一个团包含了hy和hc个团的因子可以通过一个表来定义，可能取到下面的值：状态为1代表了健康的状态，相对的，状态为0则表示不好的健康状态（即被感冒传染）。你们两个通常都是健康的，所以对应的状态拥有最高的密切程度。两个人中只有一个人生病的密切程度是最低的，因为这是一个很少见的状态。两个人都生病的状态（通过一个人来传染给了另一个人）有一个稍高的密切程度，尽管仍然不及两个人都健康的密切程度。为了完整地定义这个模型，需要对包含hy和hr的团定义类似的因子。

3    结语

简单介绍两种最为流行和有用的方法。针对每一种图模型进行了分析，详细介绍了如何使用一个图来描述概率分布的结构。最后判断哪些变量之间存在直接的相互作用关系，也就是对于给定的问题哪一种图结构是最适合的。

[参考文献]

[1]刘   真.实用计算机图形与动画技術[M].北京：电子工业出版社，1998.

[2]渐渐遗忘的记忆.深度学习中结构化概率模型[EB/OL].（2019-05-24）[2019-09-15].https：//blog.csdn.net/h2026966427/article/details/90512114.

[3]袁   正.贝叶斯网络灵敏性分析方法及其在复杂系统故障诊断中的应用[D].合肥：合肥工业大学，2012.

[4]张   敏.基于SVM和CRF的病症实体抽取方法研究[D].成都：成都理工大学，2018.