Study on Expected Mature Age of Individual Ailanthus altissima

Bin CHANG Haifeng DONG Hongbo QIAO Dequan ZHANG3 Kehua WANG Shijiang LI

Abstract This study was conducted on the analytic tree and got the fitting empirical equation of tree growth, in which the tree growth rate was used as the variable and time as the independent variable. The arithmetical operation to the function got the mature age of tree growth, and the expected mature age of Ailanthus altissima was 21 a. In addition, the application as well as the research direction and matters needing attention were proposed.

Key words Ailanthus altissima; Expected mature age; Empirical equation; Analytic tree

In forestry production, the mature age of trees is the first problem to meet for the formulation of logging quota and the design of cutting areas, but there is little basic work on the forestry tables in Shandong, most of which is borrowed from other places or relevant national standards, and has not changed for decades. It will inevitably lead to large deviations. In this study, the mature age of Ailanthus altissima was studied by analyzing analytic wood data. A. altissima is the main tree species in four-side tree planting of Shandong Province. This tree species is beautiful in tree shape and fruit, and the fruit is matured in stages, forming a three-red multi-red landscape. Moreo6901028157643

ver, the tree species is tolerant to poor soil, resistant to pollution, and performs good in direct-seeding afforestation and natural regeneration. Therefore, exploring the growth law of A. altissima has a strong practical significance for promoting the construction of socialist ecological civilization. The mature age of A. altissima was explored in this study.

Source of Information

Due to limited fund, we carried out the study on the basis of previous survey materials. The analytic tree material was obtained from the average tree analytic tree of A. altissima that had normally grown for 9 years in the Majiahe Forest Farm, Guanxian County on April 3, 1984. The DBH was studied using the section of 0.6 m, and others using the 1 m section. Round disks were cut at the tree height of 5 cm (0 disk), 0.5, 1.3, 2.1, 3.1, 4.1, 5.1,  6.1, 7.1, 8.1 and 8.6 m, respectively. Interpretation was made strictly according to the technology for analytic tree, and relevant data were collected with 2 years as the age class (process omitted).

Research Methods

In order to save the cost, we carried out fitting test to various regression equations according to the research method introduced in references［1-3］, the research results of reference［4］and the research method and process of references［5-6］based on the analytic tree information, and finally used following mixed empirical equation to study the growth process of trees:

Y(t)=ea-b/t

Wherein a, b are the index parameters of the function to be solved, and e is the base of natural logarithm.

Tree growth is affected by a variety of factors, but those with the largest influence are the precipitation amount and the spatial and temporal distribution. In this study, we tried to use the empirical equation to fit the growth process of trees. The fitting equation of the maximum age of the ground diameter (including the equation from the derivation, which was stated in the research process) could get the mature age of ground diameter. The fitting equation of the maximum age of tree height could get the mature age of tree height. The same method was used to get the mature ages of DBH, DBH square, tree height and wood volume growth.

Research Process

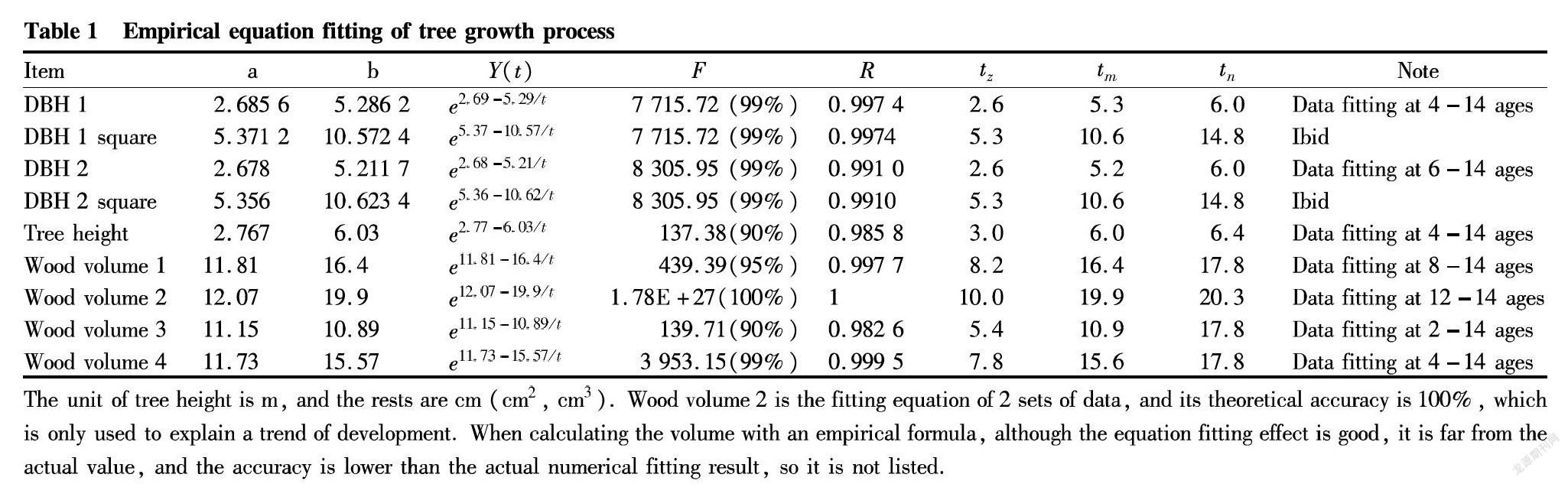
A linear equation was formed by taking the logarithm of the equation for tree growth process, and then, the unary linear regression was used to get the values of parameters a, b, which were tested by F test ad correlation coefficient R test. Passing the test means that the equation of tree growth is established. The calculation results were shown in Table 1. By looking up the table, the fitting results of wood volume 3 and tree height passed the F test with the reliability of over 90%, and wood volume 1 passed the F test with the reliability of over 95%, while others passed the F test and R test with the reliability of over 99% (100% for wood volume 2). The F test showed that the mathematical model (the empirical fitting equation) was applicable overall, and all items passed the correlation coefficient R test with the reliability of  99.9%, indicating that the relationship with the fitting equation was set up. Therefore, the item of DBH 1 was an example to illustrate the problems of using the fitting equation to solve the time for maximum current annual increment and quantitative maturity of trees. The extreme point of the equation for the DBH growth speed of the tree (current annual increment, which was completed through the derivation of the Y(t) function in the table, and the process was omitted with only the extreme point given, the same below) was  tz=2.6 a, which meant that the growth amount of the tree reached the peak at the second or third year, and there was only a single peak. The extreme point of the equation for the average growth speed of the tree (mean annual increment, which was completed through the derivation of the Y(t)/t function, and the and the process was omitted with only the extreme point given, the same below) was tm=5.3 a, indicating that the mature age of the tree was 5.3 a (only the DBH 1 fitting equation was given, and the fitting equation for other items were the same, thus omitted). In following discussion, the equations for growth fitting, tree growth speed and average growth speed of the tree were the same, and the meaning of tz and tm were also the same, so the calculation results were given directly. The mature ages of all the items are shown in Table 1. As shown in Table 1, compared the item square with the item, the values of the parameters increased by 1 time, and the accuracy was the same with the tested F values and R values, which was caused by the mathematical relations of the indexes. In order to compare with the cumulative fitting equation, we established the fitting equation of DBH square. In Table 1, the value of tn was the age at intersection point between the current annual increment and mean annual increment curves of the sample tree (the volume was obtained from the trend graph of the growth curve), which could serve as the mature age of the tree. Only the tm value of DBH square was far from the tn value, and the remaining tm values were very close to corresponding tn values. The tn value of DBH square was very close to the fitted value tm of the volume 4  equation, and the DBH square was very close to the tm value of volume 3. Therefore, empirical fitting equation was more suitable for wood volume, and the results were more reliable. As far as we are concerned, the maturity of a tree is the maturity of tree volume, so it would be more reliable to set the mature age of the tree in actual practice according to the results.

The unit of tree height is m, and the rests are cm (cm2, cm3). Wood volume 2 is the fitting equation of 2 sets of data, and its theoretical accuracy is 100%, which is only used to explain a trend of development. When calculating the volume with an empirical formula, although the equation fitting effect is good, it is far from the actual value, and the accuracy is lower than the actual numerical fitting result, so it is not listed.

When analyzing the test results by traditional methods, the mature age of A. altissima should be at about 10 years, but the conclusion was obtained through equation simulation under the conditions of lacking materials of 16 years and higher. Although in Table 1, the tm values differed greatly from the original standard (21 a) except the fitting equation of wood volume 2, the tm value and tn value of volume 2 were very close. However, since there were far too few data, the mature age of A. altissima was better set at 20 years.

Conclusions and Application

In order to conform to the national standard of the age class of 5 years, the mature age was set at 21 years, completely consistent with the original standard. The age group was divided as the following: young sampling forest of below 10 years, immature forest of 11-20 years, near-mature forest of 21-25 years, and over-mature of forest with the ages above 36 years.

Discussion

The original maturity standard of 21 a was made based on the standard of 5 years as the age class, and in this study, 2 years were used as the age class, so in order to make it convenient for production, the mature age was set at 21 a, which was more close to the reality. Under the conditions of lacking of the observation data of the age class of 16 years (and higher), growth curve and equation fitting were used to get the expected mature age. In this study, we carried out a coefficient simulation test and showed amazing correctness. This study was based on the age class of 2 years, and under the condition of few experimental data, the expression of the experimental target true value was basically satisfied, and the experimental results were ideal. Based on years of practical experience, it is found that A. altissima afforestation by direct seeding is better than seedling afforestation, and the growth rate of A. altissima is no less than that of all kinds of poplars. Furthermore, A. altissima has good quality, and is a more ideal furniture material. The sample tree in this study was in a forest grown from seedlings, and its growth was not very ideal, as its mean annual growth was only about 1/5 of that of fast-growing poplar. As for the research of forests grown by direct seedling, it is necessary to set up another study. This study showed high similarity and equation compatibility to previous studies on Quercus acutissima, Robinia pseudoacacia and conifers, so it was suggested that it could be applied in the production practice in future. Previously, due to the adjustment to the lack of data, the mature age of A. altissima always referred to similar tree species, and in this paper we tried to get the exact mature age of A. altissima using empirical equation. However, due to the lack of investigation data of higher age classes, the conclusion was not comprehensive. Interested colleagues can apply this method with the assistance of the new techniques and equipment of medical imaging technology that used in tree measurement, which may play a multiplier role, making this research more realistic. However, the application of empirical volume formula played an important role in making up for the shortage of experimental data. Limited by various conditions, all kinds of deviations can hardly be avoided, which can only be improved and developed in the research and production practice. However, the suggestions for forest production in this paper were only personal opinions, which required the approval and tests from the experts to put into application.

References

［1］KANG KJ. Forest measurement［M］. Beijing: China Forestry Publishing House, 1985. (in Chinese)

［2］CHEN HH. Mathematical statistics［M］. Beijing: China Forestry Publishing House, 1985. (in Chinese)

［3］LIU GJ. Review guide for vocational qualification test of registered consulting engineer (investment)［M］. Tianjin: Tianjin University Press, 2003. (in Chinese)

［4］GAO JH. Approach into desirable period of forest management in Shandong Province［J］. Journal of Forestry Engineering, 2003, 3: 6-8. (in Chinese)

［5］HU HY. Study on the actual maturity age of individual Pinus densiflora［J］. Journal of Shandong Forestry Science and Technology, 2010, 6: 36-37. (in Chinese)

［6］LI LP. Study on expected maturity age of Shandong Pinus densiflora［J］. Journal of Anhui Agricultural Sciences, 2017, 3: 184-186. (in Chinese)