基于自适应遗传算法Smith非线性PID的加热炉温度控制

张伟 李绍铭 闫成忍

摘要：由于工业加热炉的温度控制有很多不确定因素，导致系统呈现非线性并且加热炉温度控制有大滞后的缺点，很难做到对温度的精确控制。本文引入自适应遗传算法和Smith预估控制策略对加热炉的温度控制器进行改进，使得系统的调节时间缩短、滞后被抑制以及稳定性增强。实验结果表明：该方法能够有效地改进控制系统的超调、纯滞后的缺点;明显改善控制系统的动态性能和抗干扰能力，从而达到更好的控制效果。

关键词：温度控制;自适应;Smith控制器;抗干扰

中图分类号：TP273 文献标志码：A 文章编号：1008-4657（2019）05-0013-05

0 引言

轧钢加热炉控制器的作用是轧制过程为钢坯提供所需的温度，并控制加热炉内温度的恒定。加热炉温度控制的好坏是衡量控制系统特性的重要依据之一[1]。然而，实际工业生产过程中由于加热炉体积过大，内部温度存在分布不均匀，检测系统不能跟踪实时温度变化，导致无法建立精确的数学模型和有效的可控模型，并且工业生产中普遍采用的是PID控制算法，由于控制器的参数调整很麻烦，因而无法达到精确控制加热炉内温度[2]。针对加热炉温度控制的缺点。本文在传统工业PID控制算法的基础上，提出采用自适应遗传算法、Smith预估控制和非线性PID控制相结合的方法[3]，充分利用各种算法的控制优点对增益参数的全局寻优和对滞后的预估补偿。

1 非线性PID控制器模型

传统的PID控制器数学模型[4]

非线性PID调节器中增益参数和反馈的控制误差之间存在有函数关系。可以用函数关系式进行描述并在控制器的各个部分中发挥作用。所以控制能力比常规PID效果好。

2 控制器设计

2.1 自适应遗传算法整定

上式（3）～（5）中共有9个增益参数，这为参数调节带来很大难度，针对这个问题，本文引入自适应遗传算法，该算法具有多目标寻优、搜索高效等优点[7]，使用全局寻优的办法来确定各增益参数的值。在寻优过程中，只需设定合理的最优目标值对控制参数进行全局寻优[8]。若每次控制参数整定都应用该算法，那么被控对象将实现实时在线调整，缩短调节时间。控制系统框图如图1所示。

2.2 自适应函数设计

由于自适应遗传算法在寻优过程中把整个区间分解成无数各小区间，在每个小区间内进行参数寻优，当在某个区间内找到局部最优值，该算法有可能把这组值当成整个区间的最优值，最终很容易陷入局部最优[9]。因此适应度函数的设计要避免这个误区，既不能是寻优过程时间过长也要防止未成熟收敛现象[10]。由于控制决策的目标是要使输出期望值，并且要求调节速度快和超调量小，因此把反馈偏差e（t）、偏差变化率△e（t）和输出控制量u（t）作为非线性PID控制反馈环节三个重要的参数[11]，适应度函数的设计需要将其作为重要参数考虑进去，因此目标函数为

自适应遗传算法在非线性PID在增益参数确定和调整中有显著的优越性，用遗传算法对滞后问题的解决并没有起到预期效果，需要在控制原理上进一步的改进。Smith预估控制在滞后问题上具有一定的补偿能力，对系统的滞后补偿有很好的效果并可以增强系统的稳定性。

2.3 Smith预估控制器原理

Smith预估控制的作用主要应用于系统滞后部分，它在系统的反馈环节对系统进行预估补偿并保证系统的稳定性。在自适应遗传算法的非线性PID控制的反馈链路中引入一个预估补偿控制环节对滞后环节进行补偿，使控制效果明显提升。其控制结构原理图如图2所示。

通过在并联反馈环节引入一个预估补偿控制器，然后用常数分离的方法把滞后部分分离出作为单独的一项，按常规方法设计控制器G1（s）。一般G1（s）为PID控制的传递函数[13]。其等效的传递函数为

经过Smith预估补偿，滞后部分被分离出去作为单独的一项并且对系统带来的不稳定影响将明显减弱。

通過把Smith预估器并联到PID控制器的反馈环节，并把e-τs作为完整的一项分离出去，充分发挥Smith预估控制器的补偿作用，可有效提高系统的调节速度和抗干扰能力。因此整个控制系统结构框图如图3所示。

在任意给定t采样时刻，实际控制偏差是通过t时刻给定值r（t）和y（t）的差值得到

因此在非线性PID控制和自适应遗传算法控制的基础上，加入Smith预估控制可以对系统的滞后进行预估补偿并且不影响系统对加热炉温度的控制。

3 自适应遗传算法的Smith非线性PID控制在加热炉温度控制系统中的应用

产品质量的重要决定因素是加热炉内部的加热温度，但加热炉体积大、内部温度分布不均匀，导致在生产控制过程中出现非线性、时变性、滞后性，控制难度大，对应的数学模型也是在理想条件下建立起来的。传统的控制无法对炉内温度达到精确控制[9]。针对此加热炉建立数学模型，其传递函数为

式中，k的取值范围为[0.2，0.8]，T1的范围为[20，40]，T2的范围为[20，40]，τ的范围为[15，25]。对加热炉温度控制系统辨识，当k=0.5，T1=25，T2=35，τ=20时，随机输入（0，1）之间的任意数值，基于自适应遗传算法的非线性Smith PID控制器采集样本数为30，交叉概率和变异概率分别为：0.9、0.01;非线性PID控制器的参数kp1、kp2、kp3 的取值范围为[0，5]，kd1、kd2、kd3、kd4 的取值范围为[0，10]， ki1、ki2的取值范围为[0，5]。最优指标 J 各项参数设置为 z1=0.999，z2=0.001，z3=2.0，z4=100，通过建立数学模型非线性PID控制器的各项参数如表1所示。

通过仿真实验对本文的自适应遗传算法的Smith非线性PID 控制算法进行评价，仿真过程模拟PID控制、非线性Smith PID控制和自适应遗传算法的非线性Smith PID控制三种控制算法的控制速度、超调和稳定性并进行对比分析。仿真结果如图4所示。

图4是基于加热炉温度控制模型仿真的三条曲线分别为PID控制、Smith-PID控制和基于自适应遗传算法的Smith非线性PID控制仿真结果，从图中可以看出自适应遗传算法的Smith非线性PID控制达到预设目标的速度比PID控制和Smith-PID控制要慢，这是因为非线性PID增益参数的确需要采用自适应遗传算法的全局寻优方式，所需时间较长，而自适应遗传算法的Smith非线性PID控制回到理想状态的速度和超调量控制明显优于其他两种控制算法。

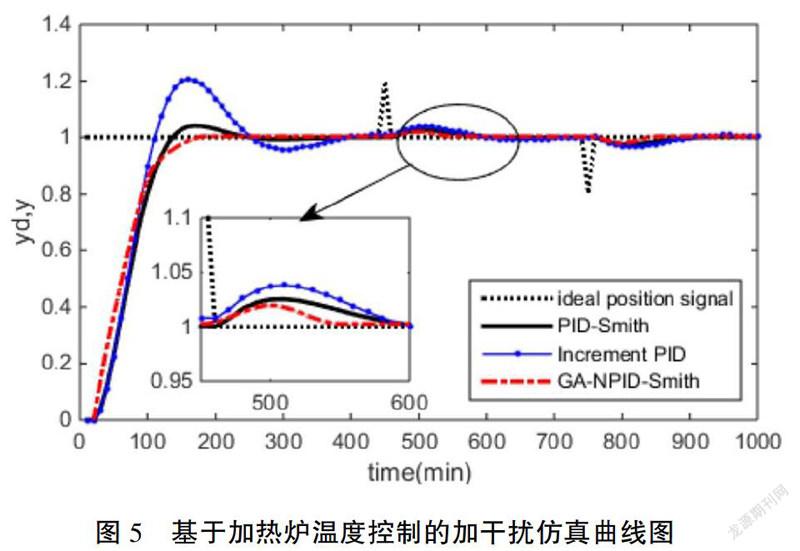
为了进一步验证自适应遗传算法的Smith非线性PID控制的稳定性和抗干扰能力，在三种控制方式下，随机对其加上扰动，仿真结果如图5所示。

由图5中仿真结果可以看出，加入干扰后，自适应遗传算法的Smith非线性PID控制的恢复能力要比其他两种方式所需时间少。在抗干扰能力方面，本文中自适应遗传算法的Smith 非线性PID控制有很好的抗干扰能力。

4 结论

本文将自适应遗传算法的Smith 非线性 PID控制应用于加热炉内温度控制系统，非线性PID的增益参数通过自适应遗传算法的全局寻优方式，找到最合适的增益参数，由Smith预估补偿控制针对加热炉温度控制滞后的特点进行预估补偿，最终使加热炉温度控制更加精确，在响应时间、超调量和振荡方面都有明显的改善，并且加热炉对外界的干扰恢复能力明显比其他两种控制方式快。因此针对加热炉温度控制使用更加优化的参数寻优算法和软件补偿方法可以起到很好的控制效果，在无法快速提高硬件响应速度时，通过优化算法能够使系统控制效果进一步提高。

参考文献：

[1]解英杰，尤洋，谢慕君.Smith-Fuzzy-PID在集中供热控制系统中的应用研究[J].计算机测量与控制，2014，22（9）：2 823-2 825.

[2]李阳.基于Smith-模糊PID的温度跟踪控制[D].武汉：华中科技大学，2017.

[3]高帅，杨少华，郭明安，等.基于遗传算法自整定和Smith预估的电子倍增电荷耦合器件温控系统设计[J].科学技术与工程，2016，16（29）：260-265.

[4]周颖，張磊，裘之亮，等.基于自适应遗传算法的非线性PID控制器[J].河北工业大学学报，2010，39（1）：47-50，55.

[5]韩华，罗安，杨勇.一种基于遗传算法的非线性PID控制器[J].控制与决策，2005（4）：448-450，454.

[6]程全，张凯.基于遗传算法的温度PID智能控制系统设计[J].沈阳工业大学学报，2018，40（4）：101-105.

[7]徐健义，杨遂军，许启跃，等.基于遗传算法的半导体制冷器非线性PID设计[J].测控技术，2017，36（6）：51-55.

[8]干树川，杨平先.基于模糊遗传算法的PID自整定研究[J].华北电力大学学报，2005（5）：45-48..

[9]吴廷强，阎昌国，罗德莲.基于积分分离模糊PID的温度控制系统设计[J].西南大学学报（自然科学版），2017，39（5）：185-189.

[10]Bouyedda Hocine，Samir Ladaci，Moussa Sedraoui，et al.Identification and Control Design for a Class of Non-minimum Phase Dead-time Systems Based on Fractional-order Smith Predictor and Genetic Algorithm Technique[J].International Journal of Dynamics and Control，2019，7（03）：914-925.

[11]高锦，章家岩，冯旭刚，等.基于失配补偿Smith-RBF神经网络的主蒸汽压力控制技术[J].重庆大学学报，2019，42（7）：105-113.

[12]Vidyadhar H Iyer，Mahesh S，Rohit Malpani，et al.Adaptive Range Genetic Algorithm：A hybrid Optimization Approach and Its Application in the Design and Economic Optimization of Shell-and-tube Heat Exchanger[J].Engineering Applications of Artificial Intelligence，2019，85：444-461.

[责任编辑：郑笔耕]