浅谈中学媒体素养在初中数学课程中的整合

梁荣崧

【摘要】  近年来，有关中学媒体素养的培养问题呼声越来越高，但是现在初中数学课堂教学中教学目标不合理、提问频繁且效果不佳、课堂教学依然以教师为中心、学生参与度比较低、教师处理教材不恰当等现象。对于此现象，可通过媒体素养强化课堂教学环节、培养教师进行教学反思的能力等方法，以提高课堂教学的质量。

【关键词】  中学媒体素养 初中数学 课堂教学 动点综合

【中图分类号】  G633.6             【文獻标识码】  A   【文章编号】  1992-7711（2019）06-090-02

一、初中数学课堂教学枯燥、乏味

现在很多老师的课堂上，依然受应试教育的影响，教师讲授的内容都是依照考试大纲的要求进行，“中考考什么，我们就教什么”，老师的知识水平和阅历肯定是比学生要高很多，老师往往不能体会学生在接受新知时的困难，套路非常死板、生硬，学生听课感到很枯燥，从而效果就会变得愈发低效。

要想取得较好的教学效果，我认为可采取以下方法解决：在实施探究式学习时，老师需要把新知降低“姿态”，将新知识融入生活，使学生感受到数学与我们的平常的生活息息相关，并且紧紧地服务于生活，并从中享受学习数学带来的乐趣。

我们看课堂实录：七年级数学上册《有理数的加法》

老师：“（-6）+（+5）=？能不能根据自己的生活经验探索结果？”

学生1：（-6）+（+5）=-1.例如：在教室里，将向教坛黑板方向走记为正，将向学习园地走记为负。向学习园地走6米，记作-6，又向教坛黑板方向走5米，记作+5米。整个过程往学习园地走了1米，记作-1.因此，（-6）+（+5）=-1.

学生2：我向同学借了6本作业簿，记作-6，书包里还有5本作业簿，记作+5.我将5本作业簿还给同学后，还欠1本作业簿，记作-1.所以，（-6）+（+5）=-1.

老师：这两位同学联系了我们生活中的实际例子，探索出（-6）+（+5）=-1.那么，同学们是不是也可以借助这两位同学探索出方法来解决其它有理数的加法运算。

这样联系到学生平时学习、生活中常见实例的探索设计，不仅学生有兴趣，也能让学生感受到数学来源于生活又服务于生活，还能更加学生有自信心，这样就会让学生爱上数学课堂，从而提高数学成绩。

二、初中数学课堂教学提问过于频繁、流于形式

笔者听了九年级数学一节总复习公开课，授课老师在40分钟的课堂上提问的次数达到了32次，这些问题中多次出现“是不是这样做？”“这样的做法对不对？”“你们会做了吗？”“这样的解法是不是很好呀？”等等这些没有任何可以激发学生思维的问题，都是比较封闭的提问，这样教授下去的话，学生得不到很好的发展。

为了能更好地解决这样死板的教学，我认为课堂上应该积极调动学生学习的主动性，让学生有足够的时间去思考问题，让学生真正地动起笔来，可以写出解题的过程，也可以写出解题的思路、方向，充分发挥学生的思维能力，让学生大方地讲解题目，充分地参与到课堂中来，成为课堂的主人，学生自己能从课堂上获得自信，从而喜欢上数学课，才能学到更多的知识。例如，在讲授《圆》的复习课时，我以下面的一道中考题（改编）作为例题，进行授课。

例1  如图，在△ABC中，∠B=90°，OA=OC，过O作OD⊥AB于点D.延长DO交⊙O于点E，∠OFE=90°.连接DF并延长交直线BC于点G，连接EG。

（1）求证：FC=GC.

（2）求证：EG是⊙O的切线。

（3）若EG=6，CG=2，求BC的长。

评析：这是2014年广东省中考数学试卷改编的几何压轴题。它以人教版教材九年级上册102页的一个习题（习题24.2中第12题）为母本改编的中考压轴题。考查的知识点覆盖面比较大，（1）问求证两条线段相等，考查学生的基础知识;（2）问是常见的考点，求证圆的切线问题;（3）问是给出线段的长度，求另外一条线段的长度。这三小问紧紧依照考试大纲里对圆这一章内容的要求，具备很好的区分度。所以，我们老师在课堂上要合理利用好时间，让学生有时间对这样的题目进行思考，让不同层次的学生都能对这类型的题目进行解答。

中考的题目来自课本的例题、习题，然后在这些题目的基础上加以改编，难度稍微大于例题、习题。因此，我们在平时的教学过程中，要重视课本的练习题，认真讲解，并发挥我们教师的能力，做出适当的变式教学，举一反三，让学生能够做到做一题会一类。

通过上面选取的典型例题，让学生清楚地了解到中考对《圆》的内容的考试要求，同时也较好地引导学生思考问题、分析问题，写出解题过程、思路，让学生说出解题思路，说出一题的多种解法，分析各种解法的好的地方，取长补短，学生可以在课堂上获得巨大的满足感、自信心，很有收获。

三、初中数学课堂教学讲授内容简单且反反复复

笔者参加阳江市中小学教师信息技术应用能力提升工程校本研修活动，在某校听了一节九年级数学总复习《动点综合问题》，该教师在课堂上讲授的全都是非常基本的动点平移题目，条件几乎一成不变，结论也大都相同。该老师讲解如下：

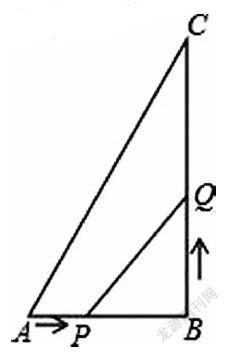
例2  如图，在Rt△ABC中，∠B=90°，AB=12cm，BC=24cm.点P在边AB上以1cm/s的速度从点A向点B运动，点Q在边BC上以2cm/s的速度从点B向点C运动，若点P、Q分别从A、B同时出发，设运动时间为t（s）。

（1）当t=3时，求S△BPQ.

（2）试写出四边形ACQP的面积S（cm2）与t（s）之间的关系式。

（3）当四边形ACQP的面积S最小时，求出此时t的值，并求最小面积。

整节课下来，授课老师都是围绕着这样的图形不停地进行提问，“AP的长度是多少？”“PB的长度是多少？”“BQ的长度是多少？”“CQ的长度是多少？”“如何表示△PBQ的面积呢？”这样的提问过于频繁、啰嗦，且效率低下，学生听着也会感到无比厌烦，做题的热情逐渐降低。该老师用了15分钟讲解完这道题目后，又给出了如下这道题目：

例3  如图，在△ABC中，AC=4cm，BC=3cm，∠C=90°.点E在边BC上以1cm/s的速度从点B到点C运动;同时，点F在线段AC上以2cm/s的速度从点C到点A运动.当某一点到达终点后，E、F两点均停止，设运动时间为t（s）。

（1）求△CEF的面积 S（cm2）与 t（s）之间的关系式;

（2）若S△CEF =2cm2，求此时t的值。

（3）△CEF的面积是否存在最大值？若存在，请求出此时t的值，并求出这个最大值。若不存在，请说明理由。

实际上，这两道例题所表述的内容几乎是一样的，涉及到的动点问题和考点也是类似，对提高学生的综合解题能力起不到很好的效果，学生在这样的课堂上，只会感到很乏味，甚至无聊。

四、要将中学媒体素养融入到数学课程中，并加以整合

笔者认为，要想在这样的课堂上再加以修饰，对题目进行合理的变式，提出的问题层层递进，学生就会有一种眼前一亮的感觉，学习兴趣顿然而生，就会更加积极地思考老师提出的问题了，学生自己动手完成这样的动点综合题后，具有满满的幸福感。我认为应充分利用好媒体素养教学，增加以下例题加以拓展：

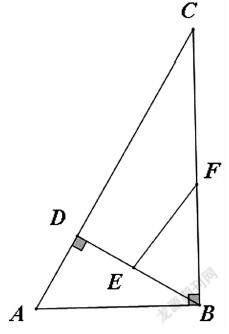
例4  如图，在Rt△ABC中，BC=16cm，AB=12cm，∠BDC=∠ABC=90°.点P在线段BD上以1cm/s的速度由点D向点B运动;点F以相同的速度，在线段BC上由点B向点C运动，两点同时出发，当点E运动到B时，两点都停止。设运动时间为t秒。

（1）求線段BD的长。

（2）当△BEF与△ABC相似时，求t的值。

（3）是否存在t的值，使得△BEF是等腰三角形？若存在，求出t的值;不存在，请说明理由。

此考题的区分度比较明确，第（1）问考查了用t的式子去表示线段的长度，学生基本上都能做出来，确保学生能够拿到分数;第（2）问先用t的式子表示出线段的长度，同时也考查了分类讨论思想，对学生的思维提出了更高的要求;第（3）问既考查了分类思想，也考查了方程思想，也可以利用等角的三角函数值相等的性质，从而用锐角三角函数的知识解答之，方法多种多样，为学生从不同角度去思考问题、解答问题提供了很好的方向。把学生的学习兴趣提上来之后，趁着学生带着渴望的热情去表现自己的时候，我会趁热打铁，让学生吃的好，吃的饱。

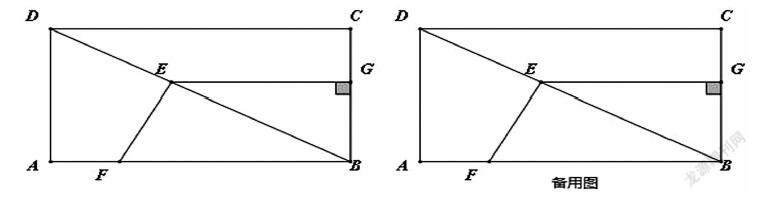
例5  如图，在长为8cm，宽为6cm的长方形ABCD中。点E在对角线BD上以2cm/s的速度从点B向点D运动;同时，点F以相同的速度，在边AB上从点A向点B运动.EG与CD保持平行，设运动时间为t（s）（0

（1）当t为何值时，点F在线段BD的中垂线上。

（2）求出四边形BGEF的面积为S（cm2）与时间t的表达式。

（3）是否存在S四边形BGEF：S长方形ABCD=9：50？若存在，求出t的值;若不存在，说明理由。

这样有深度，考点覆盖面广，综合性强，每一小题难易程度明显的题目，通过点、线、面的运动，把函数、常见的几何图形融合在题目中，学生认真思考后，多动手，做到把分拿足，掌握得会比较快，思维能力得到进一步的提升，成绩也会很快提高上来。

要想从40分钟的课堂上取得好的教学效果，除了笔者以上提到的几点对策外，教师在课后还要进行有效的反思，认真反思一下课堂上讲授的内容是否能让学生消化的好、反思提出的问题是否恰当、反思学生是否积极参与到课堂中来、反思讲解的题目是否精确。只有通过不断地反思教学，才能让我们的课堂更有效率，学生听课就会更加认真，学生学习兴趣也会更加浓厚，为取得好的成绩做好了铺垫。

[ 参  考  文  献 ]

[1]郭法奇.如何从应试教育走向素质教育.河北师范大学学报，2013.

[2]赵迪.让数学贴近生活让生活步入数学课堂。中华少年：研究青少年教育，2013.

[3]岑柏松.提问有“度”——谈初中数学课堂教学提问的技巧.语数外学习，2013.