巧用规律 化繁为简

赛先生

德国数学家高斯被誉为“数学王子”。他推动了多个数学领域的发展，这得益于他从小养成的爱思考、爱总结、爱找规律的习惯。

据说高斯在读小学时，有一次老师出了一道数学题：1+2+3+……+99+100=？没过多久，高斯就说算好了，答案是5050。老师惊讶得张大嘴巴，答案是正确的，高斯怎么算得如此迅速？

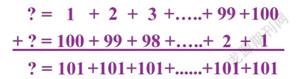
高斯告诉大家，他将“1+2+3+……+99+100”写成一排，再在下面写“100+99+98+……+2+1”，每列上下两数相加等于101，共有100个101相加，100×101=10100。那么，1+2+3+……+99+100=10100÷2=5050。

用高斯的方法，我们可以推导出求正整数依次相加之和的公式吗？1+2+3+……+（n一1）+n=？

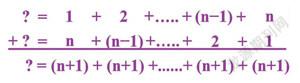
同样的，我们把“1+2+……+（n一1）+n”写成一排，在下面对应写“n+（n一1）+……+2+1”，每列上下两数相加等于n+1，共有n个n+l。那么，1+2+3+……+（n-1）+n=（n-1）+n/2。

我们如果将“1+2+3+……+（n-1）+n”具体化为如下图的石子堆，能发现什么？

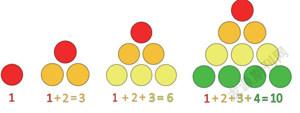
1粒石子、1+2粒石子、1+2+3粒石子、1+2+3+4粒石子……我们观察后不难发现，每堆石子都可以被排成等边三角形。石子总数分别为1、3、6、10……这些数被称为三角形数。也就是说，正整数依次相加的和（n-1）+n/2必是三角形数。

我们继续探索，稍微改变那4堆石子的排法，让它们排成等边直角三角形。

然后，如上图所示，我们用两个相同的等边直角三角形石子堆构成长方形石子堆。通过观察，我们发现，长方形石子堆一边是n、另一边是n+1，共有石子数为n（n+1）。

我们来检验这一结论：三角形石子堆的石子数为（n+1）n/2，两个三角形石子堆的石子数是2x（n+1）n/2=n（n+1），与刚刚算的结果相同。

我们在生活中会遇到三角形数吗？当然会！比如堆木桩，如果人们在地上平放45个木桩，再依次往上放木桩，把木桩堆成等边三角形，一共能堆多少个木桩？我们很快就可以算出答案45x（45+1）/2 =1035。

举一反三，对很多问题，我们可以快速解答。假設有7位来自不同学校的学生参加一个会议，在参会前俩俩握手认识，他们一共握手多少次？

我们来分析一下，第1位学生与其他6位学生分别握手，握手6次。第2位学生已经与第一位学生握过手了，只需与其余5位学生握手5次。第3位学生已经与前两位学生握过手了，只需与其余4位学生握手4次。如此类推，第4位学生接下来握手3次，第5位学生接下来握手2次，第6位学生接下来握手1次，第7位学生不用再握手了。

看，上图和我们之前看到的等边三角形石子堆如出一辙，那我们很快就能算出来：6x（6+1）/2=217位学生一共握手21次。

如果宴会上12位朋友俩俩碰杯，共碰杯多少次？同理，我们也可以这样求解：11x（11+1）=66，12位朋友一共碰杯66次。

这样的例子有很多。数学与生活紧密联系，还有很多规律等待人类学习、发现，我们继续探索吧！