三栖四旋翼模型与PID控制设计研究

张鹏 何振鹏 张永浩 张志远 迟炳哲

摘 要：本文在三栖四旋翼机体结构和飞行原理的基础上，利用牛顿-欧拉法对无人机进行动力学受力分析，建立相应数学模型，通过四旋翼无人机的数学模型分析，设计了比例-积分-微分（PID）控制器，利用MATLAB进行仿真验证。

关键词：三栖四旋翼;建模;PID;Simulink

中图分类号：V249.1 文献标识码：A 文章编号：1003-5168（2019）07-0083-03

Abstract： Based on the structure and flight principle of the triphibious quadruple-rotor airframe， the dynamic force analysis of the UAV was carried out by Newton-Euler method， and the corresponding mathematical model was established. Through the analysis of the mathematical model of the quadruple-rotor UAV， the proportional-integral-differential （PID） controller was designed and verified by simulation with MATLAB.

Keywords： three-habitat four- rotor uav; modeling; PID; Simulink

建立精确的无人机模型对控制算法的实际应用具有重大意义。本文把包括机体、电机以及螺旋桨在内的所有硬件都看成刚体系统，在SolidWorks软件中建立X型四旋翼无人机实体模型，从中获得惯性参数。从动力学原理出发，建立较为全面的无人机数学模型，并设计PID控制系统，实现对四旋翼无人机位置、姿态控制。

1 机体结构动力模型与飞行原理

机体结构动力模型拥有3种不同的运动形式，能够实现水陆空三栖运动，其模型图如图1所示，主要的动力元件来源于4个旋翼。该模型由于要适应水中的运动，所以将四旋翼的主体部分改成船体造型，但是由于增加了翼臂、电机、旋翼这些结构之后，使整体结构重心上移，导致其在水中运动时受力很难达到平衡。因此，该模型在主体部分两侧增加了平衡舱体，使无人机在水中或在陆面运动时能够维持平衡。为减轻机体重量，舱体材料用泡沫塑料，在每个舱体前后各加了一个橡胶轮（减少在地面降落时产生的冲击和在地面运动时受的变载），以便在陆上行驶。

1.1 空中飞行

无人机拥有4个旋翼且具有对称性，其结构简图如图2所示。飞行器控制机体的实时姿态和位置通过4个电机转速和1个舵机转角来实现的，电机转速的改变会改变每个旋翼的升力，而舵机转角改则决定了电机3、4在X轴方向上的投影牵引力[Fa3]和[Fa4]的大小以及两电机在各自位置上产生升力的大小。

无人机拥有5种不同的飞行方式：垂直运动、偏航运动、俯仰运动、横滚运动以及前后运动。相对于传统四旋翼无人机，本设计的亮点在于优化了无人机的前后运动。

传统的四旋翼无人机实现前后运动是通过改变4个电机转速，使飞行器发生一定程度的倾斜，从而使旋翼拉力产生水平分量实现无人机的前后运动。这对无人机的稳定性会产生很大影响，且对于其使用也会产生很大的局限性。对于优化后的无人机来说，要实现前后运动则不需要使机体发生倾斜，如图2、图3所示，在舵机驱动下使3、4电机向X轴方向倾斜，从而使3、4电机上的旋翼产生水平拉力，实现无人机的前后运动，在此过程中保证了机体稳定性。

1.2 水中运动

四旋翼无人机在水中运动时由机体下方的两个仓体（舱体下面是塑料泡沫，可以有效减轻机体重量）在水中产生的浮力来平衡船体重力，使无人机在水中Z轴方向达到平衡。通过设计使此时无人机的重心位于液面下，这样避免了无人机在前后运动或偏转过程中发生倾覆的可能。在水中运动时的动力来源于4个旋翼，运动原理与空中飞行相同。

1.3 陆面行驶

四旋翼无人机在每个舱体下方的前后位置都装有2个橡胶轮，保证无人机在陆面上平稳行驶。其动力来源于4个旋翼，运动原理与空中飞行相同。

2 建立数学模型

2.1 模型说明

针对四旋翼无人机，本文做如下假设和说明。本研究所用的导航坐标系（用N表示）是地理坐标系，原点选在无人机所在位置;Z轴沿当地椭球的法线指向天空;X轴在当地水平面内沿着当地经纬度线指向东;Y轴沿着当地子午线方向指向北，满足右手定则。无人机机体坐标系用B表示，将无人机的质心作为机体坐标系的原点;X轴沿质心指向1、2电机质心连线的几何中心;Y轴沿质心指向2、3电机质心连线的几何中心，满足右手定则。

为准确的确定四旋翼无人机的姿态，欧拉角定义如下：①俯仰角[θ]：B系与N系在OX轴方向的夹角;②横滚角[φ]：B系与N系在OY轴方向的夹角;③偏航角[Ψ]：B系与N系在OX轴以及N系在OXY平面上的投影夹角。

2.2 无人机的受力分析

空气阻力：[f=γtvb]，[γt]为平动空气阻力系数，方向和v的方向相反。

空气阻力矩：[τ=γrΩb]，[γr]是转动空气阻力系数，方向和[Ωb]的方向相反。

螺旋桨推力：[Ftj=kw2j]，j=1，2，3，4;k是螺旋桨升力系数，方向指向Z轴正方向。

螺旋槳阻力矩：[Ftj=αw2j]，j=1，2，3，4;[α]是螺旋桨阻力系数，方向和螺旋桨角速度方向相异。

重力：Mg方向指向Z轴负方向。

2.3 四旋翼无人机的数学模型

有牛顿第二定理得到平动方程：

[xyz=RM00j=14kw2j-1MRγtRTv i-000]         （1）

式中：[RTv i]表示B系下的速度;[γtRTv i]表示B系下的平动空气阻力大小;[RγtRTv i]表示N系下的平动空气阻力大小。

由角动量定理及哥氏定理得转动方程：

[Ωb=-j=14I-1ΩbIcrWbj+I-1IcrWBJ-I-1ΩbIΩb+I-1Mb+δM]           （2）

合外力矩：

[Mb=-γr0  -r  qr    0   -p-q   p   0+0.5ak-w21+w22+w23-w240.5ak-w21-w22+w23+w24αw21-w22+w23-w24]（3）

电机角速度矢量：

[Wb1=0  0  -W1;Wb2=0  0  -W2;Wb3=0  0  -W3;Wb4=0  0  -W4]       （4）

2.4 模型参数

通过在SolidWorks建立无人机模型，通过SolidWorks软件计算得到无人机质量、惯性参数，其他参数参考文献[1-5]取合理质，如表1所示。

3 串联模糊PID控制器设计

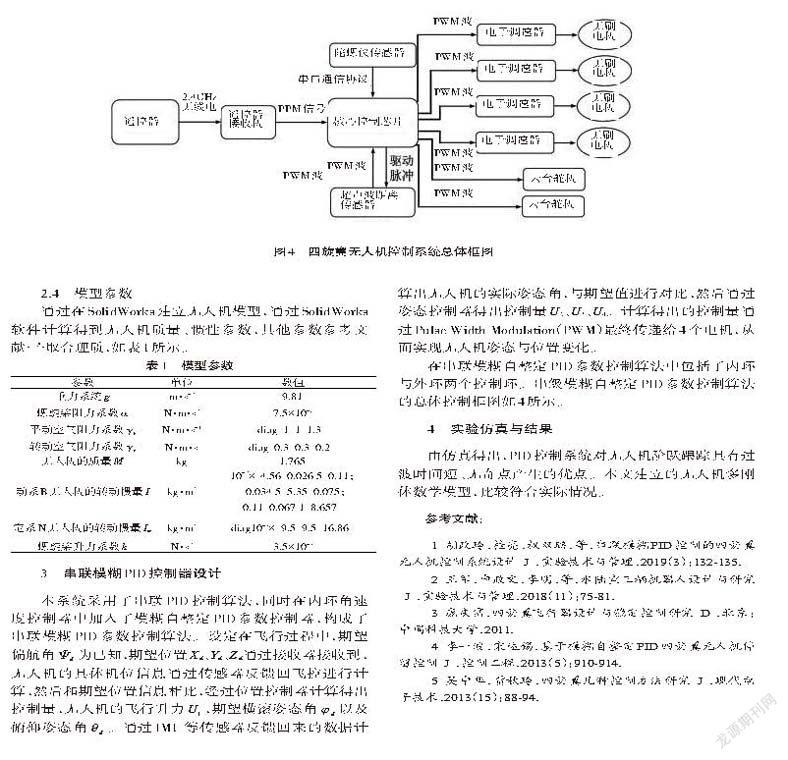
本系统采用了串联PID控制算法，同时在内环角速度控制器中加入了模糊自整定PID参数控制器，构成了串联模糊PID参数控制算法。设定在飞行过程中，期望偏航角[Ψd]为已知，期望位置Xd、Yd、Zd通过接收器接收到，无人机的具体机位信息通过传感器反馈回飞控进行计算，然后和期望位置信息相比，经过位置控制器计算得出控制量，无人机的飞行升力[U1]，期望横滚姿态角[φd]以及俯仰姿态角[θd]。通过IMU等传感器反馈回来的数据计算出无人机的实际姿态角，与期望值进行对比，然后通过姿态控制器得出控制量U2、U3、U4。计算得出的控制量通过Pulse Width Modulation（PWM）最终传递给4个电机，从而实现无人机姿态与位置变化。

在串联模糊自整定PID参数控制算法中包括了内环与外环两个控制环。串级模糊自整定PID参数控制算法的总体控制框图如4所示。

4 实验仿真与结果

由仿真得出，PID控制系统对无人机阶跃跟踪具有过渡时间短、无奇点产生的优点。本文建立的无人机多刚体数学模型，比较符合实际情况。

参考文献：

[1]胡改玲，桂亮，權双璐，等.串联模糊PID控制的四旋翼无人机控制系统设计[J].实验技术与管理，2019（3）：132-135.

[2]王军，申政文，李明，等.水陆空三栖机器人设计与研究[J].实验技术与管理，2018（11）：75-81.

[3]庞庆霈.四旋翼飞行器设计与稳定控制研究[D].北京：中国科技大学，2011.

[4]李一波，宋述锡.基于模糊自整定PID四旋翼无人机停留控制[J].控制工程，2013（5）：910-914.

[5]吴中华，贾秋玲.四旋翼几种控制方法研究[J].现代电子技术，2013（15）：88-94.