基于修正灰狼算法的水火电系统优化调度研究

裴丁彦 李雨 邹珊 陈金凤 蒋正清

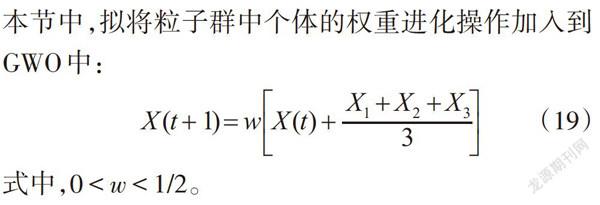
摘要：水火电短期调度一直是电力系统中的经典研究课题之一。对含有火电机组组合的水火电系统短期优化调度问题开展研究。对调度问题进行数学建模，明确模型目标函数以及发电系统内各式的约束条件。针对灰狼算法不足，引入混沌初始化、小生境技术以及混合粒子群技术对标准灰狼算法进行修正处理。利用修正后的灰狼算法对仿真实例进行求解。4种不同算法计算结果表明，BGWO-MGWO算法计算的平均费用相较BPSO-PSO、BGSA-GSA、BCWO-GWO分别降低了26.2‰、13.4‰、6‰，说明修正后的算法能够有效解决特定调度问题。

关键词：水火电联合调度;灰狼算法;混沌初始化;小生境技术;混合粒子群技术

中图法分类号：TM734

文献标志码：A

DOI：10. 15974/j .cnki.slsdkb.2019.08.016

1 研究背景

能源问题作为目前全世界面临的最大问题之一，是全球关注的热点。对于我国而言，能源问题主要体现在能源利用程度不够，资源浪费以及人均占有量少等方面。据中国科学网发布的全国电力总装机容量数据，我国能源结构还是以火力发电为主，总装机容量10.5亿kW，占63.98%;水力发电次之，总装机容量3.3亿kW，占20.02%[1];风电装机容量1.5亿kW，占9%;太阳能装机容量7 742万kW、核电3 364万kW，总共占7%。由于我国的火电站以煤燃烧为主要生产方式，导致近年我国煤炭消耗大幅增加，引发环境污染以及气候变化等问题。因此解决我国能源问题的办法应为大力开發可再生清洁能源和节能减排提高能源的利用率[2]。水电能源作为我国除火电能源外最大的可再生能源，以其发电成本低廉、机组启停机迅速、对环境污染小且可再生等优势，越来越受到人们的重视。

传统的数学规划方法如动态规划[3]以严格的数学理论支撑，在解决水火电调度问题时，能够保证算法求得全局最优解。但在求解大规模复杂问题时会出现维数灾而导致寻找不到最优解。智能优化算法如粒子群算法（PSO）[4-5]、引力搜索算法（ GSA） [6-7]、差分进化算法（DE）[8-9]、模拟退火算法[10]是近几十年来兴起的一种求解复杂数学问题的方法。智能优化算法在解决大型且复杂的非凸问题时，不受约束条件和目标函数形式的限制，能在较短的时间内计算出可行解。因此，智能算法在水火电联合调度问题上得到了广泛关注和应用。

2 水火电优化调度模型构建

2.1 模型目标函数

水火电优化调度模型目标函数为

3 灰狼算法及其修正策略

3.1 灰狼算法

灰狼算法（GWO）是Mirjalili等人于2014年提出来的一种基于种群的随机优化算法。灰狼算法的数学模型主要从狼群的等级制度、追踪、包围、攻击猎物中构造。具体计算步骤详见文献[11]。为解决离散型数学问题，E.Emary等于2016年提出了二进制灰狼算法（BGWO）[12]。BGWO算法与标准GWO算法相比，粒子的位置只有O或1两种状态，粒子位置的更新由每次迭代得到的种群最优的前3个个体信息决定。

3.2 灰狼算法的修正

标准灰狼算法在求解实际应用问题时往往需要进行一些适当的修正。本文采用3种修正策略使修正后的灰狼算法能获得更好的求解效果。

（1）混沌初始化。大多数智能算法都是由每一代种群中最好的个体来引导下一代种群的迭代计算，那么由初始化得到的第一代种群对最后搜索到的最优解有着相当大的影响。当初始化产生的种群中有一个粒子恰好出现在最优解附近，那么算法必将能更快、更好的搜索到最优解。因此，人们便寻找一些有效的初始化手段，以提高算法的搜索结果。

混沌序列就是一种比较有效的初始化手段。它能按一定的规律不重复的遍历所有状态，从而提高算法的全局搜索能力。本文采用Tent混沌序列来产生初始种群。因为Tent映射有着严格的数学理论支撑，具有可靠性，并且实验表明Tent映射遍历均匀性良好。Tent映射经贝努利位移变换，具体数学表达式如下：

应用Tent映射初始化种群步骤详见文献[12]。

（2）小生境技术。将小生境技术融合到灰狼优化算法中。通过种群中个体之间的距离来划分粒子相似程度的大小，从而将整个种群划分为许多小的种群，在小的种群中繁衍出下一代个体。利用个体之间的距离来划分灰狼种群，通过罚函数对适应值较差的个体进行处理，从而达到寻优的目的。

（3）混合粒子群技术。GWO算法在搜索过程中，个体的前进方向是由其他优秀个体的合力计算所得到的。在更新位置过程中，只有其他个体当前位置发挥作用，而没有个体位置记忆功能。因此在本节中，拟将粒子群中个体的权重进化操作加入到GWO中：

4 仿真计算

本文以含有10个火电机组及4个梯级相连水电站的水火电系统作为测试系统，来验证BGWO-MGWO算法对于解决水火电系统短期调度的有效性。设定种群个数为30个，最大迭代次数为200次，小生境半径设置为0.5，惩罚比例设置为1.1，个体权重设置为0.5，调度周期为24 h。各个水电站的流量约束、水库库容约束、水电站出力以及水电站连接方式等数据取自文献[13]，各个火电机组的参数信息来自文献[14]。

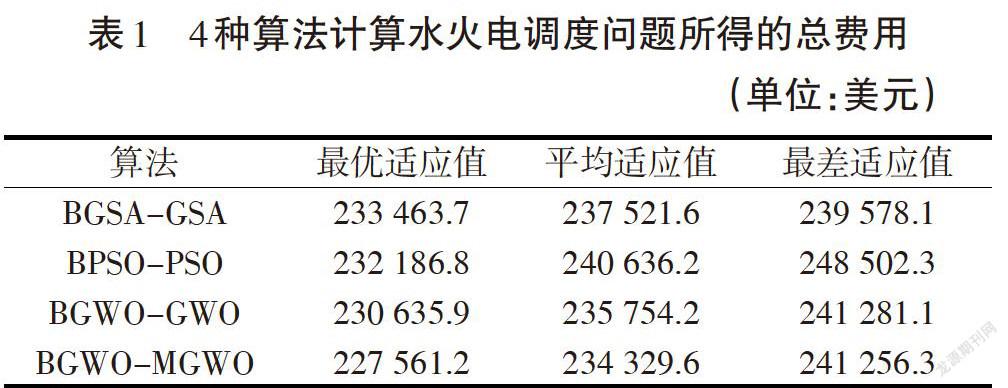
为了更好地观察修正后灰狼算法对解决本文调度问题的影响，除了与BGWO-GWO算法对比外，还与BPSO-PSO以及BGSA-GSA算法进行对比。为更好地观察计算效果，每种算法独立运行20次，计算结果如表1所示。

由表1可知，BGWO-MGWO算法得到的发电成本无论是最优值还是平均值，都要优于其他3种算法。这说明BGWO-MGWO算法在解决小火电调度问题时有着一定的优势。

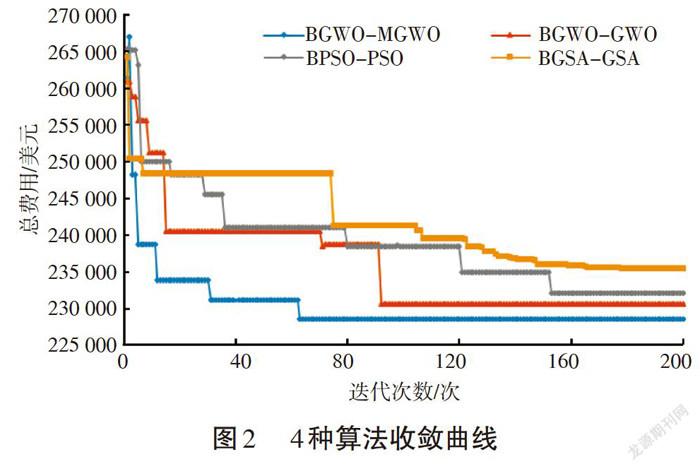
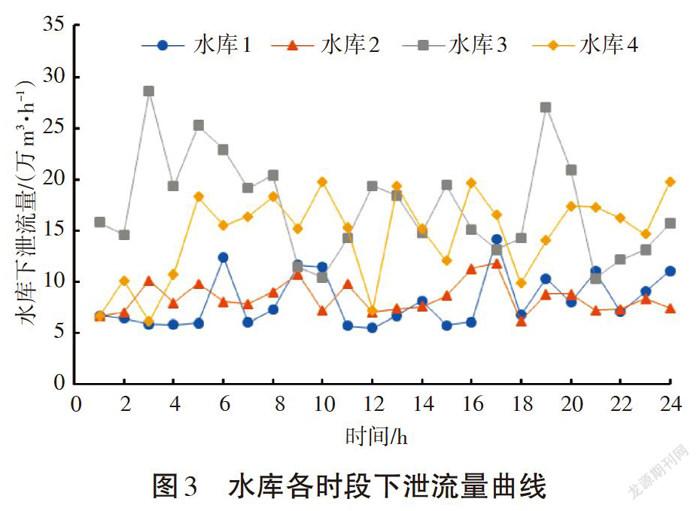
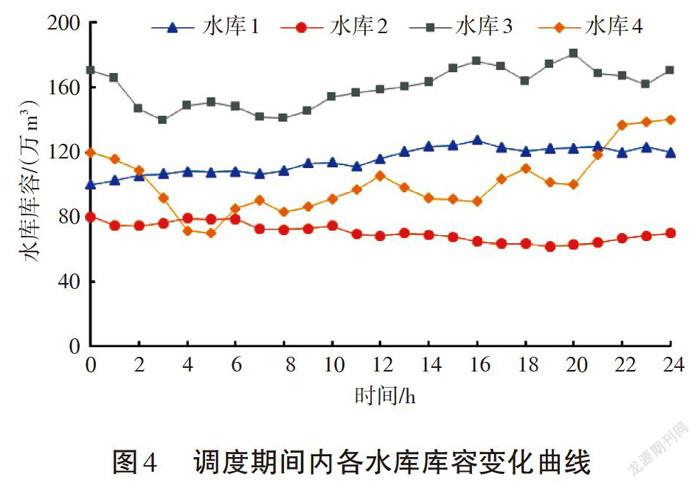
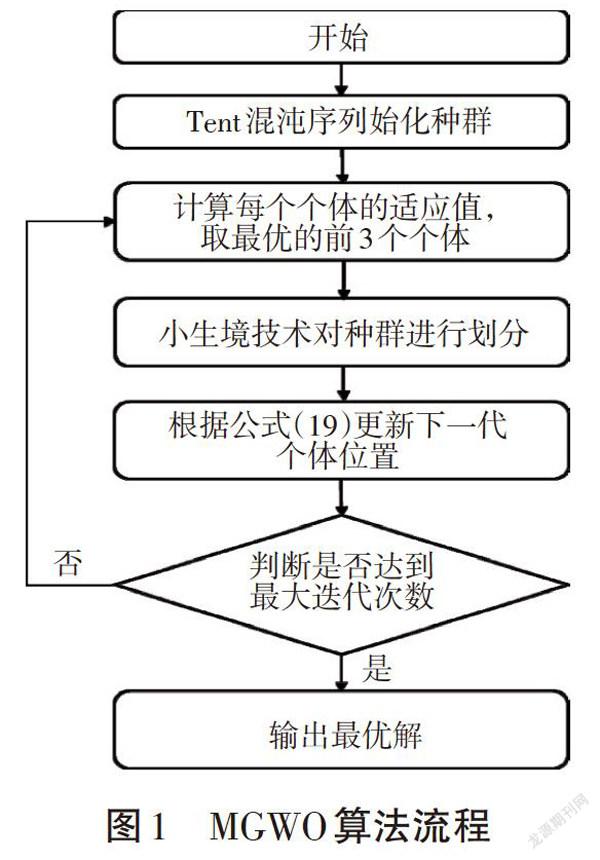
图2给出了4种算法的收敛过程曲线。由图可以看出，BGWO-MGWO算法计算的发电成本在前40次迭代中下降较快，在达到60代左右时，结果趋于平稳，表明算法寻找到了全局最优解。图3给出了调度期间内各个水库的下泄流量;图4给出了各个水库的库容变化曲线。

計算结果表明，在每个调度时段内的各水库下泄流量、水库初始库容、末库容以及其他各时段库容均符合约束条件。

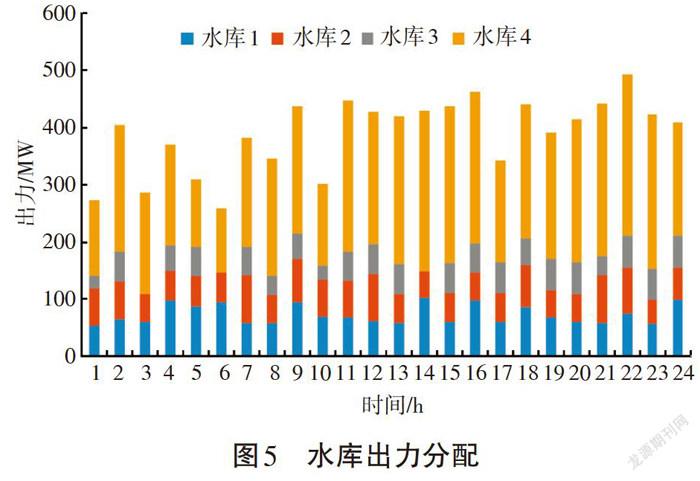
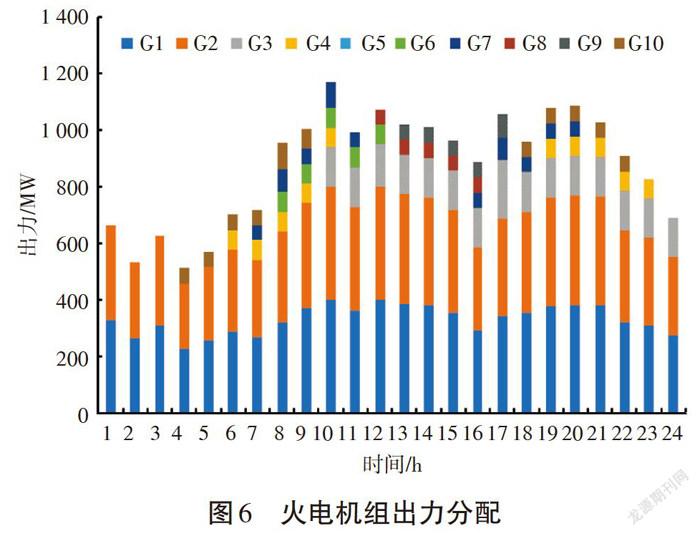
图5、6分别给出了调度期间内各梯级水库出力以及各火电机组出力分配情况。结合文献[13]中各约束条件可看出，在整个调度期间内，各火电机组出力始终保持在约束范围之内，并且所有火电机组的连续开关机时间均满足约束要求。由于负荷的变化以及水电站的调节能力不足，小型火电机组开停机费用低，在保证总出力的前提下，保证大型火电机组处于常开状态，小型的火电机组在没有违反开停机约束的情况下，开关机操作是合理的。再结合文献[14]中火电机组发电费用系数以及冷、热开机费用即可计算出目标函数值，经过验算与调度方案值相等。因此本文给出的调度方案是合理有效的。

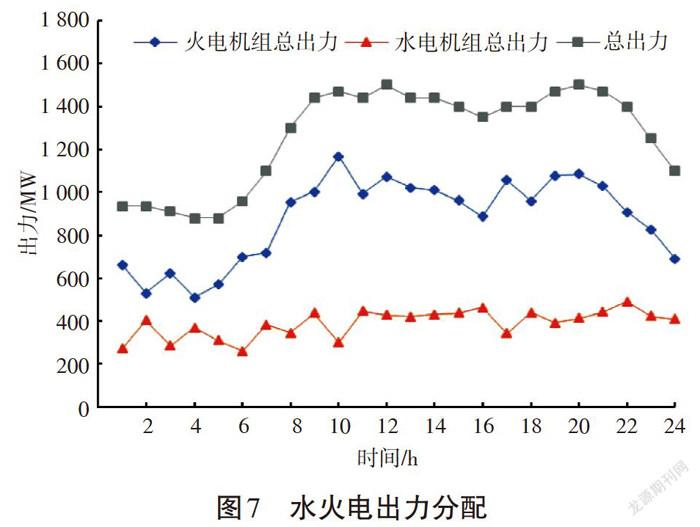
图7给出调度期间内水电站总出力、火电机组总出力以及发电系统总出力。由图7可以看出，发电系统总出力与每个调度时段给定的负荷一致。证明了该调度方案的合理性。

5 结语

本文对含有火电机组组合的水火电系统短期优化调度问题开展研究。对调度问题进行数学建模，明确模型目标函数以及发电系统内各式约束条件。深入研究灰狼算法并提出修正策略。然后针对标准灰狼算法的不足，引入混沌初始化、小生境技术以及混合粒子群技术对标准灰狼算法进行修正处理。

由于调度问题包含连续性决策变量（水库下泄流量）及离散型决策变量（火电机组组合），因此利用BGWO-MGWO组合优化算法对两种不同类型的优化问题同时进行优化求解。通过仿真实验，4种不同算法计算结果表明，BGWO-MGWO算法计算得到的平均费用相较BPSO-PSO、BGSA-GSA、BG-WO-GWO分别降低了26.2‰、13.4‰、6‰。因此，修正后的算法在解决水火电调度问题上具有一定的优势。

参考文献：

[1] 中华人民共和国国务院，国家中长期科学和技术发展规划纲要（2006-2020）[R].北京：中华人民共和国国务院，2006.

[2] 国家能源局.水电发展“十三五”规划（2016-2020年）[R].北京：国家能源局，2016.

[3]Shapiro A，Tekaya W， da Costa J P，et al.Risk neutraland risk averse stochastic dual dynamic programmingmethod[Jl. European Joumal of Operational Research，2013.224（2）：375-391.

[4]Santhi R K，Subramanian S.Adaptive Binary PSO basedunit commitment[J]. Intemational Journal of ComputerApplications， 2011， 15（4）： 1-6.

[5]邱天怡，基于粒子群算法的水火电力系统负荷优化分配[J].电气开关，2017（6）：28.

[6]Tian H， Yuan X， Huang Y， et al.An improved gravita-tional search algorithm for solving short-term economic/environmental hydrothermal scheduling[Jl. Soft Com-puting， 2015， 19（10）： 2783-2797.

[7]Li C，Zhou J，Lu P，et al.Short-term economic environ-mental hydrothermal scheduling using improved multi-ob-jective gravitational search algorithm[J].Energy Conver-sion and Management， 2015， 89： 127-136.

[8] 刘波，王凌，金以慧.差分进化算法研究进展[J].控制与泱策，2007， 22（7）：721-729.

[9]黄迪，徐刚，向红艳，等.基于改进差分进化算法的水火电短期优化调度[J].水力发电，2017， 43 （5）：76-80.

[10]Rajan C C A.Hydro-thermal unit commitment problemusing simulated annealing embedded evolutionary pro-gramming approach[J].Intemational Journal of Electri-cal Power& Energy Systems， 2011， 33 （4）： 939-946.

[11]Mirjalili S，Mirjalili S M， Lewis A.Grey Wolf optimiza-tion[J]. Advances in Engineering Software， 2014， 69（7）：46-61.

[12]单梁，强浩，李军，等.基于Tent映射的混沌优化算法[J].控制与决策，2005，20（2）：179-182.

[13]Lu S，Sun C，Lu Z.An improved quantum-behaved par-ticle swarm optimization method for short-term com-bined econormc emission hydrothermal scheduling[Jl.Energy Conversion and Management， 2010， 51 （3）：561-571.

[14]Dieu VN， Ongsakul W. Ramp rate constrained unit com-mitment by improved priority list and augmented la-grange hopfield network[Jl. Electric Power SystemsResearch， 2008， 78（3）：291-301.