基于Matlab对“电池剩余放电时间预测”问题的拓广研究
李双 谭杰明 强佳伟 吴将斌







摘要:超级电容器(supercapacitor)作为一种新型储能软件在实际生活中被广泛使用,在实际应用中,最重要的就是超级电容器在某工作环境下的续航能力以及寿命的长短。如今,对于数据的挖掘越来越深入,因此数据的预测分析显得尤为重要。本文通过对已有数据进行曲线拟合,利用Matlab强大的绘图功能对超级电容器的剩余放电时间和寿命进行合理预测,找到拟合度较高的曲线。结果表明,指数函数f(x)=aebx对超级电容器进行放电拟合预测结果最优,幂函数f(x)=axb+c对超级电容器寿命拟合预测结果最优。
关键词:放电时间预测;最小二乘法;数据拟合;MATLAB软件
1引言
电池作为日常生活中重要的能量来源,放电是电池最基本最核心的特性,对于电池剩余放电时间进行预测十分必要。超级电容器具有许多优越的性能,例如:质量轻、功率密度高、环境友好等。基于以上特点,超级电容器的应用范围将会越来越大,于是对于超级电容器的放电时间预测显得尤为重要。2016年高教社杯全国大学生数学建模竞赛C题为铅酸电池剩余放电时间预测问题,本文将C题中的铅酸电池拓广到超级电容器领域,建立超级电容器放电的模型,预测超级电容器的放电时间,希望为工业用电或日常用电提供参考。
2超级电容器放电模型
超级电容器(supercapacitor)作为一种通过极化电解质储能的元件,经常应用于太阳能能源系统、风力发电系统、新能源汽车、军事、医用器械等重要领域,推动了社会的发展。
2.1 超级电容器放电曲线拟合
为了确定超级电容器的放电曲线函数,我们选取某一电流强度下,工作电压为[1.5V,5.0V]的超级电容器单体。在实际操作中,如果要保证负载电路长期稳定工作,就需要保证负载电压长期稳定,所以采用PI调节的Boost升压电路来保证电压的稳定输出[1]。
实验中所采用的超级电容器从5V开始放电,测量其放电5小时后,超级电容器输出的电压值。利用放电采样数据的散点图进行拟合得到放电曲线的函數。
2.1.1多项式函数拟合
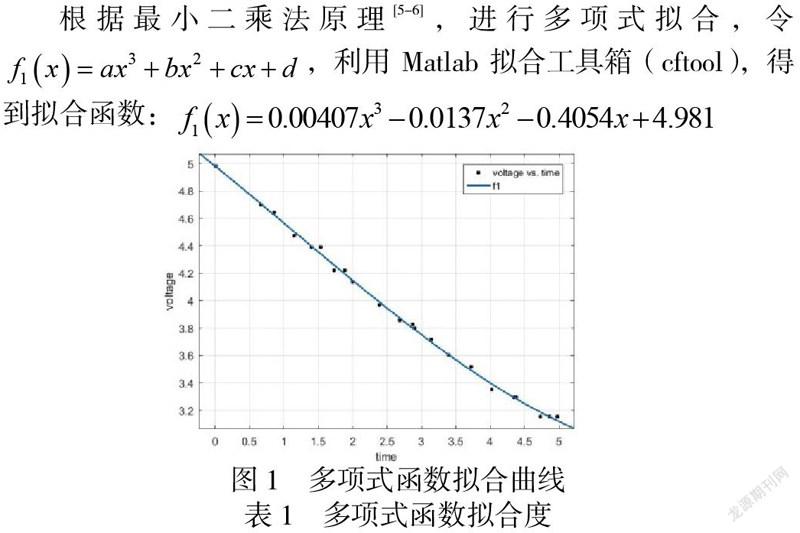
根据最小二乘法原理[5-6],进行多项式拟合,令,利用Matlab拟合工具箱(cftool),得到拟合函数:
从表1中看到确定系数R2大于0.99,而和方差与标准差均小于0.1,说明多项式模型拟合程度较好,可用于放电时间预测。
选择最高次项为3次的多项式函数来拟合最为恰当。次数过低,呈现出基本的整体趋势,损失了部分局部信息,呈现欠拟合状态;次数过高,则过于注重局部信息,呈现过拟合状态。
2.1.2指数函数拟合
利用指数函数进行拟合,令,使用Matlab拟合工具箱(cftool)进行拟合,得到函数
从表2中看到确定系数R2大于0.99,而和方差与标准差均小于0.1,说明指数模型拟合程度较好,可用于放电时间预测。
由上述得到的函数和曲线图像以及特征数可知,多项式函数拟合与指数函数拟合所得结果在放电前5小时无明显差距,下面进行数据预测来选取较优曲线。
2.2超级电容器放电时间预测
根据上述两函数,对5-10小时的放电电压进行预测,并画出放电曲线,其中,x轴代表放电时间,y轴代表放电电压,从x=0开始,至x=10结束,按照间隔不大于0.001提取样本点,画出曲线。
2.2.1多项式函数预测
显然,超级电容器的放电电压无法随放电时间的增大出现先降后升的情况,7小时后的曲线趋势显然不符合实际,多项式函数预测存在明显缺陷。
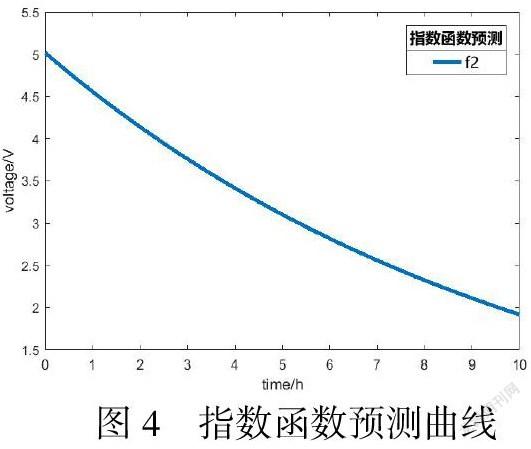
2.2.2指数函数预测
指数函数的预测曲线呈单调递减趋势,与电容器实际放电电压进行比较,数据与实验数据吻合度较高,下面考察该指数模型的一阶差分比率[2]。
该模型的一阶差分比率大致相等,符合指数曲线模型的数字特征,所以超级电容器的放电曲线模型可以选用模型:
超级电容器放电电压随着时间的推移呈现指数形式逐渐放缓的衰减,假设某超级电容器的初始放电电压为a,那么随着时间的推移其放电电压按照指数形式的下降,计算公式就是式f(x),其中b<0。
3、超级电容器寿命预测
超级电容器的寿命预测对于超级电容器的日常维护、更换具有重要的参考价值。定期对电路元件进行维护和保养,可以很大程度上避免由于检修不及时造成的人身安全和财产损失。
对超级电容器进行充放电,发现电容衰减曲线与幂函数保持一致[3],利用Matlab对电容衰减曲线进行拟合以便确定电容衰减到某一值时的循环次数。
3.1 超级电容器寿命曲线拟合
用幂函数进行拟合,得到如下函数以及曲线图像:
从表4中看到确定系数R2接近1,而和方差与标准差均较小,说明幂函数模型拟合程度较好,可用于超级电容器的寿命预测。
3.2 超级电容器寿命预测
利用f3对超级电容器的寿命进行预测,得到如下曲线,
4、总结
超级电容器的放电曲线较好地符合指数模型,超级电容器的寿命与幂函数保持一致,这两种曲线比较符合实际,误差较小,合理运用这两种曲线模型可以很好地对超级电容器的放电时间、寿命进行预测。
参考文献:
[1]潘曙光,董庆远,刘香.超级电容器充放电控制策略的研究[J].电器与能效管理技术,2018(03):20-24.
[2]张登奇,彭仕玉.差分方程的解法分析及其MATLAB实现[J]. 湖南理工学院学报.2014(03)
[3]刘恒洲,许雪成,卢向军.超级电容器循环寿命的预测[J].电池,2018,48(03):159-162.
[4]王庆.铅酸电池剩余放电时间预测模型[J].山东工业技术,2016(21):75.
[5]李丽丹.基于MATLAB的离散数据最小二乘拟合[J].辽宁工程技术大学学报(自然科学版),2011,30(S1):202-204.
[6]陈希孺.最小二乘法的历史回顾与现状[J].中国科学院研究生院学报,1998(01):5-12.
作者简介:
李双(1999-),女,陕西师范大学本科生。
谭杰明(1997-),男,陕西师范大学本科生。
强佳伟(1999-),女,陕西师范大学本科生。
吴将斌(1998-),男,陕西师范大学本科生。

