寿险公司资产负债管理模型研究
高天








摘 要:建立一个引入保险产品缴费期限结构的多期动态资产负债管理模型,改善以往研究中对负债端的简化,使得资产配置决策与产品销售决策联系紧密。同时,根据多数假设对该模型进行实证研究,结果显示:定期债券作为寿险公司主要投资品种保持了较高的配置比例,而股票基金配置比例受股市景气度影响较大;期缴产品为寿险公司产品销售的主力,而趸缴产品受股市景气度影响较大;相较于股票基金投资收益率,期望利润现值对定期债券市场利率的变动更为敏感;股票基金减持比例的变化同时影响资产配置及产品销售决策,寿险公司应主动加强股票资产配置的灵活性。
关键词:寿险公司;资产负债管理;多阶段随机规划;缴费期限结构
文章编号:2095-5960(2019)06-0056-10;中图分类号:F840.62;文献标识码:A
一、引言及文献回顾
近年来随着我国保险行业快速发展、险资投资渠道不断拓宽、外部市场环境也变得日趋复杂化,使得保险公司资产负债结构不匹配问题频出,保险公司亟须构建适合自身需求的资产负债管理体系。正是在这种背景下,中国银保监会于2018年2月28日向相关保险机构发布了《保险资产负债管理监管规则(1-5号)》。监管规则分为量化评估和能力评估,根据评估结果,保险监督管理委员会将对保险公司实施“软约束”的差别监管,积极引导保险公司主动加强资产负债管理能力的提升。对于所有保险公司来说,资产负债管理能力成为其在保险业稳健经营发展的基础能力和核心竞争力。因此,在这样的行业发展需求和监管背景下,如何设计出一套科学合理的资产负债管理模型框架成了亟待解决的问题。
资产负债管理(Asset - Liability Management,ALM)理论的研究历经多年发展已愈发完善,所囊括的内容较多,涉及保险公司战略规划、业务运营、投资管理、风险管理、绩效管理等方方面面。20世纪90年代以前,由于保险公司面临的金融环境较为简单,保险产品类型也较少,因此其所面临的经营风险也相对单一,其资产负债管理目标主要是应对利率风险。Frank M. Redington(1952)提出[1],保险公司应使资产和负债的平均剩余期限相等,即经典的久期免疫理论。随着金融市场和保险行业的不断创新发展,损失往往不是单纯由利率风险导致,此时学术界普遍认为保险公司应对多种风险因素进行全面管控,于是伴隨着计算机计算能力的提升,研究者也尝试将更多更复杂的优化方法引入保险公司资产负债管理研究中,考虑的因素越来越复杂,同时也将单期静态模型拓展为多期动态模型。其中随机规划因其能够解出多期多变量问题在未来不确定环境下的数值解,因此在保险公司资产负债管理领域得到了广泛的应用。其中具有代表性的成果为:Kusy和Ziemba(1986)将随机优化与资产负债管理结合,设计出一个简单补偿的多期随机线性规划模型。[2]Carino等(1994,1998)为日本Yasuda Kasai财产保险公司专门开发了Russell-Yasuda Kasai模型,该模型是一种离散多期随机规划模型,能够给出保险公司资产负债管理最优策略。[3][4][5]Yasuda Kasai公司应用该模型,成功使公司在两年的时间里获得大量的超额收入。Mulvey等(2000)在Russell-Yasuda Kasai 模型框架上引入了一组决策规则,提出一种改进的基于随机规划和决策规则的保险公司资产负债管理模型。[6] Consiglio等(2006,2008) 基于最低保证利率、红利期权等产品特征,建立一种基于随机规划的能够最大化保险公司效用函数的资产负债管理,并利用英国的数据进行了实证研究。[7][8]
国内学术界由于起步较晚,因此在保险公司资产负债管理模型方面的研究主要基于随机规划方法。谢强等(2009)建立了基于多目标规划的保险公司资产负债管理模型,然而其模型仅为单期模型,未考虑保险公司长期持续经营所需面对的跨期影响。[9] 余洋(2010)设计了一种基于随机动态规划的资产负债管理模型,其将违反约束条件的惩罚成本引入目标函数。[10] 李秀芳等(2014)基于保险公司多目标建立了资产负债管理模型,然而该模型假设负债端结构固定,且受制于多目标规划特性,仅给出一组pareto非劣解。[11] 瞿栋(2015)在其论文中利用 Black-Litterman 模型和多元 Copula-CVaR 函数建立了基于风险预算理论的保险公司资产负债管理模型。[12] 李秀芳等(2016)考虑了寿险公司资产负债管理目标之间的多层次属性,提出了一种基于二层规划的寿险公司资产负债管理模型,但该模型仅能在规划期初对资产端及负债端进行决策,经营过程中资产负债结构无法调整,对实际经营决策参考意义有限。[13] 何宇佳等(2016)建立了一种包含资产配置比例和分红率的生死两全分红险账户资产负债管理模型,该模型在负债端仅对分红率进行决策,无法对负债端产品销售比例进行优化。[14] 唐博(2018)引入分红寿险现金分红机制,提出了一种基于多目标规划的寿险公司分红险账户资产负债管理模型,该模型实现了投资资产配置的动态决策过程,然而局限性在于其仅能对资产端进行决策。[15]
通过对上述研究成果的梳理我们发现,现有研究成果大多对负债端的设定相对简单。大多数文献中,除期初给定的保单外,简单假定每期没有新承保保单,负债端现金流结构为事先给定,因此其模型退化为负债端固定的投资策略优化模型;而一些文献中,虽然考虑了负债端决策,然而为了简化问题,假定保险产品具有完全相同的特征,且负债端结构为模型事先给定,仅对分红率等参数进行决策。而在实际经营过程中,除了资产配置决策外,往往还需要考虑承保业务的期限结构特征,对具有不同缴费方式的保险产品在每期进行结构优化,以满足偿付能力、流动性和久期缺口等约束,并实现寿险公司的经营目标,否则难免造成投资业务与承保业务的脱节,导致资产负债管理的作用大打折扣,并成为保险公司未来发展的掣肘。因此,本文创新性地引入了不同缴费期限的保险产品,并在此基础上建立了基于随机规划方法的以资产配置比例及不同缴费期限产品新单销售比例为各期决策变量的寿险公司资产负债管理模型,并进行实证分析,以期为寿险公司建立更加科学合理的资产负债管理体系提供模型参考,在实现经营目标的同时,增强寿险公司对抗及管控各类风险的能力。
二、基于随机规划的寿险公司资产负债管理模型
(一)负债端建模
1.有效保单数量
我们假定寿险公司仅销售两种定期寿险产品,寿险公司在每一个决策年期初对产品的新单销售量进行决策,则有:
其他变量计算方法类似,在此不再赘述。
(二)投资端建模
为了简化讨论,假设寿险公司可配置的投资资产为一种权重不变的股票指数投资基金及一种定期债券。所有投资决策发生在每期初,股票基金在每期末按照固定比例卖出,债券在到期前不卖出,可购买的份额可以无限细分。所有资产无违约风险,且买卖均无交易费用。
1.股票基金资产
股票基金相关动态变化关系如下:
2.定期债券资产
对于定期债券资产,我们假定其平价发行,会计上划分为持有至到期投资。则定期债券相关变量的动态变化关系如下:
(三)寿险公司资产负债动态变化过程
为了简化讨论,我们假设寿险公司每期资产仅由现金、定期债券及股票基金资产构成,负债仅为寿险责任准备金。假定寿险公司不分红、不转增股本,不考虑税收因素,则净资产为实收资本和累计净利润之和。一个简化的寿险公司资产负债表如表1所示:
至此,我们已经对寿险公司的基本经营过程完成了建模刻画。在此基础之上,我们将建立基于随机规划的寿险公司资产负债管理优化问题。
(四)约束条件
模型约束条件主要由五部分组成:(1)偿付能力约束;(2)久期缺口约束;(3)资金运用约束;(4)流动性约束;(5)其他约束。
3.资金运用比例约束
银保监会在2014年发布的《关于加强和改进保险资金运用比例监管的通知》中,将保险资金可以投资的品种归为五大类:流动性资产、固定收益类资产、权益类资产、不动产类资产及其他金融资产。为了便于讨论,本文建模仅选取了现金、股票基金及定期债券分别作为流动性资产、权益类资产及固定收益类资产的代表。参考该文件,令每一个决策期投资股票基金的账面价值不高于寿险公司总资产的30%,即SiAi≤30%。
4.流动性约束
寿险公司在每期末支付完所有费用及支出后,现金在期末总资产中的占比需达到5%以上,即C1iAi≥5%。
5.其他约束
本文中假设每类投资资产每期均不可卖空,因此有Si≥0,Bi≥0。另外由于保险公司经营战略的剧烈变化不利于公司的稳健有序发展,因此需对各决策变量在各期间的波动幅度进行限制。因此,我们假定对各期决策变量xki有:
(五)目标函数
由于约束条件中已经考虑了对投保人利益的保障及对利率、市场和流动性风险的防范,且净利润能够有效反映负债端及投资端之间的平衡关系,因此我们假设保险公司资产负债管理的目标为在不同经济情景下最大化期望净利润的现值。即:
(六)模型建立
基于前述负债端、投资端和财务模块,我们将约束条件及目标函数整合,即得到本文所建立基于随机规划的寿险公司资产负债管理模型:
三、实证研究
(一)参数假设
1.重要模型参数
对于本文所述模型,权衡考虑计算复杂度和模型代表性后,本文将模型决策期限T设定为10期。对于股东注资,我们假定股东将在第1和5期初以增资的形式分别投入现金750,000,000元。同时,结合行业数据,本文将寿险公司风险贴现利率ν设定为11.5%。
2.负债端参数
本文假定寿险公司经营两种定期寿险产品,两种产品期初最大可售保单数量ini1、ini2均为1,000,000份,年均增长率g为15%。为简化讨论,假设所有产品投保人均为35岁男性,死亡率取自《中国人寿保险业经验生命表(2010—2013)》中非养老金业务男表。退保率如表2所示:
两种产品的保险期限NU为5年,产品1和产品2缴费期限N1P、N2P分别为3年期缴和1年趸缴。定价利率rpricing及准备金评估利率rreserve均为3.5%。件均保额AZ为1,000,000元。退保惩罚比例为20%。费用为当期保费的比例费用,费用率如表3所示:
件均保费通过资产份额定价法设定利润指标计算得出。设定利润指标:产品1、产品2要求利润现值需达到保费现值的比例分别为4%和1%。利潤测试所使用的折现率为产品定价利率rpricing。经过计算,产品1、产品2件均保费p1、p2分别为2,884.2元和5,990.5元。
3.资产端参数
对于可投资的定期债券,我们设定其到期期限为3年,票面利率为当期3年定期债券市场利率rbondi。由于本文模型将决策期间T设定为10期,利用Wind数据库,我们选取2010—2019年中债3年期AAA级企业债到期收益率月度数据在一年中取算术平均值(不足一年按已有数据平均计算,下同)作为数据来源。对于股票基金,结合各保险公司公开数据及专家访谈,本文将每期末股票基金卖出的比例θ设定为50%。对于股票基金投资收益率rstocki,我们以上证综合指数代表股票基金组合,同样利用Wind数据库,可计算得到2010—2019年上证综合指数年化投资收益率作为数据来源。我们以上述10期定期债券市场利率及股票基金投资收益率作为经济基础情景。在此基础上,为反映外部经济环境无法准确预测的可能变化,我们给出悲观情景和乐观情景。参考杨杰(2010)的实证研究成果[16],我们假定债市和股市之间存在“跷跷板效应”,即债券市场利率同股票投资收益率呈反向变动关系。悲观情景下,本文设定各期债券市场利率将平行提高1个百分点,受融资成本上升等影响,各期股票投资收益率则平行降低5个百分点;乐观情景下,受流动性充裕影响,我们设定债券市场利率将平行降低1个百分点,而各期股票投资收益率则平行提高5个百分点。综上,本文所选取的不同经济情景下的定期债券市场利率及股票基金投资收益率如图1、图2所示:
同时,我们假定寿险公司根据专家预测法得到悲观情景、基础情景及乐观情景出现的概率分布如表4:
(二)求解结果
本文使用Matlab(R2018a版本)对前述模型进行编程,并使用Global Optimization Toolbox中的相关函数对规划问题进行求解。求解结果如表5所示,参数动态变化情况见图3—图6。
根据求解结果可得到如下结论:
(1)从投资资产配置决策上来说,股票基金的配置比例各期间的波动幅度较大,在投资收益率为负的决策期幾乎没有配置,仅在投资收益率为正的决策期配置股票基金,这与股票基金投资收益率本身波动幅度较大直接相关。特别的,第5及10期股票基金配置比例较高,这主要是由于中国股市在2014年下半年至2015年上半年的大牛市以及2019年第一季度的反转带来的投资收益率大幅上升。虽然第1—5期寿险公司在乐观情景下的偿付能力及流动性均位于约束条件边缘,但由于第5期股东的增资为公司提供了大量资金,使得寿险公司在对应决策期能以较大比例投资于股票基金配置的同时不违反偿付能力及流动性约束条件。而对于定期债券,由于其对偿付能力的消耗较少,且债券市场利率波动幅度相比股票基金投资收益率较低,因此其配置比例始终保持在较高水平且波动幅度较小,这与寿险公司资产配置以固定收益类为主的行业现状也保持了一致。
(2)从产品销售决策上来说,期缴产品由于相比趸缴产品利润率较高,在同样的保险责任下,计提的寿险责任准备金相对也较少,因此其销售比例一直保持在较高水平。特别的,受第5期股东增资及股票基金在实现较高收益后及时减持的影响,使得寿险公司偿付能力及流动性水平大幅上升,导致第6—10期期缴产品销售比例更是明显上升。而对于趸缴产品,虽然本文中趸缴产品在利润率、准备金计提、偿付能力消耗等方面较期缴产品均处于劣势,但由于其能在承保首期初即收到全部保费,使得寿险公司能有更多额外资金投资于股票市场,因此趸缴产品的销售比例同股票基金配置比例高度相关,这意味着寿险公司在股票市场较为景气时,更愿意加大趸缴产品的销售力度。综上,在本文模型模拟结果中期缴产品属于寿险公司产品销售的中坚力量,其销售比例主要受偿付能力及流动性水平的限制影响,而趸缴产品则作为期缴产品的补充,其销售比例还受股票市场的景气程度影响。
(3)从偿付能力上来说,为最大化当期利润,第1-5期乐观情景下的偿付能力充足率均处于约束条件的边缘,从第6期开始偿付能力充足率明显提升,到第10期则再次明显下降。这主要是三方面因素导致:①第5期股东增资且股票基金实现了较高投资收益,使得寿险公司认可资产大幅增加;②第6-9期股票基金收益较低,使得寿险公司投资于股票基金的比例较低,导致市场风险最低资本较第5期明显下降,而第10期则反之;③受本文模型决策变量波动幅度约束影响,第6-10期寿险公司销售产品的比例无法达到理论极限,使得认可负债及保险风险最低资本的上升幅度明显低于认可资产。这种波动幅度的约束也符合中小型险企在实际经营中面临的代理人队伍及网点建设具有较长投入产出期,使得所销售产品(特别是保障型产品)难以快速拓展市场份额的行业现实。
(4)从久期缺口上来说,由于本文中寿险公司销售的产品保险期限均为5年,而定期债券到期期限为3年,因此负债端现金流出的久期明显更长,使得各期久期缺口均为负。由于期缴产品较趸缴产品现金流入久期更长,因此从第6期起,寿险公司适时调整了期缴和趸缴产品的销售比例,使得久期缺口仍然能够稳定在约束条件以内。
(三)敏感性分析
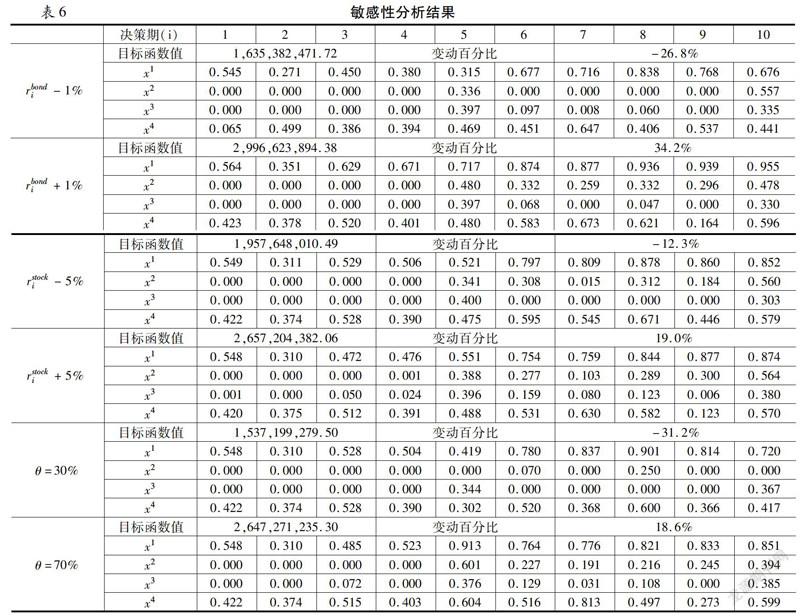
为了检验外部经济情景及股票基金期末减持比例的变化对最优策略的影响,本文对上述模型进行了单因素敏感性分析。以前述参数假设作为基准情形,保持其他参数不变,我们分别将各经济情景下各期定期债券市场利率rbondi增减1个百分点,将各期股票基金投资收益率rstocki增减5个百分点,将股票基金期末减持比例θ设置为30%和70%,观察对最优策略下目标函数值及各期决策变量取值的影响。求解结果如表6所示。
根据表6可以得到以下结论:
(1)对于定期债券市场利率rbondi的变动:①当rbondi降低1个百分点时,目标函数值相较于基准情形降低了26.8%,在股票基金投资收益率较低的决策期,寿险公司没有更好的投资资产用来替代定期债券,因此并未明显改变资产配置的比例,但是由于在乐观情景下因利率倒挂产生了利差损,因此在各期均减少了两种产品的销售比例;②当rbondi升高1个百分点时,目标函数值相较于基准情形提高了34.2%,由于寿险公司在基准情景下配置于定期债券的比例已经临近流动性约束上限,因此寿险公司无法进一步增加对定期债券的配置比例,但在各期均增加了两种产品的销售比例以把握债券市场行情。
(2)对于股票基金投资收益率rstocki的变动:①当rstocki降低5个百分点时,目标函数值相较于基准情形降低了12.3%,除第5、10期外,其余决策期股票基金投资收益率均较低或为负,因此寿险公司在此期间不配置任何股票基金资产,同时为优化资金使用效率,在第5期之后转而增加了定期债券的配置比例,由于流动性及波动幅度约束的限制,寿险公司基本未改变产品销售策略;②当rstocki升高5个百分点时,目标函数值相较于基准情形提高了19.0%,由于资金运用约束的限制,寿险公司难以进一步增加对股票基金的配置比例,但在第5期后均不同程度地增加了趸缴产品的销售比例以把握股票市场行情。
(3)对于股票基金期末减持比例θ的变动:①当θ为30%时,目标函数值相较于基准情形降低了31.2%,由于股票基金资产变现能力降低,使得资金运用比例及流动性均受负面影响,因此寿险公司相应减少了各期股票基金的配置比例,同时,股票基金在寿险公司账上的滞留消耗了更多偿付能力,使得寿险公司不得不降低负债端的销售比例,消耗偿付能力较多的趸缴产品更是受到显著影响;②当θ为70%时,目标函数值相较于基准情形提高了18.6%,由于股票基金资产变现能力升高,寿险公司则相应增加了各期股票基金的配置比例,同时由于及时减持带来的流动性改善,使得寿险公司还能够提高定期债券的配置比例,而对于负债端,由于减持比例升高导致投资端对偿付能力的消耗降低,因此寿险公司能够提高产品的销售比例。
四、结论与建议
为弥补现有寿险公司资产负债管理中对缴费方式研究的忽视,本文创新性地引入两种具有不同缴费期限的定期寿险产品,建立了一个在未来不同经济情景下,以寿险公司期望利润现值为优化目标,基于随机规划的多期动态资产负债管理模型。该模型能够改善以往研究所建立资产负债管理模型由于负债端相对固定退化为投资策略优化模型的问题,结合资产配置策略对具有不同缴费期限的保险产品进行销售策略优化。同时,本文根据参数假设对该模型进行了实证研究,并在投资配置、产品结构、償付能力和久期缺口四个方面分析了相关决策变量及其他关键指标的动力学特征,针对债券市场利率、股票基金投资收益率和股票基金期末减持比例的变动对目标函数及决策变量的影响进行了敏感性分析。
综上所述,本文所建立引入保险产品缴费期限结构的多期动态资产负债管理模型改善了以往研究中对负债端的简化,使得资产配置决策与产品销售决策联系更加紧密,对于寿险公司实际资产负债管理过程具有一定的参考价值。寿险公司可结合自身及市场数据参考本文所建立资产负债管理模型,围绕经营战略目标科学制定相互关联的资产配置策略及产品销售策略,并根据外部经济环境的变化,适时调整大类资产配置及产品结构。同时,寿险公司应降低股票资产的持有时间(比如降低对具有锁定期股票的投资),以保持股票资产具有充足的变现能力并增加寿险公司负债端决策的灵活性。
参考文献:
[1]Redington F M. Review of the Principles of Life-Office Valuations[J]. Journal of the Institute of Actuarie, 1952, 78(3): 286-340.
[2]Kusy M I, Ziemba W T. A Bank Asset and Liability Management Model[J].Operations Research, 1986, 34 (3) :356-376.
[3]Carino D R, Kent T and Myers D H, et al. The Russell-Yasuda Kasai Model: an Asset/Liability Model for a Japanese Insurance Company Using Multistage Stochastic Programming[J]. Interfaces, 1994, 24(1) :29-49.
[4]Carino D R, Myers D H, Ziemba W T. Concepts, Technical Issues, and Uses of the Russell-Yasuda Kasai Financial Planning Model[J]. Operations Research, 1998,46(4) :450-462.
[5]Carino D R, Ziemba W T. Formulation of the Russell-Yasuda Kasai Financial Planning Model[J]. Operations Research, 1998, 46(4) :433-449.
[6]Mulvey J M, Gould G and Morgan C. An Asset and Liability Management System for Towers Perrin-Tillinghast[J]. Interfaces, 2000, 30(1):96-114.
[7]Consiglio A, Cocco F and Zenios S A. Asset and Liability Modelling for Participating Policies with Guarantees[J]. European Journal of Operational Research,2008, 186(1):380-404.
[8]Consiglio A, Saunders D, Zenios S A. Asset and Liability Management for Insurance Products with Minimum Guarantees: the UK Case[J]. Journal of Banking & Finance, 2006, 30(2) :645-667.
[9]解强, 李秀芳. 基于多目标规划的保险公司资产负债管理[J]. 现代管理科学,2009(10):17-27.
[10]余洋. 我国财产保险公司资产负债管理研究——基于动态随机规划法[D]. 武汉: 武汉大学, 2010.
[11]李秀芳, 景珮. 基于多目标规划的寿险公司随机资产负债管理研究[J]. 经济管理,2014(3):108-117.
[12]瞿栋. 基于风险预算理论的保险资产管理路径研究[D].北京: 对外经济贸易大学, 2015.
[13]李秀芳, 毕冬, 陈孝伟. 基于二层规划的寿险公司资产负债管理研究[J]. 保险研究, 2016(3):73-83.
[14]何宇佳, 陈秉正, 陈泽. 分红型保险产品经营分析——双驱动型动态最优资产负债管理视角的探讨[J]. 投资研究,2016, 35(6):72-85.
[15]唐博. 分红寿险资产负债管理优化方法的改进[J]. 保险研究, 2018(7):60-70.
[16]杨杰. 我国利率对股票价格指数影响的实证分析[J]. 金融经济,2010(2):95-97.

