不同炸药对花岗岩不同位置爆破的数值模拟
李婷婷,费爱萍,牛雪峰,朱春宇
(1.吉林大学地球探测科学与技术学院,长春 130026;2.辽宁科技大学土木工程学院,辽宁 鞍山 114051)
矿山爆破时炸药与岩石参数的不合理匹配,导致炸药利用率低和爆破效果不理想,数值模拟可以辅助优化爆破参数进而解决此问题。为提高爆破效果,国内外学者利用ANSYS/LS-DYNA做过大量研究。吴贤振等[1]对炮孔间距和延时时间进行模拟匹配,寻求最佳减振效果;刘洪榕等[2]对多点同步起爆条件下,圆柱形传爆药柱,8个点起爆和4个点起爆的效果进行数值模拟;楼晓明等[3]提出延时时间为25 ms时,降振最为明显;梁瑞等[4]对5种不同空气间隔装药结构进行了数值模拟;张大宁等[5]对大孤山进行了双孔延时爆破模拟;王冬兵等[6]为降低大块率采用水间隔装药进行数值模拟;南江等[7]利用LS-DYNA讨论爆破量与围岩破坏半径的关系;顾文斌等[8]从阻抗匹配的角度分析装药结构对爆破振动的影响;ZHAO Jianjian等[9]利用LS-DYNA研究了延时时间下的双孔爆破效果。上述研究成果主要从延时时间、装药结构、波阻抗等角度对爆破方案进行调整,从未考虑改变炸药的使用种类,实际上爆破中炸药品种的选择与岩石的匹配对爆破效果也是至关重要的。为此,利用ANSYS/LS-DYNA对特定矿山岩种与炸药匹配进行数值模拟,同时优化布孔参数,解决炸药利用率低和爆破效果不理想的问题。
1 建立数值模型
首先,将同种炸药在炮孔间距不同时与花岗岩进行匹配;其次,将10种炸药在炮孔间距相同时分别与花岗岩进行匹配,共有50种双孔爆破匹配方案,每种方案中的两个炮孔分别记为第1炮孔和第2炮孔,进而每种方案需从4个方面提取应力时程数据:两个炮孔间中垂线方向、第1炮孔水平线方向、第1炮孔中垂线方向以及第2炮孔中垂线方向,应力时程数据总共200种。最后通过比较爆破后岩石的爆破范围与铲状,寻求最佳匹配方案。
1.1 算法及建模条件
ANSYS/LS-DYNA是一种以Largrange算法为主,兼有ALE和Euler算法,以显示求解为主兼有隐式求解功能的大型非线性有限元程序[10]。本次数值模型由炸药和岩石组成,岩石介质采用拉格朗日算法建模,考虑到冲击波在固体矿石的传播过程中,涉及到两种不同性质的物态接触问题,并且同时涉及高幅值的冲击波。为避免大变形单元的产生,采用多物质ALE算法,可提供精确、稳定、守恒而且单调的数值计算结果;炸药与岩石间采用共节点,边界设定为无反射边界条件。据实践经验,对长度近10 m岩体采用双孔布设进行模拟。
为了使模拟结果能够更真实、准确地反映双孔爆破对岩石介质的影响作用,规定双孔爆破数值模拟计算模型的建立应遵循以下4点[5]:①假设爆轰产物的膨胀是绝热过程;②不考虑爆轰气体的渗流作用;③假设岩石介质连续;④采用中心点起爆方式起爆。
1.2 计算模型
采用2D Solid 162建模,爆破介质模型尺寸为1 000 cm×1 000 cm(见图1)。两个炮孔直径20 cm,孔距从380~780 cm(380、480、580、680、780)分别建模,数值模型采用cm-g-s单位制,共划分两个材料部分,60 552个节点,61 269个计算单元。
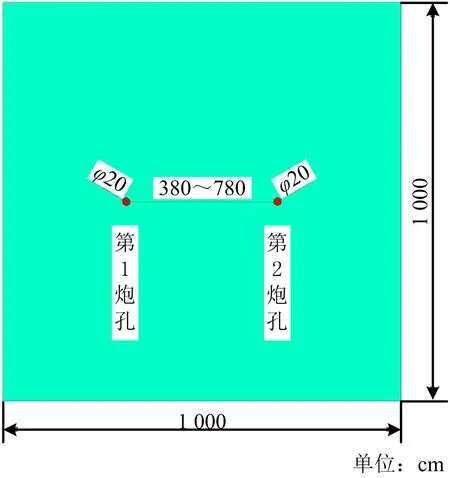
图1 双孔爆破有限元模型(1 000 cm×1 000 cm)Fig.1 Double hole blasting finite element model
1.3 材料模型
1)炸药模型。采用高能炸药引爆燃烧材料模型(MAT_HIGH_EXPLOSIVE_BURN)来描述炸药的性质,具体方程[11]如下:
F=max (F1,F2)
(1)
(2)
(3)
式中:Vcj是c-j相对体积;t为当前时间;t1为爆轰波从起爆点传至当前单元形心处所需最短的时间。
若F>1,则取F=1。
炸药爆炸后爆轰产物流动行为将导致其压力与体积的变化,可采用JWL(Jones-Wilkins-Lee)状态方程[11]进行计算:
(4)
式中:p为压力;A、B、R1、R2、ω为材料常数;V为相对体积;E0为初始比内能。
把酒临风:科技创新不是一个急功近利的问题,在中国你成功之后别人可能会抄袭,但在法治国家不行,你抄袭就重罚你,谁都不能随便侵犯他人,如果真做到这一点,我们的科技创新就能产出更多成果。也就是说完善的财产保护制度,才能让大家看到技术创新暴富的可能性。
取10种炸药与岩石进行性能匹配,所用炸药材料参数和状态方程参数如表1所示。
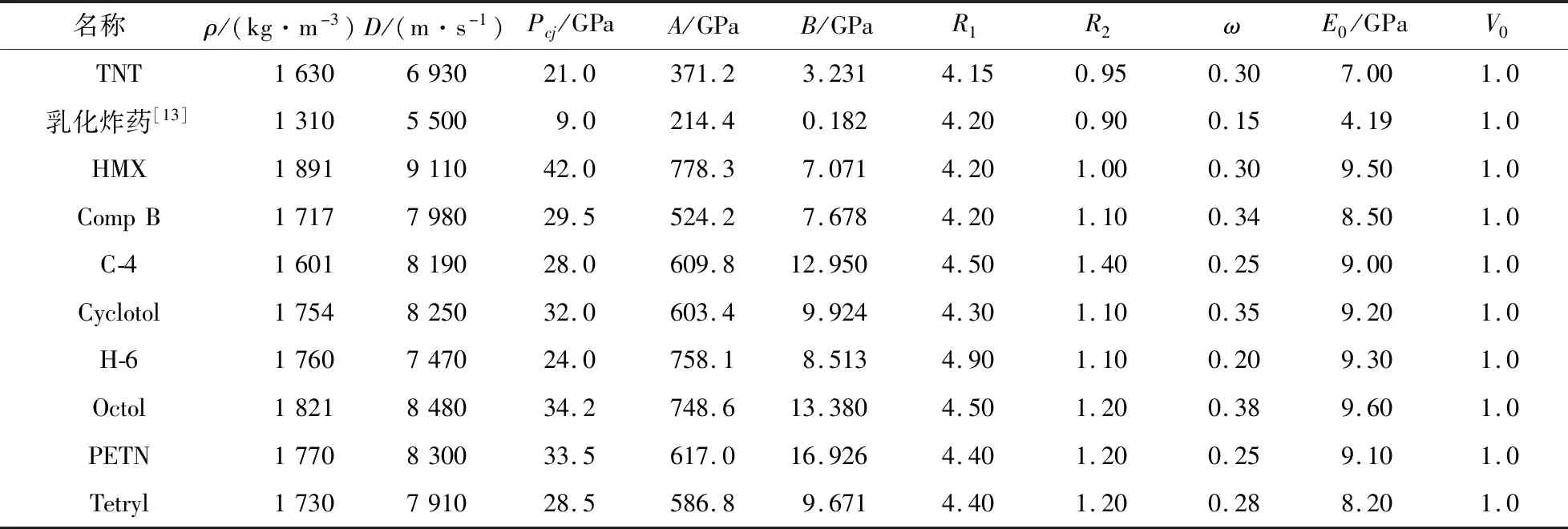
表1 炸药材料参数和状态方程参数[12]Table 1 The parameters of explosives materials and EOS
2)爆破介质模型。采用各向同性双线性弹塑性模型(MAT_PLASTIC_KINEMATIC)来描述爆破介质的本构关系。此材料考虑了岩石介质的弹塑性性质,并且能够对材料的强化效应(随动强化和各项同性强化)和应变率效应加以描述,同时带有失效应变[14],花岗岩力学性能如表2所示。

表2 岩石力学参数[15]Table 2 Rock mechanics parameters
1.4 数值计算时间
2 模拟计算
2.1 应力云图
爆破过程中应力均以波的形式传播,通过对双孔爆破的数值模拟,可在动态的爆破过程中观察爆破介质因炸药爆炸形成的应力云图。通过数值条的变化,了解爆破中各处的受力情况,并拾取特定位置的单元,观察整个爆破模拟过程中的应力变化。将10种炸药分别在孔距为380、480、580、680、780 cm的条件下共进行50次双孔爆破数值模拟运算,以炸药种类为TNT、孔距为380 cm时的爆破云图为例进行分析,其应力云图如图2所示。
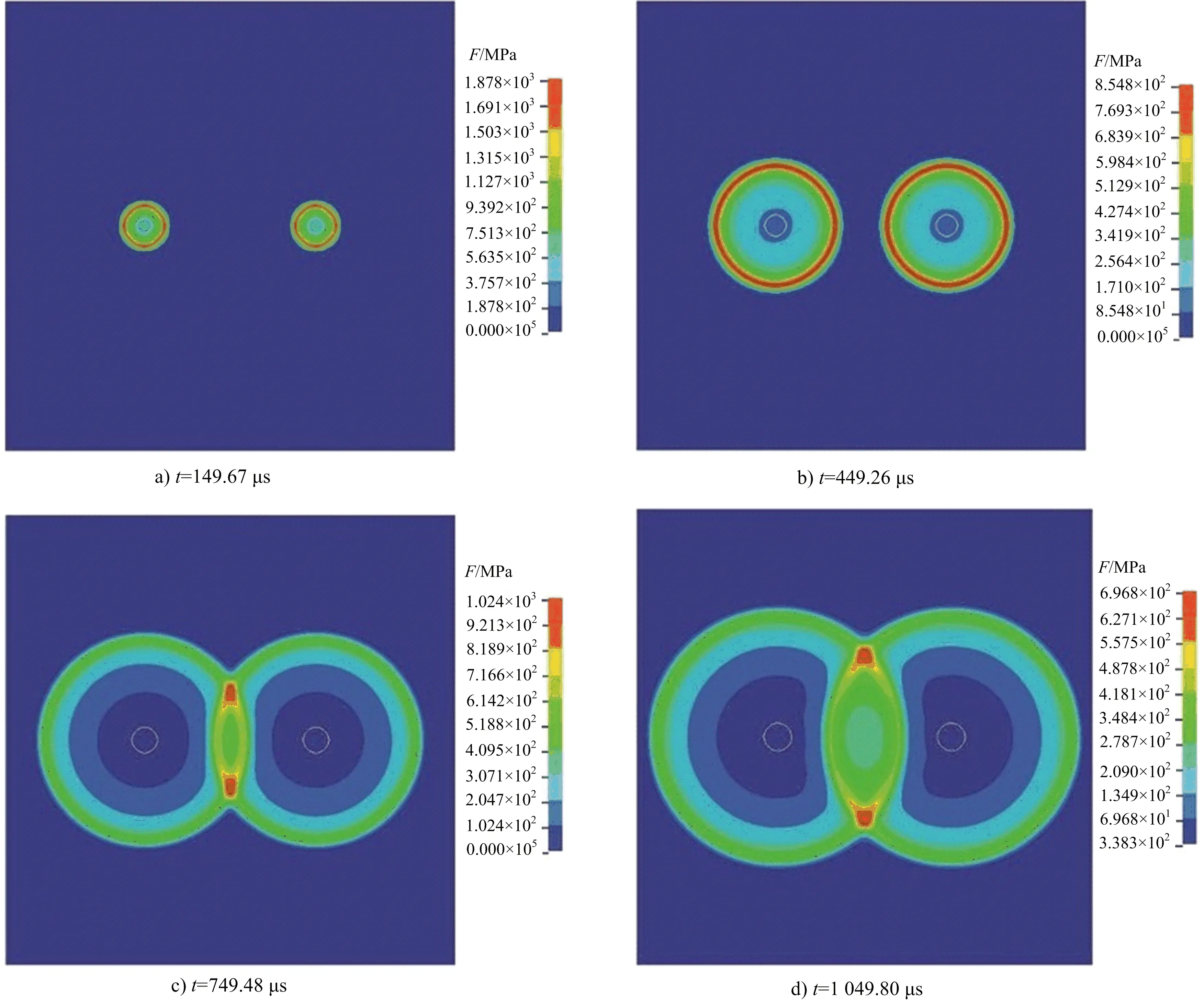
图2 双孔模型同时起爆应力云图Fig.2 Stress cloud diagram of simultaneous detonation in double-hole model
据云图显示,在t<449.26s前,两炮孔产生的应力波相互独立,随着时间推移,应力波逐渐扩大,在t=749.48s时,应力波产生叠加,从数值条信息显示,在t=749.48s和t=1 049.80s时,两个炮孔水平连线处应力值分别为4.095×102MPa和2.092×102MPa,叠加处应力立刻衰减,并结合爆破漏斗原理[16],此处为最不利状态。此外两个炮孔中垂线处应力波传播的远近决定了爆破的范围,范围越大,炸药利用率越高,反之炸药利用率越小。当t=1 049.80s时,由云图形状可以判断,此时爆破范围最大,说明此时炸药利用率最高。
综合以上分析,选取4个位置单元进行数据提取,即两个炮孔间中垂线,第1炮孔水平线,第1炮孔中垂线以及第2炮孔中垂线。
2.2 应力数据
1)数据提取。在花岗岩中的不同位置分别设置监测单元,观察监测单元在整个爆破过程中所受应力的变化情况。从云图显示,两个炮孔间中垂线处出现应力叠加,应力变化最明显。以TNT炸药在孔距为380 cm时,两个炮孔间中垂线的6个单元数据为例进行分析。两个炮孔间中垂线所在直线处6个不同单元位置的爆破应力变化如图3所示,在6个单元位置处均出现拉应力或压应力,致使岩石击碎。2 ms前6个位置单元处均出现波峰最大值,此时岩石被击碎,随着时间推移,岩石被拉碎;8 ms后,应力变化逐渐减弱,趋于平缓。
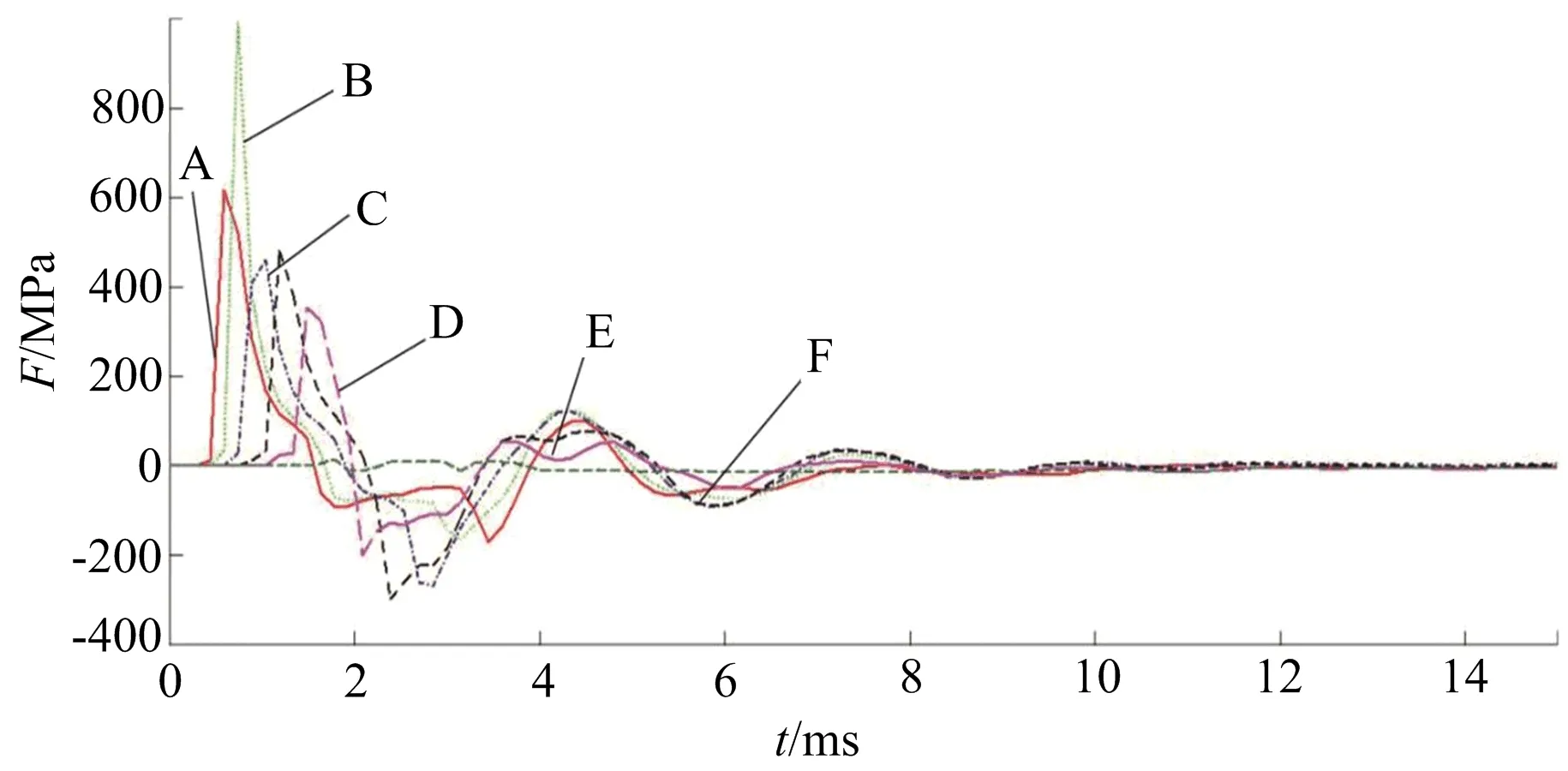
注:A~F的单元编号依次为1 854、58 815、56 605、54 395、52 185、50 400图3 爆破介质6个单元应力时程Fig.3 Six unit stress time history curve of blasting medium
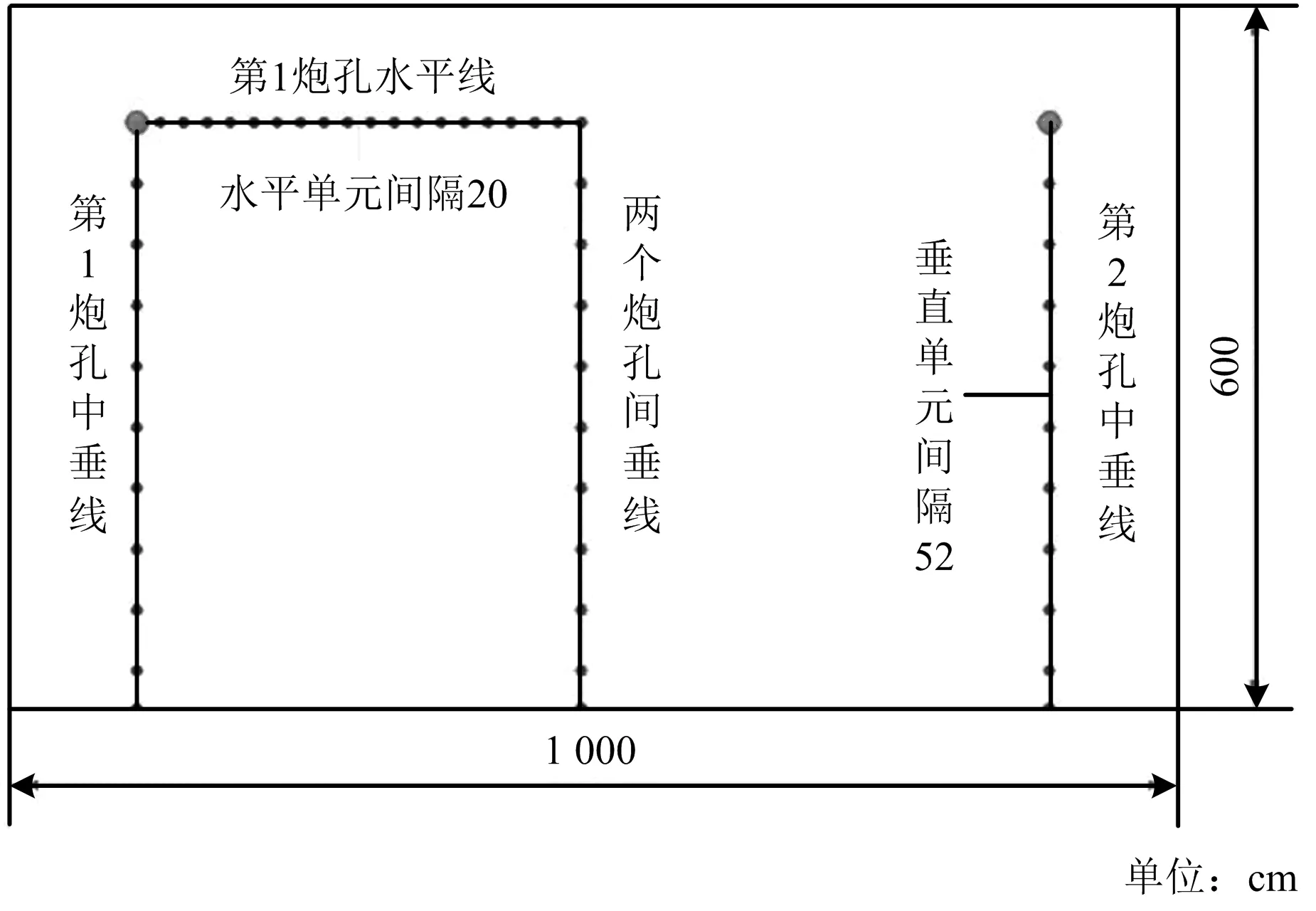
图4 模拟数据提取单元位置Fig.4 Simulation data extraction unit location
2)数据筛选及拟合。因为爆破过程中应力以波的形式传播,若波峰处的应力值超过岩石的抗压强度23.04 MPa或抗拉强度5.09 MPa时,岩石就会被均匀压碎或拉碎。筛选4个各单元点最大应力,进行应力时间指数函数拟合。
爆破速度极快,其以指数式函数递减,故存在同一时间点对应不同应力的情况。此时函数拟合时应遵循以下原则:必选应力波波峰值数据,剔除应力负值,中间数据根据指数函数递减性进行选择,同时保证拟合度R2>0.85。拟合函数表示爆破过程中不同时刻、不同位置单元所受应力的最大值。即F=cabt,F为应力,MPa;a、b、c为常数;t为时间,s。
3)数据计算。拟合函数为爆炸式指数函数式F=cabt=23.04 MPa,所求时间t为岩石可被击碎的结束时间点。由图3可知,应力波传递过程中,仅有部分时间点或时间段所对应的应力才能使位置单元处的岩石被击碎,即该段时间的总和为有效爆破时间。
有效爆破时间的提取方法:在两个炮孔间中垂线方向、距第1炮孔水平方向、第1炮孔中垂线方向和第2炮孔中垂线方向,分别提取使用不同炸药对花岗岩进行爆破时,爆破最深处位置单元的应力时程。在t时间内选择应力数据值大于23.04 MPa或小于-5.09 MPa的数据所对应的时间,对其进行时间累加求和,即为有效爆破时间。有效爆破时间与岩石击碎时间t的比值称为有效爆破时间百分比(%)。
由此可知,当岩石爆破深度的值越大,说明爆破范围越广,炸药的利用率越高;有效爆破时间百分比越大,岩石爆破块状越均匀,爆破效果越好,越有利于矿山开发。
2.3 数据整理
评定何种炸药对花岗岩的利用率高,主要考虑岩石的爆破范围,即深度d(cm);评定何种炸药对花岗岩的爆破效果最好,主要考虑爆破后岩石的铲状均匀度,即有效爆破时间百分比(%)。
10种炸药在不同位置单元的爆破深度如表3所示,有效爆破时间百分比如表4所示。
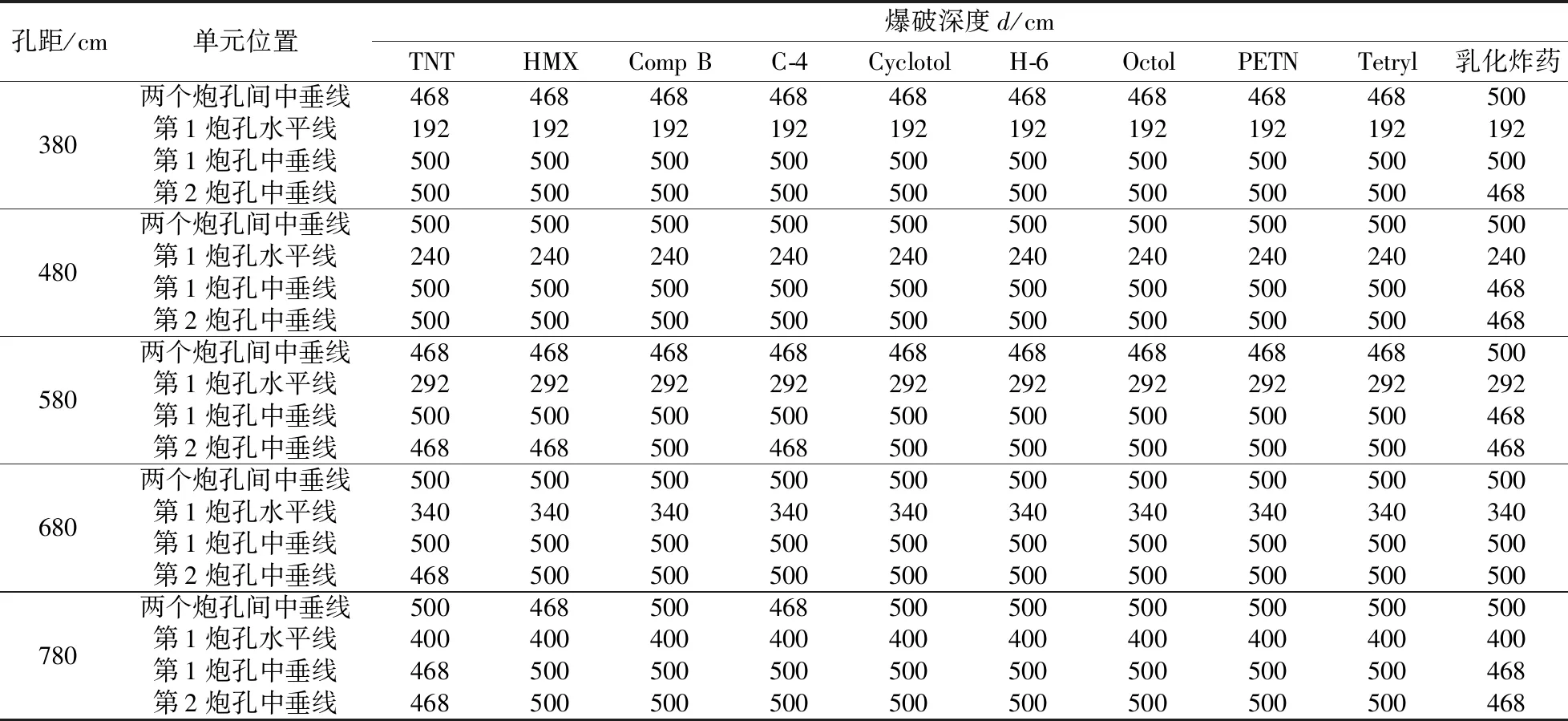
表3 不同炸药对花岗岩不同单元位置的爆破深度Table 3 Blasting depth of different explosives in different element positions of granite
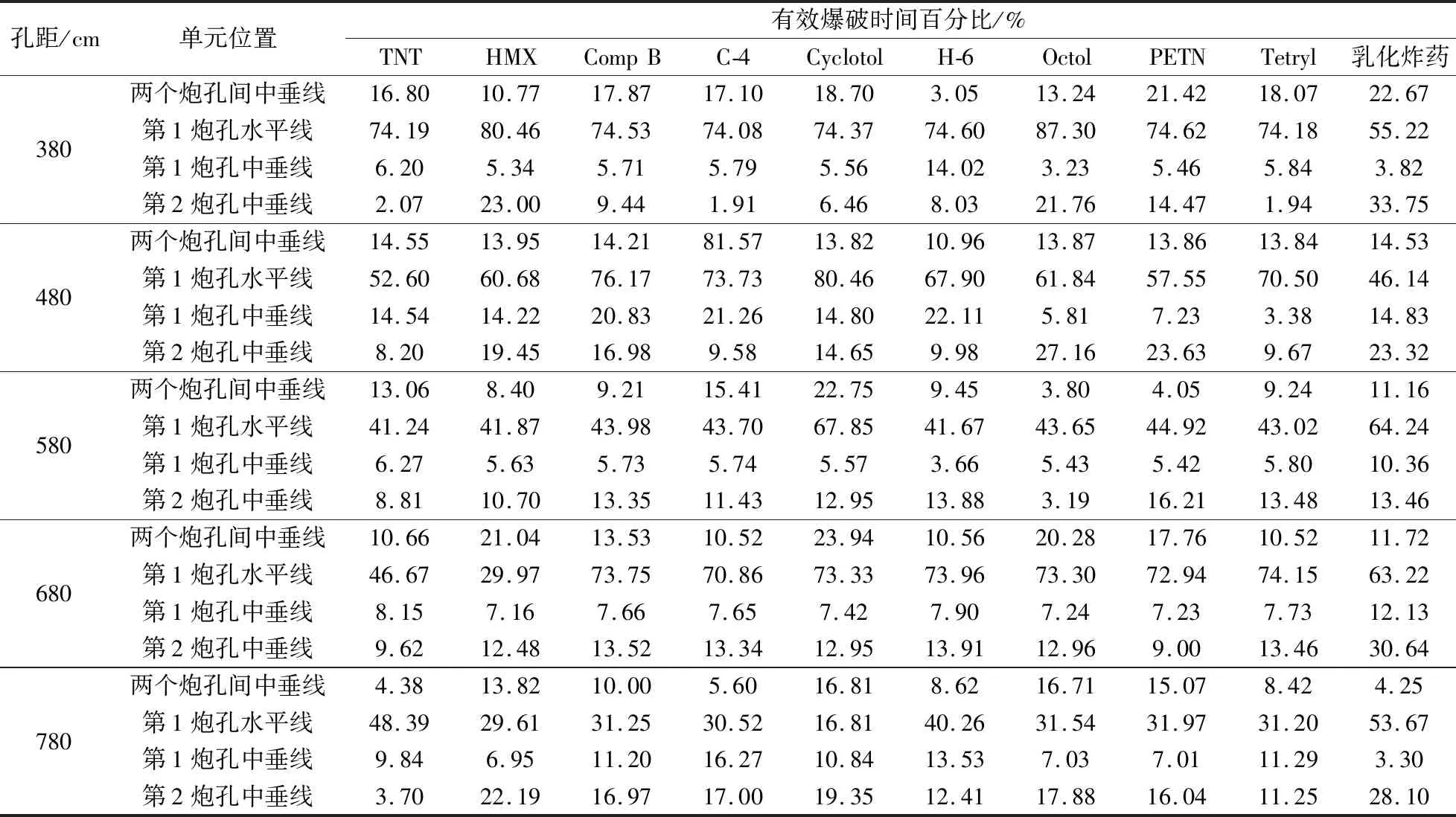
表4 不同炸药对花岗岩不同单元位置有效爆破时间百分比 Table 4 Percentage of effective blasting time of different explosives for different units of granite
3 数据分析
3.1 爆破深度与炸药利用率
从实际经验得出,单位体积炸药量与岩石匹配时,爆破深度的值越大,岩石被击碎的范围越大,说明炸药利用率越高。据表3数据显示,在两个炮孔间中垂线、第1炮孔水平线、第1炮孔中垂线和第2炮孔中垂线处的爆破深度分别为500、400、500、500 cm时炸药的利用率最大,此时共有6种炸药,分别是:Comp B、Cyclotol、H-6、Octol、PETN和Tetryl,此时炮孔间距为780 cm。对比而言,TNT炸药和乳化炸药在各单元位置爆破深度并不理想,炸药的利用率不及以上6种炸药。
3.2 有效爆破时间百分比与爆破效果
矿山爆破后,岩石的铲状将影响后期开采工作,爆破后岩石的块状不均匀或存在特大岩石块,将使后期开采难度增大,这说明爆破效果不好。在爆破深度分析的基础上,对孔距为780 cm时6种炸药的有效爆破时间百分比进行对比分析。据表4数据显示,Cyclotol炸药在两个炮孔间中垂线处有效爆破时间百分比最大,根据爆破漏斗原理,百分比较大,爆破效果越好。其次,Cyclotol炸药在第2炮孔中垂线处的有效爆破时间百分比均大于其他5种炸药,虽然H-6炸药在第1炮孔水平线、第1炮孔中垂线位置处的有效爆破时间百分比取得最大值40.26%和13.53%,但在孔距为780 cm的情况下,该炸药在最不利点处即两个炮孔间中垂线的有效爆破时间百分比低于Cyclotol炸药,说明Cyclotol炸药与花岗岩匹配时,岩石破碎后铲状更均匀,爆破效果最佳。
由波阻抗理论分析,凡炸药具有较大阻抗或者它的阻抗与岩石的阻抗越接近,炸药爆破时传给岩石的能量就多一些,而且在岩石中所引起的应变也要大一些[13],即ρmcm=ρece,其中ρm为岩石密度;ρe为炸药密度;cm为岩石纵波波速;ce为炸药纵波波速[17]。Cyclotol炸药波阻抗近似等于花岗岩波阻抗,符合波阻抗理论,与有效爆破时间百分比分析结果一致,再次说明花岗岩与Cyclotol炸药匹配效果更佳。
4 结论
1)当炮孔间距为780 cm时,通过对比得出在10种不同炸药中,Cyclotol炸药在4个不同位置单元的爆破深度分别为500、400、500、500 cm,得出Cyclotol 炸药与花岗岩匹配,爆破范围更广,效果最好。
2)当炮孔间距为780 cm时,通过对比得出在10种不同炸药中,Cyclotol炸药在4个不同位置单元的有效爆破时间百分比分别为:16.81%、16.81%、10.84%、19.35%,得出Cyclotol 炸药与花岗岩匹配的爆破效果最佳。打破了使用TNT炸药和乳化炸药的常规,为特定矿山岩种爆破提供更有利的参考。

