“初中物理图像专题复习”探讨

(江苏省南京外国语学校仙林分校,江苏 南京 210097)

1 引言

图像是指在直角坐标系中绘出两个相关物理量之间的函数关系图线，它不仅能直观、形象地反映两个相关物理量之间的关系，也能清晰反映用抽象数学解析式或文字无法表达或表达不清的物理状态、过程、变化趋势。在初中物理教学中，重点在于培养学生的读图和用图的能力，消除学生对物理图像的思维障碍，提高学生对物理问题的综合分析能力。

2 精心设问,认识图像

2.1 认识直线从一个小活动开始

师：图1是什么图像？

图1

生：正比例函数图像。

师：同学们一眼就能看出来，这也说明了图像的一大优点——直观。

师：图1能表示哪两个物理量间的关系？

师：老师提供了一些字母磁铁，可以吸在黑板上，请你选择合适的字母磁铁贴在坐标轴上。

学生选择磁铁贴在坐标轴上(如图2)。

图2

师：为什么说这些物理量之间存在正比例函数关系？

生：因为物体做匀速直线运动时S=vt，v保持不变。根据公式m=ρV，对于同一种物质而言，ρ不变。在公式G=mg中，g是一个常量。根据公式U=IR，对于一个定值电阻来说，R保持不变。这些和我们数学上学习的y=kx的函数形式类似。

2.2 认识折线从热学实验开始

师：图3可能是哪种物质经历了怎样的物理变化？

图3

生：可能是冰升温再熔化成水，水温度升高，再沸腾。

师：说得很完整，老师在图3中添上单位和数据，可以从图像中获得哪些信息？

生2：冰初温是-20℃，在B点开始熔化，熔化经历了3min，在第4分钟熔化结束，到第14min开始沸腾。

师：还有没有补充的？

生3：水的比热容大于冰的比热容。

师：你是怎么判断的？

生3：从开始加热到第1分钟结束，冰温度升高20℃，第4分钟到第5分钟水的温度升高低于20℃，都是加热1分钟，且用同一个酒精灯加热，Q相等，由Q=cmΔt，Q、m一定，Δt水<Δt冰，所以c水>c冰。

师：说得非常棒，思路很清晰。

设计意图：无论是新授课还是复习课，问题设置是一堂课的灵魂，一系列高质量的问题能激励学生主动思考，提高学生的思维能力，进而提高课堂效率。

在本环节，笔者改变设问角度，大大地提高了问题的思维含量。如在认识折线时，笔者隐藏了数据，先让学生根据图像回答可能是哪种物质经历了哪种变化，小小的改变让学生感到新鲜，也能激发学生思考的主动性。

3 通过例题分析提炼方法

例1:小明在探究“物质放热的多少与哪些因素有关”时,分别用质量均为0.5kg的甲、乙两种液体进行对比实验,并根据实验数据画出了如图4所示的图像。在实验中，甲、乙两种液体在相同时间内放出的热量相等，分析图4可以得出:甲、乙两种液体的比热容大小关系是c甲c乙(选填“>”“<”或“=”)，若乙液体的比热容为2.1×103J/(kg·℃)，则甲液体的比热容大小是J/(kg·℃)；甲液体在0-10min内放出的热量为J

图4

例2：如图5所示，小明在“探究下沉的物体是否受到浮力”实验中，根据数据绘制出图6，请问横坐标、纵坐标分别表示什么物理量？

图6

例2的延伸：根据图7中的信息可以直接获得哪些物理量？可以间接的算出哪些物理量？

图7

师：总结一下刚刚分析的两道题目，你认为解决图像题应注意哪些方面？

生：我会首先看看坐标轴分别表示什么物理量,再分析图线的走势，最后找出图像中重要的点。

师：看轴首当先，其次再看线，找点是关键。

师：你们认为有哪些点是需要找的?

生:如图4中的交点，当时间t=15min时，对应的温度分别为20℃、40℃,由此可比较甲、乙比热容的大小。还有图4的格点中，第10min对应的点不在图像方格上，我们找到第15min对应的点，算出15min放出的热量，进而可算出10min内放出的热量。

师：有没有补充的？

生：图6中的拐点也是我们要找的。

师：找点是关键，关键是找交点、格点、拐点。

设计意图：完成了两道典型例题的分析后，带领学生进行反思小结，归纳出图像题的一般解题思路：看轴首当先，其次再看线，找点是关键。

物理教学的根本不仅要学习知识，还要提高分析问题和解决问题的能力。为了实现这一目的，可以在探索思路的过程中进行，也可以在解题结束后加以提炼，让学生思考：在解题过程中运用了哪些方法？得到哪些有用的结论？引导他们反思、总结解图像问题的思路。

4 应用DIS呈现实验图像

师：你认为图8能表示哪两个物理量间的关系？

图8

生：能表示小灯泡的U和I的关系。

师：是不是呢？我们一起做一个实验。

教师简单介绍DIS(数字化实验系统)装置，利用DIS测量流经小灯泡的电流和两端电压，绘制出的图像如图9。

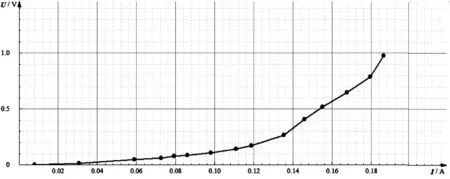
图9

师:请思考为什么曲线向上弯曲？

生：小灯泡的电阻随温度的升高而增大，U=IR，当电流在增大，电阻也在增大，因此电压增大得更多，因此曲线向上弯曲。

设计意图：本节课图像专题复习主线从直线到折线再到曲线，小灯泡的U-I图像是典型的曲线图像，本环节通过DIS实时采集数据，迅速将图像呈现在学生眼前，提高了复习效率。

5 前后联系，触类旁通

有一些题目尽管物理情境不同,但所涉及的知识点或解题方法是类似的,可以通过类比、归纳，用相同的知识或方法去解答这一类问题，学生以后碰到同类问题，能快速地复现解题思路。

师：如图10所示，曲线上有两点A、B，如何比较RA与RB的大小？

生1上讲台边画图边讲解(如图11)。

图10

图11

生1：将A、B两点与原点相连，再找第三个点C点，使IC=IA，此时UC>UA，所以RC>RA，又因为RB=RC，所以RB>RA。

师：如果我把这根曲线去掉，这个图大家熟悉吗？

教师出示图12，该图来自南京市2017年中考题，比较ρA与ρB的大小关系。

图12

师：此类题目都可以采用刚才同学讲解的方法，将图像中的两个点与原点相连，画横线或者竖线找到第三个点，先与第三个点比较，进而比较原来两点的关系。

设计意图：以上两例所用物理知识不同，分析方法相同，用一种方法去解决同种类型的一系列习题，可把学生从“题海”中解放出来，以后碰到类似的问题时，能举一反三，触类旁通。