基于EEMD的地铁隧道爆破振动信号分析与应用研究

韦 啸， 高文学， 王林台， 曹晓立

(北京工业大学建筑工程学院， 北京 100124)

0 引言

振动信号处理与分析是研究城市隧道掘进爆破振动效应的重要途径，也是爆破振动控制技术研究的有效依据。爆破振动信号是各种频率成分的混合体，包含了能反映场地特征和爆破特征的重要信息，通常体现在振动幅值、频率以及能量分布特征上。因此，对振动信号进行处理与分析，从而提取准确的爆破振动特征信息是进行城市隧道掘进爆破振动效应研究的重要环节。

国内外已有学者在振动信号方面做了相关的研究。张雪亮等[1]结合已有研究成果，指出爆破振动信号具有典型的非平稳特性，加之在不同工程背景下传播介质的复杂性，传统的傅里叶变换等信号分析方法无法满足研究要求。Huang等[2]提出了EMD方法，其Hilbert-Huang分析方法近年来得到广泛的应用[3-6]，但仍然存在着缺点，其分解得到的各阶IMF(intrinsic mode function，固有模态函数)分量之间可能会存在模态混叠现象，容易造成去噪后的信号失真。针对这种情况，文献[7-8]提出了EEMD方法，该方法具有良好自适应性的特点，同时可以有效地改善信号分解的去噪效果。张树标等[9]利用EEMD方法，对某爆破振动信号进行了去噪处理，结果表明EEMD方法自适应性较好，能充分保留信号本身固有的非平稳特性。赵明生等[10]对某爆破振动信号进行了EEMD和小波去噪，结果表明小波法去噪较依赖小波基函数的选取，未能摆脱傅里叶变换带来的缺陷； 而EEMD方法更加灵活、方便，去噪效果较好。综上所述，EEMD方法具有良好的自适应性，去噪效果显著，而目前城市地铁隧道掘进爆破领域采用的EMD方法会造成模态混叠，进而导致分析结果不准确，故EEMD方法在该方面的应用研究具有一定的实际意义。

为了分析城市隧道掘进爆破振动信号的特征信息，从而研究城市隧道掘进爆破振动效应，本文基于乌鲁木齐轨道交通1号线掘进爆破振动监测数据，采用基于EEMD和EMD的去噪方法分别对爆破振动信号进行处理，利用信噪比法与均值误差法进行量化评估，将2种方法进行对比分析，以选择更加合理的去噪方法。对去噪后的爆破振动信号的时频特征和能量分布特征进行分析，提出城市地铁隧道爆破振动控制技术，以期为城市地铁隧道爆破开挖稳定性研究和对临近建(构)筑物的安全控制提供借鉴。

1 EEMD原理

EMD分解过程中需要构造信号的极值点的上下包络线并求其均值曲线，当信号时频特征存在异常值时，必然影响极值点选取，使得包络线产生失真，从而经过分解得到的IMF分量出现模态混叠现象，会降低信号去噪的效果。针对这种情况，发展了EEMD方法，即原信号在加入白噪声后，再经过经验模态分解，得到一系列代表了信号特征的不同时间尺度的固有模态函数。EEMD分解步骤如下。

1)将不同的高斯白噪声附加到原信号中，

xi(t)=x(t)+wi(t)。

(1)

式中i=1, 2, …,I，为总体集成白噪声次数。

(2)

式中：cik(t)(k=1,2, …,n)为IMF模态分量，表示xi(t)在不同频率段从高到低的成分分量；rn(t)为余量，代表信号的趋势项。

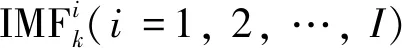
(3)

当k足够大时，即使用足够多的全体均值时，噪声将相互抵消至可忽略的程度，得到的均值结果可视为最终的IMF分量。上述IMFk可视为经EEMD运算后的第k阶IMF分量ck(t)。

对分解后的分量进行HHT变换分析，研究爆破振动信号的时频特性和能量在时域、频域中的分布规律。

2 工程实例分析

乌鲁木齐轨道交通1号线右线隧道中营工站和小西沟站区间位于里程桩号 YDK13 + 462.542～YDK14+727.612。地表下伏于杂填土，层厚8～15 m。以砂岩、灰岩为主，粒径组成： 2～20 mm约55%，20～60 mm约10%，大于60 mm约10%，其余以杂砂砾充填。隧道上覆岩石多为中风化砂岩，围岩级别为V级，采用钻爆法施工。

该区段隧道沿线下穿人行天桥、BRT(快速公交)车站以及高架桥建筑物，隧道拱顶距离管线底垂直距离为8.6～11.2 m； 其中1号施工竖井位于某建筑红线外空地内，临近污水管线，且横通道需下穿该管线； 2号施工竖井距离第四十五中学教学楼45 m，临近中学操场。该段施工重点控制爆破振动对地表及周边建(构)筑物的影响。

2.1 地铁隧道爆破设计参数

基于隧道施工环境及围岩地质条件，该区段地铁隧道采用上下台阶法施工。合理选取爆破参数，以控制爆破振动对围岩和混凝土套拱结构的影响。上台阶炮孔布置如图1所示，各段位药量如表1所示。

图1 上台阶炮孔布置图(单位： mm)

2.2 爆破振动监测方案

爆破振动监测位于地铁隧道桩号YDK14+334.05～+372.05，研究重点为监测隧道上台阶爆破开挖时，已成洞区地表的爆破振动信号。考虑到空洞效应[11]的影响，以隧道掌子面为对称点，到掌子面距离相同的后方已成洞区上方测点地表爆破振动速度峰值要略大于掌子面前方未成洞区上方地表测点爆破振动速度峰值，故对已成洞区地表进行振动监测，并选取已成洞区振动速度峰值最大的测点数据进行分析，以研究隧道掘进爆破引起的振动对隧道已成洞区上方地表建(构)筑物的影响，并提出合理的爆破振动控制措施。监测点所在地表距隧道拱顶9.90 m，监测点1—8

号置于掌子面后方已成洞区地表，且监测点布置在隧道中心线上。仪器采样率为8 000 Hz，1号测点距离掌子面上方地表5 m，测点间相距为5 m，监测点布置如图2所示。

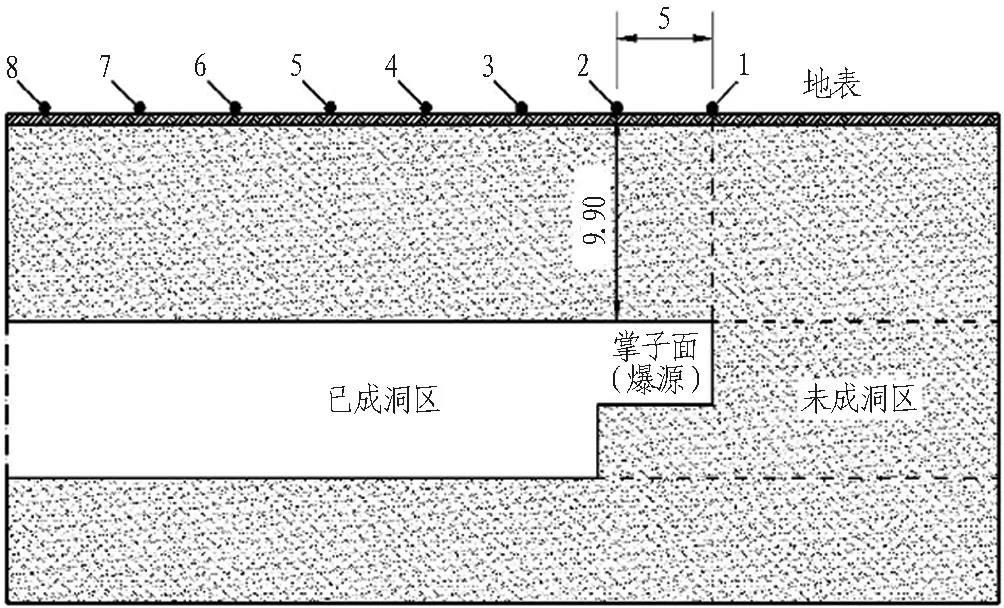
图2 测点布置图(单位： m)

通过振动监测，得到地表各测点垂直方向振动速度最大值，如表2所示。对监测点振速峰值进行回归拟合，得到振速回归公式：

(4)

根据回归公式(4)计算各测点振速值，并与监测值进行对比，结果如表2所示。

表1 上台阶各段炮孔装药量

表2监测值与拟合值对比

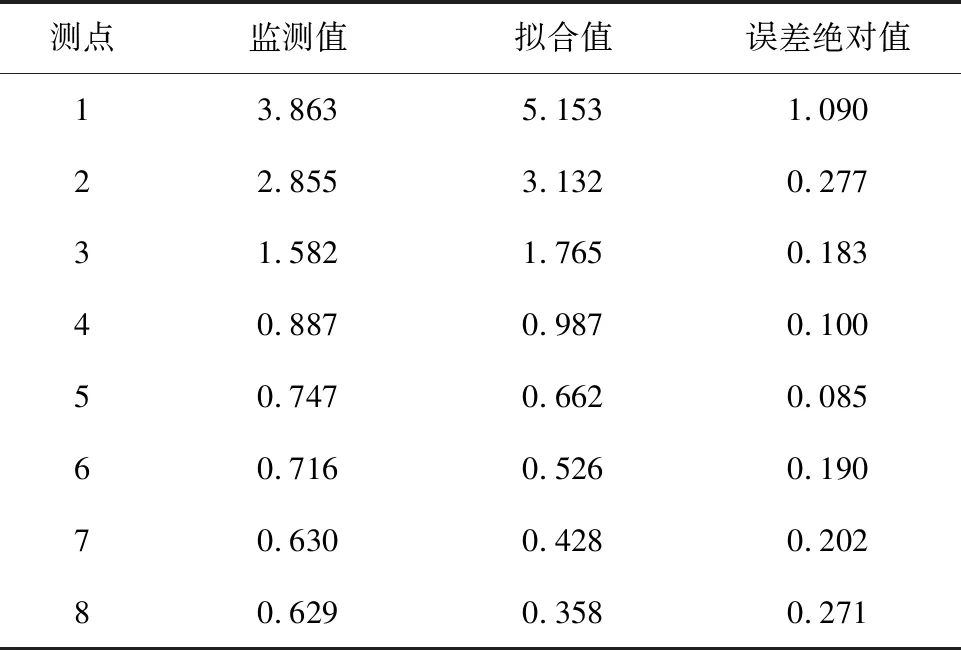
Table 2 Comparison between monitoring values and fitted values cm/s

由表2可知，1号测点监测值较拟合值误差较大，原因是相同爆破条件下，一般土壤介质中爆破振动速度比坚硬岩石中要小，这是由于不同传播介质对爆破振动波的传播有不同的影响[12]。乌鲁木齐地铁隧道上覆围岩为杂填土，较为软弱破碎，围岩级别为V级，故隧道掘进爆破引起的地表振动速度偏小。

基于所得回归公式对掌子面正上方测点振速进行修正，以拟合振速峰值5.153 cm/s作为掌子面正上方1号测点振速峰值。各测点振动速度峰值如图3所示。

由图3可知： 掌子面正上方的1号测点振动速度最大，2—8号监测点处垂直方向的振动速度峰值随着各监测点距掌子面距离的增大而衰减；距离掌子面距离较近的1—3号测点振速衰减较快，距离掌子面距离较远的4—8号测点振速衰减较慢。

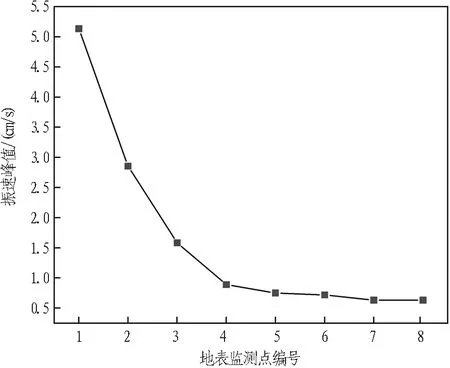
图3 各监测点处垂直方向振动速度峰值

选取已成洞区振动速度峰值最大的监测点数据进行分析。此外，离2号测点不远处有人行天桥阶梯，路两侧建有学校和商场，为钢筋混凝土框架结构建筑，应考虑爆破振动对其造成的影响，故选取2号监测点的爆破振动信号进行分析。2号监测点所处地表的垂直方向的爆破振动信号曲线如图4所示，图中振速峰值出现在0.05 s，最大垂直振速为2.85 cm/s。

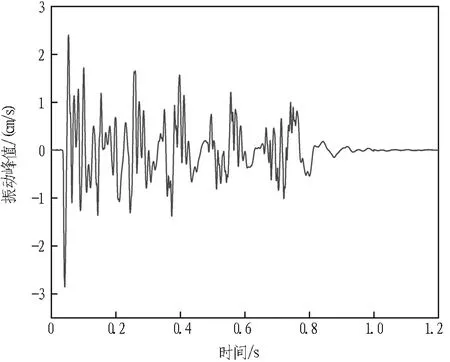
图4 2号监测点爆破振动信号图

3 爆破振动信号去噪处理与评价

3.1 爆破振动信号去噪

对2号监测点爆破振动信号分别进行EMD处理和EMMD处理。对爆破振动信号进行EMD处理后得到10个IMF分量和1个残余分量，如图5所示。在图5中，代表着信号高频成分的IMF分量c1存在着信号突变，去噪时应当去除；c2—c4时间尺度区分不明显，存在模态混叠，这对爆破振动信号的能量及频谱分析是不利的。

(a) c1

(b) c2

(c) c3

(d) c4

(e) c5

(f) c6

(g) c7

(h) c8

(i) c9

(j) c10

(k) 残留余项r

针对上述情况，运用EEMD对其进行优化。其中EEMD的预设参数为： 总体白噪声集成次数i=100，白噪声标准差为0.1。运用EEMD去噪法对爆破振动信号进行处理后得到12个IMF分量和1个残余分量，如图6所示。各个分量ci之间时间尺度区分较为明显，说明EEMD解决了EMD模态混叠的缺陷并保留了自适应性。其中，c1和c2为信号高频成分，且频率沿时间轴基本不发生衰减，其幅值很小，包含的能量占总能量的比值最小，可视为信号噪声，应当去除。通过EMD法和EEMD法分别对原始信号进行分解，筛选出高频噪声并将其去除，将去噪后的IMF分量分别经由Matlab编程重组，将得到的结果进行量化评价。

(a) c1

(b) c2

(c) c3

(d) c4

(e) c5

(f) c6

(g) c7

(h) c8

(i) c9 (j) c10

(k) c11

(l) c12

(m) 残留余项r

3.2 爆破振动信号去噪评价

基于EMD和EEMD分解结果，去除噪声分量并进行重组，对去噪后的振动信号进行量化评价。

3.2.1 SNR方法

利用SNR方法对上述2种方法得到的去噪信号进行量化评价。SNR是指检测信号中有用信号和噪声信号的比值，其值越大代表去噪效果越好[13]。其定义可用下式表示：

(5)

式中：x(t)为原始爆破振动信号；x(t)′为去噪后的信号。

SNR计算值见表3。由表3量化评价结果可知： EEMD方法得出的结果信噪比更高，其去噪效果更好。

表3 信噪比计算值

3.2.2 均方根误差(RMSE)量化评价

均方根误差又叫标准误差，它是对所测量数据的可靠性进行衡量，是信号数据精确度的参数，所以标准误差越小，说明测量数据的可靠性越大，相反，则可靠性越小。其定义可用下式表示：

(6)

式(6)中k值表示信号的长度，用原始爆破振动信号与去噪后的信号做方差运算再开平方，计算所得到的参数值越小，则证明去噪的效果越显著。这种算法依据的原理，如下式所示：

(7)

式中：x(k)为原始爆破振动信号；x(t)′为去噪后的信号。

计算后得出的误差值见表4。

表4 均方根误差计算值

由表4量化评价结果可知： 均方根误差更小，并且信噪比更高。结合EMD和EEMD的分解结果，可知由EMD方法得到的信号高频成分存在信号突变，不同分量之间存在模态混叠；由EEMD方法得到的信号高频成分其频率沿时间轴基本不发生衰减，且幅值很小，具有典型的噪声特征，不同信号分量之间区别明显，未造成模态混叠，因此EEMD方法去噪效果更显著。根据以上描述，选取EEMD方法对爆破振动信号进行去噪处理。

4 爆破振动信号分析

对经由EEMD方法去噪后的振动信号进行EEMD分解，将每个IMF分量所包含的能量通过柱状图表达，如图7所示。

结合图6与图7进行分析：c4—c8分量幅值较大，占有了爆破振动信号的大部分能量，是影响地表及临近建(构)筑物安全的主要部分，其后的IMF分量随着频率的减小，波长在变大，直至最后得到的残留余量r。

对分解后的信号进行HHT，得Hilbert灰度能量谱图，如图8所示。图8直观地表现了振动信号的时间、频率、能量的关系。从图8中可以看出，在当前起爆方式下，爆破振动信号的能量基本分布在频率段5～80 Hz，并且主要分布在5～50 Hz以下的低频段，这与EEMD的结果吻合。在厚度大于2～3 m的土壤介质中，频率范围一般为1～20 Hz，在岩石介质中，频率范围一般为1～100 Hz[12]，故所得结果在合理的范围内。根据《爆破安全规程》[14]规定的安全允许振速标准，一般商用、民用建筑的安全允许振速根据振动频率划分为不同标准，当振动频率大于50 Hz时，振速应小于3.0 cm/s，当振动频率小于50 Hz时，振速应小于2.5 cm/s。考虑测点附近存在的人行天桥及钢筋混凝土框架结构建筑，结合现场实测值，可知离掌子面较近处测点振速略大于安全允许值，较远处测点实测值满足规范要求。此外，一般地面建(构)筑物的自振频率在10 Hz左右，因此该频段的振动信号成分最有可能引发临近建(构)筑物产生共振而产生破坏，所以应采取合理的降震增频措施[15-18]来减小振动对建(构)筑物的影响。

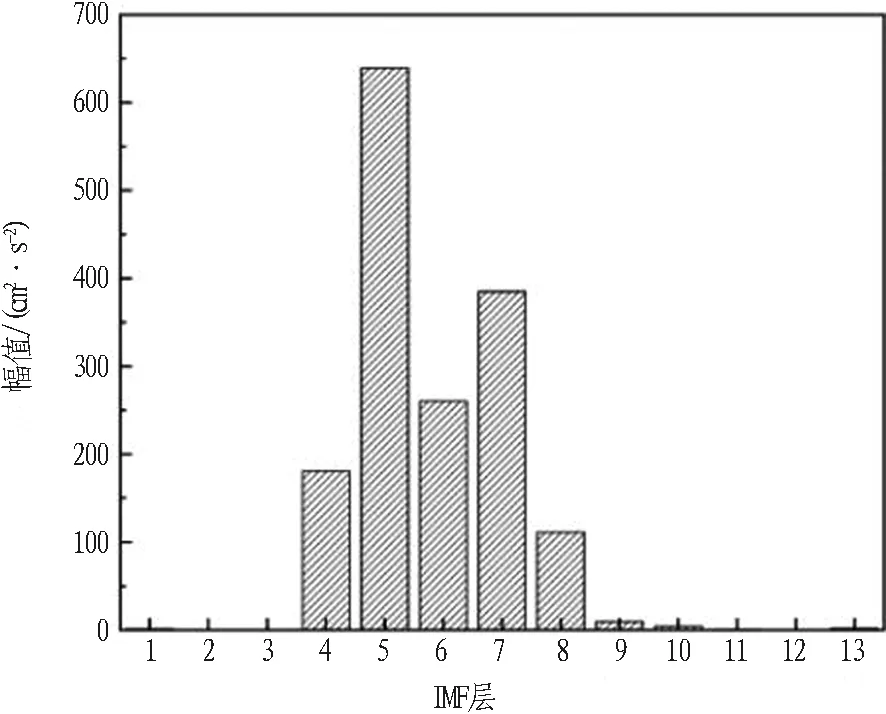
图7 IMF所含能量分布图

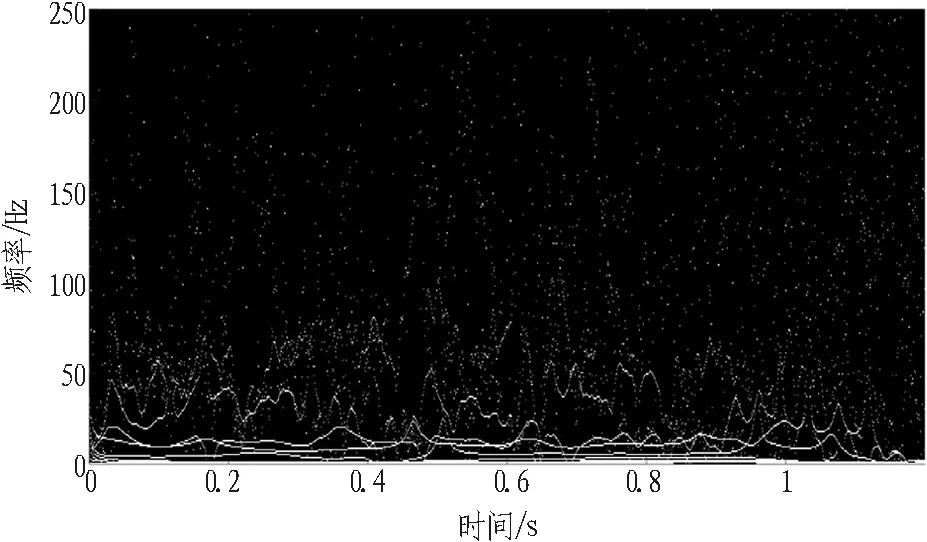
图8 Hilbert灰度能量谱图

为了考察振动信号能量分布与时间的关系，对数据进行进一步处理可得到瞬时能量谱，如图9所示。从图9中可知，爆破振动瞬时能量在不同采样点出现了多个峰值，这是由于不同段位炮孔起爆的时间差引起的； 其中，最大值为11.09 cm2/s2，对应时刻为0.05 s处，与爆破振速最大值所在的时刻一致，为掏槽孔爆破的时刻，说明了掏槽孔爆破由于岩石的夹制作用而产生的能量较大，可采取减震掏槽爆破技术控制掏槽爆破振动，例如增大掏槽爆破与目标物距离、改善掏槽结构形式等方法。

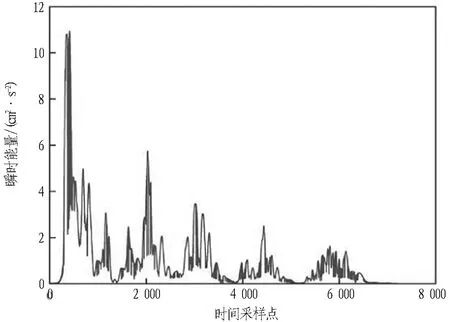
图9 瞬时能量分布图

为了考察振动能量分布与频率的关系，对时频数据进一步处理可得到信号的边际能量谱，如图10所示，可直观地反映能量在频域上的分布情况。从图10中可以看出，边际能量谱最大值为333.0 cm2/s，对应频率为50 Hz，能量集中在5～80 Hz，其中频率5～50 Hz是能量分布的主要区间。

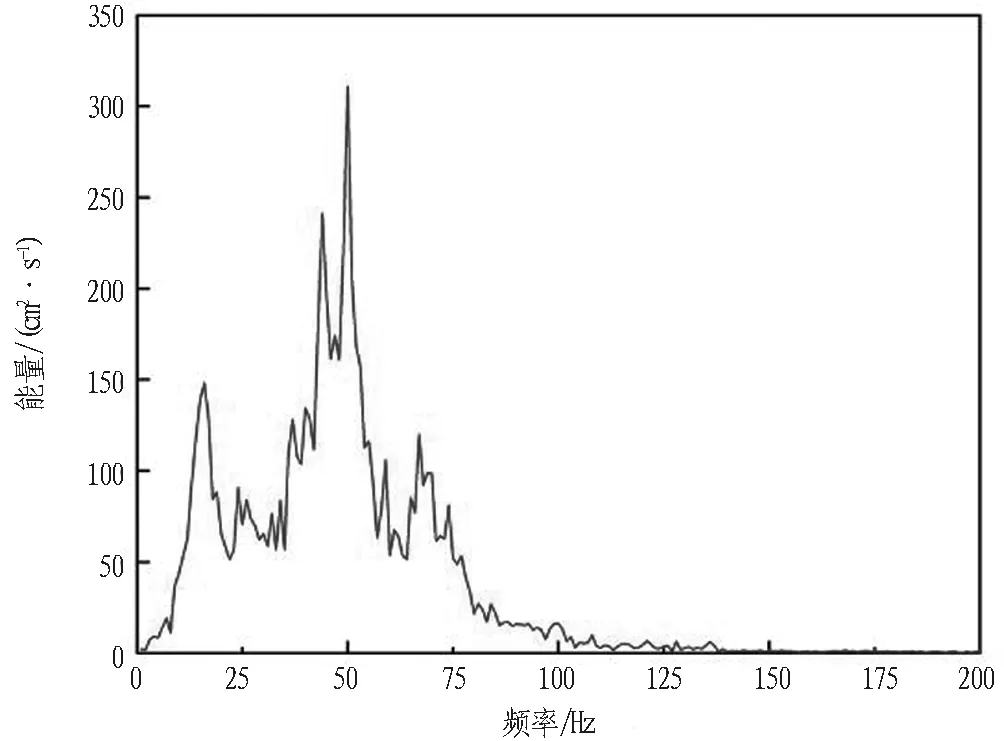
图10 爆破振动信号边际能量谱图

5 地铁隧道爆破振动控制技术

地铁隧道掘进爆破，应关注爆破振动对建(构)筑物的影响。基于上述爆破振动信号分析的结论，提出以下关于地铁隧道掘进爆破的控制技术措施。

1)减震掏槽爆破。振动监测结果表明，在掏槽孔单响药量和辅助孔单响药量相差不大的情况下，掏槽孔爆破引起的振动显著增强。为此，可采用多级楔形掏槽结构形式，降低岩石的夹制作用，分散最大单段药量来控制爆破振动，同时循环进尺因爆破效果改善而得到提高。此外，合理布置掏槽位置，上台阶掏槽孔应尽量布置在开挖部位的底部，以加大掏槽部位至地表的距离，减小掏槽爆破对地表建(构)筑物的影响。

2)毫秒延期起爆减震。采用毫秒延期起爆网路，选取合理的延期时间，可有效控制单段起爆最大药量，降低振动强度，提高振动频率。此外，采用混合复杂起爆网路，可有效提高振动频率，有较好的破碎效果。

3)采用水压爆破和预裂隔震爆破等特殊的爆破形式。水压爆破下，爆炸能量没有损失地经过水传递到炮孔围岩中，有利于围岩破碎，可降低炸药单耗。采用预裂隔震爆破，预裂爆破形成的贯通裂缝对应力波起到阻断作用，起到了良好的隔震效果；此外，预裂爆破不耦合装药的降压作用，可有效降低爆破振动。

6 结论与建议

采用基于EEMD的HHT方法对乌鲁木齐轨道交通1号线开挖爆破振动信号进行了处理和分析，得到以下结论：

1)EEMD法去噪结果信噪比和均方根误差值分别为30.51和0.005 5； EMD法去噪结果信噪比和误差值分别为20.88和0.010，去噪后的信号信噪比更高。经比较，EEMD去噪法要优于EMD去噪法，有用信息保留更完备，得到的IMF分量具有明确的物理意义。

2)在当前起爆方式下，爆破振动能量基本由5～80 Hz频率段内的信号成分的能量组成，并且主要分布在50 Hz以下的低频段。根据《爆破安全规程》规定的安全允许振速标准，周边建(构)筑物的安全允许振速值为2.5 cm/s； 结合现场实测值，离掌子面较近处测点振速略大于安全允许振速值，较远处测点实测值满足标准要求。为了减小爆破振动对周边建(构)筑物的影响，可采用合适的降震增频技术，例如毫秒延期起爆网路及混合复杂起爆网路，来降低振动强度，提高爆破振动频率。

3)由于不同段位炮孔起爆的时间差，爆破振动瞬时能量在不同采样点出现了多个峰值，且与振动速度峰值所在的时刻一致，说明瞬时能量谱能较好地体现爆破过程中振动效应随时间的变化规律。

本文基于监测数据，应用EEMD方法对振动信号进行去噪与分析，研究爆破振动信号的时频特征和能量分布特征。下一步，可结合数值模拟、振动信号分析等，深化研究爆破振动信号的相关特征，从而探讨城市地铁隧道掘进爆破带来的振动影响。