全自动草莓钵苗移栽机构优化设计与试验
许春林 吕志军 辛 亮
(东北农业大学工程学院, 哈尔滨 150030)
0 引言
草莓是经济价值较高的小浆果,具有易繁殖、生长周期短、管理方便等优点[1-2],其主要的种植方式是将生长在草莓匍匐茎繁殖形成的子株直接移栽到田中[3]。而将子株栽植到带有营养土的钵盘中进行育秧,不仅能大幅提高移栽子株的成活率,使其根系更发达、苗更壮,而且有利于实现机械化移栽,提高作业效率[4]。
目前,我国已成为世界上最大的草莓生产国,但大多仍采用手工移栽的方式,国内外市场上未见针对草莓的全自动移栽装备[5]。草莓钵苗与旱田作物秧苗移栽要求相近,移栽机构是旱田移栽的关键工作部件。欧美国家全自动移栽机多采用机、电、液一体化技术,由单片机、电磁阀、气缸和机械手等装置分别完成取苗、输送和栽植等动作,价格昂贵,没有在国内得到推广[6];日本井关公司开发的全自动钵苗移栽机,其核心机构由取苗和植苗两套机构组合而成,分别用滑道传动完成取苗动作,用鸭嘴式栽植器完成栽植动作,结构复杂、效率低[7-8]。国内移栽机仍处于起步阶段,市场上主要是半自动移栽机,劳动强度大,漏苗率高,作业效率低[9-11]。国内科研单位针对蔬菜、花卉等移栽机构也展开了研究,包括应用于温室等的系列穴盘苗末端执行器的开发[12-13];俞高红等[14-15]提出了一种旋转式穴盘苗取苗机构和行星轮系蔬菜钵苗栽植机构,用回转体完成取苗动作,通过栽植机构将钵苗植入土中。
为了实现草莓钵苗的取栽一体化全自动移栽,本文提出一种采用一套回转机构实现草莓钵苗移栽的取苗、输送、挖穴和栽植4道工序的移栽机构。以Hermite插值法构建新型非圆齿轮[16-18],利用非圆齿轮传动分别实现“鹰嘴形”相对运动取苗轨迹[19]和配合凸轮滑道机构的挖穴轨迹;基于理论分析与建模,开发辅助分析优化设计软件,对全自动草莓钵苗移栽机构进行优化,以得到满足草莓移栽要求的运动轨迹和姿态。
1 移栽机构设计要求与工作原理
1.1 机构设计要求
草莓钵苗移栽是将匍匐茎子株移植到营养盘中育秧后移栽钵苗的过程,而草莓具有弓背朝向固定方向生长的特性,因此,为了便于草莓后期的移栽、生长、采收和管理,首先要求子株需在钵盘中朝同一方向进行育秧[20]。
育秧后的草莓钵苗如图1所示,其形态特征为茎叶分散、茎脆嫩易断、根系发达,易成良好的基质与根系结合体[2-3]。因此,移栽机构采用夹片扎入土钵中夹取的方式从钵盘中取秧,拔取土钵段轨迹长度要足够长,转角要小,保证土钵完全脱离钵盘过程不损伤土钵及根须,即满足夹土钵式的“鹰嘴形”取苗轨迹;然后夹持钵苗运输到栽植部位,栽植机构配合挖穴机构将钵苗强制推秧至挖好的穴孔内,栽植深度实现上不埋心、下不露根的定植深度原则[1],栽植后不推倒已栽好的秧苗,回程后完成一次移栽。

图1 草莓钵盘育苗根系盘根效果图Fig.1 Root packing effect diagram of strawberry seedlings
为了提高移栽效率,要求采用回转机构一次性完成全部取苗、输送、挖穴、栽植4个工序,回转一周完成两次移栽,且以上过程均不发生任何干涉。
1.2 机构工作原理
移栽机构是草莓移栽机的核心工作部件,该机构由两部分组成:非圆齿轮行星轮系传动与栽植臂部件组成的取苗栽植机构,见图2a;固定在匀速转动行星架上的凸轮配合非匀速运动栽植臂部件中杆机构组成的挖穴机构,见图2b。
两机构共同配合运转并分别在相应时刻完成取苗、输送、挖穴和栽植4道移栽工序。由于双臂机构的上、下取苗栽植机构和上、下挖穴机构布置在中心轴的两侧,运动轨迹和姿态相同,所以只对单侧移栽机构进行分析。
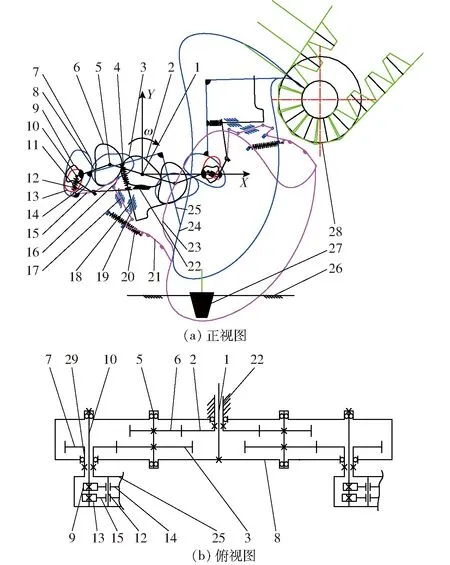
图2 草莓钵苗移栽机构结构示意图Fig.2 Schematics of strawberry potted seedling transplanting mechanism1.动力输入轴 2.太阳轮 3.中间轮B 4.推秧弹簧 5.中间轴 6.中间轮A 7.行星轮 8.行星架 9.推秧凸轮 10.凸轮轴 11.拨叉拉簧 12.拨叉轴 13.挖穴凸轮 14.推秧拨叉 15.挖穴拨叉 16.连杆A 17.连杆B 18.推秧杆 19.连杆C 20.挖穴铲拉簧 21.挖穴铲 22.机架 23.挖穴相对运动轨迹24.“鹰嘴形”相对运动取苗轨迹 25.栽植臂部件 26.地面 27.钵苗 28.秧箱 29.行星轴
为了满足移栽机构复杂轨迹的设计要求,需提高非圆齿轮节曲线和中心距的调节范围。因此,本机构非圆齿轮传动采用二级传动,太阳轮和中间轮A为一级传动,中间轮B和行星轮为二级传动,分别对应的两个齿轮节曲线参数一致[21-22]。相互啮合的齿轮均满足主动轮转一周从动轮也转一周,总传动比为1[23-25]。
取苗栽植机构工作原理:动力输入轴驱动行星架顺时针转动,在固定于机架的太阳轮的配合下,通过中间轮A和中间轴驱动中间轮B相对行星架做顺时针方向的自转,使行星轮及行星轴驱动栽植臂部件相对行星架做逆时针方向不等速运动,形成满足移栽要求的夹土钵取苗的“鹰嘴形”相对运动轨迹;栽植臂部件内的推秧凸轮与推秧拨叉作用,在推秧弹簧作用下,使推秧杆直线往复运动,控制秧针在相应位置完成闭合夹苗与张开推秧动作。
挖穴机构工作原理:挖穴凸轮随行星架做顺时针匀速转动,与栽植臂部件中挖穴拨叉的非匀速运动形成相对运动,从而挖穴拨叉依次通过连杆机构驱动挖穴铲摆动形成满足挖穴要求的相对运动作业轨迹。
通过两套机构不同时刻的配合,实现双臂机构互不干涉,同时作业过程中的取苗和运输阶段挖穴机构远离秧箱与栽植臂,防止发生干涉;在栽植钵苗时,挖穴机构在田中进行挖穴,随后栽植臂部件配合挖穴机构且不发生干涉地控制推秧装置进行推秧,准确可靠地将钵苗栽植到所挖的穴孔中,完成栽植,回程准备下一次作业,机构旋转一周完成两次移栽过程。
1.3 机构轨迹和姿态分析
保证全自动草莓钵苗移栽机构取苗栽植和挖穴质量的关键和难点是移栽和挖穴轨迹与姿态的优化设计,包括取苗栽植机构和挖穴机构各时刻的配合以及双臂作业整个过程互不干涉等,因此对移栽各关键时刻的轨迹和姿态进行分析:通过分析模拟人工取苗、栽植和挖穴动作,可知取苗、挖穴和栽植依次完成,精准配合,并要保证所挖穴口与所取钵苗一一对应。秧针取苗近似直线的进出轨迹是成功的关键,因此栽植臂形成的是“鹰嘴形”轨迹,如图3a所示。机构顺时针方向旋转,秧针在A点开始进入钵土并开始逐渐夹紧,到达B点后完全夹紧土钵,在AB段秧针沿着垂直钵盘方向且近似直线插入钵土中,之后开始取出钵苗,通过C点时处于被夹持状态的土钵完全脱离钵盘,BC段长度应大于钵土的深度,CD段是秧苗的输送阶段,秧针一直处于夹持钵土的状态,输送阶段钵土不与秧箱干涉,移栽机构在D点处完成推苗动作,实现钵苗的栽植过程,在DEA段,秧针处于张开状态,栽植臂准备下一周期的取苗和栽植作业。在FG段,挖穴铲处于工作阶段,能够满足穴口深度、长度和宽度要求,在GHF段,挖穴铲处于非工作阶段,挖穴铲准备下一周期的挖穴作业,此阶段主要是避免移栽机构其他部件的干涉。

图3 移栽机构运动轨迹Fig.3 Motion trajectories of transplanting mechanism1.取苗轨迹 2.挖穴轨迹
移栽机构工作状态下形成的绝对运动轨迹如图3b所示。
2 移栽机构运动学模型建立
2.1 基于Hermite插值成型的非圆齿轮节曲线
非圆齿轮节曲线的选择是非圆齿轮设计的关键,相较于偏心、椭圆和卵形等非圆齿轮,本文运用Hermite插值方法成型的非圆齿轮节曲线,可提高非圆齿轮的调节范围,满足移栽和挖穴特定、复杂的轨迹要求。Hermite插值多项式不仅要求所插入点上的函数值相等,而且对应的导数也相等,因此成型的曲线过渡更光滑[18]。
Hermite插值多项式为
(1)
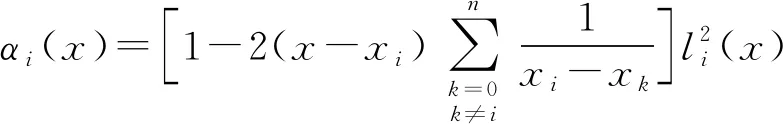
(2)
(3)
(4)
式中 (xi,f(xi))——插值点坐标
f′(xi)——插值点导数
αi(x)、λi(x)——Hermite插值基函数
li(x)——Lagrange插值基函数
由Hermite插值多项式可知,在极坐标系中分别给出n+1个满足要求的插值点的极角φn、极径rn和导数dn,可以推导出满足要求的节曲线方程
(5)
通过实际调试可得插值点数n+1=5时,满足移栽的节曲线要求,n+1<5时节曲线调节范围不满足要求,n+1>5时会出现节曲线突变的Runge现象;当首尾插值点重合时,保证节曲线的封闭性。由2n+1=2×4+1=9,可知所求节曲线方程为9次Hermite插值多项式[18]。
2.2 机构运动学分析
以太阳轮的转动中心O1为坐标原点,水平方向为X轴,垂直方向为Y轴建立坐标系,分别建立取苗栽植机构和挖穴机构运动学理论模型。以单侧栽植臂和挖穴机构为研究对象[21],另一侧为行星架转过180°后的位置。
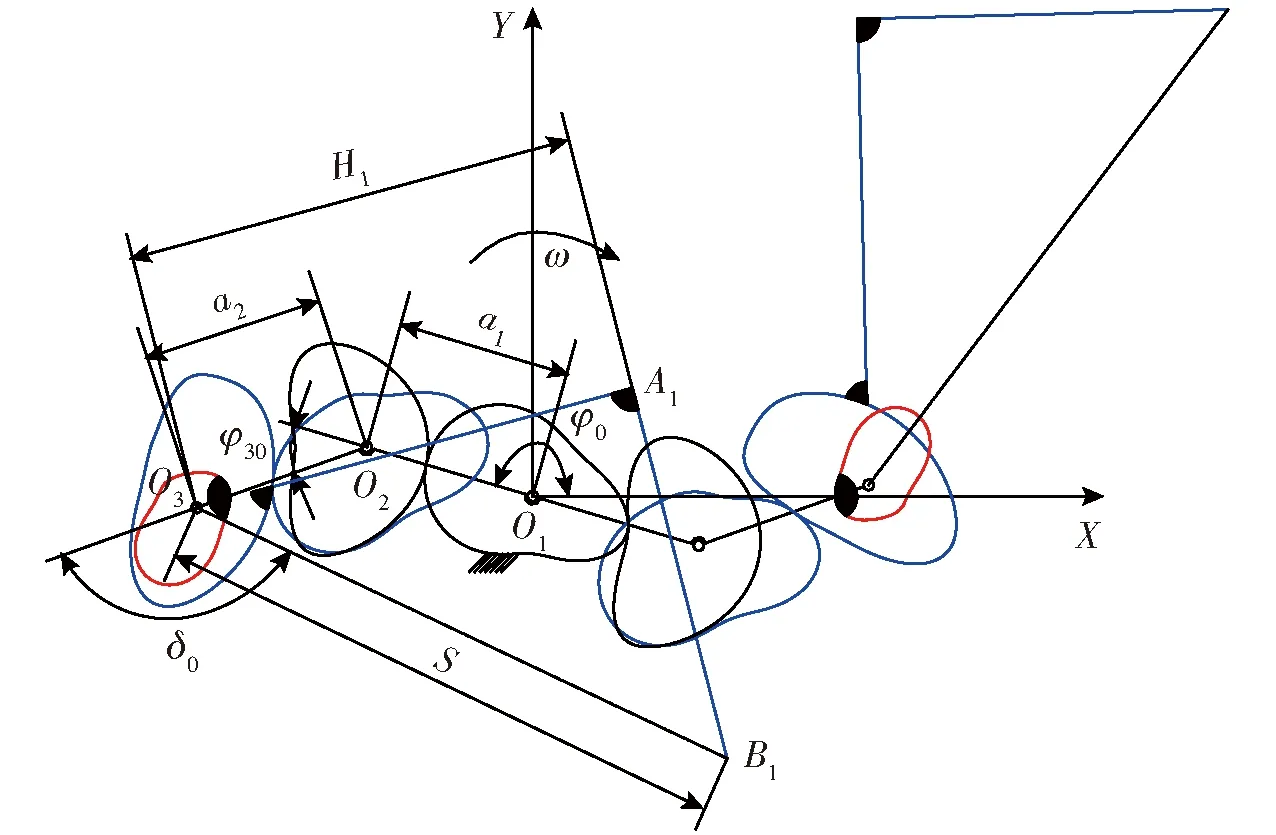
图4 取苗栽植机构结构简图Fig.4 Structure sketch of seedling-picking and planting mechanism
2.2.1取苗栽植机构运动学分析
取苗栽植机构结构简图如图4所示。规定行星架逆时针转动角度为正,βj(φ)为齿轮j相对行星架的转角,φj(φ)为齿轮j的绝对转角。行星架的初始安装角为φ0,当行星架顺时针转过φ时,各角度分析如下:
行星架的绝对转角为
φH(φ)=φ0-φ
(6)
太阳轮相对行星架的转角和绝对转角分别为
(7)
中间轮A相对行星架的转角和绝对转角为
(8)
式中r1(i)——一级传动太阳轮节曲线极径,mm
a1——相互啮合的一级传动齿轮(太阳轮和中间轮A)中心距,mm
因为齿轮中间轮B和中间轮A是同轴固定,所以中间轮B相对行星架的转角和绝对转角为
(9)
式中φ30——行星架拐角所引起的中间轮B的初始安装角,(°)
行星轮相对行星架的转角和绝对转角为
(10)
式中r2(i)——二级传动中间轮B节曲线极径,mm
a2——相互啮合的二级传动齿轮(中间轮B和行星轮)中心距,mm
在以O1为原点建立的直角坐标系中,各点的坐标分析如下:
太阳轮转动中心坐标为
(11)
式中H——草莓株距,mm
中间轮A和中间轮B转动中心坐标为
(12)
行星轮转动中心坐标为
(13)
栽植臂拐点A1的坐标为
(14)
式中H1——非圆行星轮转动中心O3到栽植臂拐点A1的距离,mm
S——非圆行星轮转动中心O3到栽植臂秧针尖点B1的距离,mm
栽植臂秧针尖点B1的坐标为
(15)
其中
γ1=-φ+β4(φ)+δ0
(16)
式中δ0——栽植臂的初始安装角,(°)
2.2.2挖穴机构运动学分析
(1)挖穴拨叉转动中心O6的坐标求解
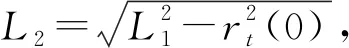
(17)
式中δ1——转动中心O6的初始安装角,(°)
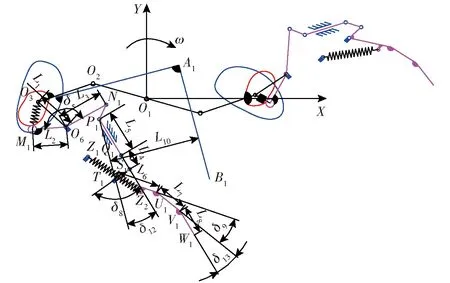
图5 挖穴机构结构简图Fig.5 Structure sketch of hole-digging mechanism
挖穴拨叉转动中心O6的坐标为
(18)
(2)挖穴拨叉两端点M1和N1的坐标求解
在拨叉拉簧作用下,挖穴凸轮和挖穴拨叉始终接触,假设挖穴凸轮旋转运动,挖穴拨叉随之旋转,设接触点为(xA(θ),yA(θ)),有
(19)
其中
tφ(k)=(φ6-k+δ1)π/180-arccos(rt(0)/L1)
(20)
式中tφ(k)——挖穴凸轮绝对旋转角度,rad
设点A和点O6的距离误差为
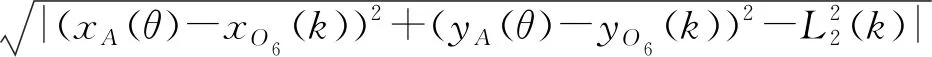
(21)
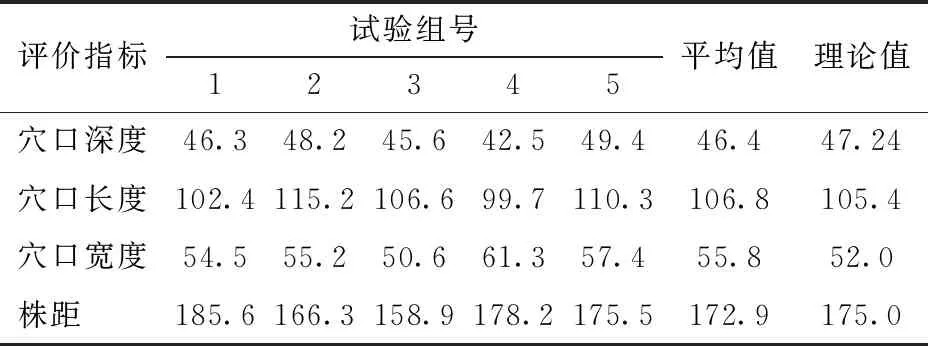
式中θ、k为循环变量,θ循环嵌套于k循环中,循环次数均为360次,每循环一次k,θ计算360次,在编写的程序中得出此时满足下面条件的θ,可知有2个值满足条件,此时将循环分为0≤k≤z和z ds(θ)≤ξ (22) 其中z、ξ为判断值,本文取ξ=5 mm。 由所判断出的θ计算出每个k循环下连杆O1M1的角度为 (23) 式中δ3(k)——连杆O1M1与水平方向夹角,rad 所以挖穴拨叉一端点M1的坐标为 (24) 其中 δ3(φ)=δ3(k) (25) 挖穴拨叉一端点N1的坐标为 (26) 式中L3——O6N1长度 δ5——O6M1与O6N1夹角 (3)连杆各铰链点以及各拐点坐标计算 设秧针A1B1旋转过程任意时刻的斜率为 (27) 设未加P1Q1与A1B1夹角δ12,连杆P1Q1的斜率和秧针A1B1的斜率相等,即k2(φ)=k1(φ),且两直线相距L10,此时利用挖穴凸轮的初始时刻即可计算出未加δ12时连杆P1Q1的直线方程,因为连杆N1P1的长度为L4,所以可推导出加入δ3(φ)和δ12后P1的坐标,此处省略推导过程,得出(xP1(φ),yP1(φ))。由于所设计的ΔQ1S1T1为等腰三角形,且腰长为L4,上述过程中还可求出固定于栽植臂上的T1的坐标。 铰链点Q1坐标为 (28) 其中 γ2=δ3(φ)-δ4(φ)-δ7(φ) (29) (30) (31) 式中δ4(φ)——O6N1与N1P1夹角,rad δ7(φ)——P1Q1与水平方向夹角,rad L5——P1Q1长度,mm 根据Q1点、T1点和lQ1S1=lS1T13个已知条件可得铰链点S1坐标(xS1(φ),yS1(φ)),推导过程省略。 挖穴铲拐点U1坐标为 (32) (33) 式中δ10(φ)——S1T1与水平方向夹角,rad δ8——S1T1与T1U1的拐角,(°) L6——T1U1长度,mm 挖穴铲拐点V1坐标为 (34) 式中δ9——U1V1与T1U1的拐角,(°) L7——U1V1长度,mm 挖穴铲尖点W1坐标为 (35) 式中δ13——U1V1与V1W1的拐角,(°) L8——V1W1长度,mm 各个部件的位移(转角)对时间求一阶导数和二阶导数即可得到其速度(角速度)和加速度(角加速度)。 全自动草莓钵苗移栽机构采用传统优化方法很难解决多参数、多目标、强耦合性优化难题。因此,本文根据农艺要求、理论分析与目标函数,设计了全自动草莓钵苗移栽机构优化软件,简化了设计过程,缩短了研发周期。 本文根据移栽机构数学模型、农艺要求及机构特点提出23个优化目标,建立相应目标函数,将几何目标数值化,同时给出了优化目标的最优范围。优化目标是判断优化参数是否满足要求的重要指标[26],建立优化目标如下:两栽植臂作业时互不干涉;两栽植臂作业时与秧箱不干涉;取苗角介于310°~320°之间;取苗取出段直线长度大于45 mm;推苗角介于260°~280°之间;钵苗移栽角度差介于40°~60°之间;推苗后苗与地面夹角介于70°~110°之间;栽植臂不推倒已栽秧苗;齿轮箱距地面高度大于25 mm;尖嘴的穴口宽度小于5 mm;挖穴和移栽轨迹高度都大于150 mm;挖穴铲铰链点与秧箱不干涉;挖穴铲与秧箱不干涉;挖穴铲与栽植臂后盖不干涉;绝对运动穴口长度介于85~110 mm之间;穴深介于40~50 mm;挖穴铲不推秧;绝对运动穴口中心与秧苗的中心偏移量小于20 mm;挖穴铲不与秧针干涉;铰链点与地面最近的距离大于25 mm;传动箱不与秧箱干涉;秧针取苗摆角小于5°;非圆齿轮模数大于2.5 mm。 全自动草莓钵苗移栽机构优化设计难点在于实现取苗轨迹和实现挖穴轨迹的两套机构之间的配合。根据所建立的运动学理论模型和数字化优化目标,基于Visual Basic 6.0设计了移栽机构辅助分析优化设计软件[27],软件可对机构的结构尺寸、位置和运动状态进行实时运动模拟,通过人机交互,以显示条辨别目标优劣,通过调节参数对移栽机构目标进行优化。通过辅助分析优化设计软件,最终获得一组满足全自动草莓钵苗移栽机构要求的结构参数,如图6所示。 图6 移栽机构优化软件界面Fig.6 Interface of optimization software for transplanting mechanism 非圆齿轮轮系包括主动轮非圆齿轮和从动轮非圆齿轮(共轭齿轮),非圆齿轮由每个轮齿的齿形和轮齿的过渡曲线组成,每一个轮齿的齿形和过渡曲线都不一样[23]。 由节曲线方程式可推导出非圆齿轮齿形方程式[28],确定齿形的解析图见图7。 图7 齿形解析图Fig.7 Analytical diagram for gear profile 右齿形方程为 xR=xg±scosαncosu (36) yR=yg±scosαnsinu (37) 左齿形方程为 xL=xg∓scosαncosu (38) yL=yg∓scosαnsinu (39) 式中 (xg,yg)——节曲线与齿形法线交点坐标,mm u——节曲线上点(xg,yg)的切线正方向与X轴正方向的夹角,rad s——由节曲线上点(xg,yg)到节曲线与齿形交点的节曲线弧长,mm αn——刀具齿形角(一般为20°),(°) 式中正负号取决于u所在象限;上面的符号适用于节曲线上齿形线上的点;下面的符号适用于节曲线下齿形线上的点。 非圆齿轮的过渡曲线形成原理是:插齿刀和被切非圆齿轮在P点开始啮合时,刀尖E点轨迹的连线形成过渡曲线[28],插齿刀切齿时过渡曲线的原理如图8。 图8 过渡曲线解析图Fig.8 Analytical diagram of transition curve 右过渡曲线方程为 x′R=xg+dcos(u+λ2+π/2) (40) y′R=yg+dsin(u+λ2+π/2) (41) 左过渡曲线方程为 x′L=xg+dcos(u-λ2+π/2) (42) y′L=yg+dsin(u-λ2+π/2) (43) 式中d——插齿刀节曲线上l点到插齿刀尖点E的距离,mm λ2——插齿刀节曲线上l点和插齿刀圆心O8的连线与插齿刀节曲线上l点和插齿刀尖点连线的夹角,rad 插齿刀节曲线上点l和非圆节曲线上点l′到啮合点P点的曲线距离相等。由以上理论可在Visual Basic 6.0软件中编写齿形成型程序和过渡曲线成型程序。利用程序导出所需的齿形CAD文件和过渡曲线CAD文件。将所有的齿形线和过渡曲线合并和修剪,从而得到最终的非圆齿轮齿廓线,如图9所示。 图9 主动轮齿廓形成过程Fig.9 Formation process of tooth profile for driving gear 用相同原理成型共轭非圆齿轮,在NX 10.0三维软件中拉伸出实体。将非圆齿轮导入ADAMS动力学仿真软件中,进行运动仿真,验证非圆齿轮成型软件编写的正确性。 根据优化的参数对移栽机构进行结构设计,利用NX 10.0软件完成三维建模与装配,并将装配体导入ADAMS 2010软件中,进行虚拟样机仿真,得出全自动草莓钵苗移栽机构的秧针尖点和挖穴铲尖点的运动轨迹,如图10所示。仿真轨迹与理论轨迹基本一致,初步验证了移栽机构理论设计的正确性。 图10 虚拟样机仿真轨迹Fig.10 Simulation trajectory of virtual prototype 为缩短物理样机的研制时间、降低复杂零件的加工成本、加快样机研制速度,应用工业级3D打印技术完成主要零部件的实体成型,为后期模具开发奠定了良好的基础。为了保证机构的可靠性,部分零部件采用金属材质加工。 将装配好的物理样机安装在试验台架上[29],利用高速摄像试验验证其性能及轨迹和姿态。设定机构转速为40 r/min,利用Phantom V5.1高速摄像机完成移栽机构运动轨迹的拍摄。通过高速摄像机及分析软件获得了全自动草莓钵苗移栽机构在开始进入土钵、完全夹紧土钵、土钵完全离开钵盘、开始挖穴、栽植推秧瞬间和栽植完成等实际工作关键位置与时刻的轨迹与姿态图像,如图11所示。通过分析图像可知,取苗、挖穴和栽植均满足设计要求,且效果良好;同时通过后期数据处理,得到物理样机秧针尖点与挖穴铲尖点运转过程中的相对运动轨迹,如图12所示。 图11 移栽机构关键位置Fig.11 Key positions of transplanting mechanism 图12 高速摄影验证试验Fig.12 High-speed photography verification test 将物理样机所得实际轨迹与优化设计软件所得理论轨迹和虚拟仿真轨迹对比可知,结果基本保持一致,验证了移栽机构设计的可行性与合理性。由于物理样机试验中的机器振动原因,轨迹会受到影响,但这些因素造成的误差均在合理范围内。 图13 取苗、挖穴和栽植试验Fig.13 Test of picking seedling, digging holes and planting 为了进一步验证所研制的全自动草莓钵苗移栽机构的实际工作情况,对其进行物理样机台架性能试验研究[30-31],如图13所示。在东北农业大学工程学院兼光型植物工厂实验室进行育苗,钵苗满足移栽要求后,在东北农业大学农业机械化实验中心进行性能验证试验。 试验穴盘尺寸需满足草莓育苗期间的空间要求,故采用5×10穴的塑料软质穴盘,钵盘长480 mm、宽255 mm,穴口上口径45 mm×45 mm、下口径20 mm×20 mm、钵深40 mm,每穴间距50 mm,穴钵底部的圆孔直径为10 mm。试验选用草莓品种为“牛奶”草莓,栽植株距150~200 mm(本文株距取175 mm),行距为200~300 mm,苗龄为33 d,平均苗高120 mm,每穴一株。将育秧基质与黑土按质量比1∶1混合[32]。 考虑3D打印材料的强度,试验时移栽机构顺时针旋转,转速为40 r/min,土槽向左直线运动,速度为0.23 m/s,共对2盘钵苗共100穴进行取苗、挖穴和栽植试验。试验过程中,机构运转平稳。成功将钵苗完全从钵盘中取出的秧苗共有92株,取苗成功率为92%;对挖穴试验中穴口的深度、长度、宽度和栽植株距进行测量记录,选取5组每组5次试验数据的平均值,如表1所示,形成穴口的平均深度、长度和宽度分别为46.4、106.8、55.8 mm,平均栽植株距为172.9 mm;成功栽入穴中的钵苗共85株,栽入成功率为85%;以上试验数据均符合草莓移栽机构设计要求[33],进行的相关性能试验验证了移栽机构的可行性与实用性。 分析未取出秧苗的主要原因包括:取苗过程连带出相互连根的邻苗从而导致的空穴、穴盘内钵苗未出苗和生长不佳导致秧苗幼小盘根不理想等;而未栽入穴口的原因主要是移栽过程机器的振动使土钵基质松散,或钵苗本身盘根不佳,导致移栽过程中滑落或推秧不准确等。以上问题可通过后期对育秧或机构等完善来提升整体性能。 表1 试验结果Tab.1 Results of test mm (1)提出了一种全自动草莓钵苗移栽机构,结构简单、成本低,可一次性完成取苗、输送、挖穴和移栽一系列移栽工序。 (2)建立了机构运动学理论模型,并基于Visual Basic 6.0设计了针对全自动草莓钵苗移栽机构的辅助分析优化设计软件和非圆齿轮成型软件,最终得到一组满足草莓钵苗移栽要求的结构参数。 (3)进行了虚拟仿真验证与物理样机的研制,开展了高速摄像台架验证试验,得出了理论轨迹、虚拟仿真轨迹和台架实际轨迹基本一致的结论,验证了机构设计的正确性。 (4)完成了试验所需草莓钵苗的培育工作,在试验台架上进行了取苗、挖穴和移栽试验,结果表明取苗成功率为92%,栽植成功率为85%,平均栽植株距为172.9 mm,所挖穴口深度、长度和宽度效果良好,均满足农艺要求,试验结果证明了所设计移栽机构性能的实用性。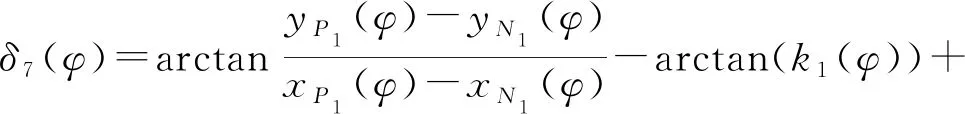
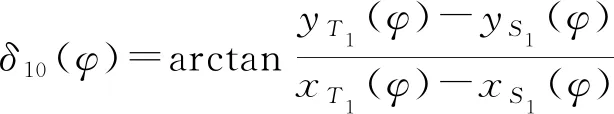
3 计算机辅助分析与优化软件设计
3.1 机构优化目标的确定
3.2 移栽机构优化软件设计

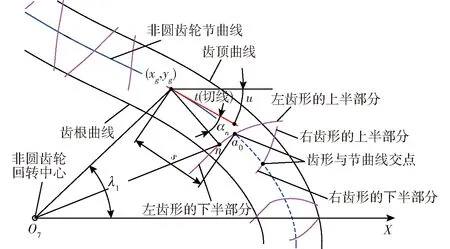
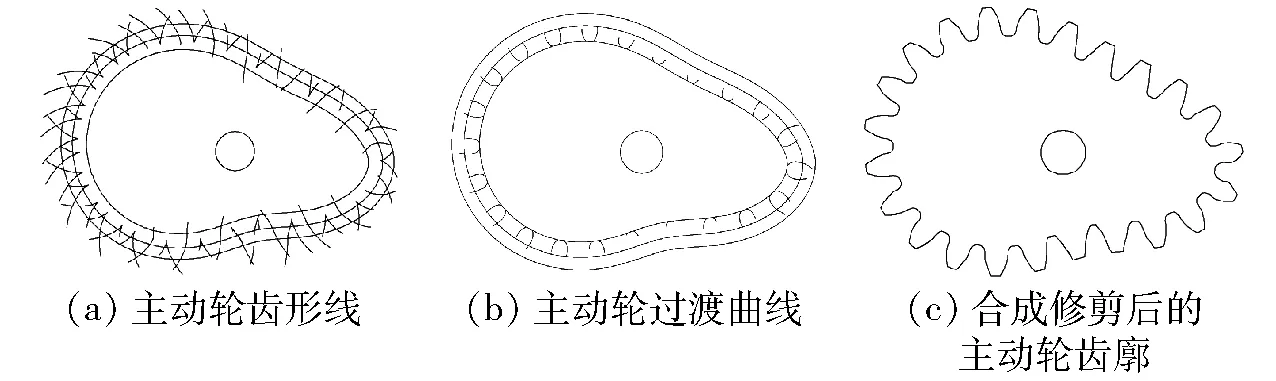
3.3 非圆齿轮成型软件

4 虚拟样机仿真与物理样机试验
4.1 虚拟样机仿真验证与物理样机加工
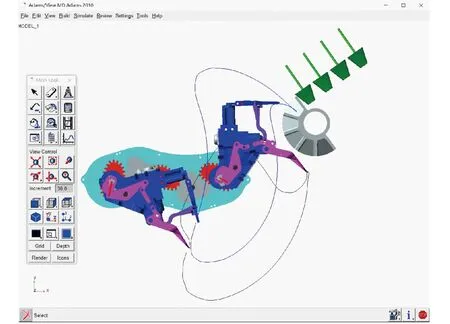
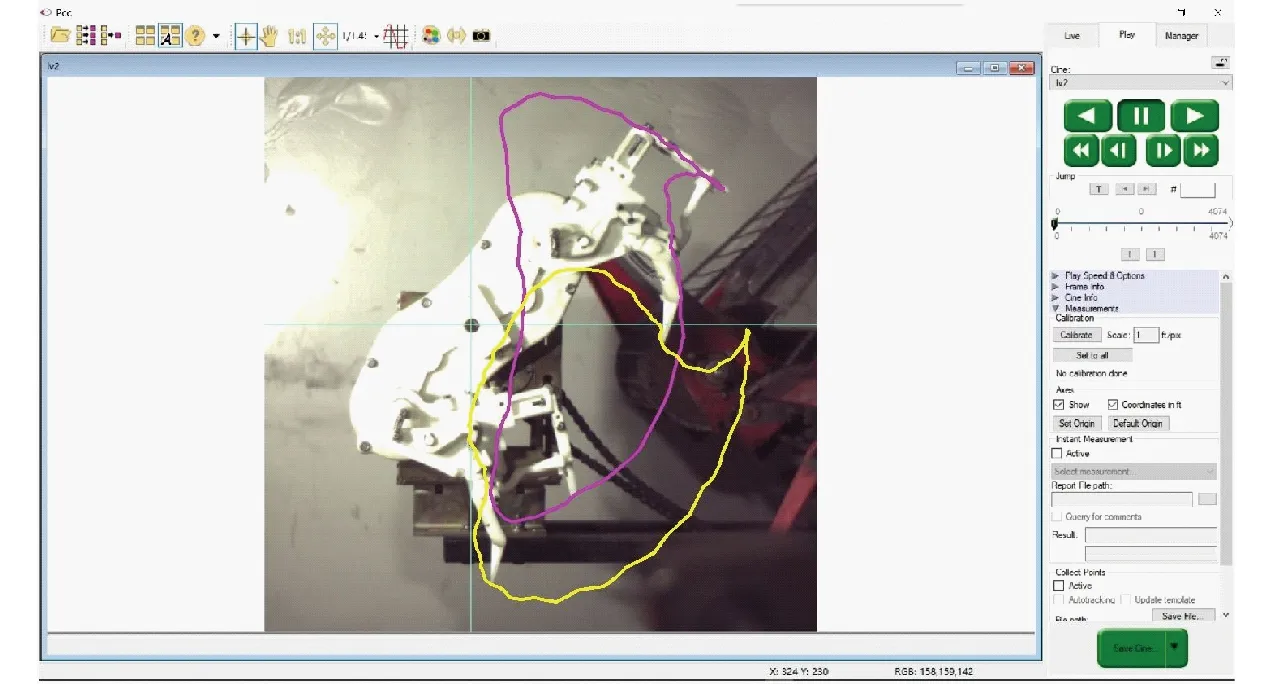
4.2 高速摄像试验验证

4.3 物理样机台架试验

5 结论

