改进遗传算法PID参数优化在吹贯蒸汽流速控制中的应用

汤伟　杨润珊　孙振宇

摘 要：纸机干燥部吹贯蒸汽流速控制是解决烘缸积水问题的一项重要措施。吹贯蒸汽流速控制通常采用PID控制器，而传统的PID控制方法的控制精度较低、参数整定耗时较长，难以达到理想的控制效果。本课题在对基本遗传算法进行分析的基础上，提出了一种改进的遗传算法，并将该算法用于PID控制器参数优化，实现对纸机干燥部吹贯蒸汽流速的精确控制。MATLAB仿真实验结果表明，与常规PID控制器和基于基本遗传算法的PID控制器相比，基于改进遗传算法的PID控制系统具有响应速度快、超调量小、鲁棒性强的优点，能够获得理想的控制效果。文中所述算法已投入实际应用，明显提高了二次蒸汽的利用效率，能够获得可观的经济效益。

关键词：吹贯蒸汽流速;遗传算法;PID参数优化;干燥部

中图分类号：TS736

文献标识码：A

DOI：10.11981/j.issn.1000-6842.2019.01.60

在纸张的干燥过程中，烘缸内通入蒸汽的热量通过烘缸表面传递给纸张，纸张中水分由于吸收热量而蒸发，达到脱除纸张水分的目的[1]。传统烘缸干燥存在的最大问题就是蒸汽冷凝放热后形成的冷凝水不能及时排出，会随烘缸一起运动，在烘缸内壁形成冷凝水环，影响纸机干燥效率、纸幅干燥质量以及烘缸运行的稳定性[2]。纸机干燥部吹贯蒸汽流速控制是解决烘缸积水问题的一项重要措施[3]。吹贯蒸汽是指进入烘缸内但没有发生冷凝的那部分蒸汽，它在烘缸内与冷凝水混合形成气液两相流，经过虹吸管排出烘缸而进入闪蒸罐内，是烘缸冷凝水排除的动力[3]。吹贯蒸汽流速控制通过在闪蒸罐蒸汽出口管道水平位置上安装孔板，测量孔板两侧蒸汽压差，并通过控制排气阀和热泵开度将吹贯蒸汽流速维持在一个适当的范围。然而，吹贯蒸汽流速控制过程具有时滞性、非线性、难以精确建模等特点，控制难度较大。因此对纸机干燥部吹贯蒸汽流速控制的优化成为了亟待研究的问题。

目前，纸机干燥部吹贯蒸汽流速控制通常采用PID控制，由于PID控制具有结构简单、实现方便、适应性强等特点，在我国造纸行业中被广泛采用。但是PID控制最大的缺点是参数不易整定，容易产生振荡，并且会出现超调。常规PID控制器参数整定多采用试验加试凑的方式进行人工优化[4]。这种优化工作不仅需要熟练的技巧，而且相当费时。目前PID参数优化的方法有很多，如单纯形法、专家整定法、爬山法等，虽然这些方法都具有良好的寻优特性，但存在一些弊端：单纯形法对初值比较敏感，容易陷入局部最优解;专家整定法则需要太多的经验，整理知识库困难[5]。本课题采用遗传算法优化PID参数，该方法是一种不需要任何初始信息，就能高效、并行、全局性地搜索最优解的方法。近年来，国内外学者对遗传算法进行了各种各样的改进，总的来说主要在两个方面：一是改进自身基因的遗传算法[5]，二是与其他算法相结合的混合遗传算法[6]，所有的改进都是为了克服“早熟”问题，提高遗传算法的全局寻优能力以及加快算法的收敛速度。本课题引入了评价种群“早熟”程度的新指标，对基本遗传算法的交叉算子、变异算子进行改进，并增加当前最优追踪策略，得到一种改进的自适应遗传算法。对吹贯蒸汽流速PID控制器参数整定模型进行仿真实验，通过和基于基本遗传算法的PID参数整定法以及常规PID参数整定法的仿真对比，验证了改进遗传算法的良好效果。

1 吹贯蒸汽流速控制原理

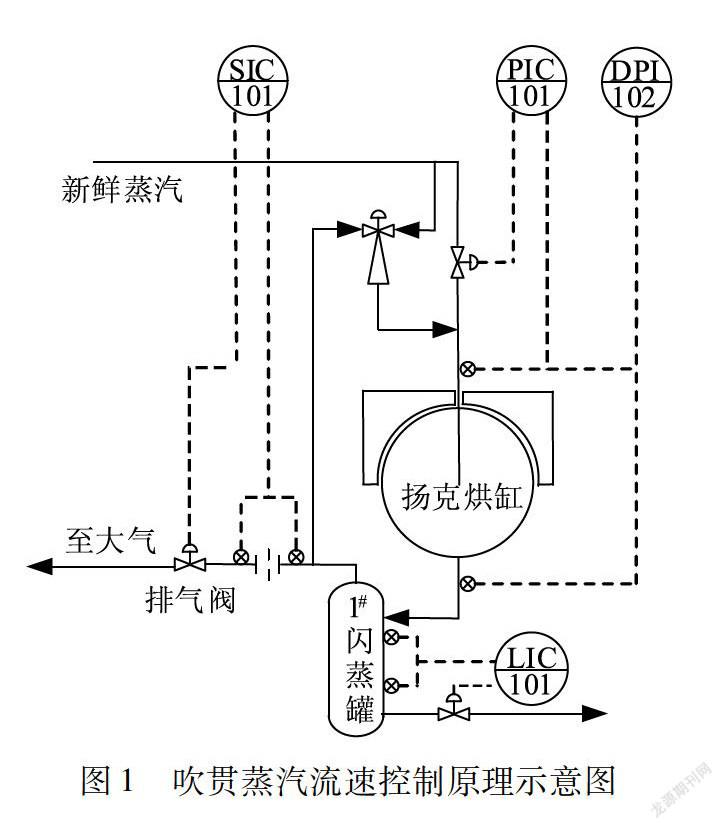
吹贯蒸汽流速控制原理如图1所示。由于闪蒸罐出口蒸汽压差直接反映了烘缸内吹贯蒸汽量，因此在闪蒸罐蒸汽出口管道水平位置上安装孔板流量计，通过孔板两侧二次蒸汽压差来测量吹贯蒸汽流量，并与排气阀和热泵组成控制回路，通过调节排气阀和热泵开度将吹贯蒸汽流速维持在一个适当的数值。其中孔板流量计工作原理如图2所示，孔板对闪蒸出来的蒸汽通过节流减压作用产生前后压差，孔板两侧的压差在一定程度上反映了蒸汽流过孔板的流量大小，因此只要稳定了吹贯蒸汽的流量，也就稳定了烘缸内的压力和冷凝水速率。

在纸机干燥部蒸汽冷凝水系统运行时，一旦烘缸积水就会降低纸张与蒸汽的热交换效率，使得从烘缸出来的蒸汽密度变大，导致经过闪蒸后的吹贯蒸汽通过孔板时形成的壓差减小，此时增大排气

阀和热泵开度，吹贯蒸汽经过热泵的增压作用会在其出口位置形成较强的气流从而对烘缸内的积水进行吹贯以排出冷凝水[7]。随着冷凝水的排出和排气阀开度的增大，吹贯蒸汽在孔板两侧形成的压差开始回升，进而减小排气阀和热泵的开度以稳定孔板两侧的压差，即稳定吹贯蒸汽流速，从而提高二次蒸汽的利用效率，减少闪蒸罐二次蒸汽的浪费。

2 遗传算法原理及改进方法

遗传算法（Genetic Algorithms，简称GA）是1962年由美国Michigan大学Holland教授提出的模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优化方法[8]。遗传算法是一种随机性全局搜索和优化的方法，它借鉴了达尔文进化理论和孟德尔遗传学说，模仿了生物进化的机制，是一种高效、并行、全局性的搜索方法。遗传算法将适应度函数作为一个选择条件，通过反复的搜索，使种群不断得到优化[9]。遗传算法的基本思想是把待优化参数进行编码，然后由若干个位串形成初始种群作为待求问题的候选解，通过选择（select）、交叉（crossover）、变异（mutation）进行操作，不断迭代优化，直到满足终止条件为止。

2.1 基本遗传算法

基本遗传算法流程如下：①随机产生初始种群，个体数目一定，每个个体表示染色体的基因编码;②计算个体适应度，并判断是否符合停止准则，若符合，输出最佳个体及代表的最优解并结束计算，否则转向③;③依据适应度选择再生个体，适应度高的个体被选中的概率高，适应度低的个体可能被淘汰;④按照一定的交叉方法和交叉概率，生成新的个体;⑤按照一定的变异方法和变异概率，生成新的个体;⑥如果由交叉和变异产生新的种群，则返回到步骤②。

基本遗传算法具有全局搜索能力、潜在的并行性、可扩展性等优点;但是算法的局部搜索能力较差，在进化后期搜索效率较低，且容易产生“早熟”收敛[10]。

2.2 改进遗传算法

针对影响遗传算法的收敛性质及收敛速度的参数选择，在实际应用中应合理选择与设计。本课题采用的改进遗传算法有如下特点。

（1）关于染色体的编码：在对控制器参数的优化设计部分，由于本问题属于连续函数的优化问题，二进制编码增加了算法的复杂性，还有许多缺点，如精度不高、个体长度大、占用计算机内存多、不能直接反映问题的固有结构、用高级语言编写程序繁琐等不足，因此采用实数编码。

（2）关于遗传算法的操作程序：由于基本遗传算法的操作程序是较为规范的进化过程，且简单易行，对于大部分的实际应用问题都具有很强的适用性与优越性。因此，本课题中的遗传算法仍采用这一操作程序。

（3）关于改善遗传算法“早熟”问题：引入了评价种群“早熟”程度的新指标。种群发生“早熟”的主要表现为：种群内适应度暂时最大的一些个体相互重复或趋同，使得它们有较大的概率参与下一代的选择复制操作，且它们之间交叉后的子代也不会与父代有太大的变化，导致遗传算法寻优过程十分缓慢，降低搜索效率[10]。因此，正确判断一个种群是否会发生“早熟”主要看这个种群当前适应度最大的那些个体是否重复或相互趋同。基于此思想，提出了一种评价种群“早熟”程度的新指标，优良个体趋同度Δ，定义如下。

设第t代种群是由M个个体组成，平均适应度值为Ft，最优个体适应度值为Ftmax，Ftmax代表适应度大于Ft的个体平均适应度，则：

Δ=100（Ftmax-Ftmax）（1）

指标Δ可以用来表征种群的早熟程度。计算Δ时不涉及那些适应度低于平均适应度的较差个体，从根本上避免了较差个体带来的不利影响，可更清楚地从概念上反映种群中当前适应度最大的那些个体之间的趋同程度，从而能更准确地描述种群个体发生“早熟”的程度。

（4）关于自适应交叉与变异：用不变的控制参数来控制遗传进化，很容易导致“早熟”，降低算法的搜索效率。目前，调整遗传算法控制参数较好的方法是动态自适应技术，其基本思想是使Pc、Pm在进化过程中根据种群的实际情况，随机调整大小。具体做法为当种群趋于收敛时，减小Pc、增大Pm，即降低交叉概率，提高变异概率，以保持种群的多样性，避免“早熟”;当种群个体发散时，增大Pc、减小Pm，即提高交叉的概率，降低变异的概率，使种群趋于收敛，增加算法的收敛速度。

基于前述评价种群早熟程度的新指标，优良个体趋同度Δ，提出如下的自适应调整遗传算法控制参数的新策略，使得交叉概率Pc、变异概率Pm在进化过程中随着Δ的变化而变化，数学描述如下：

Pc=11+exp（-k1·Δ）（2）

Pm=1-11+0.1exp（-k2·Δ）（3）

式中，k1、k2>0，由于Δ≥0，所以Pc的取值范围为[0.5，1]，Pm的取值范围为[0，0.09]。从式（2）和式（3）可见，在进化过程中，Pc、Pm根据Δ取值的不同而动态地自适应调整。当种群个体趋于离散，即Δ变大时，Pc增大、Pm减小，种群开发优良个体的能力增强;当种群个体趋于收敛，即Δ变小时，Pc减小、Pm增大，种群产生新个体的能力增强。

（5）增加当前最优追踪策略：通过改进遗传算法内部交叉和变异算子，可以增加种群的多样性，从而更快找到最优解，然而一定程度上也破坏了优良种群。采用当前最优追踪策略，通过保存每一代的当前最优解，可以对每次进化的结果进行修正，避免优良基因的丢失。

3 基于改进遗传算法的PID参数优化

PID控制器具有结构原理简单、适应性强的特点，控制量u与偏差e=r-y（其中，r为设定值，y为系统的输出值）满足式（4）关系。

u（t）=Kpe（t）+1Ti∫t0e（t）dt+Tdde（t）dt

=Kpe（t）+Ki∫t0e（t）dt+Kdde（t）dt（4）

式中，Kp表示比例因子，Ti表示积分时间常数，Td表示微分時间常数;Ki=Kp/Ti表示积分系数，Kd=Kp·Td表示微分系数。

基于改进遗传算法的PID控制就是在PID控制的基础上引入上述改进遗传算法，通过改进遗传算法对PID控制参数Kp、Ki、Kd进行整定，最终得到良好的控制效果。其控制框图如图3所示。

一般控制系统要求被控系统能够很快跟随系统的输入并达到稳定状态，为了能够获得满意的动态特性，本课题采用误差绝对值时间积分性能指标作为参数选择的目标函数，为了防止控制能量过大，在目标函数中加入控制输入的平方项，选式（5）作为最优目标：

J=∫∞0（w1·e（t）+w2·u2（t））dt+w3·tu（5）

式中，e（t）为系统误差，u（t）为控制器输出，tu为上升时间，w1、w2、w3为权值。

为避免超调，采用了惩罚功能，即一旦产生超调，将超调量作为最优指标的一项，此时最优指标为：

if ey（t）<0，J=∫∞0[w1·e（t）+w2·u2（t）+w4·ey（t）]dt+w3·tu（6）

式中，w4为权值，且w4w1，ey（t）=y（t）-y（t-1），y（t）为被控对象输出。

首先由遗传算法产生初始种群，并将种群信息赋予PID参数，然后根据适应度函数计算每一组参数的适应度值，接着对种群进行遗传操作，不断进化，直到找到群体中的最优个体，输出PID控制器的最优参数。改进遗传算法优化PID参数的具体流程如图4所示。

4 仿真实验与分析

本课题运用MATLAB中的Simulink进行仿真实验，对纸机干燥部吹贯蒸汽流速控制系统采取简化一阶惯性加延时的环节，通过阶跃响应作图法来获取其数学模型为：

G（s）=1.454.7s+1e-3s（7）

下面采用常规PID整定法、基本遗传算法、改进遗传算法3种方法来对PID参数进行整定仿真对比实验。其中，Kp、Ki、Kd 3个待优化参数的取值范围为[0，1]。两种遗传算法中，种群规模均设为30，最大迭代次数均为100次。基本遺传算法中，设定交叉概率与变异概率分别为Pc=0.9，Pm=0.01，改进遗传算法中，根据公式另外设置系数k1=k2=0.8。

图5为目标函数值在两种遗传算法分别整定下的优化曲线。对比两条曲线可以看出，两种遗传算法最后优化的指标值几乎一致，虽然传统遗传算法在第44代已经接近最优，但收敛极慢，直到进化至第92代才达到最优;而改进遗传算法在第3代已经接近最优，在第28代就达到了最优，表明改进遗传算法的收敛速度大大提高。表1为两种遗传算法分别进行10次独立运行的运行效果比较。

从表1可知，基本遗传算法执行10次的过程中，收敛的次数只有4次，且收敛代数都较大，而且Δ指标值都较小，这表明种群中当前适应度最大的那些个体之间的趋同程度较大，即算法“早熟”的程度较严重。而本课题提出的改进遗传算法在执行10次的过程中，收敛的次数为8次，其收敛代数也比基本遗传算法有较大的改进，而且Δ指标值都较大，这表明种群中当前适应度最大的那些个体之间的趋同程度较小，即算法“早熟”的现象明显改善。由此可见，改进遗传算法无论在算法的稳定性还是收敛速度上都较基本遗传算法有了很大改善，并且较好地抑制了算法“早熟”现象。

图6为在总仿真时间为100 s条件下的不同PID参数整定方法的响应曲线。由图6可知，经两种遗传算法优化后的PID模型，在调节时间和超调量上都得到了很大的改善;而改进遗传算法的调节时间比基本遗传算法缩短了9 s，响应速度更快，而且无超调，显然改进遗传算法能够更有效地优化出较好的PID控制参数。

3种方法整定的PID参数及控制性能指标如表2所示。从图6和表2中可以看出，与基本遗传算法的PID控制系统和常规PID控制系统相比，基于改进遗传算法的PID控制响应速度快，无超调量，稳定性好，具有较优的动态性能，并且减少了算法运算时间，可以有效解决PID控制器参数整定难的问题。

在实际的控制过程中，吹贯蒸汽流速数学模型常常会受干扰、噪声和非线性等因素的影响而发生变化。假设模型失配时的传递函数为：

G（s）=1.605.2s+1e-2.7s（8）

采用上述调整好的仿真模型来对此时模型失配的情况进行仿真，并在第80 s时给系统加入10%的干扰。图7为模型参数失配时在常规PID整定法、基本遗传算法以及改进遗传算法优化下的响应曲线。

由图7可知，当模型参数发生变化以及出现较大干扰，并且失配模型的时滞现象更严重时，3种控制方案的控制效果都比模型匹配时要减弱。但是两种遗传算法优化的PID模型都比常规PID整定法具有更强的鲁棒性，并且经改进遗传算法优化的PID控制器比基本遗传算法优化的PID控制器的响应速度更快。其结果充分证明了基于遗传算法的PID控制系统较常规PID控制系统在响应速度、超调量以及延迟时间、增强系统抗干扰能力等特性上均有明显优势。并且经改进的遗传算法优化的PID控制系统具有更好的控制性能和鲁棒性。

5 算法的实现及应用

为了将基于改进遗传算法的PID控制系统应用于工业现场，本系统采用S7-300系列PLC为开发平台，在闪蒸罐出口安装孔板流量计，通过孔板两侧二次蒸汽压差来测量吹贯蒸汽流速，并使用OPC技术，通过在上位机中MATLAB与WinCC变量进行数据交换，将现场采集的压差实时数据传输至MATLAB，经过MATLAB中改进遗传算法处理，得到优化后的PID控制参数，之后将相应结果送回WinCC，通过调整PID控制参数从而调节放气阀和热泵开度，实现吹贯蒸汽流速的精确控制。本系统已在河北某造纸厂干燥工段投入应用。图8为吹贯蒸汽流速控制系统稳定运行一段时间的实时运行曲线。由图8可知，闪蒸罐出口压差能很好地跟踪设定值，自调节能力较好，即表明吹贯蒸汽流速控制系统控制性能较好，满足了工程实际的需要。

6 结 语

本课题提出的基于改进遗传算法优化PID控制既提升了遗传算法的收敛速度，又显著改善了基本遗传算法的“早熟”问题。MATLAB仿真结果表明，在吹贯蒸汽流速控制中，基于遗传算法优化的PID控制系统比常规PID控制系统的控制精度更高，并且基于改进遗传算法优化的PID控制系统比基于基本遗传算法优化的PID控制系统的响应速度更快，超调量更小，系统鲁棒性也更好。吹贯蒸汽流速控制系统运行效果表明，闪蒸罐出口压差能很好地跟踪设定值，自调节能力较好，满足工程实际的需要，并且能显著提高二次蒸汽的利用效率和造纸企业的经济效益。

参 考 文 献

[1] Zhong Yilian. Measurement and Control Methods of the Steam Condensate System of Paper Machine[J]. China Pulp & Paper， 2013， 32（3）： 40.

钟益联. 纸机蒸汽冷凝水系统测控方法介绍[J]. 中国造纸， 2013， 32（3）： 40.

[2] Dong Jixian， Shi Yun， Tang Wei. An analysis and research of drying mechanism of multi-channel cylinder dryer[J]. Chinese Journal of Paper Industry， 2016， 37（6）： 26.

董继先， 史 韵， 汤 伟. 造纸机多通道烘缸干燥机理的分析与研究[J]. 中华纸业， 2016， 37（6）： 26.

[3] Tang Wei， Wang Qi， Chen Hang， et al. Steam and Condensate System for Chinese High Speed Tissue Paper Machines[J]. Paper Science and Technology， 2014， 33（6）： 124.

湯 伟， 王 琦， 陈 航， 等. 国产高速卫生纸机蒸汽冷凝水系统[J]. 造纸科学与技术， 2014， 33（6）： 124.

[4] Li Qian， Pang Xiao， Tang Wei， et al. Application of Improved PSO Algorithm in Parameter Setting of Pressure Control in Paper Drying[J]. Paper and Paper Making， 2016， 35（10）： 4.

李 茜， 庞 肖， 汤 伟， 等. 基于改进的PSO算法在纸机干燥部压力控制PID参数整定中的应用.[J]. 纸和造纸， 2016， 35（10）： 4.

[5] Liu Jinkun. MATLAB simulation of advanced PID control[M]. Beijing： Electronics Industry Press， 2004： 233.

刘金琨. 先进PID控制MATLAB仿真[M]. 北京： 电子工业出版社， 2004： 233.

[6] LEE C H， CHANG F K. Fractional-order PID Controller Optimization via Improved Electromagnetism-like Algorithm[J]. Expert Systems with Applications， 2010， 37（12）： 8871.

[7] Li Rui. Research on Steam and Condensate Thermo-Dynamic System Based on Adjustable Thermal Compressor[D]. Xian： Shaanxi University of Science & Technology， 2012.

李 蕊. 基于可调热泵的蒸汽冷凝水热力系统研究[D]. 西安： 陕西科技大学， 2012.

[8] Wang Xianfang， Du Zhiyong， Pan Feng. Tuning PID parameters based on chaotic immune genetic algorithms[J]. Computer Engineering and Applications， 2010， 46（13）： 242.

王鲜芳， 杜志勇， 潘 丰. 基于混沌免疫遗传算法整定PID参数[J]. 计算机工程与应用， 2010， 46（13）： 242.

[9] Zhang Jiajun. Optimization Parameters of PID Controller Parameters Based on Particle Swarm Optimization[J]. Computer Simulation， 2010， 27（10）： 191.

张家骏. 基于粒子群算法的PID控制器参数优化研究[J]. 计算机仿真， 2010， 27（10）： 191.

[10] Wang Xiaoping， Cao Liming. Genetic algorithm—theory， application and software implementation[M]. Xian： Xian Jiaotong University Press， 2002： 15.

王小平， 曹立明. 遗传算法——理论、应用与软件实现[M]. 西安： 西安交通大学出版社， 2002： 15.

Application of the PID Parameters Optimization Based on Improved Genetic

Algorithm in Blow-through Steam Flow Rate Control

TANG Wei1 YANG Runshan1，*SUN Zhenyu2

（1College of Electrical and Information Engineering， Shaanxi University of Science and Technology， Xian， Shaanxi Province， 710021;

2College of Mechanical and Electrical Engineering， Shaanxi University of Science and Technology， Xian， Shaanxi Province， 710021）

（*E-mail： 576984316@qq.com）[JZ）]

Abstract：Blow-through steam flow rate control of paper machine dryer section is an important measure to solve the problem of hydrops in the steam dryerBlow-through steam flow rate control usually uses PID controller，while traditional PID control is usually inaccurate and the parameters setting method is time consuming， its difficult to achieve the ideal control effectIn this paper， on the basis of the analysis of basic genetic algorithm，an improved genetic algorithm was put foward， the algorithm was used in PID controller parameters optimization， which implemented the accurate control of blow-through steam flow rate control of paper machine dryer sectionMATLAB simulation experiments showed that the proposed control system had the characteristics of faster response speed， smaller overshoot and better robustness compared with the conventional PID controller and PID controller based on basic genetic algorithm， it could achieve the ideal control effect， the practical application of this algorithm significantly increased the utilization efficiency of secondary steam， which obtained the prominent economic benefits.

Keywords：blow-through steam flow; genetic algorithm; PID control parameters optimization; dryer sectron