考虑止水位置的平面钢闸门应力有限元分析
杨光明 万宇飞 俞人杰 蔡俊鹏


摘要:目前关于闸门止水系统布置在上游面还是下游面,一般全凭经验决定,缺少数据支撑。以某水利工程平面钢闸门为实例建立有限元模型,应用ANSYS软件对比前、后两种止水方式下平面闸门各构件的应力分布及主横梁的挠度变形。结果表明:闸门构件应力满足强度要求,部分小范围内存在应力集中现象;采用后止水时闸门面板应力分布均匀,主横梁抗变形能力强,且边梁的最大折算应力值较小,其它构件在两种止水方式下的静力特性无显著差异。分析成果可为类似工程止水布置以及闸门设计提供参考。
关 键 词:止水方式; 应力分布; 变形量; 有限元; 平面钢闸门
中图法分类号:TV663 文献标志码: ADOI:10.16232/j.cnki.1001-4179.2019.01.028
水工钢闸门是用于关闭和开放泄水通道的控制设施,是水工建筑物的重要组成部分。闸门根据结构形状可分为平面闸门、弧形闸门和人字闸门等。其中平面闸门因其结构简单,互换性强、对启闭设备适应性好等优点,在现有工程设施中采用量居于首位[1-2]。
为防止平面闸门与门槽埋件缝隙处漏水,一般要在门叶或埋件上布置止水系统。露顶闸门设置侧止水和底止水;潜孔式闸门兼有顶止水;高孔口闸门还需在分段闸门间设节间止水。止水材料主要是不同断面形状的橡皮。布置形式分为两种;止水材料布置在闸门的上游面,称为前止水式;布置在下游面,称为后止水式[3]。
事实上,关于平面闸门止水系统布置在上游面还是下游面的研究较少,只是依据一般经验。根据前人实践,露顶闸门及一般轮式支承为了避免滑轮与轴承腐蚀,止水系统设置在上游[4-6];需利用顶部水柱压力下落的闸门,以深孔闸门为例,摩阻力较大,止水系统宜布置在下游[7-8]。P.埃比斯蒂等提出大部分电站事故闸门止水设置在上游面是因其价格低廉,对启门力要求容量低,但就安全性而言,设置在下游更有利[9]。目前国、内外闸门设计中,一般未考量止水布置形式对平面闸门自身构件受力影响及变形作用。故本文以某平面闸门为例建立三维模型,借助ANSYS软件在前、后两种止水方式下对平面钢闸门进行静力特性分析,为平面闸门优化设计及止水布置形式提供参考。
1 建模方法及模型离散
1.1 平面闸门建模方法
平面钢闸门是复杂的大型空间薄壁结构体系,由面板、主横梁、水平次梁、纵梁和滑轮等组成。目前,主流设计方法是以结构力学为基础的平面体系法,该方法对结构构件逐个计算,但只限于平面内,不能反映空间结构真实受力。保守设计使得真实数据大于计算结果的20%~40%,部分关键区域易出现安全裕度不够的弊端。随着计算机硬件水平日益成熟和结构力学分析理论的完善,空间有限元法逐渐引入到复杂平面钢闸门结构设计中[10-11]。
平面闸门有限元分析时,空间有限元建模方法又分为板梁组合结构、部分空间薄壁结构、完整空间薄壁结构3类。其中,板梁组合结构建模时对各构件模拟精细程度低,简化方式粗略;部分空间薄壁结构建模时增选了杆单元与梁单元模拟,提高了精细程度;完整空间薄壁结构最贴近现实闸门的工作情况,它将闸门各构件用板壳单元进行离散,模拟出的闸门精确度高,可靠性强[12-13]。本文采用第3种建模方法。
1.2 模型離散
模型离散作为有限元计算工作的基础,可分为单元类型选择与网格划分两部分。基于平面闸门的结构特点与受力方式,面板、主横梁、小横梁、纵梁以及边梁采用壳单元,用shell63来模拟,滑轮采用实体单元,用solid45表示[14]。
由于单元形态决定计算结果,网格划分时应遵循结构规整,各构件连接处有相同节点的原则,以保证良好的变形和协调性。同时,如果单元尺寸过小,会增加分析难度;过大则容易导致误差超出控制范围,不能真实反映结构局部应力和变形结果[15-17],可以通过多次划分比较,进而取得理想的离散模型。
2 工程实例
2.1 工程概况与材料参数
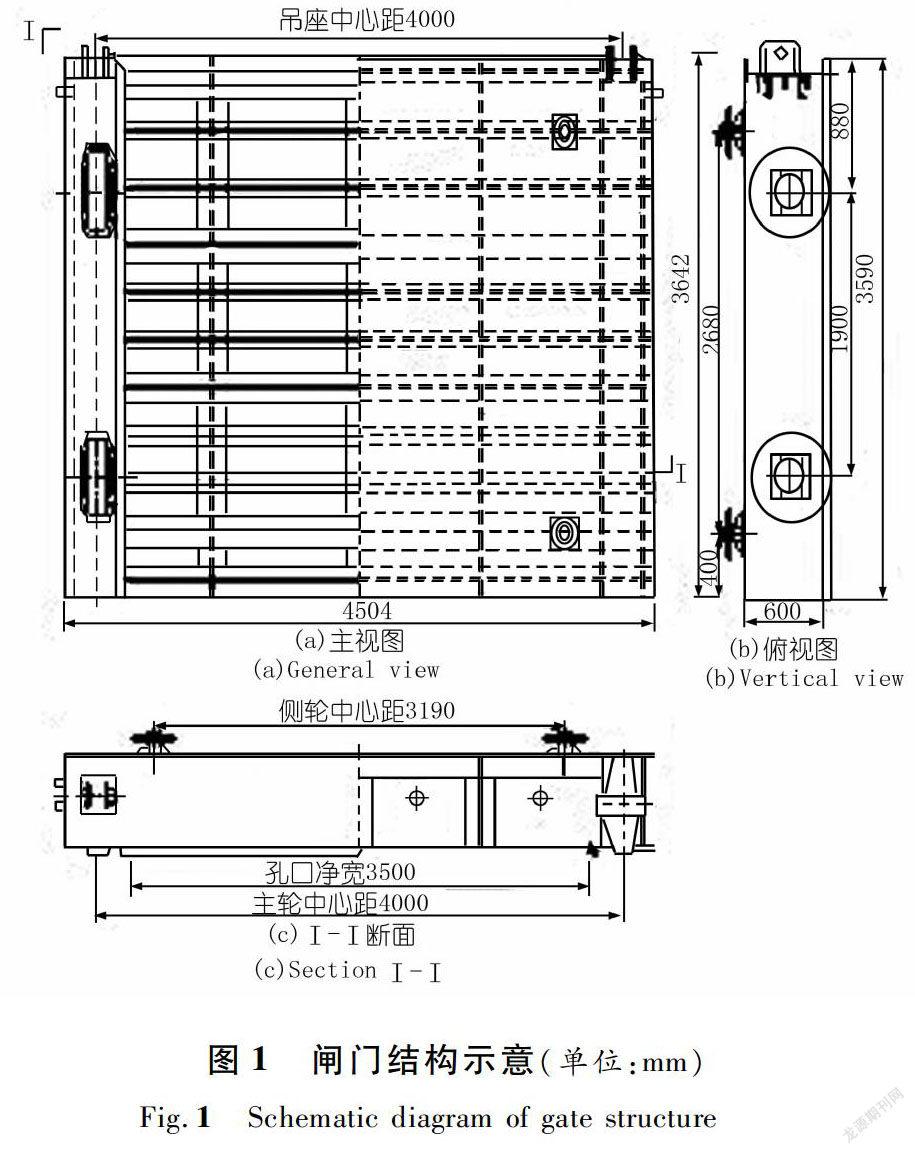
以某泄洪洞事故闸门(潜孔式平面定轮钢闸门)为背景,对不同止水布置下闸门的静力特性进行分析。闸门孔口尺寸3.50 m×3.50 m,闸门尺寸4.50 m× 3.59m(宽×高),梁的计算跨度4.20 m,板梁结构,采用等高布置。主横梁为工字型组合梁,由上至下编号为1~4号;纵梁为T形截面组合梁,从左至右编号为1~3号;边梁为Π形截面组合梁,从左至右编号为1~2号;小横梁为14号工字型钢,共6根从上至下编号为1~6号。
材料采用Q235钢。弹性模量E = 2.06×105MPa,泊松比υ = 0.3,密度ρ = 7.85×103kg/m3。闸门结构如图1所示。
2.2 有限元模型
为得到平面闸门在两种止水方式下闭门挡水工况的工作特性,在建立同一个有限元模型的基础上加设止水封条,分别设置在上、下游面。坐标系定义如下:以闸门主横梁轴向为x方向,铅直方向为y方向,顺水流方向为z方向。滑轮块选用实体单元solid45,其余构件采用壳单元shell63,网格尺寸均选用50 mm,划分单元总数为27 420,节点总数为16 804。平面闸门有限元模型如图2所示。
2.3 边界约束条件
由于闸门结构左右对称,故本文建模时采用对称建模,并在模型对称轴上施加对称约束,闸门滚轮支承在水流方向受到约束,闸门底端施加y方向的竖直约束来限制闸门在竖直方向上地移动。为了保持模型的几何性不变,假定模型底部面板的中间节点在闸门宽度方向位移为零。
2.4 计算工况与荷载
(1) 计算工况。底槛高程576.4 m,设计水头 25.0m。
(2) 荷载。现实运行工作中,闸门受力情况复杂,有水压力、重力、波浪压力、泥沙压力等,此处施加荷载只考虑闸门自重及静水压力的作用[19]。前止水式平面钢闸门受水压力面为面板,后止水平面钢闸门的受水压力面相对复杂,包括顶梁腹板、面板、边梁腹板等。前、后止水式钢闸门受水压力的荷载面(右半部分)如图3所示。
2.5 强度校核标准
钢材Q235(16 mm)的屈服极限为235 MPa,抗拉、抗压、抗弯容许应力为215 MPa,抗剪容许应力为125 MPa[18]。根据《水利水电工程钢结构设计规范》(SL74-2013)中的规条,闸门容许应力应乘以0.90~0.95的调整系数,按《水利水电工程金属结构报废标准》(SL226-98)进行强度验算时,还要乘以0.90~0.95的使用年限修正系数[19-20]。本文系数均取0.92,容许应力修正系数 k =0.85,调整后的抗拉、抗压、抗弯容许应力与抗剪容许应力分别为183 MPa和106 MPa。
当面板边长比 b/a大于1.5时,验算面板的折算应力σ zh 应小于1.1α[σ],α 为弹塑性调整系数,在此取1.5。
在最大弯矩作用面上,剪应力与弯应力的共同作用会使塑性铰提早出现,应以折算应力是否小于屈服极限来判断钢材是否达到塑性状态。
3 有限元静力特性分析
3.1 结构应力计算结果分析对比
3.1.1 面 板
两种止水方式下,边梁之间的面板区域应力分布比较相似,区别主要在边梁附近面域。在前止水式下,面板与边梁内腹板的连接处兼与1,2,5,6号小横梁相交处,面板存在部分应力集中现象;而在后止水式下,面板应力分布均匀,优于前止水式。面板最大折算应力σ zh (最大等效应力)如表1所示。
3.1.2 主横梁
(1) 主横梁腹板。① 前止水式,1号主横梁腹板应力分布中间小,两头大;后止水式,应力分布较为分散,但相应位置应力值远大于前止水式。② 2~4号主横梁腹板应力在两种止水方式下区别不大,都是中间小,两头大。
(2) 主横梁后翼缘。两种止水方式下,后翼缘折算应力分布相似,中间大,两头小。主横梁最大折算应力对比如表2所示。
如表2所示:1号主横梁前止水式腹板最大折算应力值σ zh 为76MPa;后止水式最大折算应力σ zh 为188 MPa,发生在主横梁腹板接近前翼缘区域,比采用前止水式大147%。这是由于后止水式1号主横梁直接受水压作用,应力值普遍远远大于前止水,但最大折算应力仍小于屈服强度,满足强度条件。2~4号主横梁前止水式最大折算应力均出现在闸门跨中接近前翼缘处;而后止水式2~4号主横梁最大应力出现在腹板、后翼缘、边梁腹板三者交界处。
两种止水方式下,后翼缘最大折算应力处于自翼缘中间。前止水翼缘折算应力普遍大于后止水式,只有1号主横梁翼缘出现反常,数值为76 MPa,小于后止水式的84 MPa。这也是由于采用后止水时1号主横梁直接承受水压、受力复杂的关系。
3.1.3 縱 梁
模型中1,3号纵梁对称,故只分析2号和3号纵梁。
(1) 梁腹板。两种止水方式下,纵梁腹板应力分布几无差别,1,3号纵梁应力比2号纵梁稍大。
(2) 纵梁后翼缘。两种止水方式下后翼缘应力分布也类似,都在纵梁与小横梁交界处应力较大。
纵梁最大应力对比如表3所示,表中还列出了腹板正应力σ,剪应力τ,后翼缘正应力σ,由于后翼缘剪应力很小,对闸门整体性状影响较小,故不作分析。
如表3所示,纵梁腹板最大折算应力在前、后止水下数值一致,都是67 MPa。后翼缘最大折算应力分别为22 MPa和18 MPa。可见止水方式对纵梁最大应力影响不大。
3.1.4 边 梁
由于模型对称,故只需分析2号边梁受力即可。
(1) 边梁腹板。两种止水方式下,边梁内腹板应力都普遍比外腹板大,由于边梁荷载面在两种方式下区别较大,其应力分布影响区别较大。
(2) 边梁后翼缘。两种止水方式下,应力分布相似,由于定轮缺口的存在均产生了局部集中应力。
为了准确描述应力分布,将2号边梁腹板划分为8个区域,其示意图如图4所示。
图4 边梁腹板应力分布区域划分 Fig.4 Division for force distribution area of edge beam web
边梁最大应力对比如表4所示,各项应力表示方法与纵梁一致。
内腹板的应力分布差别主要在1,3,4区域。采用前止水时,由于定轮的存在1、3区域在边梁腹板与轮轴交接处,产生应力集中现象,应力最大值为155 MPa;采用后止水式时,1,3,4区域直接承受水压,应力值普遍较大,而区域2由于边梁腹板与轮轴交接处有加强板的存在,应力值偏小。外腹板的应力分布差别主要在区域6及附近小区域。在前止水方式下,该区域不承受水压力,也无应力集中现象,所以应力值较小,为13 MPa;而采用后止水式时区域6直接承受水压力和其它结构承重传递力,导致应力值较大,为116 MPa。腹板最大折算应力后止水式比前止水式小25%。
由于断面缺口,边梁翼缘均在定轮处出现应力集中现象,前、后止水式最大折算应力分别为79 MPa和99 MPa,未超出容许应力。
3.1.5 小横梁
止水的布置形式对小横梁影响较小。小横梁最大折算应力如表5所示。
如表5所示,除1号小横梁最大折算应力值偏小外,其余小横梁最大折算应力相差不大。前止水方式下,平面钢闸门小横梁最大折算应力值σ zh 为126MPa;后止水方式下,平面钢闸门小横梁最大折算应力值σ zh 为128 MPa。最大应力都出现在2号小横梁腹板与后翼缘连接处区域,满足强度校核标准。
3.2 变形计算结果对比分析
主横梁是钢闸门的主要受力构件,假如水工钢闸门的主梁变形超过限定值,钢板由平面变成曲面,两侧门槽止水即失去效果,闸门起吊也会比较困难,故分析给出4根主梁的计算结果。主横梁最大挠度变形如表6所示。
总体而言,后止水式主横梁挠度变形要小于前止水式。前止水方式下,1~4号主横梁的挠度最大变形量逐渐增大;在后止水方式下,2~4号主横梁的最大挠度变形量也逐步增大,其中,1号主横梁的最大挠度变形量大于其它主横梁,且大于前止水式。
如表6所示,前止水方式下,平面钢闸门主横梁最大挠度变形量为3.15 mm,最大变形出现在4号主横梁跨中区域;后止水方式下,平面钢闸门主横梁最大挠度变形量为2.63 mm,最大变形出现在1号主横梁腹板介于3号纵梁与2号边梁内腹板之间区域。前止水式比后止水主横梁最大挠度变形量大19.8%。针对潜孔式闸门,主横梁容许最大挠度不超过主横梁跨度的1/750。两者都没有超过设计要求的5.6 mm。
4 结 语
计算表明,平面闸门在前/后两种止水方式下,闸门各构件都满足强度要求,但在一些构件相交区域及定轮处容易发生局部应力集中,针对这些区域,在不同止水布置下可以进行加固处理。
总体而言,止水方式对纵梁、小横梁影响很小。当潜孔式平面钢闸门采用后止水时面板受力均匀,无应力集中现象;主横梁抗变形效果更强;边梁最大折算应力值比采用前止水式小25%。值得注意的是:当采用后止水布置,由于1号主横梁与边梁腹板直接承受水压力作用,故在设计上主横梁可采用变截面梁,或在面板与主横梁连接处设角钢的方式,而边梁采用加设隔板等方法,可以使闸门应力分布更加合理。
参考文献:
[1]陈五一,欧珠华,刘礼华.水工钢闸门检测理论与实践[M].武汉:武汉大学出版社,2008.
[2]燕怒,孙宜华.金属结构设计[M].武汉:华中科技大学出版社,2012.
[3]刘细龙,陈福荣.闸门与启闭设备[M].北京:中国水利水电出版社,2002.
[4]李建波.平板钢闸门止水问题的探讨[J].山西水利科技,2003(2):49-50.
[5]林庚.平面闸门双向止水的设计选择[J].水利科技,2009(2):34-36.
[6]王晶.平面钢闸门几种双向止水形式设计探析[C]∥山东水利学会第九届优秀学术论文集,2004.
[7]唐红海.小浪底电站闸门止水的设计特点与问题探讨[J].人民长江,2007,38(4):107-109.
[8]刘吉康.一种水电站平板式尾水闸门漏水封堵装置的研究与应用[J].科技创新导报,2017,29(14):106-107.
[9]P.埃比斯蒂,李季川.进水口事故闸门上游止水和下游止水方案比较[J].水利水电快报,2003(8):1-3.
[10]武敏,谢龙汉.ANSYS Workbench 有限元分析及仿真[M].北京:电子工业出版社,2014.
[11]孙琳.平面定轮闸门三维有限元分析[J].水利规划与设计,2013(5):37-40.
[12]谢智雄,周建方.大型弧形闸门静力特性有限元分析[J].水利电力机械,2006,28(4):21-24.
[13]郑圣义,倪尉翔,季薇.不同吊点位置的弧形闸门应力有限元分析[J].人民黄河,2015,37(9):102-105.
[14]冀芳,李岗.基于ANSYS软件的弧形钢闸门三维有限元分析[J].制造业自动化,2015(6):39-41.
[15]雒翠.ANSYS在平面钢闸门三维有限元分析中的应用[J].中国水运,2008,8(5):104-105.
[16]纪伟,任玉珊.基于有限元法的平面鋼闸门结构整体性优化设计[J].人民珠江,2015(3):76-81.
[17]赵营.双悬臂钢叠梁闸门静动力学有限元分析[D].邯郸:河北工程大学,2017.
[18]GB50017-2003 钢结构设计规范[S].北京:中国计划出版社,2003.
[19]SL-2013 水利水电工程钢闸门设计规范[S].北京:中国水利水电出版社,2013.
[20]SL226-98 水利水电工程金属结构报废标准[S].北京:中国水利水电出版社,1999.
引用本文:杨光明,万宇飞,俞人杰,蔡俊鹏.考虑止水位置的平面钢闸门应力有限元分析[J].人民长江,2019,50(1):153-157.
Finite element analysis of plane steel gate stress considering two different water seal positions
YANG Guangming1, WAN Yufei1, YU Renjie2, CAI Junpeng1
(1. College of Energy and Electric Engineering, Hohai University, Nanjing 211100, China; 2. Zhejiang Institute of Hydraulics & Estuary, Hangzhou 310020, China)
Abstract:Arranging water seal on the upstream or downstream side of the gate is usually decided by designers′ experience but without data support. In this paper, the finite element model of plane steel gate of a water conservancy project was established. Considering different water seal positions, the stress distribution of the gate members and deflection of main beam were compared by ANSYS software. The results showed that the stress of the gate member can meet the strength requirement, and the stress concentration existed in a small range. When water seal was arranged on the downstream side of the gate, the stress distribution of the gate face plate was more uniform, the deformation resistance of the main beam was strong, and the maximum converted stress value of the side beam was small. There was no significant difference in the static characteristics of the other members in the two water seal positions.
Key words: water seal layout; stress distribution; deflection; finite element; plane steel gate

