概率公理化方法及其对高中概率教学的启示

摘 要：概率公理化方法是研究概率的重要思想方法，如何正确认识它，不仅对概率论这门学科的自身发展提供坚实的基础，而且对于高中概率教学也有所帮助.笔者在对概率公理化方法的发展历史进行回顾的基础上，论述了公理化方法的意义，分析现在高中概率教学所出现的相关问题，并据此探讨了概率公理化方法对高中概率教学的启示.

关键词：概率论;高中概率;问题;启示

一、概率论公理化的提出

概率论起源于博弈问题[1].15至16世纪意大利数学家帕乔利、塔塔利亚和卡尔丹的著作中曾讨论过“如果两人赌博提前结束，该如何分配赌金”等概率问题，但是到了19世纪，由于获得新的研究动机以及分析方法的引入，使得概率论获得了重要进展.可是在發展过程中，历史上出现了对概率的各种认识，既有实体概率——概率局限于实在的物质世界，也有主观概率——反映了人们对某些事物的一种信任程度，是对事物的不确定性的一种主观判断[2].因此概率论没能演绎成一门逻辑上完美的数学学科，它的基础存在着缺陷，具体将有以下几点：

1、概率论的分析方法本身没有严格化

2、人们对概率这一基本概念的认识不明确

3、频率和概率的认识模糊

上述这些概率的局限使得那时的人们对当时的概率论中的一些概念和方法产生了疑问，认为概率论不是一门合理的科学.于是，数学家们逐步探讨解决的办法，而数学家们总结出的解决办法就是完善概率论自身的理论基础.于是，1900年希尔伯特在巴黎国际数学家大会上所作的著名的报告中的第6问题，就呼吁把概率论公理化[3].由此，概率论公理化正式登上历史的舞台，并将概率论逐步变成一门严谨的科学.

二、概率论公理化的发展

最早对概率论进行严格化尝试的是俄国数学家伯恩斯坦（ C.H.Bernstein，1880-1968）和奥地利数学家米泽斯（R.vonMises，1883-1953 ）.他假定我们在自然科学中的推理是基于以往的经验，只要给定的条件集合α实现，属于已知类A的一个事件必然发生，这和其他因素无关.然而，一般而言，一个事件不可能绝对出现.人们不能完全确切地预言真实现象的行为.只有当条件集合α不太大，而且易于观测时，把α和A联系起来的规律才有实际意义.如果这个条件不成立，事件A就叫做随机事件.然后他试着引进一个简单点的条件集合β来代替α，它（至少在理论上）可以重复实现无限多次，当β存在时，给定试验中事件A以一个明确的概率发生，而且这个概率可以用数值表示.如果也定义了事件B的概率，那么下面三个关系必有一个成立：

然后，伯恩斯坦引进了三个公理：（1）概率的可比较性公理;（2）不相容事件公理;（3）事件组合公理.前两个公理考虑了条件集合β固定的情况.第三个公理把条件α下A的概率与不同的条件集合β下同一个事件的概率联系起来[4].

在1933年，原苏联数学家柯尔莫戈洛夫以德文出版了他的经典性著作《概率论基础》.这本书中建立起了集合测度与事件概率的类比，积分与数学期望的类比，函数正交性与随机变量独立性的类比等等.这种广泛的类比终于赋予了概率论以演绎数学的特征[5].

以下是概率论公理化定义：

设随机实验E的样本空间为Ω.若按照某种方法，对E的每一事件A赋于一个实数P（A），且满足以下公理：

（1）非负性：P（A）≥0;

（2）规范性：P（Ω）=1;

（3）可列（完全）可加性：对于两两互不相容的可列无穷多个事件A1，A2，……，An，……，有

则称实数P（A）为事件A的概率[6].

至此概率论就从半物理性质的科学变成严格的数学分支，和所有其他数学分支一样建立在同样的逻辑基础之上[7].

三、概率论公理化方法的意义

一是概率公理化方法具有分析、总结概率知识的作用.众所周知当一门科学积累了相当丰富的经验知识，需要按照逻辑顺序加以综合整理，使之条理化、系统化，上升到理性认识的时候，公理化方法便是一种有效的手段.如几何学的历史发展，便经历了一个公理化的过程.

二是概率公理化方法不但对建立概率论理论体系，训练人的逻辑推理能力，系统地传授概率知识，以及推广概率理论的应用等方面起到有益的作用，而且对于进一步发展概率理论也有独特的作用.例如在描述概率方面，在概率公理化概念提出以后，人们在对于概率的古典定义、几何定义、频率定义和主观定义时，不像以前都只能在一定的场合下才能给出各自的确定概率的方法，现在就能给出准确的概率定义.

三是概率公理化方法在科学方法论上具有示范作用.任何一门科学都不仅仅是搜集资料，也决不是一大堆事实及材料的简单积累，而都是有其自身的出发点和符合一定规则的逻辑体系.概率公理化方法对现代概率论及现实生活中的实际问题都起到了积极的借鉴作用.在日常生活中，概率公理化的应用也深入其中，例如车站的设立、天桥的设立以及评估产品质量等等.

四是概率公理化方法在形式上所显现出的简洁性、条理性以及结构的和谐性确实符合美学上的要求，因而为数学活动中贯彻审美原则提供了范例.学生在参与学习概率公理化方法的活动中，不仅要让他们接受美的熏陶，从中陶冶性格，丰富精神生活.

四、高中概率教学

4.1高中概率教学的内容

以普通高中数学课程标准实验教科书人教A版为例，高中阶段学习的概率知识总体概括一下可以分为以下两个部分：

第一部分为必修部分：概率的定义，频率与概率的区别，互斥事件与对立事件的区别，加法公式与乘法公式，古典概型，几何概型，随机数的产生，随机模拟方法估计概率.

第二部分选修部分：分步计数原理，排列与组合，二项式定理概率，超几何分布，二项分布，离散型随机变量的期望、方差.

4.2 高中概率教学中存在的问题

在知网当中，通过对“概率教学问题”进行文献检索，共检索出247篇相关文献，其中硕士论文为27篇，期刊为220篇.对其中提出的概率教学中存在的问题进行总结，大致可以分为：教师问题、学生问题、教材问题三个方面.现总结如下：

4.2.1 教师中存在的问题

一是教师对概率和假设逻辑检验观念不明确

在实际教学中，由于教师对概率论公理化的方法认识不清，无法明确概率论中无异现象与假设逻辑检验观念，并且很多教师对假设逻辑检验理解不深刻，缺乏统计概率的观念，仅是主观的想法，缺乏对学生客观想法的认识.

二是过多采用排列组合来计算概率

大部分的教师还利用课程改革以前的授课模式，先讲排列组合，再讲古典概型，通过求解样本空间总数来求概率，这样使许多学生产生了固定思维方式，即求概率就是用排列组合求样本空间，而忽略对随机思想的理解，也缺乏对概率公理化的认识，也就是单纯的应试教育思想，没能真正实现向素质教育思想的转化.

三是对学生错误的概率的认识缺乏深入解释

由于教师本身对概率的随机性研究不够深刻，也不能很好地向学生解释随机事件发生的不确定性与频率相对稳定性的重要性，从而使学生对随机事件产生错误的认识，而这种认识将使得他们在解决问题过程当中无法很好地运用所学过的概率论知识去解答，凭借自己的主动思维去解决问题.

四是对概率知识结构体系不够明确

由于个别教师对概率论公理化的形成与发展不够熟悉，又只是按照课本设计的内容进行教学，这就使得学生在学习概率知识时，弄不弄清楚来龙去脉，对概率知识没有一个系统的了解，概率知识比较零散，这样也会使得学生在遇到问题时，不知道该怎么求解，从而造成学生的学习障碍.

4.2.2 学生中存在的问题

一是对随机概念的理解存在问题

由于学生对不清楚概率的由来，所以往往在处理随机问题时以主观代替客观，常常以公平、可能性等词语来表达随机的意思，不能正确理解随机事件的不确定性与频率发生的稳定性，从而在解决问题中产生错误的想法.

二是对概率当中为0和1的事件理解不够准确

“概率为零的事件一定为不可能事件，概率为一的事件一定是必然事件”，这是在实际调查当中所遇到的最多的错误认识，不可能事件概率一定为零，必然事件的概率一定为一，反之并不一定成立，我们不妨通过这样去理解：比如一颗豆子掉在操场的某处A，由于坐标是某一个点A，而全集是一个面积，所以概率就为零，但并非不可能事件.还有比如一个点随机落在一个圆中，这个点落不到圆心的概率为：出去圆心外圆的面积比上整个圆的面积等于1，但是这个点有可能刚好落在圆心，并且概率为零.

三是在随机事件中，对基本事件的取法唯一

在学习过程中，学生对基本事件当中“基本”的含义理解不深刻，基本二字是针对具体的实验要求与目标而言的，而不是具体不变的，任何一个事件按不同的要求都可以划分为不同的基本事件，这也是概率论公理化所解释的问题之一，然而学生在刚学习基本事件这一概念的时候，由于对概率论公理化不够了解，解题的思路又有所局限，加之教师没有讲解公理化的由来，就会使得学生认为选取基本事件是唯一不变的.

四是混用概率当中的加法与乘法公式

相互独立事件与互斥事件是是学生最容易搞混的知识点之一，由于对公理化的描述不够重视，理解不够深入，学生极易将两者混淆，因此学生在解决问题时一味的套用公式计算去判断或者凭借自己的主观想法去判断.

五是忽略条件概率

在计算概率时，学生最容易忽略的一个问题就是审题不清，在题目中往往设置陷阱——条件概率.条件概率是指事件A在另外一个事件B已经发生条件下的发生概率.条件概率表示为：，读作 “在B条件下A的概率”.（条件概率就是概率公理化的形成公式之一）例如：一对夫妻有两个小孩，已知其中一个是女孩，则另一个是女孩子的概率是多少？解：，夫妻有两个小孩，那么它的样本空间为女女，男女，女男，男男，则为1/4，=1-=3/4，所以最后等于1/3.

4.2.3 课程本身的缺陷

虽然在新课程改革后对课程标准对概率的要求进行了修改和完善，但是具体的要求还是比较抽象，缺乏具体的教学指导，例如在新课程中要求教师对概率教学要重视概率的实际应用，要求学生在实践中明白概率的思想及教育价值，但是首先在课程中并没有安排具体的课时，其次在课本中也没有有关概率思想这一内容作为补充，所以就会导致许多老师不重视概率论的形成与发展，依然保持着讲概念再练题的模式.

通过对上述三个方面存在的问题进行总结概括可以发现，绝大部分的问题都是出现在对于概率相关概念认识不清所造成的，又由于概率公理化的意义就在于理清概率的相关概念，所以在此基础上笔者认为利用概率公理化的方法对概率相关概念进行解释，可以有效解决有关概念不清所导致的问题，让教师和学生能够更好地进行概率的教与学.

五、概率论公理化对高中概率教学的启示

5.1 对教师的启示

随着课程的不断改革，教师也需要改变传统的概率教学观念，明确概率教学的目标与要求，着重培养学生公理化思想.在此针对高中概率教学中存在的误区，给出了以下建议：

一是加强概念的教学，并在其中引公理化的思想

高中概率的学习其本身就存在抽象性，除此之外概率的概念也不容易理解，所以这一点上让很多学生和老师头疼，所以教师更应该加强概率论中有关概念的学习，对概念进行新的诠释，让学生能够更好地理解以及应用.概念的充分理解是学生处理概率问题的基础，同时也对养成好的学习习惯起了铺垫作用，所以教师应该在上课过程中详细的向学生解释概率论中相关概念的意义.比如：必然事件、不可能事件、互斥事件、对立事件等等，但是如何更好地解释相关概念呢？在此，教师可以利用概率公理化的思想，利用学生已熟知的公理，去理解相关概念.例如：理解必然事件的概率为1.就可以利用公理化的思想進行转换，设随机实验E的样本空间为Ω，则P（Ω）=1;通过公理化的方法也能够让学生对概念有更深的理解，也能够利用代数的方法解释相关概念，而不是一味的死记硬背.

二是重视知识系统化、全面化

要想让学生对概率知识有深层的理解就必须把知识系统化，而不是零零散散，只有将知识系统化学生才会学着轻松，对整个概率知识结构一目了然.在整理概率的知识系统时，应该讲公理化的方法融入其中，因为概率公理化的形成讲概率变成了一门科学的学科，也正因为有了公理化，概率才有了研究方法，正确的定义.教师决不能抱有概率的学习很简单，概率的发展史考试又不考，只要会做题就可以的心态，教师必须要改变传统的教学模式，学习一个知识就要搞清知识的来龙去脉，这样不能能够提高学生的学习兴趣，而且更能让学生加深对概率的认识，能够更好地运用在实际生活当中.

5.2 对学生的启示

一是整体理解概率，完善认知结构

在概率知识学习的过程中，学生要对自身的知识做出及时的评价和必要的调整.认知结构是学生在认识客观事物和掌握知识的过程中逐步形成的整体结构，是学生的认识活动顺利进行的心理机制，一般来说，它是由教材中的知识结构内化而形成的.概率知识结构是概率学习内容中的基本概念、基本公式、基本观念和基本方法的组织形式和相互联系.学习任何知识，都不能将知识孤立的隔裂开来，尤其是概率知识十分讲究内在逻辑性和整体性，要求学生应该从概率论公理化的发展着手，利用公理化的方法研究概率的相关问题.

二是更多地训练利用概率论公理化的方法解决概率问题

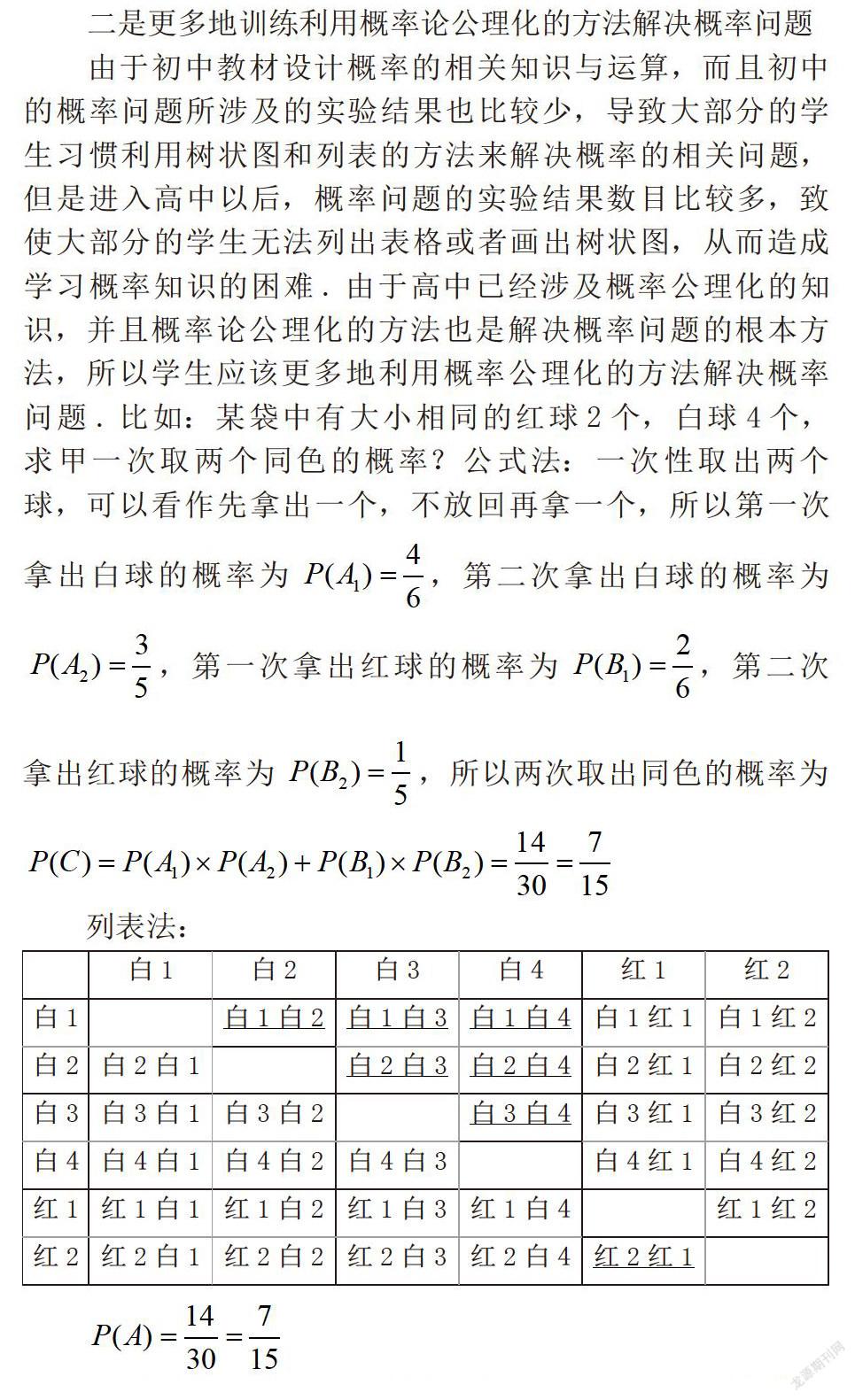
由于初中教材设计概率的相关知识与运算，而且初中的概率问题所涉及的实验结果也比较少，导致大部分的学生习惯利用树状图和列表的方法来解决概率的相关问题，但是进入高中以后，概率问题的实验结果数目比较多，致使大部分的学生无法列出表格或者画出树状图，从而造成学习概率知识的困难.由于高中已经涉及概率公理化的知识，并且概率论公理化的方法也是解决概率问题的根本方法，所以学生应该更多地利用概率公理化的方法解决概率问题.比如：某袋中有大小相同的红球2个，白球4个，求甲一次取两个同色的概率？公式法：一次性取出两个球，可以看作先拿出一个，不放回再拿一个，所以第一次拿出白球的概率为，第二次拿出白球的概率为，第一次拿出红球的概率为，第二次拿出红球的概率为，所以两次取出同色的概率为

通过对上述两个方法进行比较，可以看出公理化的简单明确，列表法虽然可以清楚的看出数量关系，但是如果数据一多就很不容易列表，至此也希望高中学生在解决概率问题时，多利用概率论公理化的方法.

5.3 对教材的启示

教材是学生学习知识的来源之一，教材也是以课程标准为基础，鉴于上述的分析，笔者认为在教材的编写上应该适当增加概率论公理化及其性质推导的部分，可以利用文氏图展现的方式，让学生能够像学习几何那样，能够直观的理解概率公理化的内容与性质，也可以让学生在学习概率知识时有迹可循，在引言中提及概率公理化思想，淡化学生传统的计算思想，多增加一些关于发散思维的趣味知识，增强学生的学习兴趣，缓解课堂氛围，或是多增加一些概率论公理化的史学知识等，让学生亲自去体会概率论公理化的发生和发展过程，逐步提升学生学习概率知识的兴趣和解决概率问题的能力.

参考文献

[1] 徐传胜，吕建荣.亚伯拉罕·棣莫弗的概率思想与正态概率曲线[J].西北大学学报：自然科学版，2006，36（2）：339-343.

[2] 张尧庭，陈汉峰.贝叶斯统计推断[M].北京：科学出版社，1991：230- 231.

[3] Ronald Calinger. Classics of Mathematics[M].New Jersey.  Prentice-Hall，Inc，1995.708.

[4] L.E. Maistrov， Probability theory：a historical sketch[M]，New York，1974，pp.249-252，254-256，261，-262.

[5] 李文林，数学史教程，高等教育出版社，施普林格出版社「M]，2000，p.290.

[6]王明慈，沈恒范 .概率论与数理统计第二版：高等教育出版社 ，2007

[7]程小红，杨静.概率论公理化源头初探[J].西北大学学报（自然科学版），2007（06）：1026-1028.

作者簡介：杜剑南，甘肃兰州人，西北师范大学教育学院硕士研究生，研究方向为：数学教学论.