从三门问题说起

韩学思 邓天择

摘 要：本文从三门问题出发去探究并总结出一些研究问题的方法和角度。

关键词：三门问题

我在看美国的一档电视节目《Let's Makea Deal》时看到了这个三门问题：假如你在参加一个游戏，有三扇门1、2、3：其中有一扇门后面放着一辆汽车，另外两扇门后面是山羊，你会赢得你选择的那扇门后面的礼物。游戏开始时，你任意选择一扇门，假如为门1。主持人从剩余两扇门中选择一扇后面不是汽车的门打开，比如为门3，现在主持人问：为了赢得车，是否要改选门2（另外一扇没有被打开的门）？

首先我们做出如下假设：

现在有三扇门，只有一扇门有汽车，其余两扇门的都是山羊。

汽车事前是等可能地被放置于三扇门的其中一扇后面。

参赛者在三扇门中挑选一扇。他在挑选前并不知道任意一扇门后面是什么，主持人知道每扇门后面有什么。

如果参赛者挑了一扇有山羊的门，主持人必须挑另一扇有山羊的门。

如果参赛者挑了一扇有汽车的门，主持人等可能地在另外两扇有山羊的门中挑一扇门。

那么参赛者现在有两种选择，保持他的原来选择，或者是转而选择剩下的那一扇门。

我们用几种方法来研究这个问题。

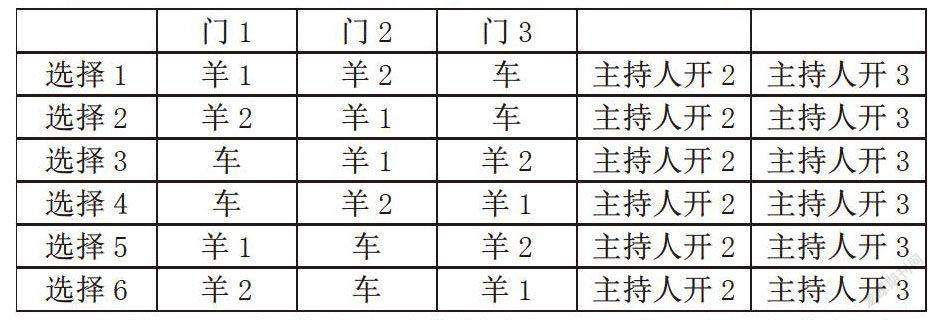
角度1：穷举法

把所有可能的结果列举出来，如下表所示

共有3种情况，如果选择“不换”，其中有一种情况会赢得车，所以赢车的概率为1/3;如果选择换，其中有两种情况会赢得车，所以赢车的概率为2/3。由此，应该换，选择换门后，赢车的概率从1/3提高到2/3.

角度2：理论分析法

有三种可能的情况，全部都有相等的可能性（1/3）︰

参赛者挑山羊一号，主持人挑山羊二号。转换将赢得汽车。

参赛者挑山羊二号，主持人挑山羊一号。转换将赢得汽车。

“参赛者挑汽车，主持人挑羊一号。转换将失败”，和“参赛者挑汽车，主持人挑羊二号。转换将失败。”此情况的可能性为1/3×1/2+1/3×1/2=1/3。

角度3：仿真法

另一种解答是假设你永远都会转换选择，这时赢的唯一可能性就是选一扇没有车的门，因为主持人其后必定会开启另外一扇有山羊的門，消除了转换选择后选到另外一只羊的可能性。因为门的总数是三扇，有山羊的门的总数是两扇，所以转换选择而赢得汽车的概率是2/3，与初次选择时选中有山羊的门的概率一样。

补充说明：

第一次选的空门（概率66.6%），之后主持人开另一个空门，换门，得到汽车;

第一次选的汽车（概率33.3%），之后主持人开另一个空门，不换门，得到汽车;

这里影响到结果的概率问题只发生在第一次选门上，如果条件如上设置，当一开始的门选定后，事件的结果也就决定了，所以这里不存在之后主持人是选择1号空门，还是2号空门的问题，所以在做概率计算是不考虑主持人的选择。如果也要考虑主持人的话：

第一次选的空门1（概率1/3），之后主持人开另一个空门，换门，得到汽车。事件总概率1/3。

第一次选的空门2（概率1/3），之后主持人开另一个空门，换门，得到汽车。事件总概率1/3。

第一次选的汽车（概率1/3），之后主持人开另一个空门1（概率1/2），不换门，得到汽车这个事件总概率1/3×1/2=1/6：

第一次选的汽车（概率1/3），之后主持人开另一个空门2（概率1/2），不换门，得到汽车这个事件总概率1/3×1/2=1/6：

主持人选1号空门还是2号空门打开，这里有个主持人的选择概率，我假设的是主持人随机选择（抽签或者随意），所以各给了50%的概率，如果主持人就是喜欢1号空门，必开1号，那么也就成了1号（100%），2号（0%）了，最后结果并不影响。

所以开始选中汽车，最后换门不得奖的概率是33.3%，开始选中空门，换门最后得奖的概率是66.6%。

角度4：定性分析

或许，3扇门并不利于我们研究这一问题，不妨将3扩大为50，甚至100.当我们选中其中一扇门时，主持人打开了98扇门后没有汽车的门，那么这时候，换与不换其实是很明确的。毕竟，你在一开始就在100扇门中选到有车的门的几率是很小的。

结论：通过以上几种方法的计算，可以明显看出换门得奖的概率更高

在题目设定中，事实上是以“主持人知道哪扇门后面有车”为前提的，此时不妨换一个题目，假设主持人也什么都不知道，只是在你选定一扇门的前提下，再在剩下两扇门中随机打开一扇，而非是直接打开门后为山羊的门，此时题目便会变得异常简单，结果也会与大家所接受的二分之一更为符合。

由此可知，概率的大小实际上与已知信息有很大的关系。在上一个问题中，主持人的“知情”与“智障”使结果有了很大的变化。