浅析游标卡尺的读数策略
陆建成




一、前言
使用刻度尺测量长度时可以精确到毫米,还可以估读到毫米的下一位。但是对于更为精确的测量,刻度尺就显得力不从心了。游标卡尺就是为了弥补刻度尺的不足而制作的。
“能够熟练地运用游标卡尺来进行测量,并能准确读出测量值”是对高中学生掌握游标卡尺的要求,也是高考对基本仪器掌握程度的考查知识点之一。对学生来说,准确地读出测量值是难点。另外,高考同时也考查学生的知识迁移能力,因而对于另类的游标卡尺,也要求学生熟练掌握其读数规律。
二、常见的游标卡尺
对学生来说,常见的游标卡尺主要有以下三种:
第一种主尺的最小分度是1mm,游标尺上有10个小的等分刻度,它们的总长度等于9mm,游标的最小分度就是0.9mm,因此游标尺的每一分度与主尺的最小分度相差0.1mm(即1mm-0.9mm=0.1mm)。
第二种:主尺的最小分度是1mm,游标尺上有20个小的等分刻度,它们的总长度等于19mm,游标的最小分度就是0.95mm,因此游标尺的每一分度与主尺的最小分度相差0.05mm(即1mm-0.95mm=0.05mm)。
第三种:主尺的最小分度是1mm,游标尺上有50个小的等分刻度,它们的总长度等于49mm,游标的最小分度就是0.98mm,因此游标尺的每一分度与主尺的最小分度相差0.02mm(即1mm-0.98mm=0.02mm)。
三、巧记精确度
精确度是很好记的,第一种游标卡尺的精确度是0.1mm,正好是主尺上的1mm除以游标上的10个等分得到的结果。同样的道理,第二种游标卡尺的精确度是;第三种游标卡尺的精确度就是。
四、游标卡尺的读数规则
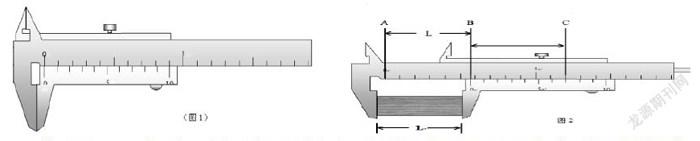
如图1,当游标卡尺的左右测量爪之间没有任何测量物,从而靠在一起的时候,主尺上的0刻度线跟游标尺上的0刻度线对齐;
如图2,当在游标卡尺的左右测量爪之间放上测量物时,左右测量爪拉开了一定的距离L,这个距离L正好等于主尺上的0刻度线跟游标上的0刻度线之间的距离L。
图2中L=AB,AB=AC-BC。这样,我们可以通过“长度相减”得到L的大小。即AB=12mm,BC是游标尺上7格总长度,每格0.9mm,即BC=7×0.9=6.3mm。所以
L=AB=AC-BC=12mm-7×0.9mm=5.7mm
而12mm-7×0.9mm=12mm-7×(1-0.1)mm=12mm-7mm+7×0.1mm=5mm+7×0.1mm
规律:5.7mm中的5mm正好是主尺上的整毫米数;而7×0.1mm中的0.1是就是这种10等分游标卡尺的游标尺精确度,7指的是游标上第7格对准主尺上的某一格。因此,读数规则可以这样构建:读数=主尺上的整毫米数+游标上对齐的第N格×精确度
五、读数的合理性
像图5中的读数,可能会有很多学生读成21.4mm,实际上,准确的读数应该是21.40mm。错误的原因就是没有注意是精确度取到毫米的下两位;也有学生读成21.42mm,这个读数也是错误的,错误的原因就是21.42mm不是0.05的整数倍,实际上,不管正整数N是多少,乘以0.05mm,都不会得到0.42这个数。
因此,10等分的,要读到毫米的下一位,且最后读数应该是0.1的整数倍;20等分,要读到毫米的下两位,且最后读数应该是0.05的整数倍;50等分的也要读到毫米的下两位,且最后读数应该是0.02的整数倍。
六、另类游标卡尺的读数
除了常见的这三种游标卡尺,其实还有一些另类的游标卡尺。
第一种另类:这种游标卡尺的主尺上的最小刻度仍然是毫米,且所标示数以毫米为单位;游标上的格数仍然是10个小格,不过游标上的第10小格与主尺上的19mm对应。如图6所示:
由于该游标卡尺游标上的每一等分都是1.9mm,与主尺上的2mm相差0.1mm。因此,当游标每向右移动0.1mm时,必有一游标上的刻度线与主尺上的某一刻度线对齐。只要找到游标尺上的第几条刻度线与主尺上的刻度线对齐,便知道游标尺移动的距离。因此,它的功能与通常介绍的10分度的游标卡尺相同。不过,由于这种设计使得游标尺上的游标刻度较大,读数时更容易区分游标上的刻度线与主尺上的刻度线对齐与否,减小了出错的可能;同时,该游标卡尺主尺上的标度为毫米,则所读游标的结果可与主尺上的示数直接相加,无需在厘米与毫米之间换算,这同样可以减小因转换单位时可能产生的错误。因此,这种游标卡尺的设计在使用上比前文所说的10分度显得更简单、快捷,也不容易出错。
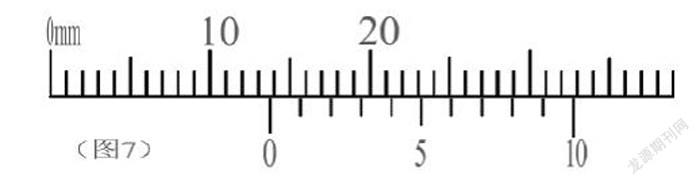
如图7,游标卡尺的读数为13mm+7×0.1mm=13.7mm。
同理,也可以设计出这样的游标卡尺:游标上的格数是20小格,不过游标上的第20小格与主尺上的39mm对应。由于该游标卡尺游标上的每一等分都是1.95mm,与主尺上的2mm相差0.05mm。即精确度仍为0.05mm。
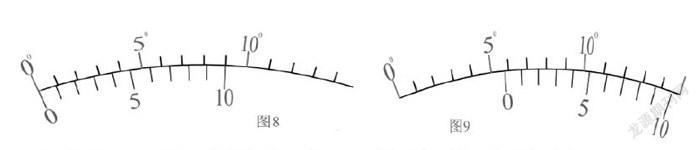
第二种另类:将游标卡尺变形,设计成弧形,用来测量角度。如图8所示:这种游标卡尺主尺上的最小分度为1°,游标上有10个小格,对应的角度为9°,每一小格对应的角度为0.9°。游标尺每順时针旋转0.1°,必有一游标上的刻度线与主尺上的某一刻度线对齐。故这种游标卡尺的精确度为0.1°或者6′。由于其精确度为0.1°或者6′,因而比普通的量角器更为精确。
如图9,此时游标卡尺的读数应该是5.7°,即5°+7×0.1°=5.7°;或者也可以读成5°42′,即5°+7×6′=5°42′。
同理,也可以设计出这样的游标卡尺,如图10:这种游标卡尺主尺上的最小分度也是1°,游标上有30个小格,对应的角度为29°,每一小格对应的角度为(29/30)°。游标尺每顺时针旋转(1-(29/30))°=(1/30)°,必有一游标上的刻度线与主尺上的某一刻度线对齐。故这种游标卡尺的精确度为(1/30)°或者2′。
如图11,此时游标卡尺的读数应该是6°22′,即6°+11×2′=6°22′。
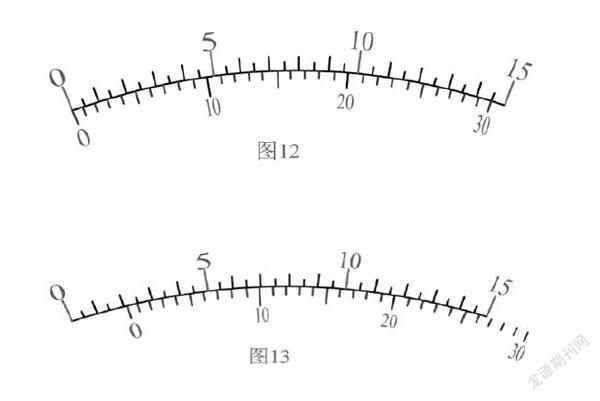
同理,还可以设计出这样的游标卡尺,如图12:不过这种游标卡尺主尺上的最小分度不是1°而是0.5°;游标上有30个小格,对应的角度为14.5°,因此每一小格对应的角度仅仅为(14.5/30)°。游标尺每顺时针旋转(0.5-(14.5/30))°=(0.5/30)°,必有一游标上的刻度线与主尺上的某一刻度线对齐。故这种游标卡尺的精确度为(0.5/30)°或者1′。
如图13,此时游标卡尺的读数应该是2°9′,即2°+9×1′=2°9′。
七、后记
游标卡尺的读数是高中物理的一个教学难点,但笔者认为,只要教案设计得当,教学引导得力,就容易启发学生掌握游标卡尺的原理与读数的规则,则难点不再成为难点。

