钢-混组合连续梁桥徐变性能研究
许小龙 陈强


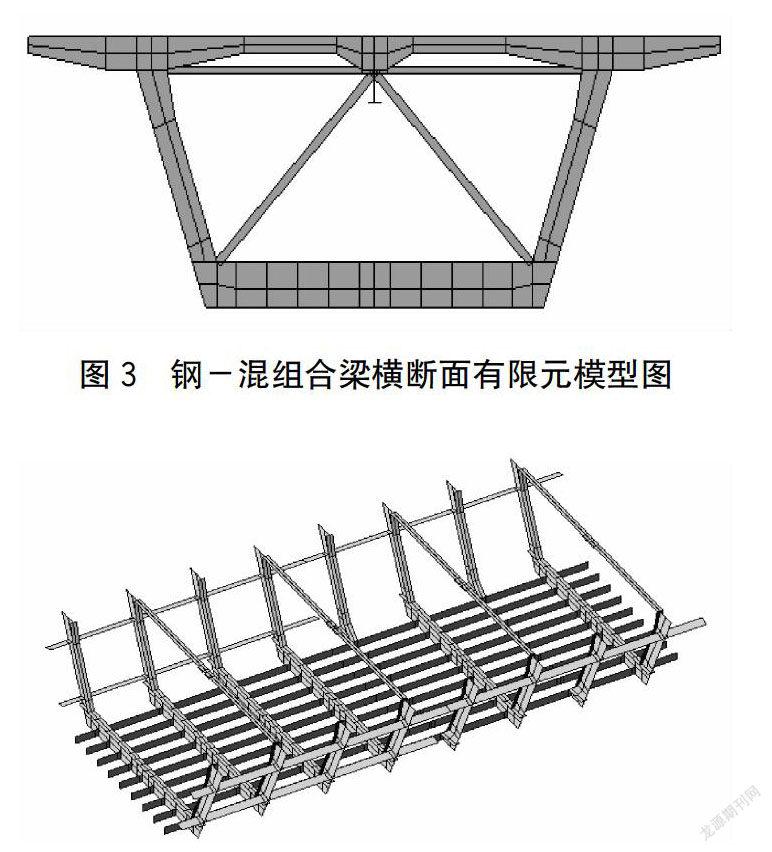

摘要:文章在归纳总结现有徐变效应模型的基础上,确定适用于钢-混组合连续梁桥的徐变预测模型为JTG 3362-2018徐变预测模型,并以某海洋环境中的6x 85m钢一混组合连续梁桥为研究对象,通过精细化有限元分析软件Midas Civil建立了6x 85m钢一混组合连续梁桥全桥精细化计算模型,分析徐变效应中成桥时间、加载龄期、湿度三种关键因素对钢一混组合连续梁桥长期挠度和应力变化的影响,获得了钢一混组合连续梁长期挠度及应力与成桥时间、加载龄期、湿度之间的对应关系。
关键词:钢-混组合梁桥;徐变效应;预测模型;长期性能;力学性能
中图分类号:U448.215 文献标识码:A DOI:10.13282/j.cnki.wccst.2019.10.024
文章编号:1673-4874(2019)10-0080-05
0引言
钢-混凝土组合梁是通过剪钉连接钢梁和混凝土板而形成的组合结构,在桥梁成桥后,随着时间的推移与环境的变化,混凝土徐变效应会对整体结构产生许多不利影响。同时由于混凝土徐变的存在,也加大了施工的难度,使得梁段难以达到设计标高,给预拱度的合理设置提出难题。对于组合连续梁等超静定结构,由于存在冗余约束,徐变还会在结构内部产生额外内力,导致桥梁结构内力发生重新分布。目前对于徐变的研究,主要是通过试验法以及有限元仿真分析法,得出实际构件的应力变化值以及挠度变形值。钢-混组合桥梁作为一种新桥型,相应的徐变研究较少,而组合梁由于剪力连接键的存在以及钢梁对混凝土板的约束作用,使得其整体结构的内力比一般混凝土梁桥更为复杂,因此,准确分析钢-混组合梁徐变效应对桥梁结构的影响具有非常重要的工程实用价值。
近年来,在徐变领域,众多的国内外学者采用长期试验方法和数值模拟方法开展了系统的研究工作,获得了一批有价值的结论。Erkmen使用ABAQUS软件建立了钢一混组合弯桥的徐变效应有限元分析模型,得出了钢-混组合弯桥的竖向挠度与横向变形随时间变化关系。邱文亮基于有限元分析理论,提出一种简化分析模型,该模型能直接运用于长期荷载下钢-混组合梁桥的徐变研究,获得桥梁关键部位的主要力学性能的长期变化规律。刘永健分析了广东东江大桥混凝土徐变效应对桥面板应力以及跨中挠度的影响,研究结果直接运用于东江大桥。袁明以PC连续梁桥为研究对象,推导出混凝土徐变作用下桥梁的各项力学性能计算公式,研究了混凝土徐变对结构影响的规律,并对混凝土板中预应力束的合理布置提出了建议。
基于上述国内外研究现状,本研究以某海洋环境中的6x 85m钢一混组合连续梁桥为研究对象,通过精细化有限元分析软件Midas Civil建立该桥全桥精细化模型,采用徐变预测模型对组合连续箱梁进行徐变研究,探明钢一混组合连续梁挠度和应力随徐变关键影响因素的变化关系,为桥梁的合理设计和安全施工提供相应的理论指导和技术支撑。
1工程概况与有限元模型
某海洋环境中的6x85m钢一混组合连续梁桥的纵断面示意图如图1所示。钢-混组合连续梁主梁为单箱单室钢结构箱梁,箱梁两侧顶板和小纵梁顶板布置有集束式钢结构剪力钉,剪力钉与其上的C60混凝土板相连,组合成整体。
钢-混组合梁主梁节段示意图如图2所示。单幅单向四车道,双幅共双向八车道。大桥设计使用年限为120年。
选取该桥为徐变效应的研究对象,采用MidasCivil软件建立全桥六孔钢-混组合梁有限元精细化模型,混凝土板由C60混凝土制成,钢梁由Q345QD钢制造。钢主梁、小纵梁、纵横向加劲肋、横隔板由实体单元进行建模,预制混凝土桥面板由实体单元建模,其余构件采用杆系梁单元模拟,6孔组合连续梁全桥共有86984个单元,75636个节点,如图3和图4所示。严格按照设计规定在程序中进行施工阶段的划分与设置,分析桥梁的力学行为。由于本研究中组合连续梁采取先简支后连续的施工丁序,即在支座处划分一个小节段作为简支变连续连接段,先放置施工用临时支座,从而使梁处于简支状态,待相邻节段焊接结束后,钝化施工用临时支座,进而达到简支变连续过程的转换。在Midas Civil软件程序中,在整孔架设阶段使相邻跨的焊接连接段的模型参数为零,不参与结构受力,在焊接完成后给予其模型参数参与结构整体受力。组合梁没拆除临时支座之前,即组合梁桥处于在简支状态下提取支座反力,将此支座反力作用于临时支座处位置,计算得到组合梁实际内力状态。为了给予负弯矩位置处一定的预压力,以避免相应部位混凝土发生裂缝病害,组合梁施工中采用了顶升的施丁工艺。在Midas Civil软件程序中,给支点设置一个向上的位移300mm来模拟对混凝土板支点处的顶升。
2 徐变预测模型及计算结果
2.1徐变预测模型确定
徐变预测模型是各国研究者通过大量的试验,拟合出来的经验公式,考虑了各种影响混凝土收缩徐变效应的因素。CEB-FIP1990模型由系数相乘得到,分别为名义徐变系数及徐变发展系数,ACl209模型则采用了双曲线形式来表示徐变系数。各规范规定的混凝土徐变预测模型中的影响因素存在差异,但主要影响因素如湿度、加载龄期、构件尺寸这些影响徐变的主要因素都被写进公式中,对不同的混凝土收缩徐变预测模型提出了不同的混凝土徐变系数的计算方法,反映了混凝土徐变的发展规律。对混凝土收缩徐变效应的分析,在工程实践中往往根据实际工程所处的环境以及相应规范选择合适的收缩徐变预测模型。JTG 3362-2018模型是CEB-FIP系列模式的衍生模式,对于徐变的预测最为精确,在国内外应用最为广泛。本研究中的钢-混组合连续梁桥位于海洋环境中,温湿变化随季节变化比较大。由此,確定采用我国最新JTG 3362-2018规定的徐变预测模型进行徐变性能研究。
2.2 加载龄期及湿度对组合梁桥位移的影响
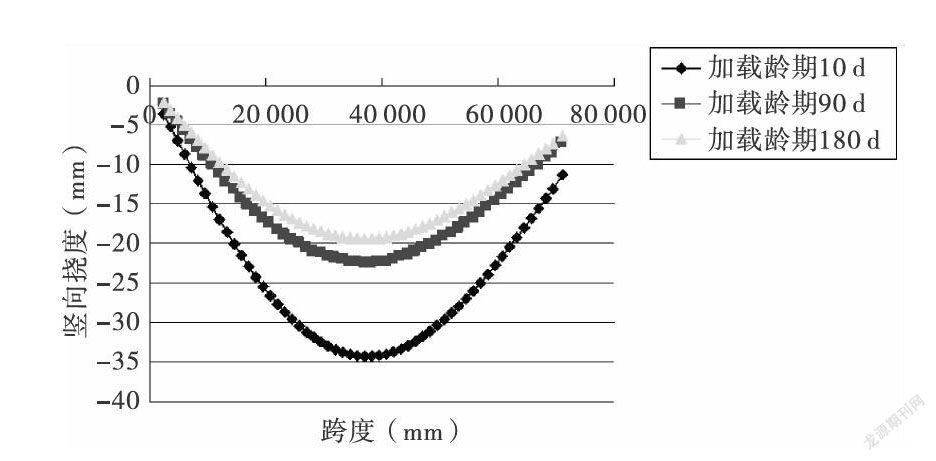
将钢-混组合连续梁所处位置的年平均相对湿度设置成70%,分别采用1000d和3000d两种不同成桥时间,计算对比不同加载龄期下钢-混组合连续梁徐变所产生的长期挠度值,获得徐变影响下钢-混组合连续梁桥边跨位置处竖向挠度值的大小,如图5所示。当成桥时间为1000d时,组合梁边跨的竖向挠度值会随加载龄期的增长,显著降低,当加载龄期的取值为10d,对应的边跨竖向挠度为34.8mm当加载龄期增长到180d,对应的边跨竖向挠度降低到19.5mm。当咸桥时间为3000d时,组合梁边跨的竖向挠度值会随加载龄期的增长,显著降低,当加载龄期的取值为10d,对应的边跨竖向挠度为37.2mm;当加载龄期增长到180d,对应的边跨竖向挠度降低到21.8mm。由图5可知,混凝土的收缩徐变作用对长期挠度的影响与加载龄期成反比,由于篇幅限制,仅给出成桥1000d时不同加载龄期下边跨竖向挠度曲线图。
加载龄期设置成180d,对应选取1000d和3000d两种不同咸桥时间,计算桥位区年平均相对湿度分别为50%、70%、90%时钢-混组合连续梁徐变产生的长期挠度,比较钢-混组合连续梁桥边跨竖向挠度值的大小,如图6所示。当成桥时间为1000d时,钢-混组合连续梁边跨竖向挠度将随着桥位处相对湿度变大而显著减小,桥位处相对湿度设置成50%时,边跨竖向挠度值达到-23.2mm;将桥位处相对湿度设置咸90%时,边跨竖向挠度降低到-14.6m。当成桥时间为3000d时,钢-混组合连续梁边跨竖向挠度将随着桥位处相对湿度变大而显著减小,桥位处相对湿度设置成50%时,边跨竖向挠度值达到-25.1mm;将桥位处相对湿度设置咸90%时,边跨竖向挠度降低到-16.3m。从图6可知,混凝土的收缩徐变作用对长期挠度的影响与桥位处湿度成反比,由于篇幅限制,仅给出成桥1000d时不同湿度下边跨竖向挠度曲线图。
2.3 成桥时间对组合梁桥应力的影响
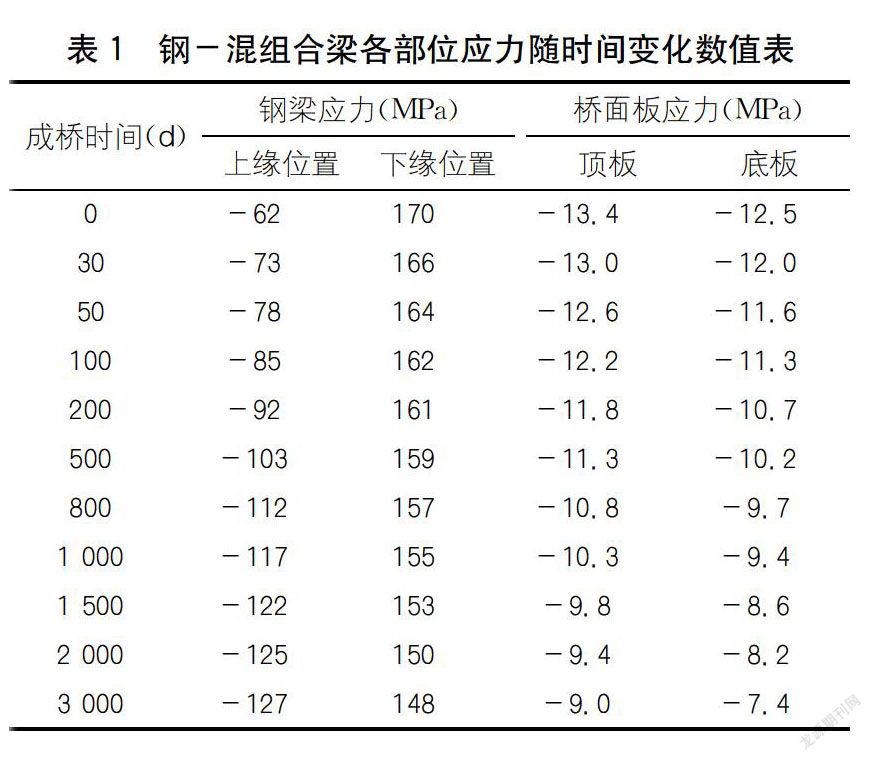
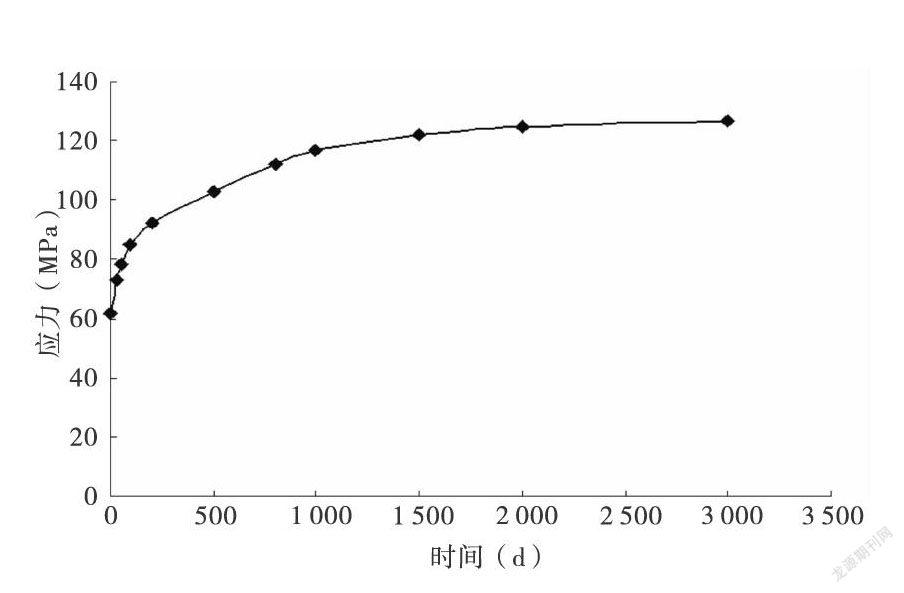
分别计算在不同的成桥时间下,组合梁桥边跨钢梁上翼缘最大压应力、下翼缘最大拉应力及预制桥面板的顶底板应力,并对比其应力随成桥时间变化情况,计算结果见表1和图7-9,表中受拉为正,受压为负。
由图7可见,随着成桥天数的增长,徐变效应作用下钢梁上缘压应力不断增加,并且在前三年时间压应力增长幅度较快,成桥1000d时,其边跨上缘压应力由62MPa增长到1171VIPa;2000d时,增长到125MPa;3000d时,上缘压应力增加达到127MPa。此时压应力增长已很缓慢,曲线的斜率区域平稳,基本趋于稳定。
图8表明,徐变对钢一混组合梁钢梁下缘拉应力的影响则相对较小。其初始成桥状态下钢梁下缘拉应力值为170MPa,成桥3000d时相应位置处的应力降低到148MPa,减小约13%。前三年时间减小较快,已减小接近70%。到成桥3000d时,钢梁下缘对应位置处的拉应力的降低幅度已经很小,基本趋于稳定。
同理计算得到混凝土板上下缘应力变化值(如图9所示),混凝土板上下缘压应力均随成桥时间增大而减小。
2.4 加载龄期对组合梁桥应力的影响
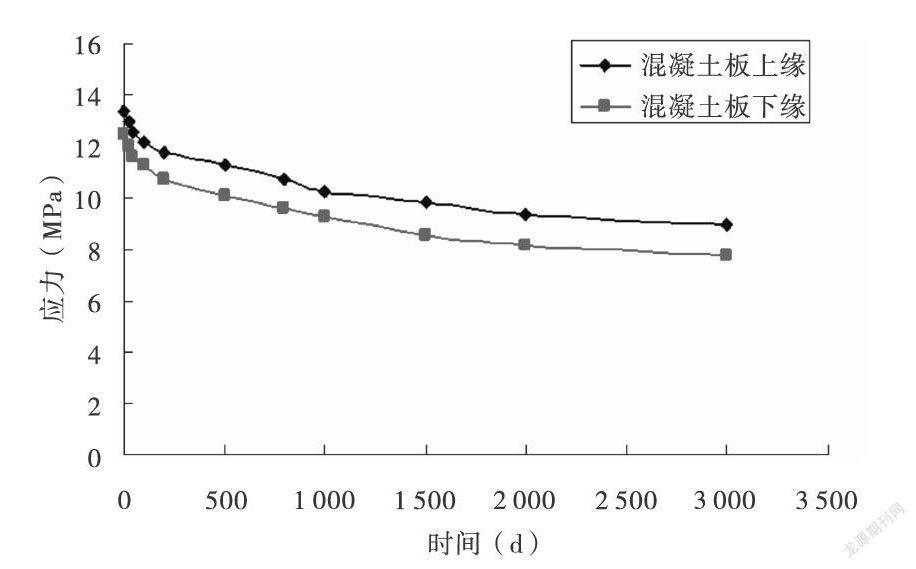
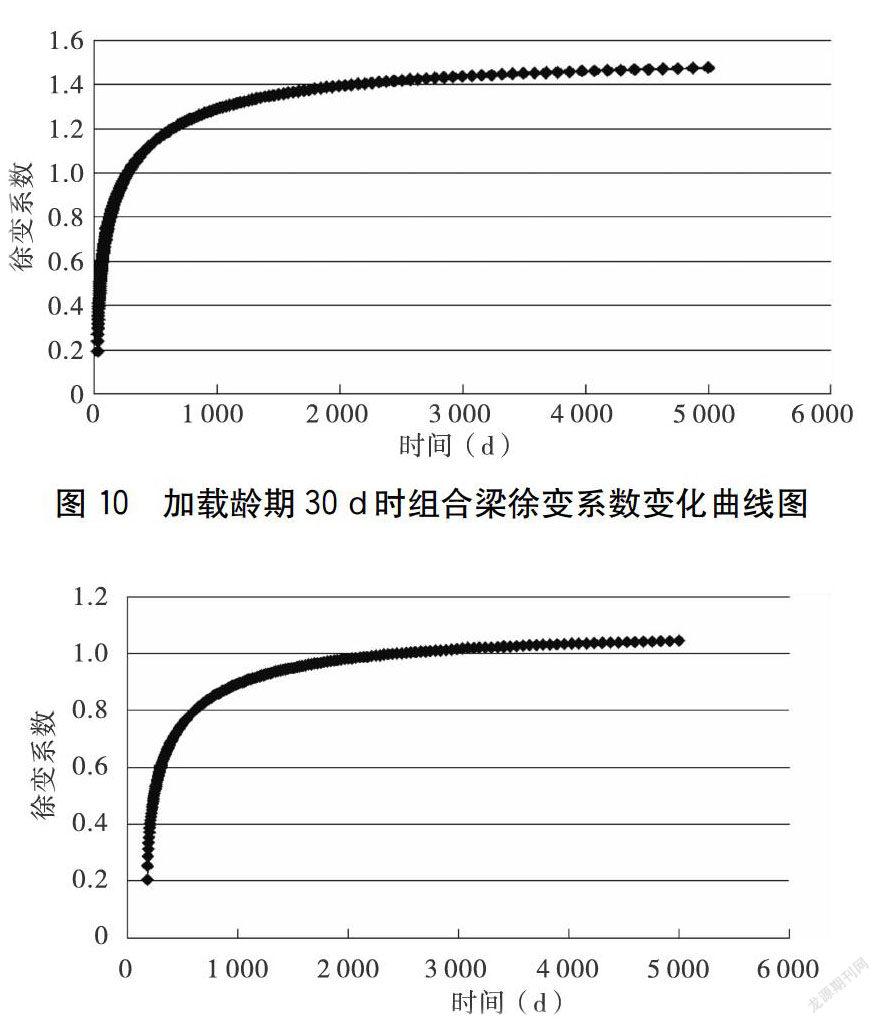
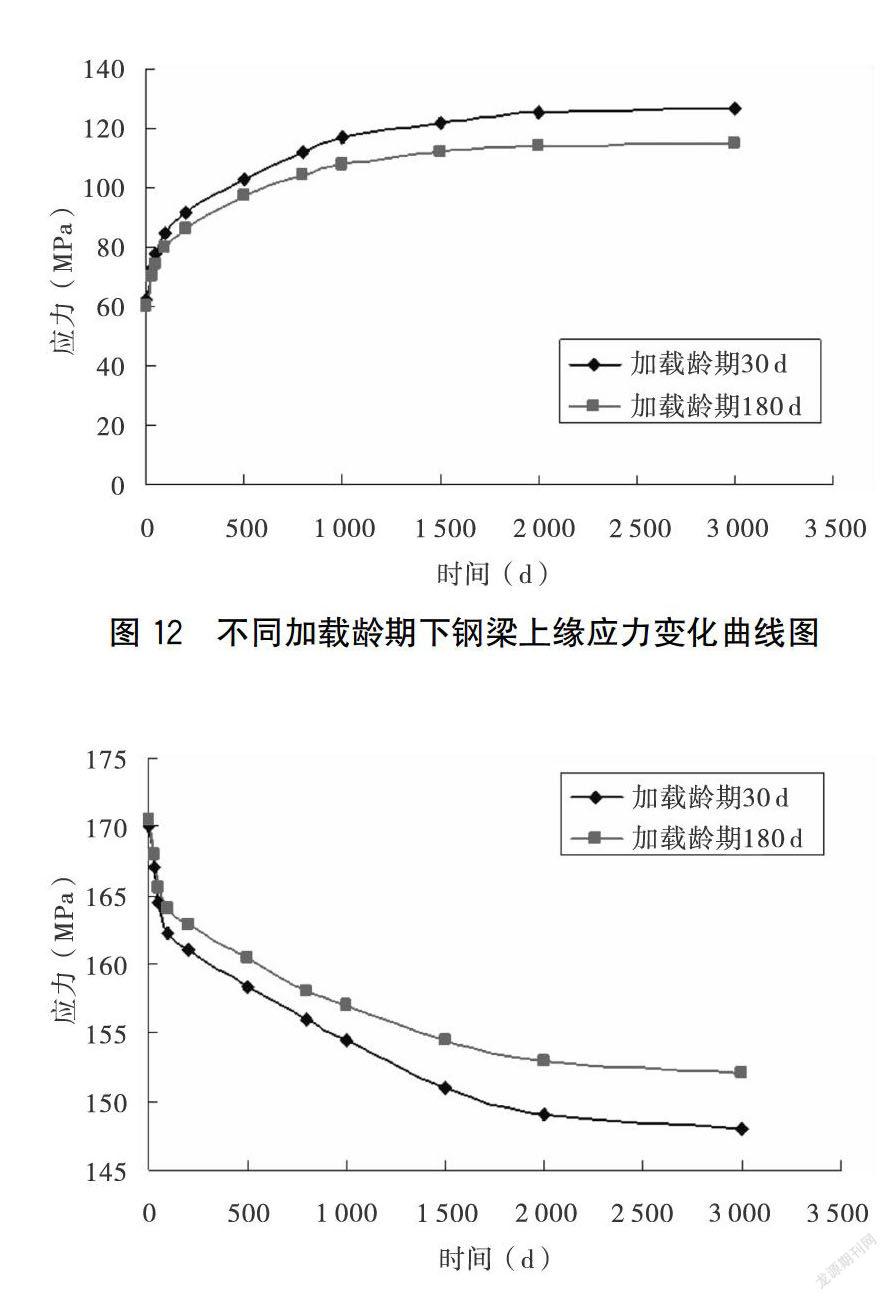
工程上将徐变引起的变形与结构瞬时弹性:变形之比定义为混凝土徐变系数。将桥位处年平均相对湿度定义成70%,计算不同加载龄期下混凝土徐变系数随成桥时间的变化关系,获得加载龄期分别设置成30d和180d时,钢-混组合连续梁桥边跨各关键部位的应力随时间变化值,如图10-13所示。
由图10和图11可知,混凝土的徐变系数与加载龄期成反比,在钢-混组合连续梁的施工架设过程中,将桥面板放置半年以上,可显著降低结构的徐变效应。
由下页图12可知,随着加载龄期的增长,徐变效应引起的组合梁应力变化越小。当混凝土加载龄期设置到30d,成桥时间1000d时,其边跨钢梁上缘压应力为117MPa成桥时间增长到2000d时,相应位置处的应力增大为125MPa;成桥时间增长到3000d时,相应位置处的应力增大为127MPa。当混凝土加载龄期设置到180d,成桥时间1000d时,其边跨钢梁上缘压应力为108MPa;成桥时间增长到2000d时,相应位置处的应力增大为110MPa;成桥时间增长到3000d时,相应位置处的应力增大为112MPa。
由下页图13可见,不同加载龄期对组合梁桥钢梁下缘拉应力也会产生影响。随着加载龄期增大,钢梁下缘应力随时间变化减小,加载龄期对钢梁上缘应力的影响较下缘应力影响更为显著。增大加载龄期可以显著降低由徐变作用所导致的应力变化。
2.5 湿度对组合梁桥关键部位应力的影响
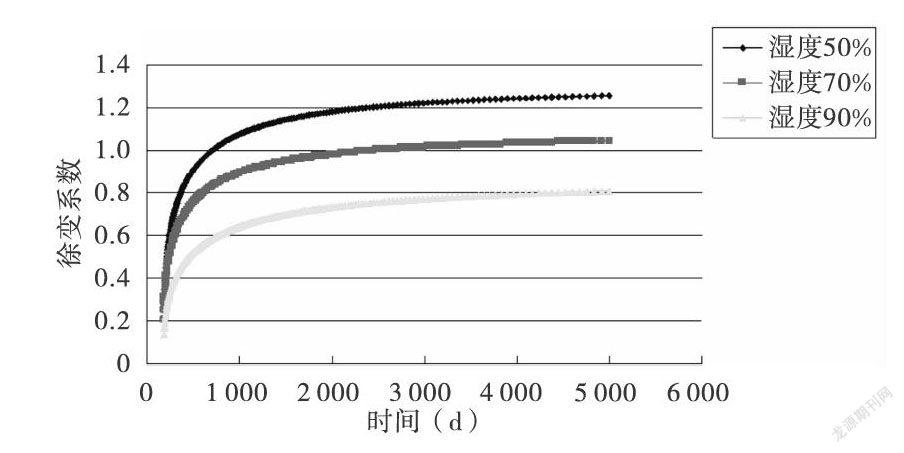
将加载龄期设置为180d,分析桥位处不同环境相对湿度下徐变系数随成桥时间变化的关系以及不同环境相对湿度对应的组合梁桥边跨钢梁各关键部位的应力随时间变化值,并对比其应力随时间变化情况(见图14-15)。由图14可知,随着桥位处环境相对湿度增大,徐变系数降低,两者成反比关系。
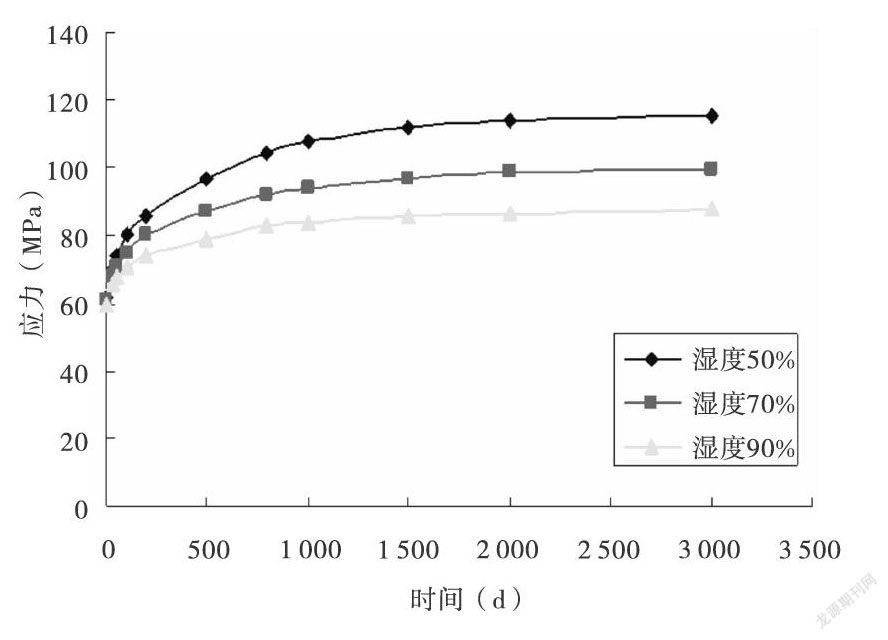
由图15可见,桥位处环境相对湿度越大,徐变引起的组合梁桥边跨钢梁各关键部位的应力越小。当将环境相对湿度设置成50%时,咸桥时间为1000d时,其边跨钢梁上缘压应力为104.5MPa;成桥时间增长到2000d时,相应位置处的应力增大为108.7MPa;成桥时间增长到3000d时,相应位置处的应力增大为110.8MPa。将环境相对湿度设置成70%,成桥时间为1000d时,其边跨钢梁上缘压应力为93.4MPa;咸桥时间增长到2000d时,相应位置处的应力增大为96.4MPa;成桥时间增长到3000d时,相应位置处的应力增大为98.1MPa。将环境相对湿度设置成90%,成桥时间为1000d时,其边跨钢梁上缘压应力为81.4MPa;成桥时间增长到2000d时,相应位置处的应力增大为83.2MPa;成桥时间增长到3000d时,相应位置处的应力增大为84.5MPa。
不同湿度对组合梁应力变化的影响也体现在钢梁下缘拉应力变化上,且环境相对湿度越高,钢梁下缘拉应力变化越小,但桥位处环境相对湿度对钢梁上缘应力的影响较下缘应力的影响更为显著。
3 结语
(1)本文建立了6×85m钢-混组合连续箱梁桥全桥精细化有限元模型,模型中考虑简支变连续以及顶升的施工工艺,以精确分析桥梁的力学行为,确定了适用于钢-混组合连续梁桥的徐变预测模型为JTG 3362-2018模型。
(2)本文详细分析徐变效应对钢-混组合连续梁桥长期挠度和应力变化的影响,得到了不同环境因素下,组合梁长期挠度值的大小,以及組合梁应力变化与环境因素之间的对应关系。徐变会引起钢-混组合连续梁桥截面应力和挠度的显著变化,设计和施工中不能忽略,应采取必要的措施降低徐变对组合梁的影响。

