浅谈社会稳定参数在经济增长中的应用
张继肖

[摘要]
在社会经济发展过程中,缩小贫富差距虽然有利于实现社会公平,但是如果过分追求社会公平,则可能会以降低社会效率、削弱创富机制的作用、将社会带入绝对贫困为代价。如何在社会经济发展中寻求公平与效率的平衡点,本文提出应采用考虑了人均财富占有量、人均GDP、收入基尼系数、财富基尼系数、洛伦兹曲线偏离度以及域外经济环境等因素在内的社会稳定参数作为参照坐标,来把握效率与公平之间的度。
[关键词]
社会总效用 公平 效率 社会稳定参数
维持社会经济的稳定发展,在收入分配方面需要保持一定的均衡。如果贫富差距过于悬殊,社会便有可能产生巨大动荡,但过分强调平均,又会导致社会效率降低,削弱创富机制的作用,将社会带入绝对贫困。如何在社会经济发展中寻求公平与效率的平衡点,即把握好兼顾公平和效率的“度”的问题,是政府部门应该认真思考的问题。
1 收入分配的不均衡影响着社会经济的发展
科斯定理指出:只要财产权是明确的,并且交易成本为零或者很小,那么无论在开始时将财产权赋予谁,市场均衡的最终结果都是有效率的,并可以实现资源配置的帕累托最优。在理论上,经济的外部性或者非效率可以通过当事人的谈判而得到纠正,以达到社会效益最大化[1]。
根据上面的表述,科斯定理可以理解为:在不经过谈判或交易的条件下,经济通常表现为外部性或非效率,在人为干预之前,谈判或交易成本的存在使得资源配置很难达到帕累托最优。将这一理论应用在收入分配领域,可表述为:在一个社会的分配模式中,让资源分配自动实现帕雷托最优,继而达到缩小贫富差距、避免社会动荡以及促进经济发展的目的是很难办到的事。
因此,当一个社会希望保持一定的经济效率,又希望社会成员之间的收入差距不至于过分拉大,就需要政府部门准确判定社会的稳定狀态,并从制度层面营造合理的市场条件,进行适当的政府干预,以接近社会收入分配方面的帕累托有效配置,避免马太效应产生的负面效应,进而实现社会发展目标。
2 用基尼系数判断社会稳定的局限性
作为反映统计差异性的指标,基尼系数通常被用来衡量居民之间的贫富差距。通过基尼系数的横向比较,可以知道各个国家或地区的贫富差异程度;通过基尼系数的纵向观察,可以对某一地区贫富差异程度在不同时期的变化情况进行分析。
虽然作为国际通用的指标,基尼系数具有综合性和概括性的优点,但它在运用于社会实践时也存在着一定的局限性。理论界对基尼系数局限性讨论的主要焦点之一在于洛伦兹曲线与基尼系数对应的非唯一性,即不同的洛伦兹曲线可能对应着相同的基尼系数[2]。
在图1中,人们所考察的两个社会模型中有着两条不同的洛伦兹曲线,但它们所对应的基尼系数却是相同的。倘若利用这个基尼系数来比较这两个社会模型中分配结构的差异程度,就会得到两个社会模型中的居民具有相同收入差异程度的结论。而这显然是不正确的。实际上,通过分析可以发现,由于线1的拐点(曲线斜率为1的位置)低于洛伦兹曲线的中心点,而线2的拐点高于洛伦兹曲线的中心点(下文中,对洛伦兹曲线拐点偏离中心点的程度,称为洛伦兹曲线偏离度),因此线1所描述的分配状态更应引起政府部门的注意,因为此时该社会模型中低收入群体的相对贫困程度要高于线2所对应的社会模型中低收入群体的相对贫困程度。如果以这样的基尼系数作为对社会收入分配进行管理的参数时,其推出的政策将会与社会的实际要求出现背离。
其实,如果再深入探究一下,就会发现在以基尼系数作为对社会分配进行管理的参数时,不仅必须考虑到该社会在同一基尼系数下社会财富分配的具体状态,而且还要考虑到该社会整体(主要是人均)财富量、人均收入(本文使用人均GDP)增长或衰退情况、洛伦兹曲线偏离度以及域外经济环境等影响因素。抛开上述条件而直接用一个简单的基尼系数作为警戒线来判断社会的稳定状况,进而寻求公平与效率的平衡点,效果必然要大打折扣。
上述分析并不是说利用基尼系数的警戒线来判断社会稳定状况、进而寻求公平与效率平衡点是错误的,而是说在考虑了社会人均财富量、人均GDP等影响因素之后,在考量社会财富分配状况的优劣时不宜只用基尼系数这一相对简单的指标,而应该用一个考虑了人均财富占有量、人均GDP、收入基尼系数、财富基尼系数、洛伦兹曲线偏离度以及域外经济环境等因素在内的“社会稳定参数”来进行描述。
3 关于社会稳定参数的描述
第一,假设在社会财富总量为Q1、GDP总量为Q2、人口总量为M、人均财富占有量为q1(q1=Q1/M)、人均GDP为q2(q2=Q2/M)、综合基尼系数为K时(综合基尼系数K=(A4Ki+A5Kw)/2;其中:Ki为收入基尼系数;Kw为财富基尼系数),洛伦兹曲线偏离度为Ld,在考虑了域外经济环境的影响后,社会的稳定状态为F。那么这个与q1、q2和K等因素相对应的F则被用来表示衡量该社会稳定状态的参数,将其命名为社会稳定参数F。
(1)由于人均财富占有量q1、人均GDPq2与社会的稳定正相关,因此应将其两者的加权平均数置于分子位置。
(2)由于综合基尼系数K与社会的稳定负相关,因此应将其置于分母位置。
(3)洛伦兹曲线偏离度Ld的位置:
如果其拐点L(曲线斜率为1的位置)居于正中(此时L取值为0.5)则Ld=L/0.5=1;如果居于正中偏上(如线2),此时L取值>0.5,则Ld=L/0.5>1;如果居于正中偏下(如线1),此时L取值<0.5),则Ld=L/0.5<1。据此,Ld与社会的稳定正相关,将其置于分子位置。
于是得到该社会稳定参数F为:
F={﹝A1(Q1/M)+A2(Q2/M)﹞×A3Ld}/﹝(A4Ki+A5Kw)/2﹞
或F=(A1q1+A2q2)×A3Ld/K
式中:A1——人均财富对社会稳定参数的影响系数
A2——人均GDP对社会稳定参数的影响系数
A3——洛伦兹曲线偏离度对社会稳定参数的影响系数
A4——收入基尼系数对综合基尼系数的影响系数
A5——财富基尼系数对综合基尼系数的影响系数
对于A1至A5数值的确定,应该在大量接近事实数据的支撑下,通过回归分析导出。
显然,F值越大,该社会的稳定性越强。
第二,在不同年份,社会稳定参数F会有相应的对应值。通过对观察年社会稳定参数FN与基准年社会稳定参数F0的比较,就能够看到社会在处于财富总量、GDP总量及人口总量变动的条件下,社会稳定状态是改善、不变还是恶化了,即:FN>F0、FN=F0或FN
需要注意的是,在分析过程中,代表年限的N值的取值不宜过大。
第三,考虑到外界因素的影响,即域外社会经济及社会财富处于增长(或衰退)过程中,在一个开放的社会环境中,这一因素必然要影响到该社会的稳定状态。也就是说如果被观察的社会经济及财富增长(或衰退)均与外界一致,在不考虑其他因素(如人口数量、基尼系数及洛伦兹曲线偏离度等)的条件下,其稳定参数没有变化。因此在进行统计计算时,该社会的经济及财富增长(或衰退)应该剔除外界经济及财富的增长(或衰退)。被剔除了外界经济及财富增长(或衰退)的数据我们称之为有效经济及财富增长(或衰退)。
社会稳定参数F仅适用于某一个国家或地区在不同时间上稳定状况的比较,它只有在用该社会的一组在不同阶段的统计数值进行比较才有意义,孤立的只看其中任何一个绝对数值则没有任何意义。
社会稳定参数与基尼系数K根本的不同在于:它在对社会稳定状况进行观察时,将不考虑社会经济发展状况的、静态的、不考虑洛伦兹曲线形状以及域外的经济环境的绝对数值,替换为考虑到社会经济发展状况的、动态的、考虑到洛伦兹曲线形状以及域外经济环境的相对数据。
4 社会稳定参数变化举例说明
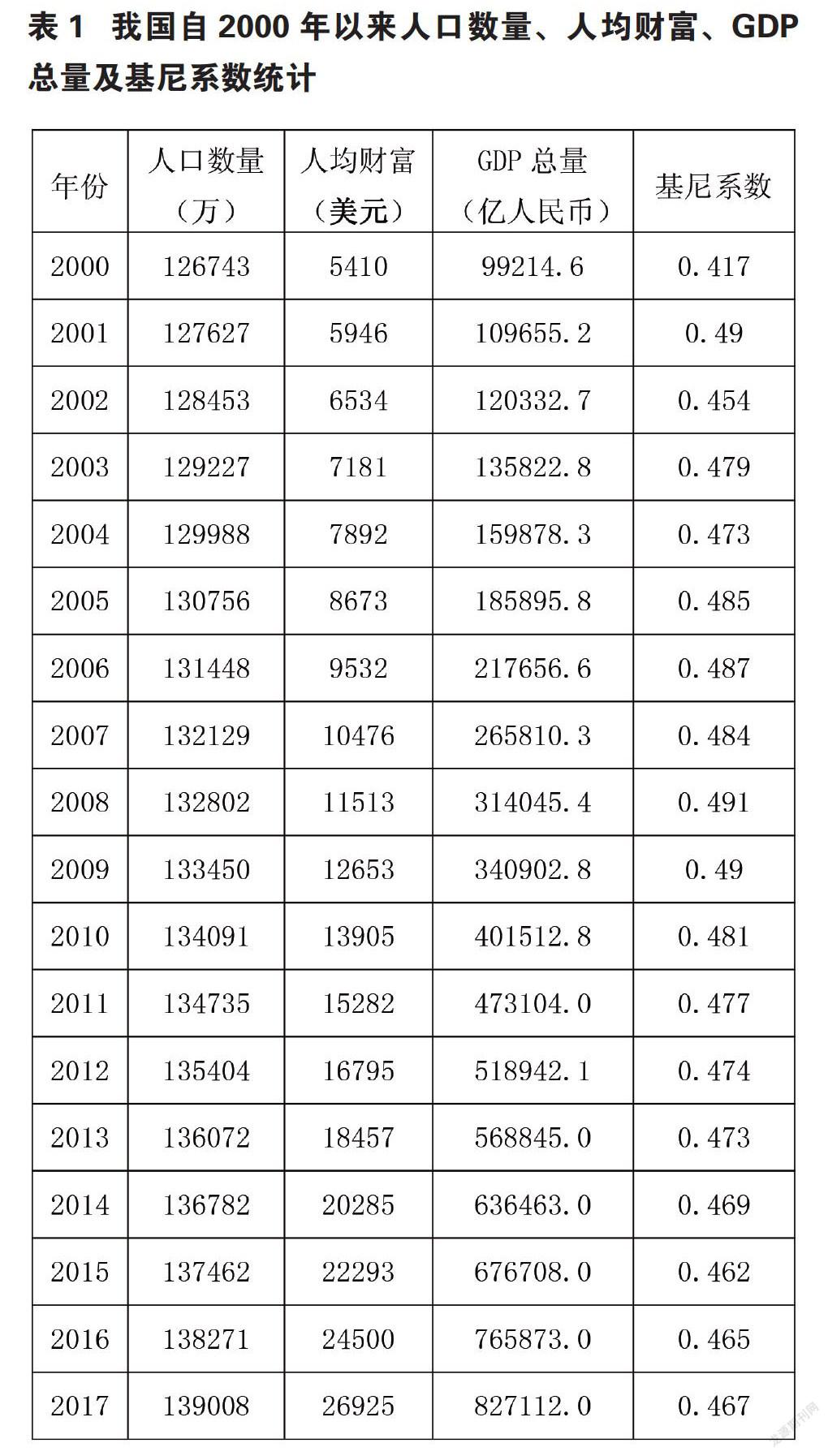
下面根据网络上所能查到的部分数据,考察一下我国从2000年到2017年社会稳定参数的变化情况。
人口数量、GDP总量及基尼系数均采用国家官网公布的数据。由于缺乏我国财富总值的官方资料,本文以瑞信研究院提交的2017年《全球财富报告》数据为依据。该报告显示,从2000年到2017年的18年间,我国成人平均财富从5410美元增加至26870美元[3]。为方便计算,将我国成人平均财富的增加过程看作匀速增长过程,即每年增长约9.9%。
(1)在表1中所列的GDP没有考虑到通货膨胀的因素。由于没有各年通货膨胀的详细数据,以下以2000年為基数,按照国家官网公布的各年经济增长率来进行修正。
(2)考虑到美元贬值问题,依据巴菲特观点,从1965年到2011年47年间美元购买力贬值为86%,据此近似估计美元年均贬值率为4.3%,即我国成人平均财富增速按9.9%-4.3%=5.6%计算并按照1比6.5的汇率换算成人民币。
(3)根据前面的理论,统计分析要考虑到域外社会经济及社会财富处于增长或衰退状况。由于缺乏准确资料,为简化起见,下面按3%的增速计算域外社会(全世界)经济及社会财富增长情况,在剔除3%的增速后,我国成人平均财富有效增速按2.6%计算,我国平均GDP有效增速按各年GDP增速减去3%来计算。
(4)由于缺乏对于A1、A2的验证数据,课题组对A1、A2之和的取值以1为基础数,以2000年中国经济发展水平为分析起始时间,以2017年中国经济发展水平为分析结束时间,A1、A2的取值由A1
(5)由于缺乏财富基尼系数的数据资料,课题组采用国家官网公布的基尼系数作为综合基尼系数。
(6)由于缺乏洛伦兹曲线偏离度的数据资料,为计算简便,A3Ld取值为1。
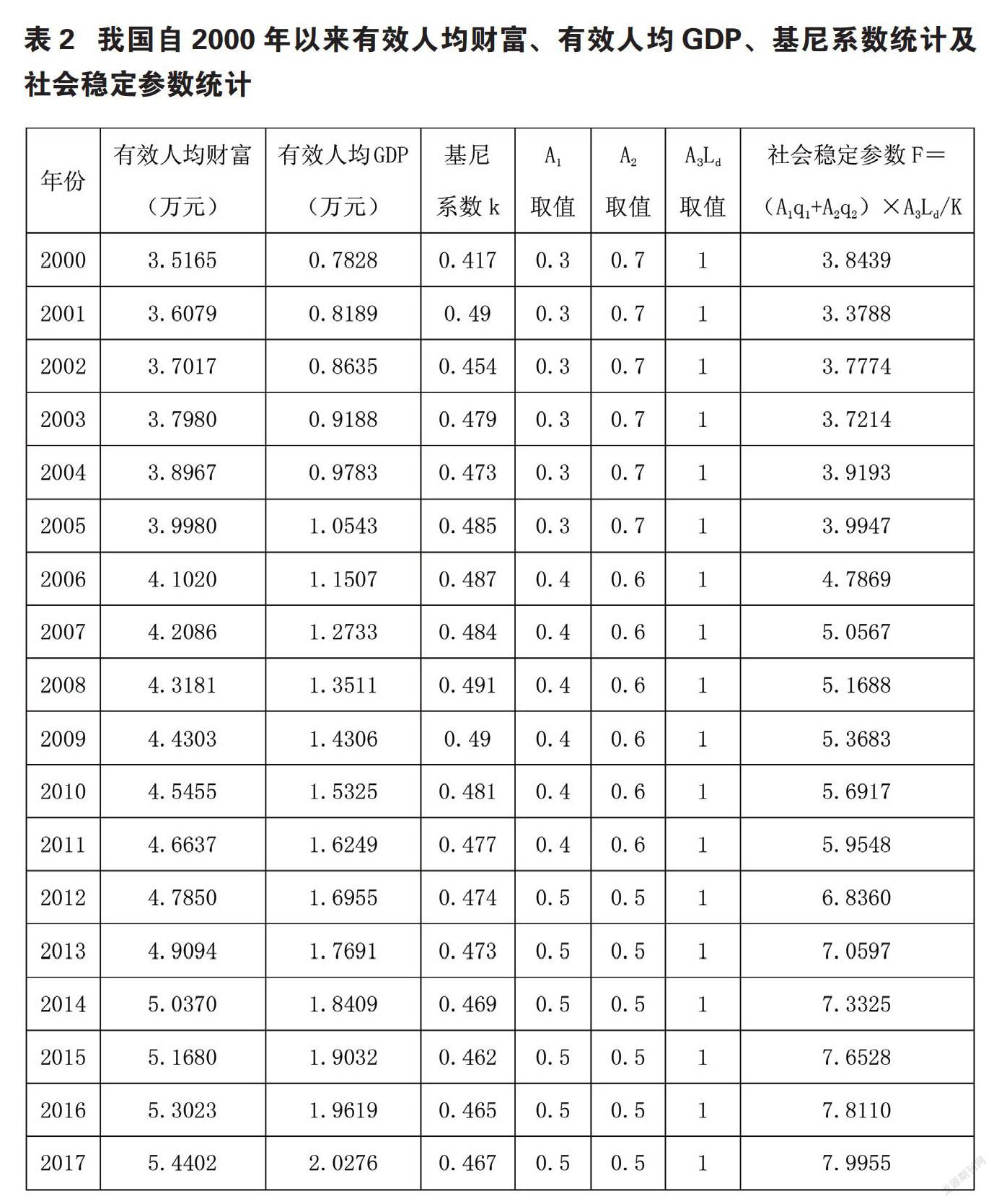
(7)表2中人均财富、人均GDP均以万元为单位。
根据以上分析结果,将我国从2000年到2017年人均财富、人均GDP、基尼系数及社会稳定参数的变化情况作图2如下:
从上面的分析可以看到,虽然我国的基尼系数一直超过国际公认的警戒线0.4,并且一直居高不下,但社会稳定状况却没有出现明显的问题,并且逐年向好。这主要得益于我国持续高速且较为稳定的GDP增长和社会财富增长速度,超过了域外社会(全世界)经济及社会财富的增长速度。
5 让社会稳定参数为发展中国家经济发展服务
在不同的社会条件下,对于收入分配是否合理的判断标准会有所不同,因此在其寻求经济效率与确保社会相对公平时,对于最佳平衡区间的选择也会有所不同。对于条件优越的发达国家或地区来说,在寻求经济效率与确保社会相对公平的最佳平衡区间时,可以将公平作为优先选项;而对于基础条件较差且积极寻求经济快速发展的发展中国家或地区来说,在寻求经济效率与确保社会相对公平的最佳平衡区间时,往往可以在确保社会稳定的前提下,将完善社会创富机制、寻求高效发展作为优先选项。
在理论上,一个社会在寻求经济效率与确保社会公平的最佳平衡区间时,应满足的条件是:由该社会因实现公平而产生的边际成本等于由此造成社会效率相应降低而增加的边际成本。但在现实中,发达国家可接受因实现公平所产生的边际成本稍高于由此造成效率相应降低而增加的边际成本;而发展中国家或地区掌握的尺度应该与此相反,但前提是因不公平而产生的边际成本不能高于警戒线。这里所说的警戒线不是作为国际通用指标的基尼系数,而是本文描述的社会稳定参数,即当一个发展中国家或地区在寻求经济效率与确保社会相对公平的最佳平衡区间时,应该确保该社会稳定参数逐渐加大或保持不变。
对于社会公平的矛盾较为突出的发展中国家或地区,其政府部门在力图缩减社会分配差距时,应该利用好市场这只“看不见的手”,从社会运行机制入手,使社会公平的实现趋于内生和高效。
(1)发展中国家或地区要视自身发展状况,在营造合理的市场环境上下功夫,利用竞争市场的力量分配要素禀赋。按照福利经济学第一定理的观点,只要在经济主体的偏好被良好定义的条件下,再分配的价格均衡都应该是帕累托最优的[4]。市场在资源配置中起决定性作用,是实现收入分配方面的帕累托效率最有效的方法。政府部门要加大市场调节力度,从制度上保证市场在资源配置中起决定性作用,以确保提高社会效率和实现公平的效果。
(2)由于每个社会成员初始的要素禀赋存在一定差异,因而导致收入方面也存在较大差异,这一点在尚处于较为贫困的发展中国家或地区更为突出。发展中国家或地区的政府部门应该在缩小社会成员初始的要素禀赋差异上投入更多的资源,因为这样的投入比起直接依靠二次及三次分配手段调整社会成员的收入状态来说,更带有根本性的“杠杆”效果。福利经济学第二定理告诉我们,只要条件具备,各种具有帕累托效率的资源配置都会趋于竞争均衡[5]。营造合理的市场氛围,改善每个社会成员之间要素禀赋的初始分配状态,将有助于缩小社会成员初始要素禀赋存在的差异,使社会中各种具有帕累托效率的资源配置趋于竞争均衡。
(3)在利用第二次尤其是第三次分配手段对收入分配方面存在的社会问题进行调整时,要更多的利用“杠杆”性的手段而非直接的行政干预。
在利用税收来调节收入方面的差距时,应该根据社会经济发展情况,不断地对税收结构进行优化。在加大高收入人群的个人所得税在税收总额中所占比重的过程中,应该以因社会公平的实现而产生的边际成本等于由此造成社会效率相应降低而增加的边际成本为均衡点。
在社会经济发展状况较好的条件下,因实现公平所产生的边际成本可以稍高于由此造成社会效率相应降低而增加的边际成本;而在社会经济发展状况恶化的条件下,因实现公平所产生的边际成本應该稍低于由此造成社会效率相应降低而增加的边际成本,但前提是其因不公平而产生的边际成本不能高于警戒线。即在寻求经济效率与确保社会相对公平的最佳平衡区间时,应该使该社会稳定参数逐渐加大或保持不变,以此实现对收入分配的合理调控。
(4)实现第三次分配的手段可以多样化,即通过加大转移支付来减轻低收入群体负担。政府部门应该要求或引导富人群体通过消费、创造就业和其他机会,在事实上形成转移支付,这样不仅可以有效地改善收入分配状况,还会对提高社会经济效率产生良性效应,即利用所谓的“涓滴效应”来解决问题。
此外,政府部门应该在第三次分配的整体布局上做好顶层设计,使该项工作更有效率也更趋经济。
总之,对于发展中国家或地区来说,通过解决好公平与效率的平衡问题以保证社会维持高效、平稳、健康的运行是至关重要的。只有找准社会经济发展中公平与效率的平衡点,使社会稳定参数保持在相对合理的范围之内,营造好合理的市场条件,才可以接近收入分配方面的帕累托有效配置,真正有效解决社会经济发展过程中公平与效率之间的矛盾。
利用社会稳定参数作为衡量社会稳定状况的参照坐标是本文提出的新理念,其效果还有待于进一步的理论分析与实践验证。
(作者为天津工业大学继续教育学院副教授,中国市场学会理事)
(本文为天津市哲学社会科学研究规划资助项目(TJYJ18—012)阶段性成果论文;曾由天津市社会科学界联合会智库工作处提交2018天津夏季达沃斯论坛交流)
参考文献
[1]张永良.经济学基础(第二版) 北京理工大学出版社 2018.2 P166.
[2]苍玉权.论基尼系数的局限及调整 数量经济技术经济研究 2004.4.
[3]瑞信研究院(Credit Suisse Research Institute) 全球财富报告 2017.
[4]田国强.高级微观经济学 中国人民大学出版社 2016.11 P 547/554.
[5]彭春燕.微观经济学 北京理工大学出版社 2016.1 P184.

