基于虚拟结构优化模型的多机器人编队形成方法

芮可人 王丽华 谢能刚

摘  要：虚拟结构法可以使多机器人保持高精度的队形编队，本文提出一种基于进化算法的虚拟结构优化模型，以虚拟队形中心坐标和第一个预定节点的方向角为设计变量，通过进化迭代得到最优的期望队形和各机器人与固定节点的分配方法。仿真结果表明，该方法能够让多机器人形成期望的正n边形编队和直线型编队。

关键词：多机器人编队;虚拟结构;进化算法

中图分类号：TP242.6     文献标识码：A 文章编号：2096-4706（2019）18-0056-03

Abstract：The virtual structure approach can guarantee the high-precision formation of multi-robots. This paper proposes a virtual structure optimization model based on evolutionary algorithm. The center coordinates of the virtual formation and the orientation angle of the first predetermined node are used as the design variables. The evolutionary iteration yields the optimal expected formation and the allocation method between robot and fixed node. The simulations demonstrate that this approach is capable of achieving regular n polygon formation and linear formation for multi-robot.

Keywords：multi-robot formation;virtual structure;evolutionary algorithm

0  引  言

機器人编队是多机器人协作的基础，编队体现了机器人通过传感器感知外部环境，并依靠这些信息完成机器人之间、机器人与外部环境之间的互动能力。这些互动使得机器人之间保持固定的方位和距离，从而让整个机器人编队形成一个整体。目前采用较多的编队算法有：领航跟随法[1]、虚拟结构法、人工势场法和基于行为法等。其中虚拟结构法可以满足精度较高的队形控制要求，其基本思想是将一队机器人看作刚体结构中的质点，在刚体运动过程中，质点的相对位置保持固定，即多机器人编队在运动过程中保持固定队形。此前，M.Anthony和Kar-Han Tan提出虚拟结构的概念，结合机器人运动学给出机器人保持结构队形行进的控制律。Magnus Egerstedt和Xiaoming Hu结合虚拟领航法和虚拟结构法，通过机器人分别跟踪自身的参考点，将机器人协调问题解耦为一个路径规划问题和一个跟踪问题。Norman和Hugh采用虚拟结构法和同步技术相结合研究飞行器的队形控制问题，增强了队形控制能力和效率。Wei Ren提出一种分布式虚拟结构的多飞行器编队算法，相邻飞行器之间通过通信得到同步协调向量并据此得到在虚拟结构中的对应位置。在目前的文献资料中，一般在多机器人分布的区域内随机指定一个点或者以初始分布的形心作为期望队形的中心点，并以此中心点生成虚拟结构。本文采取进化算法优化虚拟结构，得到期望队形中心点的最优位置和各机器人与固定节点的分配方法。

1  多机器人形成期望编队的计算模型

1.1  共同知识

（1）任一机器人都知道其他机器人的位置（通过感知和通讯手段获得）。

（2）所有机器人都知道期望的编队队形。

（3）所有机器人都知道编队规则。

1.2  基于虚拟结构优化模型的编队规则

1.2.1  优化模型

假设参与编队的机器人数量为n，n个机器人的初始位置分别为（x0i，y0i）（i=1，2，…，n）。期望队形取两种：边长为d的正n边形和间距为d的直线队形。

2  仿真实验

为了验证本文算法的有效性，设计了以下仿真实验：机器人随机分布在仿真环境为30×30的矩形区域内，任务要求多移动机器人在工作环境中通过进化算法得到期望队形位置和最佳分配策略。进化算法的参数：种群数量L=1000，最大进化代数kmax=120，收敛判定小数ε=0.0001，正n边形的边长d=6。

2.1  期望队形为正n边形

机器人数量为5时，图3为优化的迭代过程，可以看到，随着进化代数的增加，目标函数值形成的柱体高度减小，位置下降，这表示队形中心位置坐标（xc，yc）和第一个预定点的方向角φ逐渐趋于最优值。根据进化算法得到的最优值，依次生成最优队形的节点以及各节点与各机器人之间的对应关系，如图4所示，实心三角形符号▲表示进化过程终止时最优的队形中心位置。○表示机器人的初始位置，*表示机器人期望队形固定节点的位置，相同颜色的○和*表示每个机器人所对应的队形点。

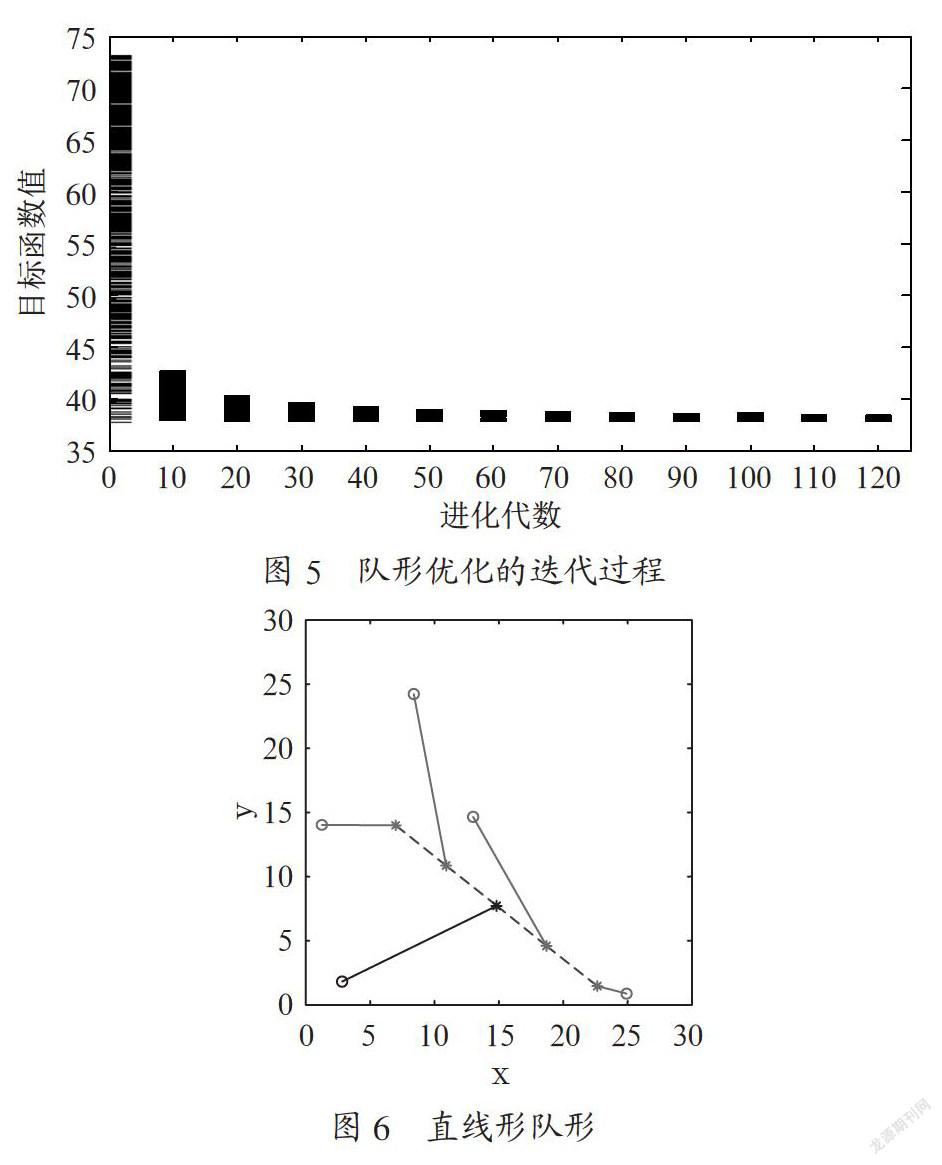
2.2  期望队形为直线队形

以n=5的直线队伍为例，队形中相邻机器人的间距d=5，图5表示优化的迭代过程，图6为最终的直线队形及各节点与各机器人之间的对应关系。

3  结  论

本文针对多机器人编队任务，提出采用进化算法得到最优虚拟队形中心位置和第一个队形点的方位角，根据队形的形成规则得到队形固定节点。仿真结果表明，算法可以得到最后的收敛解。同时本文提出一种机器人到达固定节点的分配方法，使得每个机器人到达其预定节点所移动的距离尽可能相等且保证整个机器人系统运动的距离较短。

参考文献：

[1] 董胜龙，陈卫东，席裕庚.多移动机器人编队的分布式控制系统 [J].机器人，2000，22（6）：433-438.

[2] 谢能刚，孙林松，方浩.基于进化策略的拱坝体型优化设计 [J].水利水运工程学报，2006.3（1）：24-29.

作者简介：芮可人（1993.08-），男，汉族，安徽安庆人，硕士研究生，研究方向：移动机器人算法。