设置公交专用道的交叉口群交通组织及绿波协调
唐博 王颖

摘 要:交叉口通行的特点是交叉口之间距离短并且有很强的关联性,尤其是在设置了公交专用道后,通行条件和信号配时均需要保证公交优先。本文选取银川市贺兰山西路的四个连续的交叉口作为研究对象,通过对数据分析处理,利用数解法完成了上述连续四个交叉口的绿波协调配时,在保证公交优先的前提下,实现车辆连续的通过距离较近的交叉口,使车辆延误降低,道路排队长度减少,通行能力得到提高。
关键词:公交专用道;交叉口群;信号控制;绿波协调
中图分类号:U491.12 文献标识码:A 文章编号:2096-4706(2019)18-0011-03
Abstract:The characteristics of intersection traffic are short distance and strong correlation. Especially when bus lanes are set up,both traffic conditions and signal timing need to ensure bus priority. In this paper,four consecutive intersections of Helanshan West Road in Yinchuan city are selected as the research objects. Through data analysis and processing,the green wave coordinated timing of the four consecutive intersections is accomplished by using numerical method. On the premise of ensuring bus priority,vehicles can continuously pass through the nearer intersections,thus vehicle delays and the length of road queuing can be reduced,and the traffic efficiency will improve.
Keywords:bus lane;intersection group;signal control;green wave coordination
0 引 言
城市交通量的急剧上升使得城市道路体现出交通流量大、密度大、车辆溢出等特征。当交叉口的交通量达到饱和时,车辆在连续的交叉口周期中会出现拥堵排队的现象,尤其是在实施“公交优先”策略的情况下,普遍在用的公交专用道以及与其匹配的交叉口公交优先配时,使得交叉口群交通组织更加复杂,一旦设置不合理必然会使道路通行能力下降,甚至会造成交通事故和交通拥堵的发生;对于驾驶者而言驾驶体验感下降,车辆油耗也会随之增加。
本文以银川市贺兰山西路上设置有公交专用道的连续四个交叉口构成的交叉口群做为研究对象,依据交通特征参数调查和分析结果,对于四个交叉口双向的信号配时进行绿波协调控制方案设计,希望能够在保证公交优先的前提下,提升整个交叉口群的通行效率和出行体验。
1 交叉口群信号控制现状计算分析
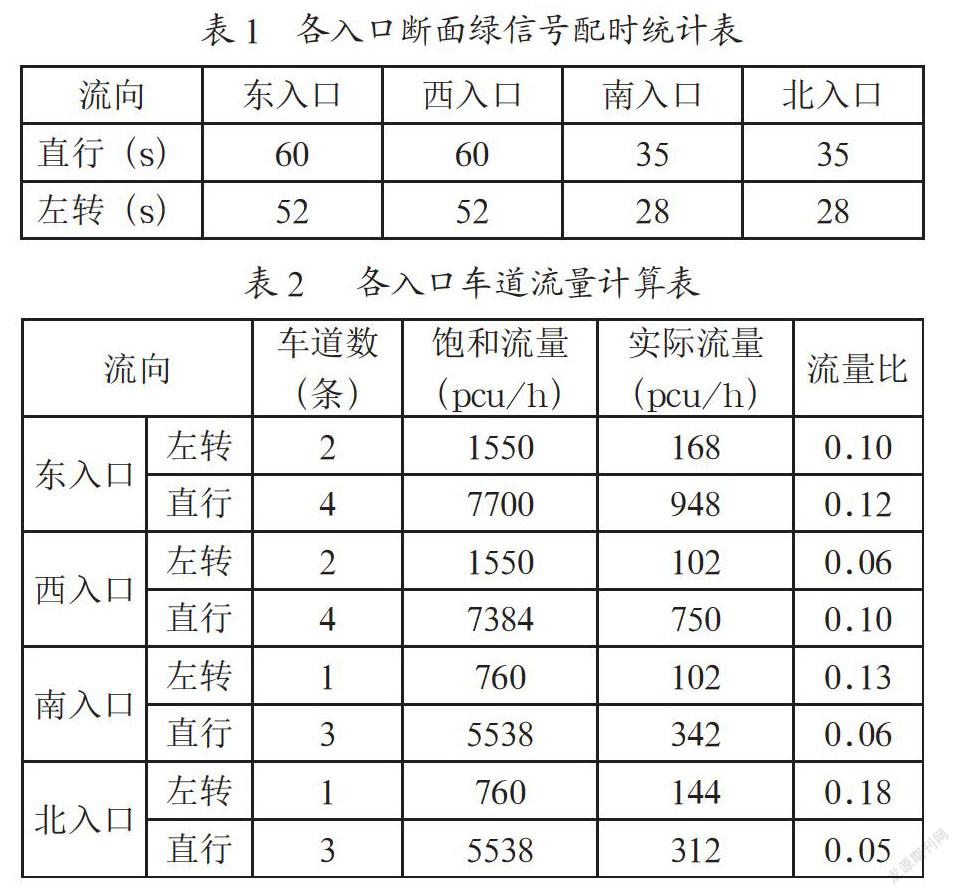
本文将上述交叉口群的四个交叉口由东向西编号为A、B、C、D。本文以A路口为例进行交叉口基础数据的分析。表1为对象交叉口各入口断面绿信号配时情况,表2为与表1对应的各车道交通流统计和计算结果。
之后利用韦氏最佳信号周期时长计算交叉口A的最佳配时,如表3所示。
依照上述方法,可以分别对剩余三个交叉口B、C、D进行最佳配时计算,在单个交叉口条件下,对于信号配时进行独立优化。
2 绿波协调信号控制方案设计
绿波协调信号控制常采用的两种方法是最大绿波带法和最小延误法。其中以最大绿波带为目标的主要有图解法和数解法,本设计将对贺兰山西路四个连续交叉口构成的交叉口群,在保证公交优先的前提下,应用数解法进行信号协调控制。
2.1 理想位置的确定
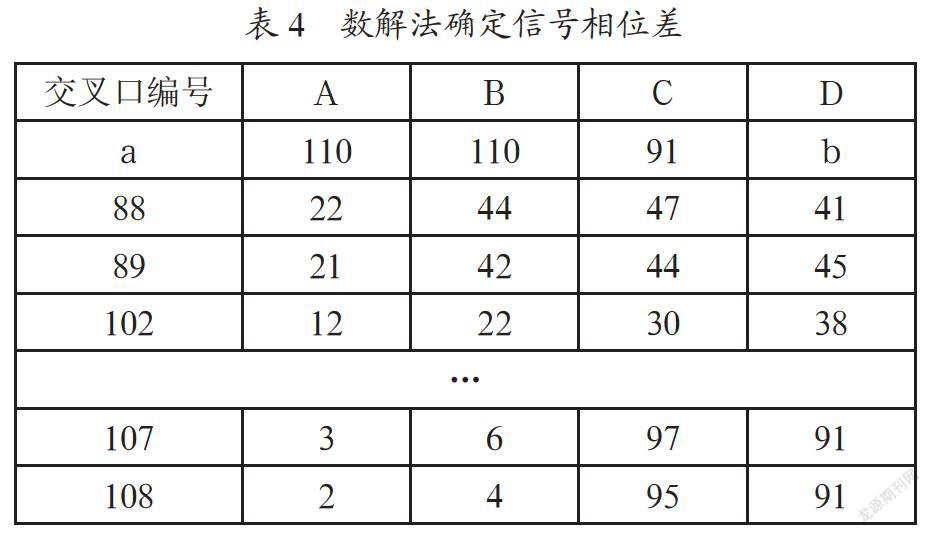
数解法是干道信号协调的重要方法之一,通过数解法确定信号相位,调整系统中实际位置距离理想位置的最大挪移量来确定最后的协调方案。A、B交叉口之间距离为1100m,B、C为1100m,C、D为916m,以10m为单位取有效数字110,10,110。算得关键交叉口B周期时长为Y=115-6=109s,相应的带速为70km/h,约为19m/s。首先计算VY/2=19*109/2=103.5(取有效数字103)。从A开始作為起始信号,则其下一个交叉口同A相距VY/2m,VYm,3VY/2m……处即为正好能组成交互式协调或同步式协调的“理想信号”位置。以103-15或103+15作为最合适的VC/2变动范围的值,即取88~118m的范围,将此范围填入表4的a列内,a这一列所表示的就是假想理想位置。
以a=88行为例,A、B交叉口的实际间距为110m,与理想信号位置间距88的差值为22,将22填入AB间的一列内。表示B与理想位置的距离为22,当B向前挪离220m就可与A恰好组成交互式协调。B、C交叉口的实际距离为110m,B与理想信号位置b相差22,D、C交叉口的实际距离是91m,C与理想信号位置相差44,即C与理想位置相差为44,将44填入B、C间的一列内。依次类推,计算至C、D间的列。a=88这一行的计算结束。
以a=88一行为例,将假定的理想位置与实际位置的间距按从小到大上的位置排列,然后做它们间隔之间的差值,将此差值最大者记为b。a=88一行b的值为41。依此类推,计算a=88~108各行b的值。
2.2 确定最优信号位置和相位差
由表4中可知,当a=102时,b=38时,车俩从交叉口A到D行驶时各交叉口距离理想信号位置的相对移动量最小,即当VC/2=1020m时可以达到最好的协调效率。A-C同理想信号位置之间的移动量之差最大,则A与理想位置的移动量为(a-b)/2=64m,即各实际信号位置距理想信号位置的最大挪移量为64m。理想信号位置距A为80m,即自前移80m即为第一理想信号位置,然后依次每1020m间距将各理想信号位置列在各实际信号位置之间。
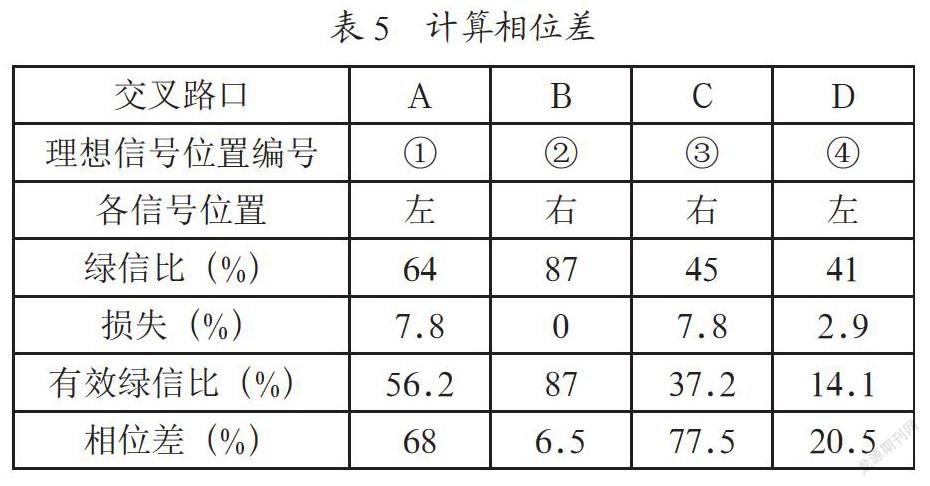
将交叉口A-D经过协调后计算的绿信比填入表5中。绿灯损失等于其最大移动量比上理想位置的距离(即a=102m)表示,如A交叉口的绿灯损失为80/1020=7.8%,列入表5第5行。有效绿信比等于各个交叉口计算出的绿信比与绿灯损失时间的差,列入表5第6行。
可见,四个交叉口之间都采用的是交互式协调方式。相应于奇数理想信号位置的实际交叉口的相位差为100%-0.5*绿信比;相应于偶数理想信号位置的实际交叉口的相位差为50%-0.5*绿信比,将求得的相位差值填入表5第7行。如保持原定周期时长,则系统带速可调整为:V=2*1020/ 109=18.8m/s。
3 绿波协调信号控制方案评价
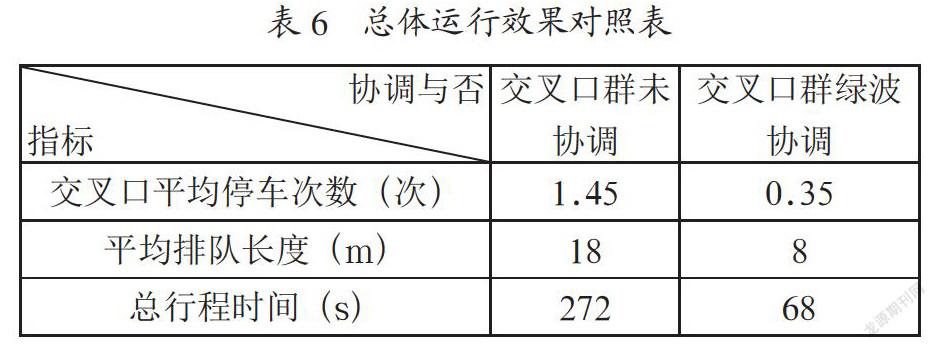
本文采用交通仿真软件VISSIM进行设计对象的交通流仿真,并获取平均停车次数、交叉口平均排队长度以及总行程时间三项指标,进而将未协调与绿波协调的两种情况进行比对,用以评价本文设计的绿波协调方案的效果并进行反馈。具体参数比对见表6。
4 结 论
仿真结果表明,采用本文设计的绿波协调控制方案,能够有效地协调干道交叉口,使车辆在各个交叉口上的延误时间大大地降低,提高通行效率。在保证公交优先的前提下减少了交叉口延误,改善了交叉口服务水平。
参考文献:
[1] 杨晓光,陈白磊,彭国雄.行人交通控制信号設置方法研究 [J].中国公路学报,2001,14(1):73-76.
[2] 翟忠民,景东升,陆化普.道路交通实战案例 [M].北京:人民交通出版社,2007.
[3] 杨浩.运输组织学 [M].北京:中国铁道出版社,2011.
作者简介:唐博(1982.01-),男,汉族,宁夏中宁人,副教授,硕士研究生,研究方向:交通运输、车辆工程。

