基于经验小波变换和Beamlet变换的裂纹检测方法
林哲 蔡恬 王燕锋

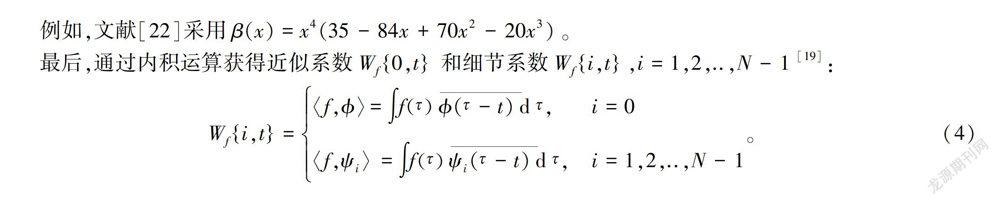




[摘要]在材料完整性检测中,基于计算机视觉的光学检测技术在纹理复杂、噪声较大的背景中准确地检测外部裂纹仍然十分困难。针对这一问题,提出了一种检测裂纹的算法。首先,将裂纹图像自适应地分解为频率分量以得到更好的稀疏表示,然后利用多尺度几何分析技术从重构的近似图像中稳健地提取裂纹的线特征。实验表明,该方法比其他方法能够更准确地检测出图像中的裂纹,在抑制背景纹理和保留裂纹信息这两个性能上取得了较好的综合效果。
[关键詞]裂纹检测;经验小波变换;beamlet变换;稀疏表示
[中图分类号]TP 391.41[文献标志码]A[文章编号]1005-0310(2019)02-0024-08
Abstract: In integrity inspection of materials, the optical detection technique based on computer still has difficulty to detect external cracks efficiently and accurately on the background with complicated texture and noise. To address this problem, an effective method for robustly detecting crack is presented in this paper. It is characteristic that a crack image is decomposed adaptively to frequency components for better sparse representation, and then linear features of cracks are extracted robustly by multi-scale geometric analysis from the approximately reconstructed image. Experiments on various images show that cracks are detected more accurately by using this method than other methods. It achieves a preferable performance on balancing the competing requirements of suppressing background texture and retaining crack information.
Keywords: Crack detection; Empirical wavelet transform; Beamlet transform; Sparse representation
0引言
裂纹检测在土木工程和机械工程的材料完整性检测中发挥着重要作用,基于光学成像的外部裂纹检测技术利用数码相机对材料表面进行成像,然后用计算机算法对图像进行处理以得到裂纹的信息[1-4]。然而,光照条件、光学成像系统等因素对图像质量的影响很大。在噪声干扰或纹理复杂的图像中,准确检测裂纹仍然很困难[5-6]。
Donoho和Huo提出的beamlet变换[7-8]是多尺度几何分析家族[9-13]中的一员,多年来在图像处理中得到了广泛的应用,该算法在噪声背景下提取线特征具有很好的优势。在遥感[14-15]、裂纹检测等领域[16-18],beamlet变换已经得到了成功应用。
为了得到更好的beamlet变换检测结果,本文将经验小波变换(EWT)[19]应用于信号的自适应分析,它根据信号生成特殊的基,以得到更好的稀疏表示。首先,检测信号的傅立叶频谱的局部极大值。然后,每两个相邻极大值取中心点,根据这些中心点将频谱划分多个部分。在此基础上构造了一组小波作为带通滤波器,将细节系数作为信号和经验小波的内积给出,对信号和尺度函数进行内积运算得到近似系数。
文献[20]将经验小波变换推广到二维信号,它可以自适应地对输入图像的傅立叶频谱平面进行分段。在二维张量经验小波变换中,用二维FFT计算图像的傅立叶频谱,在两个方向上取平均值并分别分割。在经验curvelet(曲波)变换中,在伪极坐标FFT[21]计算的傅立叶频谱平面上建立了滤波器组。该滤波器组中的每个滤波器对应傅立叶频谱平面上的一个楔形区域,分别利用各滤波器得到变换系数,为信号提供了更好的稀疏表示。
本文的贡献在于提出了一种有效的方法,利用经验小波变换和beamlet变换改进裂纹检测性能,能够在抑制背景纹理和噪声的同时有效地保留裂纹信息,滤波过程中丢失的有用信息通过beamlet变换的插值和积分得到很好的补偿。本文用多种裂纹图像进行了实验,验证了该方法能够获得更好的检测效果。
1信号的经验分解
经验小波变换(Empirical Wavelet Transform, EWT)是一种将信号自适应分解为频率分量的方法。对于一维离散信号,首先利用傅立叶变换得到傅立叶频谱,然后根据频谱的N个极大值ωii=1,2,…,N定义N-1个边界点Ωi=ωi+ωi+12i=1,2,…,N-1,再根据边界点将傅立叶频谱分割成N个部分,然后构造一组滤波器,其中包含1个低通滤波器和N-1个带通滤波器。
2基于经验小波变换和beamlet变换的裂纹检测方法
材料的断裂过程通常从裂纹萌生开始,小裂纹不断扩展,最终导致完全断裂。显然,裂纹对材料的破坏行为起着至关重要的作用。准确检测裂纹对材料失效的预测和控制具有重要意义,然而,裂纹检测主要有两个难点:
首先,复杂表面对裂纹检测有严重干扰。在大多数情况下,材料的表面可能是粗糙的,很难从表面纹理中分辨出细小的裂纹。
其次,由于材料的非均匀性,裂纹扩展方向非常不规则,没有两个形状完全相同的裂纹。
为解决上述问题,本方法的框架包括3个步骤:
1) 对裂纹图像进行经验分解和稀疏表示,得到不同尺度和角度的低频系数和高频系数,裂纹主要由大系数表示。
对于二维信号(图像) fx,y,将信号的傅立叶频谱平面分解为一组楔形区域,然后检测每一个楔形区域对应的尺度和角度,可以先检测尺度,也可以先检测角度。每个楔形区域ψn,m是径向窗口Wn和极窗口Vm的乘积,并且满足n<Ns和m<Nθ。
文献[20]给出的径向窗口Wn定义如下:
3) 从重建的近似图像中提取线特征。
利用经验小波逆变换以过滤后的系数重建n×n近似图像,然后将它映射到一个方块并进行递归划分。每个方块在每个尺度上都被分割成4个更小的方块,最后,将所有的方块都组织成金字塔结构,每个尺度上的方块可以按行号和列号建立索引。
beamlet字典是不同位置、方向和尺度的线段集合,这些线段被动态地组织起来,能够为多尺度逼近提供基。首先,将一张n×n图像映射成边长为1的方块,并视之为n×n小方块组成的数组0,12。假设n=2j和0≤j≤J,每个方块的每条边都用顶点标注,位于同一条边的两个相邻顶点之间的距离是δ=2-J-K,位于不同边的两个顶点之间的线段为beamlet。
然后,将所有尺度上的beamlet集合构建成beamlet字典。由于beamlet是在每个方块中生成的,它完全覆盖了图像在每个尺度上的所有像素,即在每个区域和方向上提取图像的线特征。沿某一beamlet的像素积分就得到beamlet系数,假设函数f(x1,x2)在[0,1]2上,则连续beamlet变换定义为[7]:
3实验结果
3.1经验小波分解
采用如图1所示的256×256图像作为实验。图2是经验小波分解结果,通过伪极坐标FFT得到傅立叶频谱平面,然后检测极坐标楔形区域的边界,如图2(a)所示。中心是一个圆形区域,即低频分量。此外,还有8个直线边界通过傅立叶频谱的中心点,它们把傅立叶频谱平面的其余部分分成8份。每一部分都由一对对称的楔形区域组成,每一个楔形区域进一步沿径向分割成多个部分。
为了更加明显,将图2(a)对称的楔形区域涂成相同颜色,并用数字标注序号,如图2(b)所示。可以看出,傅立叶频谱平面是根据图像的伪极化FFT结果不均匀分割的,每个楔形区域的徑向分割如表1所示。
3.2裂纹检测
根据公式(8)对系数进行滤波,通过经验小波逆变换得到近似图像,如图4所示。可以看到,在保持裂纹区域完好的情况下,背景纹理受到了明显的压制,这对于下一步准确检测裂纹非常关键。
3.3检测结果对比
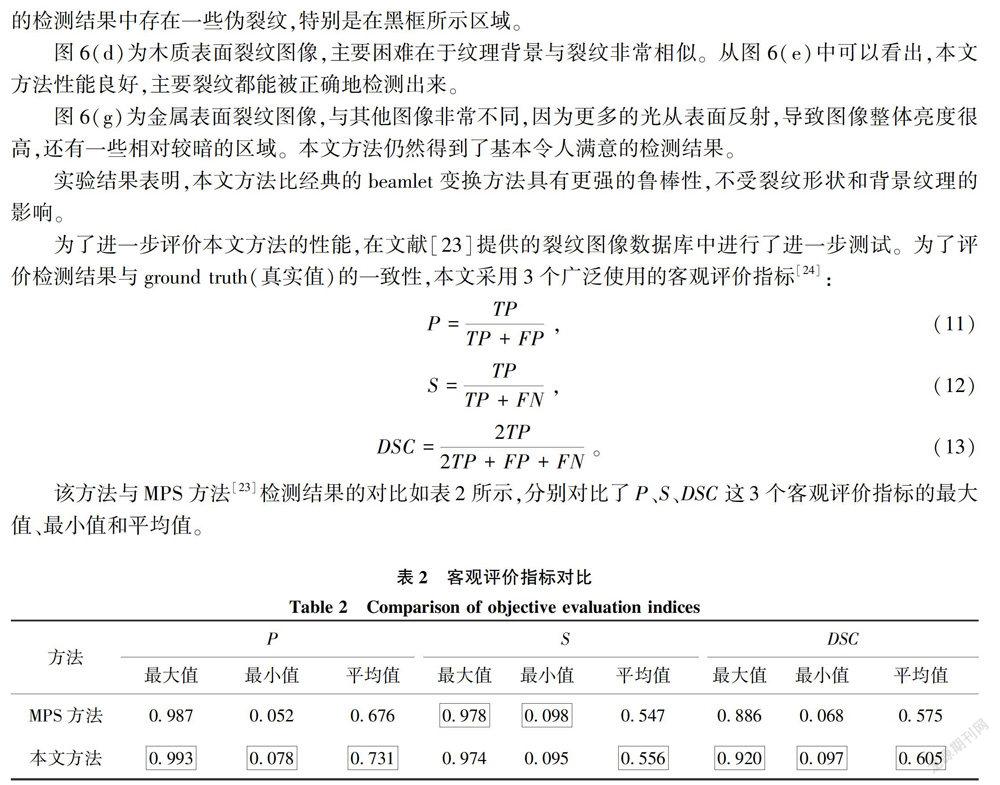
图6(a)为岩石表面裂纹图像,主要的挑战是背景粗糙。从图6(b)和图6(c)的对比可以看出,本文方法优于经典的beamlet变换方法,主要裂纹均能被正确检测出来。从图6(c)中可以看出,经典beamlet变换的检测结果中存在一些伪裂纹,特别是在黑框所示区域。
4结论
本文提出了一种裂纹检测方法,利用经验小波变换对裂纹图像进行稀疏表示,通过系数过滤和经验小波逆变换重构出近似图像,有效地抑制了背景和噪声,最后利用beamlet变换检测裂纹的线特征。
实验表明本文方法能够准确、鲁棒地检测图像中的裂纹,并且不受裂纹形状和背景纹理的影响,取得了较好的综合性能。该方法的主要缺点是分解和重构的步骤占用了太多的时间,为了更加实用,有必要进一步研究提升其计算速度。
[参考文献]
[1]SINHA S K, FIEGUTH P W. Segmentation of buried concrete pipe images[J]. Automation in Construction, 2006, 15(1):47-57.
[2]SINHA S K, FIEGUTH P W. Automated detection of cracks in buried concrete pipe images[J]. Automation in Construction, 2006, 15(1):58-72.
[3]FUJITA Y, HAMAMOTO Y. A robust automatic crack detection method from noisy concrete surfaces[M]. New York:Springer-Verlag New York, Inc. 2011.
[4]ZOU Q, CAO Y, LI Q, et al. CrackTree: Automatic crack detection from pavement images[J]. Pattern Recognition Letters, 2012, 33(3):227-238.
[5]KAUL V, YEZZI A, TSAI Y. Detecting curves with unknown endpoints and arbitrary topology using minimal paths[M]. OakIand,CaIifornia:IEEE Computer Society Press, 2012.
[6]TSAI Y, KAUL V, YEZZI A. Automating the crack map detection process for machine operated crack sealer[J]. Automation in Construction, 2013, 31:10-18.
[7]DONOHO D L, HUO X. Beamlet pyramids: a new form of multiresolution analysis, suited for extracting lines, curves, and objects from very noisy image data[C]// Wavelet Applications in Signal and Image Processing VIII. International Society for Optics and Photonics, 2000:434-444.
[8]DONOHO D L, HUO X. Beamlets and multiscale image analysis[M]//Multiscale and Multiresolution Methods. Berlin: Springer, 2001:149-196.
[9]EMMANUEL J. CANDS, DONOHO D L. Continuous curvelet transform: I. Resolution of the wavefront set[J]. Applied & Computational Harmonic Analysis, 2005, 19(2):162-197.
[10]DONOHO D L. Wedgelets: nearly minimax estimation of edges[J]. The Annals of Statistics, 1999, 27(3):859-897.
[11]PENNEC E L, MALLAT S. Sparse geometric image representations with bandelets[J]. IEEE Transactions on Image Processing, 2005, 14(4):423-38.
[12]MALLAT S. Geometrical grouplets[J]. Applied & Computational Harmonic Analysis, 2009, 26(2):161-180.
[13]LIN Z, YAN J, YUAN Y. Algorithm for image fusion based on orthogonal grouplet transform and pulse-coupled neural network[J]. Journal of Electronic Imaging, 2013, 22(3):033028.
[14]ZHU Y, SALARI E. Extraction of linear features based on beamlet transform[C]// IEEE International Conference on Electro/information Technology. IEEE, 2011.
[15]YING L, SALARI E. Beamlet transform based technique for pavement image processing and classification[C]// IEEE International Conference on Electro/information Technology. IEEE, 2009.
[16]WEI N, ZHAO X M, DOU X Y, et al. Beamlet transform based pavement image crack detection[C]// International Conference on Intelligent Computation Technology & Automation. IEEE, 2010.
[17]ZHAO G, WANG T, YE J. Surface shape recognition method for crack detection[J]. Journal of Electronic Imaging, 2014, 23(3):033013.
[18]LIN Z, YAN J, YUAN Y. Target detection for SAR images based on beamlet transform[J]. Multimedia Tools and Applications, 2016, 75(4):2189-2202.
[19]GILLES J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16):3999-4010.
[20]GILLES J, TRAN G, OSHER S. 2D empirical transforms. Wavelets, ridgelets and curvelets revisited[J]. SIAM Journal on Imaging Sciences, 2014, 7(7):157-186.
[21]AVERBUCH A, COIFMAN R R, DONOHO D L, et al. Fast and accurate Polar Fourier transform[J]. Applied & Computational Harmonic Analysis, 2006, 21(2):145-167.
[22]DAUBECHIES I. Ten lectures on wavelets[M]. Philadelphia,Pennsylvania: Society For Industrial and Applied Mathematics, 1992.
[23]AMHAZ R, CHAMBON S, IDIER J, et al. Automatic crack detection on two-dimensional pavement images: an algorithm based on minimal path selection[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(10):2718-2729.
[24]SAMPAT M P, WANG Z, GUPTA S, et al. Complex wavelet structural similarity: a new image similarity index[J]. IEEE Transactions on Image Processing, 2009, 18(11):2385-401.
(責任编辑白丽媛)

