采用改进神经网络PID控制的车辆悬架振动仿真研究
孙 亮
(池州职业技术学院机电系,安徽,池州 247000)
0 引言
当车辆在路面上行驶过程中,由于路面各种激励信号会通过轮胎传递给车辆悬架,导致车辆发生振动现象,从而影响到驾驶员乘坐的舒适性。传统车辆悬架减震器响应时间较长,不能适应复杂路况,有可能造成人员受伤。导致这一现象的主要原因还是车辆悬架装置控制不当。目前,市场上大多车辆采用的是被动悬架,被动悬架阻尼系数和刚度系数通常是固定的,不能进行实时调整[1]。主动悬架在被动悬架基础上增加了自适应调节控制系统,可以通过主动控制实现多目标控制[2]。
当前,人们对车辆舒适度要求越来越高,因此,许多科研人员对车辆悬架系统进行了深入研究。例如:文献[3]采用改进PID控制车辆悬架系统,分析了车辆悬架系统参数,引用传统PID控制器,采用粒子群算法优化PID控制参数,通过车辆振动仿真检验优化后的控制效果,从而改善了车辆悬架性能。文献[4]采用PID控制汽车悬架系统,创建主动悬架简图,根据动力学定理建立振动数学模型,设计主动悬架PID控制系统,采用MATLAB软件对车辆振动评价指标参数进行仿真,从而提高了车辆控制响应速度。文献[5]采用 RBF神经网络控制车辆主动悬架系统,建立了主动悬架系统模型,在传统PID控制基础上,设计了RBF神经网络PID控制器,采用MATLAB软件RBF神经网络PID控制效果进行仿真验证,从而降低了车辆振动幅度。以往研究的车辆主动悬架控制系统,在一定程度上降低了车辆振动幅度,但是受到路面激励信号干扰时,振动幅度仍然较大。对此,本文创建了1/4车辆2自由度的车辆悬架模型,根据牛顿定律推导车辆悬架振动方程式,引用BP神经网络PID控制车辆主动悬架,采用改进粒子群算法优化BP神经网络PID控制器。通过数学软件MATLAB对车辆振动评价指标参数进行仿真,与优化前形成对比和分析,为深入研究车辆主动悬架控制系统提高参考依据。
1 车辆悬架模型
为了简化车辆悬架研究模型,采用1/4车辆2自由度模型为研究对象,如图1所示。
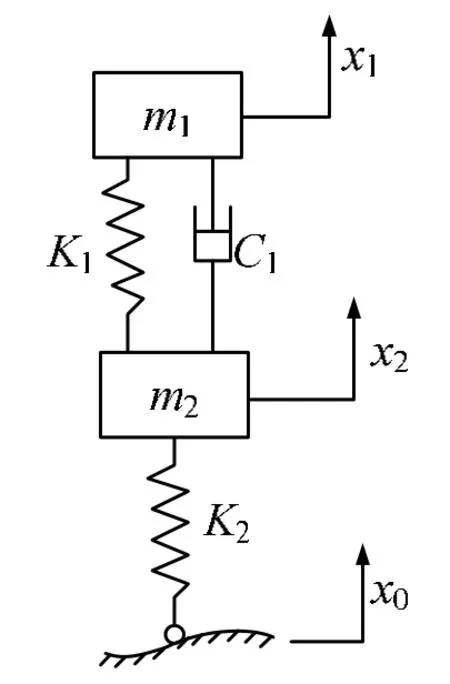
图1二自由度车辆被动悬架简图Fig.1 A sketch of two-degree-of-freedom vehicle passive suspension
根据牛顿定律可知,悬架振动方程式[6-7]为:
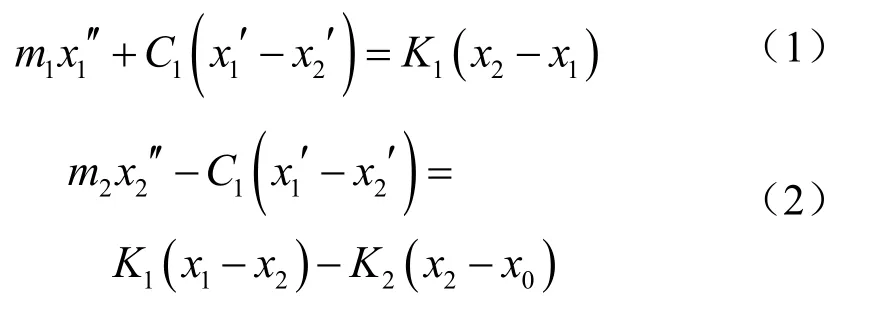
式中:m1为车身质量;m2为车轮质量;K1为悬架刚度;K2为轮胎刚度;C1为减震器阻尼系数;x0为路面噪声激励函数;x1车身位移;x2为轮胎位移。
2 神经网络PID控制器
神经网络PID控制器采用增量式数字PID控制器和BP神经网络,其控制结构如图2所示。
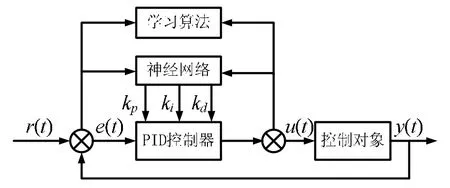
图2神经网络PID控制器Fig.2 Neural network PID controller
PID控制采用增量式,其方程式[8]为:
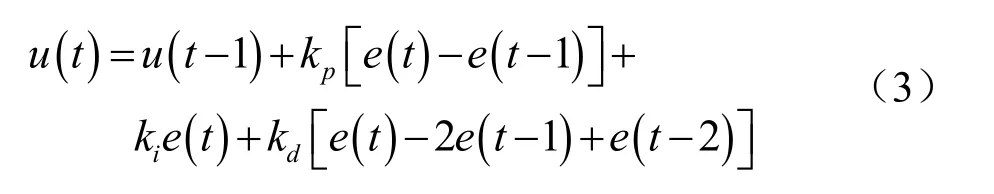
式中:kp为比例系数;ki为积分系数;kd为微分系数;e(t)为误差。
神经网络采用三层BP结构,如图2所示。
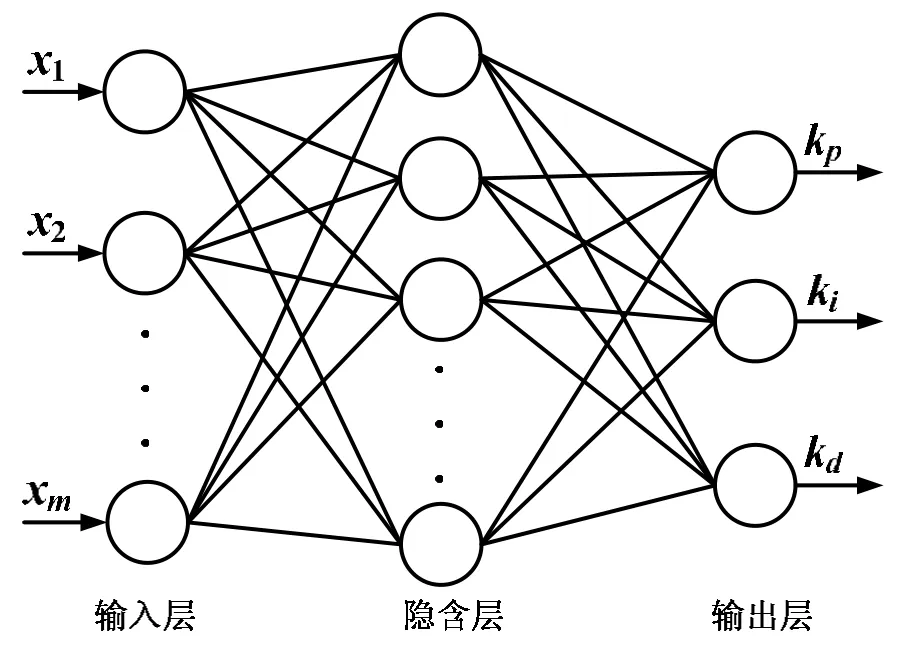
图3 三层BP神经网络Fig.3 Three-layer BP neural network
在图3中,假设输入层节点有m个,隐含层节点有Q个,输出层有3个节点。
输入层网络结构[9]为:

隐含层输入和输出网络结构[9]为:
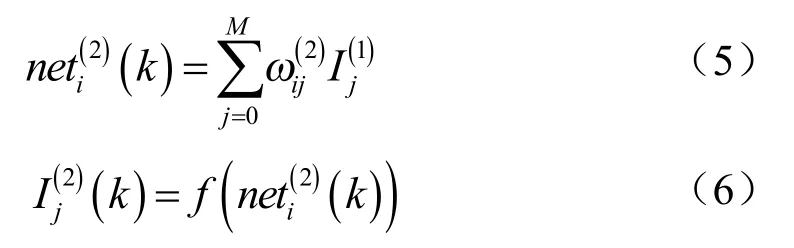
隐含层采用双曲正切函数,如下所示:

输出层输入和输出网络结构[9]为:
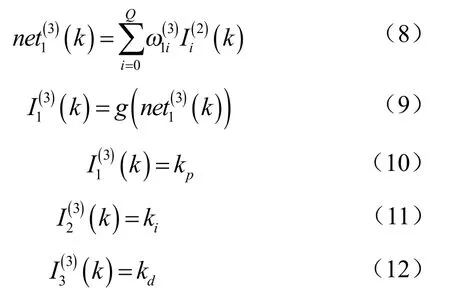
增量式PID控制器调节参数kp、ki和kd对应神经网络3个输出节点。输出层激活函数采用非负函数,如下所示:

控制器性能目标函数为:
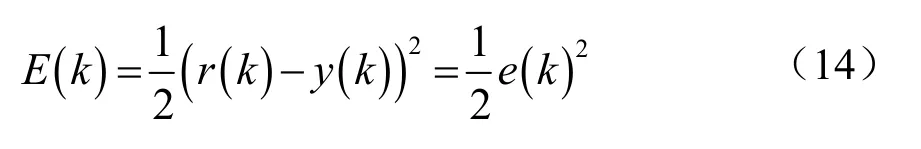
3 改进BP神经网络PID控制
3.1 改进粒子群算法
粒子群算法和模拟退火算法类似,从随机解开始,通过迭代更新搜索出全局最优解。粒子在迭代搜索过程中,其速度和位置更新方程式[10-11]为:
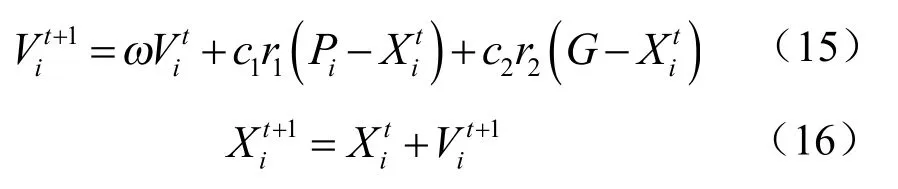
式中:为粒子i迭代t次的速度;为粒子i迭代(t+1)次的速度;c1和c2为区间[0,2]的学习因子;r1和r2为区间[0,1]的随机数;ω为惯性权重系数;Pi为粒子i个体最优位置;G为种群中最优位置;为粒子i迭代t次的位置;为粒子i迭代(t+1)次的位置。
为了提高粒子群算法优化能力,对粒子群算法惯性权重系数和变异操作进行改进,惯性权重系数改进公式为:
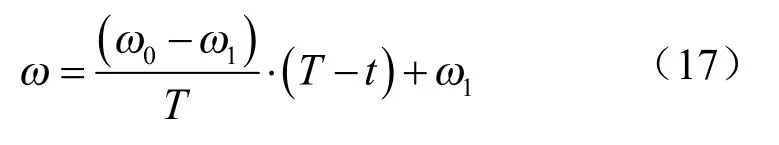
式中:ω0为初始惯性权值;ω0为最终惯性权值;t为当前迭代次数;T为最大迭代次数。
变异操作是对粒子位置更新后,重新初始化更新粒子,通过迭代搜索到全局最优值。粒子群算法加入变异操作,全局最优值搜索能力更强,自适应变异操作公式为:
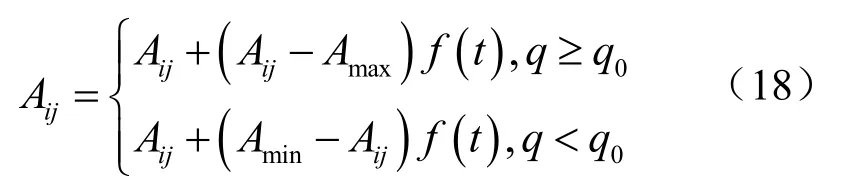
式中:Amax、Amin为粒子Aij的上限和下限;r为区间[0,1]的随机数;a为可调参数。
3.2 改进神经网络PID控制优化
采用改进粒子群算法优化神经网络,优化目标是适应度函数。改进粒子群算法搜索到全局最优位置时,其适应度函数值最小。适应度函数选择车身加速度均方根值,其计算公式为:

适应度函数值越小,悬架振动幅度越小,控制效果越好。车辆振动采用改进粒子群算法优化 BP神经网络控制流程如图4所示。具体控制过程如下:
1)计算输出信号与输入信号误差;
2)将误差反馈后,通过粒子群算法对神经网络初始权值进行训练;
3)通过训练后获得最佳权值,通过优化后的神经网络在线调节PID控制参数,输出最优PID控制参数。
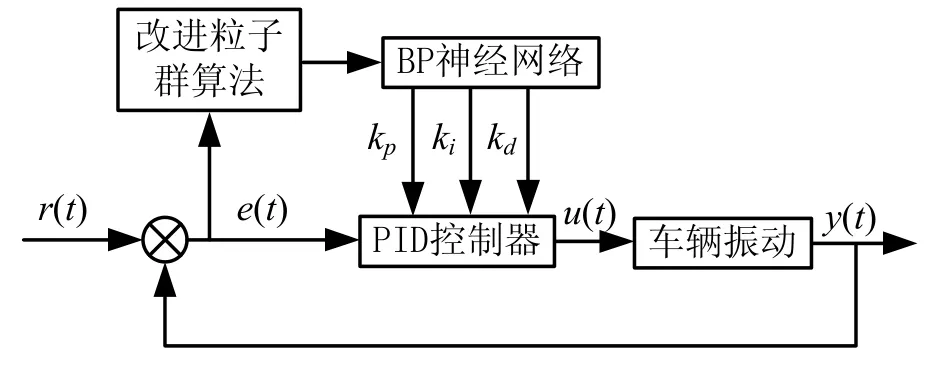
图4 车辆振动控制优化流程Fig.4 Optimized flow of vehicle vibration control
4 仿真及分析
为了对比不同控制器控制效果,假设路面为白噪声激励信号,其公式[12]为:
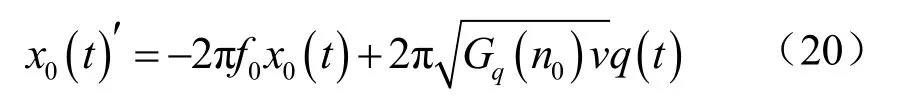
式中:f0为振动频率;Gq(n0)为路面不平度系数;v为车辆行驶速度;q(t)为高斯白噪声。
为了验证改进粒子群算法优化 BP神经网络PID控制效果,采用MATALB软件对车辆振动进行仿真验证。车辆振动仿真参数设置为:m1=350 kg,m2=45 kg,K1=17000 N/s,K2=200000 N/s,C1=1500 Ns /m,振动频率f0=0.1Hz,初始种群数量为30,最大迭代次数为100;惯性权重系数为ω0=0.9,ω1=0.4,学习因子为c1=c2=2,随机数为r1=r2=0.5,神经网络学习速率为0.25。假设车辆行驶速度为30 m/s,通过白噪声路面激励信号后,车身加速度、悬架行程及轮胎位移仿真结果如图5、图6及图7所示。
根据图5可得:采用BP神经网络控制器,车身加速度的均方根值较大;而采用改进BP神经网络控制器,车身加速度的均方根值较小。根据图6可得,采用BP神经网络控制器,车辆悬架悬架行程均方值较大;而采用改进BP神经网络控制器,车辆悬架悬架行程均方值较小。根据图7可得:采用BP神经网络控制器,车身位移均方根值较大,而采用改进BP神经网络控制器,车身位移均方根值较小。分析图5-图7仿真结果可知,采用改进粒子群算法优化BP神经网络控制器,车身加速度、悬架行程和轮胎位移的均方根值都大幅度下降,降低悬架上下振动幅度,改善驾驶员乘坐舒适性。
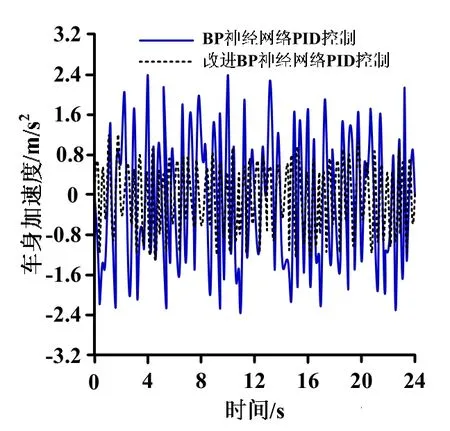
图5 车身加速度仿真结果Fig.5 Simulation results of body acceleration
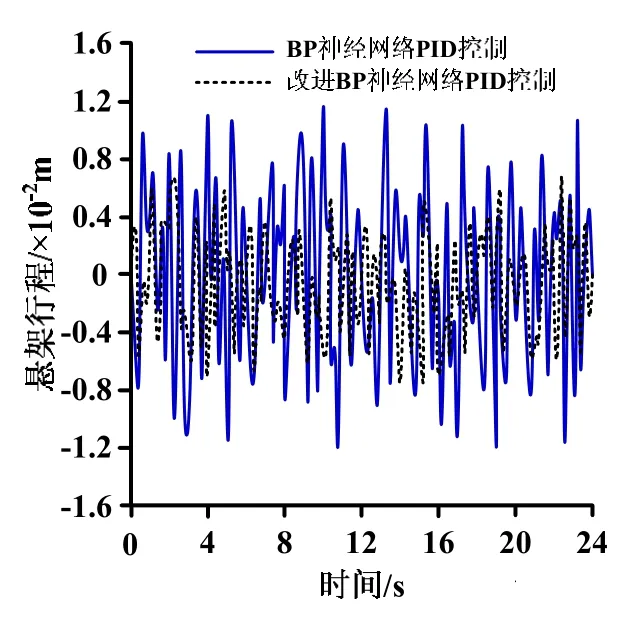
图6 悬架行程仿真结果Fig.6 Simulation results of suspension travel
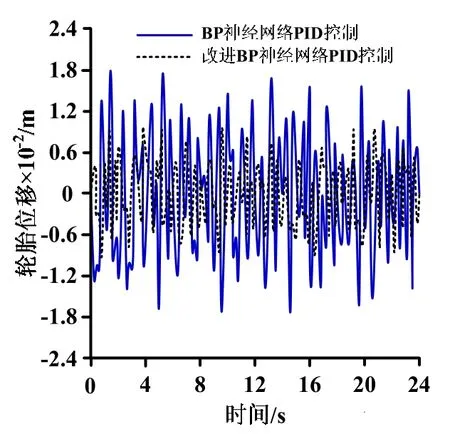
图7 轮胎位移仿真结果Fig.7 Simulation results of tire displacement
5 结语
本文研究了1/4悬架平面简图模型,推导出车辆悬架振动微分方程式。引用增量式PID控制器,采用BP三层神经网络结构,设计出神经网络PID控制器,构造出全局最优值适应度函数。对传统粒子群算法进行改进,将改进粒子群算法优化BP神经网络结构,采用 Matlab 软件对车辆悬架参数进行仿真,并且神经网络PID控制器进行对比和分析。仿真结果显示:优化后,车辆垂直速度、悬架行程及车辆位移峰值下降,整体波动幅度较小。改进神经网络PID控制器能够提高车辆行驶的稳定性,避免车辆发生侧翻现象。

