考虑温度效应的花岗岩分数阶蠕变模型研究

(成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

温度是影响岩石物理力学性质的重要外因之一，尤其是对高放射性核废料处理等工程有较大影响。由温度导致的岩石力学性质的变化规律是当前岩石力学界研究的一个焦点问题。探究并获得宏观可用的考虑温度变化的岩石蠕变模型对于指导岩石工程建设具有重要意义。

目前，温度导致岩石蠕变行为机理的研究已得到诸多研究者的关注。Chan K S等[1]提出了一种考虑损伤断裂的盐岩蠕变模型，并通过蠕变试验数据验证了模型合理性；郤保平等[2]进行了层状盐岩蠕变特性试验，建立层状盐岩的稳态蠕变率本构方程；高小平等[3]对不同温度处理后的盐岩蠕变特性进行研究，得到了岩石稳态蠕变率本构方程；周广磊[4]等建立了温度-应力耦合作用下脆性岩石时效蠕变损伤模型，并在COMSOL的基础上进行二次开发，给出了温度-应力耦合作用下岩石时效蠕变损伤模型的数值求解方法；陈亮[5]等利用三维声发射实时监测信息，开展北山花岗岩的蠕变变形特征以及加载条件对其蠕变破坏过程的影响研究；杨春和[6]等给出了一个反映盐岩蠕变全过程的非线性蠕变本构方程；朱昌星[7]等在非线性黏弹塑性流变模型的基础上，根据时效损伤和损伤加速门槛值的特点，建立了非线性蠕变损伤模型，并通过对板岩进行试验研究，验证了模型的合理性；丁靖洋等[8-9]基于分数阶微分理论，利用变黏性系数Abel黏壶替代西原正夫模型中Newton黏壶的方法，建立了盐岩蠕变损伤本构模型。

由以上论述可知，在建立反映温度影响的蠕变模型时，常有两种代表性的做法：① 通过热力学理论中关于能量损伤的办法解决；② 一种经验方法，即通过拟合蠕变参数随温度变化的关系，而后再代入蠕变模型中。相比之下，第一种方法的理论性更高，第二种做法则更为简单。而在岩石力学界，后者仍然是一种通用的研究手段。相应的，采用后者时，蠕变本构的选取对最终结果影响性较大，因而采用合理的蠕变模型尤为重要。本文采用后者建立花岗岩的温度-蠕变耦合模型。基于已被广泛认可的分数阶蠕变模型，分析蠕变参数随温度的变化，然后获得岩石温度蠕变耦合模型，并对其模型参数展开详细的讨论。

1 不同温度下花岗岩的蠕变特性

刘泉声等[10]进行了不同温度下花岗岩的蠕变试验。采用岩芯钻取法将试件加工成直径为50 mm，高度为100 mm的圆柱体。试验过程中，将三轴室的温度按2℃/min的速率升至所需的温度，保持该温度4 h后开始加载试验。在温度T=20 ℃，60 ℃，80 ℃，100 ℃，200 ℃，300 ℃条件下，保持轴向应力为120 MPa，对三峡花岗岩进行了一系列的单轴抗压蠕变试验。试验结果如图1所示。

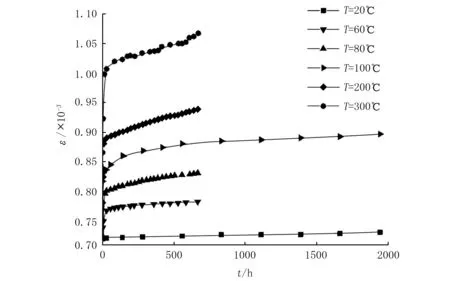
图1 不同温度下花岗岩的蠕变试验曲线[8]Fig.1 Creep curves of granite under different temperatures

由图1可以看出：在同一时间段，随着温度的升高，瞬时应变不断增加。若以弹性模量为研究对象，就会发现随着温度的上升，瞬时的弹性模量值会随之减小；在相同的轴向应力作用下，应变率也随着温度的增长而增加[11]。

2 分数阶蠕变模型

2.1 分数阶微积分

分数阶微积分有多种定义。现采用最常见的Riemann-Liouville分数阶微积分定义方法。先给出分数阶积分定义[12]：设f在(0，+∞)上连续且属于(0，+∞)的任何有限子区间内都可积，由t>0，有Re(γ)>0，此时可得出：

(1)

式(1)即为函数f(x)的β阶分数阶积分，其中，Γ(β)为Gamma函数。

2.2 分数阶蠕变元件

由上述分数阶微积分的定义，将其引入到花岗岩蠕变本构模型构建之中。其本构关系如下：

σ=ηdβε(t)/dtβ0≤β≤1

(2)

式中，η为黏性系数。

令σ为一常数σ0，此时将式(2)两边都进行分数阶积分。可描述蠕变行为的表达式如下：

(3)

此时，该元件即为Newton黏壶，代表理想流体； 当β=0时，该元件变为弹簧元件，代表理想弹性体。可见，分数阶蠕变元件是一种可以用来模拟介于理想流体与理想弹性体之间的材料模型[13-15]。

2.3 蠕变模型的建立

分数阶黏弹塑性蠕变模型如图2所示。

图2 蠕变本构模型示意Fig.2 A schematic diagram of creep constitutive model

由图2可知，此时若令总应变为ε，塑性体的应变为εvp，分数阶蠕变元件应变为εve，胡克体的应变为εe，继而可得出总应变的表达式如下：

ε=εe+εve+εvp

(4)

现分别表述图2中当总应力为σ时各元件的应力应变关系。

(1) 胡克体：

(5)

式中，E0为胡克体中弹簧的弹性模量。

(2) 分数阶蠕变元件：

σ=η0dβεve(t)/dtβ

(6)

(7)

(3) 黏塑性体中，摩擦滑块应力σp的值则是根据总应力与屈服应力的大小来决定的，即

(8)

式中,σs为屈服应力。

根据元件串、并联理论，可得出总应力与弹性体的应力和摩擦滑块应力之间的关系如下：

σ=σd+σp

(9)

式中,σd为分数阶蠕变元件的应力。

当σ<σs时，由式(8)和(9)可得σd=0，即

εvp=0

(10)

当σ≥σs时，结合式(9)，可得本构关系：

η1dγεvp(t)/dtγ+σs=σ

(11)

(12)

式中,η1为黏塑性体中Abel黏壶的黏性系数，γ为其求导阶数。

由初始条件t=0时εvp=0，求解式(12)可得：

(13)

即

(14)

综上所述，分数阶黏弹塑性蠕变模型的本构方程可表示为

(15)

3 本构模型的验证及参数分析

现将图1中不同温度对应不同时刻的应变值提取出来，代入式(15)。用差分进化法拟合得到不同温度下参数E0、η0以及β的取值(见表1)。

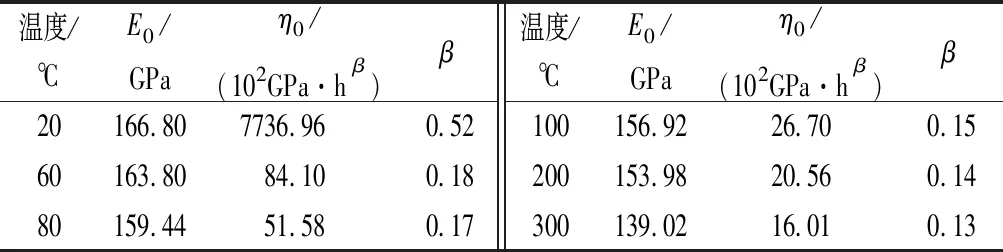
表1 弹性模量、黏性系数和求导阶数随温度的变化Tab.1 Variation of elastic modulus, viscosity coefficient and derivation order

拟合结果与试验结果之间的吻合度较好，说明拟合得到的参数值较为合理。

将表1中的E0、η、β分别与温度T进行拟合，拟合结果如图3所示。最终可以得到花岗岩不同时间段、不同温度下的ε值。

由图3可知，无论是弹性模量E0、黏性系数η0，还是求导阶数β，都是随着温度的上升而呈现减小的趋势。对E0而言，根据其物理意义，在保持轴向应力不变的基础上，温度持续增加，应变会呈现线性增长的趋势。3种参数的拟合结果如下：

E0=-91.197T+167980

(16)

η0=1.23098×1011·T-3.99813

(17)

(18)

将式(16)、(17)、(18)联立代入式(15)可得：

(19)

式(19)即为考虑温度效应的蠕变方程，可作为花岗岩蠕变研究的一个参考。

4 分数阶蠕变模型参数分析

为研究各参数对蠕变模型的影响规律，采用控制变量的方法，分别对弹性模量E0、黏性系数η0和求导阶数β进行分敏感性分析。模型参数取值：σ=120 MPa，E0=145 GPa，β=0.25，η0=65 GPa·h0.25。

4.1 弹性模量

分析弹性模量时，黏性系数η0和求导阶数β保持不变，可得到不同E0状态下的蠕变曲线。由图4可知，E0决定了瞬时蠕变强度以及整体蠕变强度。随着时间的增加，应变率基本不变；随着E0的降低，达到同一应变值的时间逐渐增加。这表明在蠕变的前两个阶段，较小的E0值，会缩短从加速蠕变到稳态蠕变的时间，但对蠕变的整体趋势影响较小。

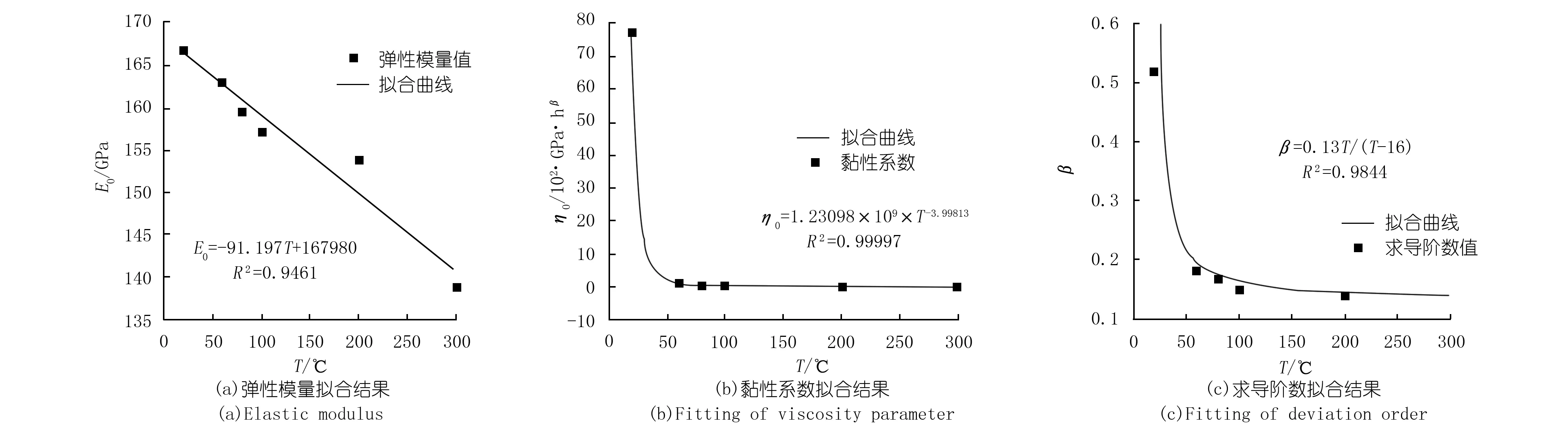
图3 参数拟合结果比较Fig.3 Comparison of the fitting parameters

图4 弹性模量变化值对应变的影响Fig.4 The influence of change elastical of modulus on strain

4.2 黏性系数

分析黏性系数时，弹性模量E0和求导阶数β保持不变。图5可知，随着η0的增加，花岗岩进入稳态蠕变的时间大幅降低，且当η0值增加幅度较大时，这种现象尤其明显。此外，从瞬态蠕变过渡到稳态蠕变的时间也会大大缩短。

图5 黏性系数值对应变的影响Fig.5 The influence of the viscosity value on strain

4.3 求导阶数

保持弹性模量、黏性系数不变，改变求导阶数，得到不同求导阶数下岩石蠕变曲线。由图6可知，无论β如何取值，初始蠕变值均为一定值，即β对初始瞬时蠕变值影响较小，但对最终蠕变值的影响较大。当β较小时，应变速率较低，加速蠕变阶段不明显，且更容易达到稳定蠕变阶段。

综上所述，弹性模量对花岗岩蠕变强度的变化起主要作用，却并不影响总体蠕变趋势。就黏性系数与求导阶数而言，在温度影响下，随着参数值的降低，黏性系数会增加岩石进入稳态蠕变的时间，后者则恰恰相反。综合来看黏性系数影响较大。

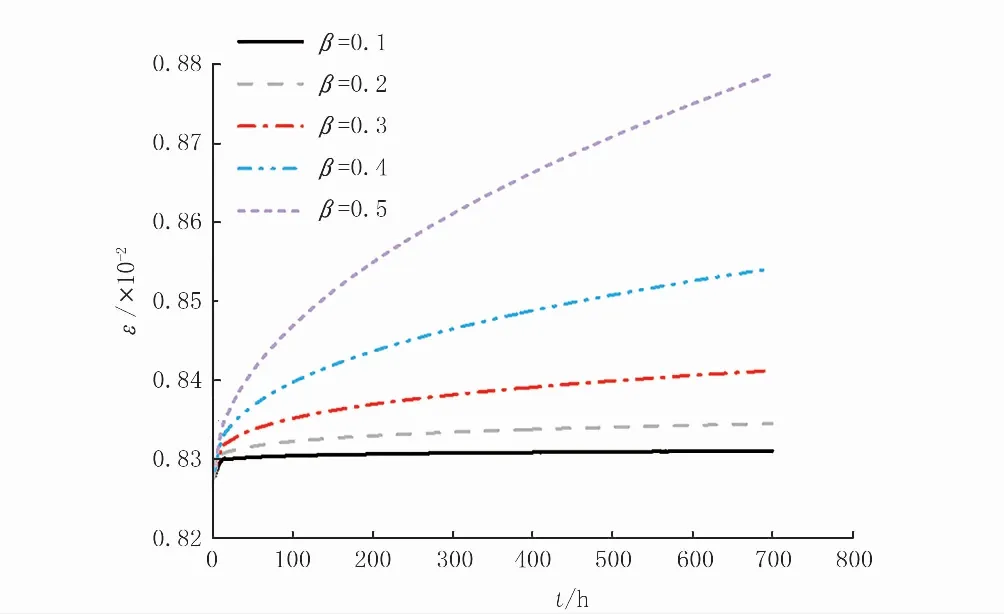
图6 求导阶数值对应变的影响Fig.6 The influence of derivation order value on strain

5 结 论

(1) 根据分数阶黏弹塑性蠕变模型拟合不同温度下岩石蠕变试验结果，获得了考虑温度效应的蠕变方程，对类似高放射性废物的处置工程等提供了参考。

(2) 对分数阶黏弹塑性蠕变模型的蠕变参数进行了敏感性分析，揭示了该模型参数对蠕变的影响规律。研究表明：温度的上升导致蠕变参数值减小，其中弹性模量与黏性系数的值均与花岗岩到达稳态蠕变阶段的时间呈负相关关系，而求导阶数值则相反。