装药结构对深水钻孔爆破效果的影响分析

胡 伟 才1，张 晓 强，郭 铭 芳1，彭 高 峰1，吴 立

(1.长江重庆航道工程局，重庆 400011； 2.中国地质大学(武汉) 工程学院，湖北 武汉 430074)

水下爆破是一种在水下岩石等结构物上钻孔并用炸药填充，充分利用爆炸的猛度及所产生的爆生气体对岩石进行破碎的爆破方法。该方法已广泛应用于桥墩基坑开挖[1-2]、航道炸礁等领域[3-4]，已成为现代水下工程爆破的主要方法。受深水压力的影响，通常情况下要达到相同的爆破效果，水下爆破所用药量要大于陆上爆破。采取合理的装药结构，延长爆破作用时间，以提高炸药能量利用率并降低炸药单耗，是目前水下爆破亟待解决的一项重要课题。

目前，常用且有效的水下爆破效果提升方式是对不耦合装药的耦合介质、耦合系数进行优化。钟明寿等通过MATLAB编程计算了不同耦合介质装药结构炮孔孔壁爆炸载荷和透射比能的时间函数，得知水不耦合装药时孔壁透射比能量最大[5]；程俊飞等根据固液气三相爆破计算模型分析了爆轰炮孔内压随时间的变化、围岩应力场随时间和空间的变化情况以及裂纹尖端应力强度因子，发现水不耦合装药爆破能延长炮孔内压的作用时间[6]；徐颖等从理论上分析装药不耦合系数与爆破作用的关系,并在实验室和现场进行了部分试验,得出了不耦合系数为1.67时的爆破裂纹长度最长的结论[7]；王志亮等基于HJC模型对水不耦合装药爆破中不同径向耦合系数展开了对比数值计算，综合分析了损伤破坏区分布和孔壁压力、加速度以及速度等与径向不耦合系数间的关系[8]。尽管有不少学者在优化不耦合装药结构、提升爆破效果等方面进行了研究，但大多数针对的是单因素影响下的浅水及陆上不耦合装药爆破效果优化。而对于水深大于30 m的深水条件下的水下爆破，爆破环境复杂、技术要求高、施工难度大，与浅水爆破相比，深水爆破理论研究比较滞后。由于爆破过程具有瞬时性、模糊性和多样性等特点，整个过程涉及炸药和周围岩石介质及炮孔填塞物等在高速碰撞、爆炸和高压等大变形动力下的响应[9-10]，通过一般的数学方法求解十分困难。因此，本文利用广泛使用的成熟数值模拟软件ANSYS/LS-DYNA[11-14]对30 m深水条件下单孔爆破的破岩过程进行了模拟再现，从耦合介质以及不耦合系数两个因素角度综合考虑，通过正交模拟试验分析了不耦合装药结构下的爆破效果，以期为深水条件下的水下钻孔爆破施工提供理论参考。

1 计算模型与参数

1.1 工程背景

三峡-葛洲坝两坝间莲沱河段位于湖北省宜昌市夷陵区，属于长江干线上游河段，全长约6.5 km。炸礁整治工程的重难点区域为梳子溪晒经坪左岸水下河床炸礁LT7炸礁区。该区域爆破厚度大、爆破开挖水深大，爆破岩层平均厚度为11.6 m，最大厚度超过23 m。炸礁区河床底高在30.1～53.5 m之间，最大施工水深达37 m。水下炸礁工程量651 176.2 m3，水下清渣工程量612 105.6 m3。

1.2 模型及基本参数

为了考察不同装药结构下爆破对岩石介质的破坏作用，结合工程实例设炮孔孔径为80 mm。建模时，为节省计算量，利用模型的对称性，取1/4模型作为研究对象，建立尺寸为1.5 m×1.5 m×37 m的模型，其中水层厚度30.0 m，炮孔直径80 mm。孔口和两段装药之间的填塞介质均为碎石，孔口填塞长0.8 m，如图1所示(图中省略30 m厚水层)。起爆点都设在炸药底部。为进行对比，在建立模型时固定两种情形下水、填塞、炸药和岩石的网格尺寸和形式。计算边界条件为：炮孔轴线所在的两相邻平面为对称边界，水上部为自由边界，其余为透射边界。考虑到爆炸持续时间，求解时间设置为30 000 μs，计算过程中每隔100 μs输出一步结果文件，数值模型采用cm-g-μs单位制。模型中含有水、填塞、炸药和岩石4种材料，炸药和水采用Euler单元网格，岩石和填塞采用Lagrange单元网格，模型采用ALE流固耦合算法[15-17]。

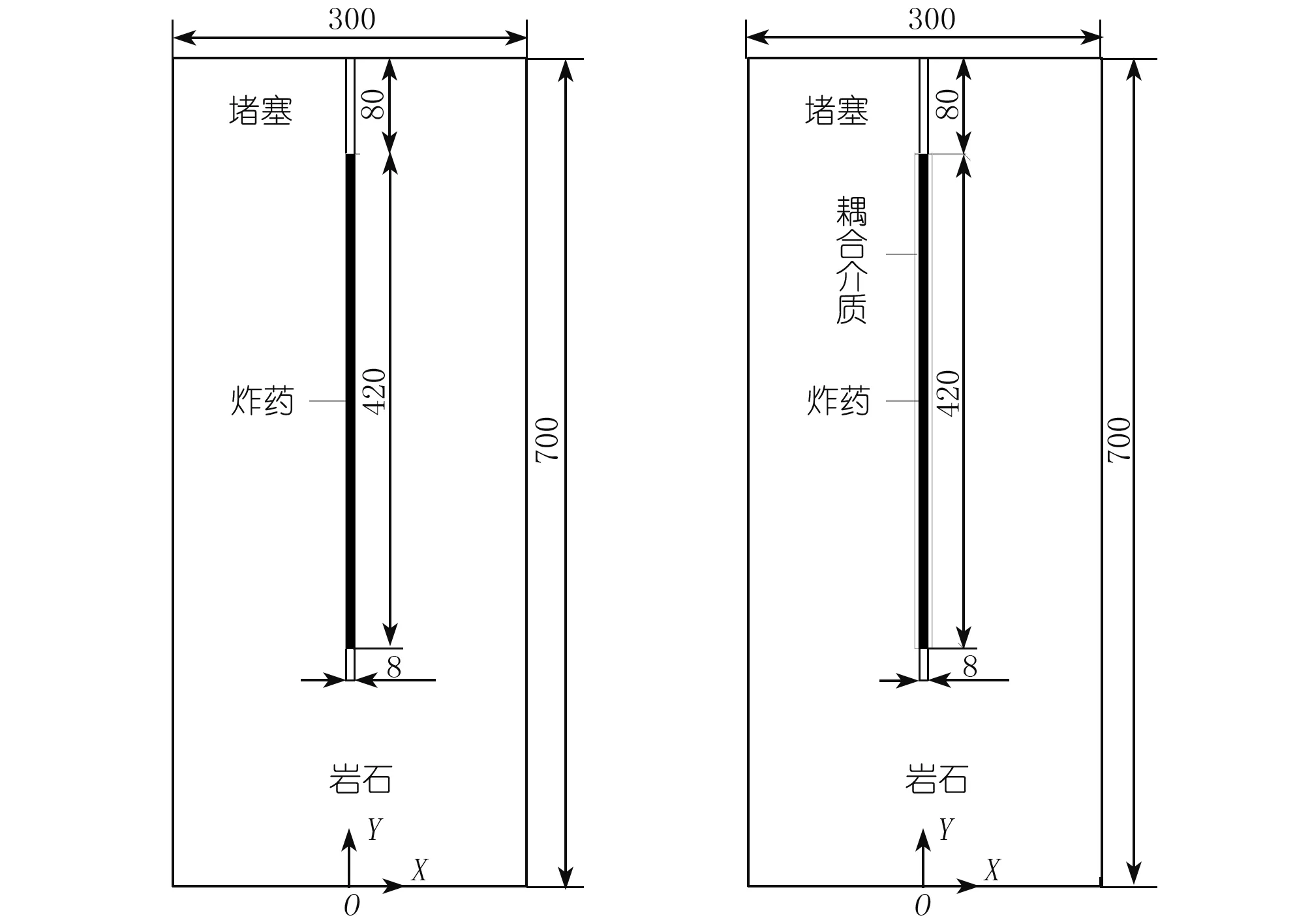
图1 计算模型示意(单位：cm)Fig.1 Schematic diagram of calculation models

1.3 岩石模型及参数

岩体是一种非连续、非均质、各向异性并且带有不同缺陷的流变介质，很难进行定量分析[18]。严格来说，线弹性模型只能描述岩土介质的初始变形，而在爆炸荷载作用下，被爆岩石先出现弹性变形后出现塑性变形。为了合理地描述岩石变形及破坏规律，本文选用与工程实际具有很好契合度的弹塑性模型[19-20]。该模型考虑了材料的弹塑性性质，并且能够对材料的强化效应(随动强化和各向同性强化)和应变率变化效应加以描述，同时带有失效应变，岩石材料物理力学参数见表1。

表1 岩石材料物理力学参数Tab.1 Physical and mechanical parameters of rock material

1.4 炸药模型和状态方程

在数值模拟中，精确描述装药爆轰时的压力变化历程对最终的数值计算结果非常重要，本文采用LS-DYNA手册[21]中提供的高能炸药材料和JWL状态方程描述整个爆腔的动力膨胀。JWL方程定义压力为相对体积和内能的函数，能精确描述爆炸过程中爆轰产物的压力、体积、能量特性，一般表现为如下形式：

(1)

式中，A、B、R1、R2、ω均为输入参数；V为炸药相对体积；E0为炸药内能。本次数值模拟采用的是2号岩石乳化炸药，其密度为1 610 kg/m3，爆速为4 500 m/s(见表2)。

表2 2号岩石乳化炸药参数Tab.2 Parameters of No.2 rock emulsion explosive

1.5 水材料模型及参数

本文采用Gruneisen状态方程来描叙水的各项物理力学特征，水的状态方程如式(2)所示。

(γ0+αμ)E0

(2)

式中,P为压力；E0为单位体积的初始内能；ρ为材料密度；ρ0为材料初始密度；C为vs-vp曲线截距；γ0为Gruneisen常数项；α是γ0和μ的一阶体积修正量；S1、S2、S3为与vs-vp曲线斜率相关的参数。各项参数取值见表3。

表3 水的状态方程参数Tab.3 State equation parameters of water

2 模型验证

为更好地体现后续不耦合装药正交模拟试验的合理性，建立耦合介质为水，不耦合系数为1.2的单孔不耦合装药数值模型，获取炮孔上方轴线方向水中一系列测点的冲击波压力峰值，结果如表4所示。

通过Origin软件对不同测点水中冲击波压力峰值数据进行非线性拟合，可得到水中冲击波压力峰值与距炮孔口部不同距离之间的关系式：

现场实测。

P=21.64L-1.114；R2=0.9303

(3)

模拟计算：

P=23.15L-1.148；R2=0.9527

(4)

对比现场实测曲线与数值模拟计算曲线，结果如图2所示，为便于区分两种结果的误差，纵坐标采用对数刻度。

由式(3)～(4)及图2可知，应力波的峰值压力随着距离的增大总体上呈指数衰减趋势，在近区的1～3 m内衰减较快，而3 m以后远区的峰值压力衰减速度逐步降低。同时，从曲线可以看出，对于同一测点的峰值压力数据，实测结果与数值模拟结果误差较小，平均误差为11.29%，整体衰减趋势一致，验证了模型各项参数的正确性，可进一步用于正交模拟试验。

表4 距炮孔口部不同距离测点的压力峰值Tab.4 Peak pressure of monitoring site with different distance from blast hole

3 正交模拟试验

3.1 构造正交试验表

选择L9正交表来构造试验方案，分别有2个因素和3个水平分级，共计9组试验。因素A为耦合介质，分为水、空气、泥土3个水平；因素B为不耦合系数，分为1.2，1.4，1.6三个水平，另设置一组耦合装药结构作为对比组，各影响因素及取值见表5。选取炮孔周围岩石中一系列具有代表性的点，获取其应力峰值。

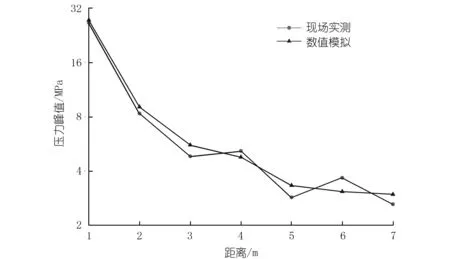
图2 不同测点压力峰值Fig.2 Peak pressure of different monitoring site

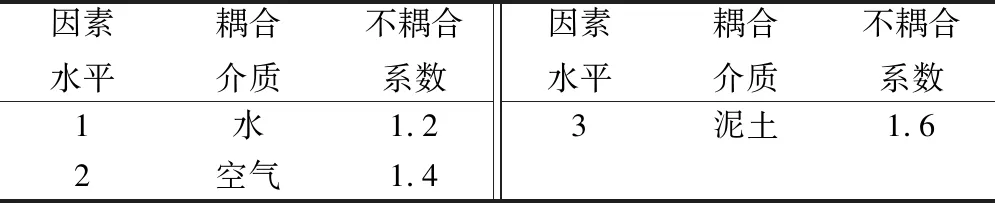
因素水平耦合介质不耦合系数因素水平耦合介质不耦合系数1水1.23泥土1.62空气1.4

3.2 正交试验结果分析

在距离药柱中心线0.5 m的岩石中分别设置3个不同位置(距水底1.5，2.9，4.3 m)的数据测点，获取其Von-Mises应力时程曲线。为节省篇幅，仅以其中任一模型计算结果为例，模型监测点布置见图3，测点的Von-Mises应力时程曲线见图4～6。

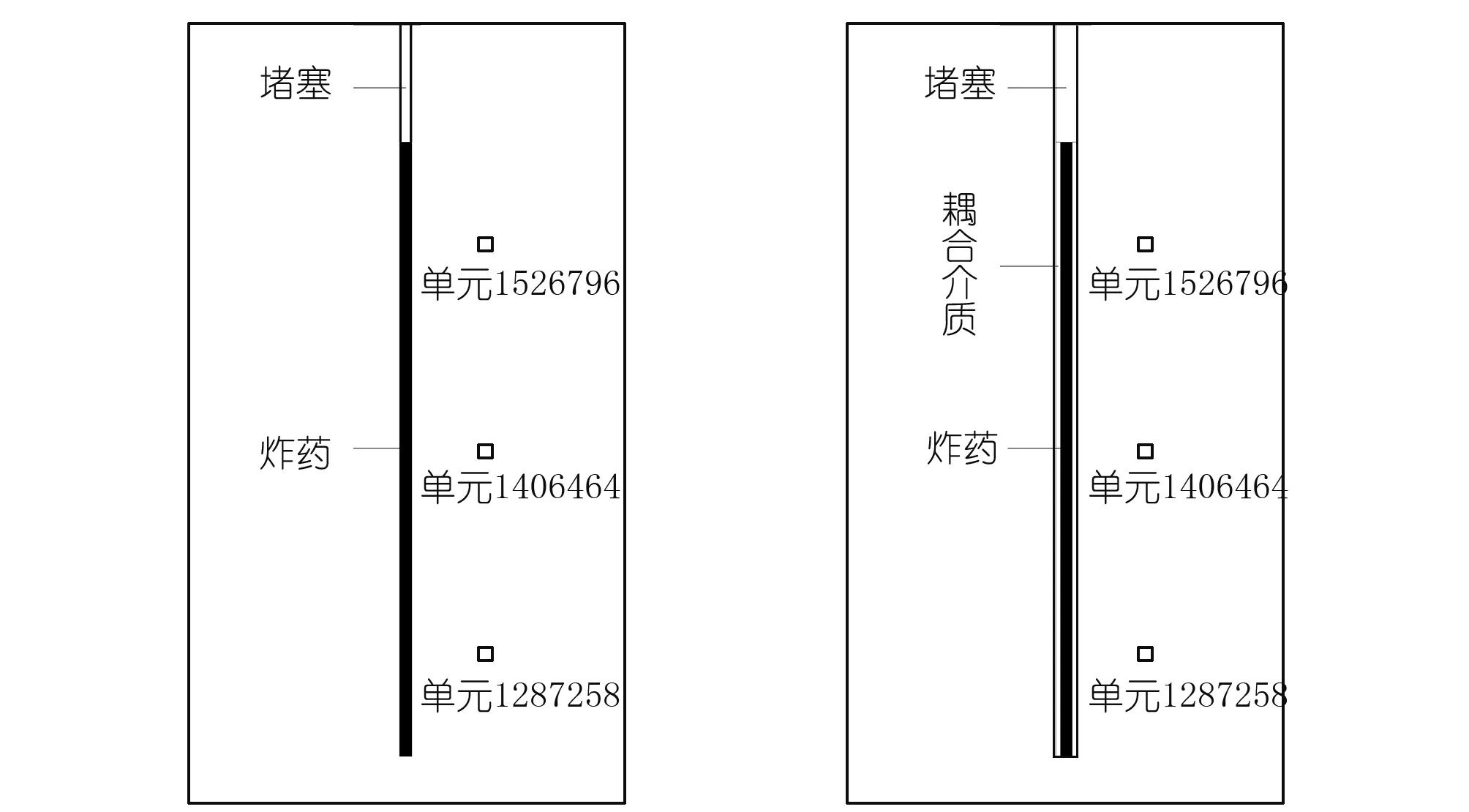
图3 模型测点Fig.3 Monitoring site of models

从测点处的应力时程曲线可以看出，应力峰值均达到了岩石的极限抗拉强度，说明都能对水中的礁石产生破坏作用。由于在水底各种波的干扰叠加较为复杂，水底单元的冲击波峰值持续时间非常短暂，仅从某一时间点的峰值应力大小来看，不足以说明荷载的作用。

图4 距水底1.5 m处测点应力时程曲线Fig.4 Von-Mises stress curve of monitoring site from the bottom of 1.5 m

图5 距水底2.9 m处测点应力时程曲线Fig.5 Von-Mises stress curve of monitoring site from the bottom of 2.9 m

图6 距水底4.3 m处测点应力时程曲线Fig.6 Von-Mises stress curve of monitoring site from the bottom of 4.3 m

因此，本文将应力时程曲线上的应力作用时间长短作为爆破效果的一个评价标准，取应力值未收敛前作用时间段为有效作用时间。对比组(耦合装药)距水底1.5 m处测点的应力作用时间为4.16 ms，试验组(耦合介质为水，不耦合系数1.2)距水底1.5 m处测点的应力作用时间为6.79 ms，作用时间延长了63.22%；对比组(耦合装药)距水底2.9 m处测点的应力作用时间为4.38 ms，试验组(耦合介质为水，不耦合系数1.2)距水底2.9 m处测点的应力作用时间为7.01 ms，作用时间延长了60.05%；对比组(耦合装药)距水底4.3 m处测点的应力作用时间为4.24 ms，试验组(耦合介质为水，不耦合系数1.2)距水底4.3 m处测点的应力作用时间为6.43 ms，作用时间延长了51.65%。取3个测点延长时间的平均值，即试验组比对比组的平均应力作用时间延长了58.31%。用相同的方法可求得其余8个试验组的平均应力作用延长时间，计算结果见表6。

从表6可以看出，设置不耦合装药结构能很大程度上提高爆炸冲击波对岩石的作用时间，作用时长相对于耦合装药结果延长了34.72%～67.42%，其中耦合介质为水、不耦合系数为1.4时，作用时间最长。耦合介质为水时，能获得较长延长时间，泥土次之，空气最小。这主要是因为水的不可压缩性、较高的密度以及较大的流动黏度，使得水中爆轰产物的膨胀速度要慢，传递给岩石的爆破能量较多，分布更加均匀、利用率高，同时延长了爆炸冲击波的作用时间。从表6中还可以看出不同耦合系数的泥土介质装药结构与水介质装药结构对作用时间的延长效果具有一定的相似性，这是因为泥土不耦合装药起爆时，其作用过程与水不耦合装药类似，泥土具有低压缩性及一定的流动黏度，受爆轰波和高温高压爆生气体产物的冲击作用，在泥土介质中激起冲击波，冲击波传播到炮孔孔壁时发生反射和透射，延长了作用时间。

表6 正交模拟试验结果Tab.6 Results of orthogonal experiment

4 现场监测及分析

根据正交数值模拟试验得出的结果，2018年7月在现场LT7炸礁区域进行了现场试验，其中一次试验采用耦合装药结构，另一次试验采用水介质耦合、不耦合系数为1.4的不耦合装药结构，布孔和装药参数见表7 。

表7 爆孔设计参数Tab.7 Parameters of the blasting hole

从现场的爆破效果来看，相同药量下的两种装药结构均达到了预期的爆破效果；从统计数据来看，采用水介质耦合、不耦合系数为1.4的不耦合装药结构爆后岩体大块率相对耦合装药结构降低67.96%，这是因为爆破形成的高压水介质能渗入岩石裂缝中，达到破碎岩石的作用，降低岩石大块率的同时扩大了粉碎区和裂隙区的范围。爆破后的现场效果如图7～8所示。

5 结 论

基于莲沱水下爆破项目，运用ANSYS/LS-DYNA数值模拟软件建立了30 m水深下的耦合和不耦合装药结构模型，并对不同设置方式下的不耦合装药结构进行了正交模拟试验分析，得到以下研究结论。

(1) 两种装药结构均能对周围岩石起到较好的破坏作用。耦合装药结构在起爆的初始时刻应力值即达到峰值，随后快速衰减，而不耦合装药结构的初始应力低于耦合装药时，但作用时间更长。

(2) 正交模拟试验结果表明，不耦合装药能显著提高爆破能量对岩石的作用时间，相对耦合装药延长了34.72%～67.42%。当耦合介质为水、不耦合系数为1.4时，作用时间最长，结合现场爆破效果来看，大块率降低了67.96%。

图7 耦合装药结构爆后效果Fig.7 Blasting effect of coupling charge structure

图8 不耦合装药结构爆后效果Fig.8 Blasting effect of decoupling charge structure

(3) 水介质不耦合装药结构能有效延长爆破作用时间，降低爆破后的岩石大块率，提高炸药能量利用率，可在类似工程项目中采用水介质耦合、结合数值模拟合理设置不耦合系数的方式，以达到降低炸药用量，提升爆破效果的作用。