轻量非对齐卷积神经网络模型探索
何 鑫,祁 欣,马海涛,赵宇海,于长永
(东北大学 计算机科学与工程学院,沈阳 110819) E-mail:1216800155@qq.com
1 引 言
CNN(卷积神经网络)模型[1]在计算机视觉领域中取得了不俗的成果,例如图像分类[2]、目标检测[3]、风格识别[4]、语义分割[5]等.就图像分类来说,该技术在提取特征方面相较于传统模型[6]需要手动提取视觉特征来说具有显著的优势.
CNN发展至今,出现了多种网络结构,如图1所示.这些结构可以被分为三大类:传统单链卷积神经网络[7-9]、多分支非对齐卷积神经网络[10,13,14,16]和使用跳跃连接的卷积神经网络[11,12,15].在CNN发展的早期阶段,普遍使用的是传统单链卷积神经网络,其网络模型深度普遍很浅且使用了大量的模型参数,这类CNN模型包括如图1中椭圆框所表示的CNN模型.图1中矩形框所表示的多分支非对齐卷积神经网络在CNN模型结构发展过程起着重要的作用,其网络模型存在有长有短的多个分支且不同分支的卷积操作是不对齐的.跳跃连接卷积神经网络不同于以往线性增加网络深度的网络模型,如图1中虚椭圆框所表示的模型,引入了跳跃连接,可以令前驱层与后继层直接连接,解决了梯度消失问题,使得CNN可以达到很深的深度.对于图1中的所有CNN模型,模型的深度与所使用的参数数量如表1所示.
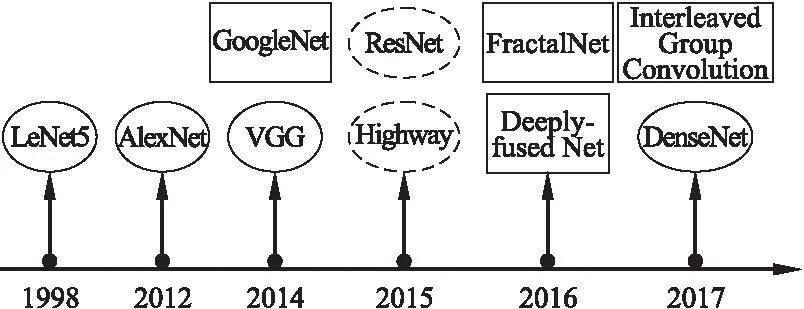
图1 CNN发展历程Fig.1 Development history of CNN
表1 各CNN模型深度及参数
Table 1 Depth and parameters of each CNN model

模型名称模型深度参数数量AlexNet860MVGG16138.36MGoogleNet226.8MResNet1101.7MDeeply-fused net503.9MFractalNet4022.9MDeseNet401.01MIGC-L32M263224.1M
对于这三种类别的CNN模型,通常使用CNN不同的层结构作为单元来描述,但除去池化层的池化操作外,其余层结构均是由神经元组成的,每个神经元是以权重W,偏置b,激活函数f(·)为单元,对神经元输入进行操作的,输入I输出O关系为O=f(WI+b),记为最小计算单元.若以最小计算单元将其标准化表示,则传统单链卷积神经网络可以视为单最小计算单元的全连接网络模型;多分支非对齐卷积神经网络可以视为分组最小计算单元间的全连接并且多组对齐结构的全连接网络模型;跳跃连接的卷积神经网络模型可以视为最小计算单元的全连接不仅仅局限在一层中,层间也存在全连接的全连接网络模型.
从卷积神经网络的发展来看,网络模型都是趋向于越来越深的模型架构.但是网络的深度越深,所带来的问题之一就是要训练的参数就越多,这就导致模型的表现会被计算资源所限制,因此削减卷积神经网络的参数冗余是必要的.目前已经有研究致力于减少卷积神经网络模型的参数冗余,如SENet[17]、ShuffleNet[18]、MobileNet[19]等.本文针对这一问题,提出了一种基于非对齐网络的CNN模型轻量化的方法.该模型是以最小计算单元作为节点,通过稀疏连接来确定数据流向,构成非对齐网络的CNN模型.本文的主要工作如下:
1)提出一种基于非对齐网络的CNN模型轻量化的方法,该模型中作为网络节点的最小计算单元可以进行组合,且以某一弃连概率值来控制生成稀疏网络的邻接矩阵,使得模型轻量化.
2)应用本文提出的基于非对齐网络的CNN模型轻量化的方法,统一地阐述最新的CNN模型,如ResNet、DenseNet、Deeply-fused Net和Interleaved Group Convolution,并通过实验来证明所提出方法的通用性.
3)实现本文提出的基于非对齐网络的CNN轻量化的方法以及DenseNet40模型,评估了模型的准确率,并对不同模型的参数数量进行了对比.实验结果表明,相较于DenseNet40,本文所提的方法以测试误差下降≤1%为代价,能够削减掉≥50%模型参数.
2 相关工作
CNN模型通常以层为单位构建网络,本文通过标准化将其表示为基于最小计算单元的模型结构,从而发现这种网络结构是以层为基础进行划分对齐.本文提出的非对齐网络结构摒弃以层为基础的模型结构,采取以最小计算单元为单位,采取以最小计算单元为网络模型的节点,每一个最小计算单元代表一个划分基准,因此非对齐网络中不存在以往CNN模型所表现出来的对齐形式.
在参数的冗余性大幅度降低的同时,还要保证模型性能没有很大的损耗,这就需要对网络中传播的有限特征进行重复使用,即特征融合.特征融合技术在最新的网络模型[12,14,15,16]中均有应用,分为两类,分别是元素层面的add操作和通道层面的concatenate操作.add的本质是增多描述图像的特征的信息量,而concatenate的本质则是融合多个描述图像的特征融合或者是融合多个输出层的信息,即增加描述图像本身的特征.本文采用concatenate操作,将不同的最小计算单元节点学到的特征进行组合连接,充分利用了模型中隐含信息并且增加了节点输入的多样性,使模型获得更多的表征能力.
3 基于非对齐网络的轻量CNN模型
3.1 uACNN模型设计
非对齐卷积神经网络(Unaligned Convolutional Neural Network,uACNN)的网络结构由两部分组成,分别是最小计算单元节点集合(记为V)以及连接两节点的边的集合(记为E),因此,uACNN可以表示为:
uACNN=(V,E)
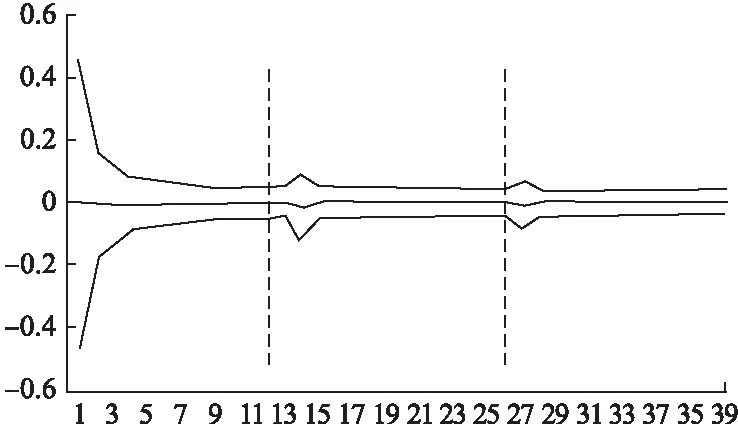
对于最小计算单元节点集合V={Vi|i=1,…,n},构成节点的Vi可以作为单独的卷积操作,也可以组合为多个卷积操作,保证了最小计算单元节点集合V所能表达卷积操作的多样性.对于连接两节点的边集合E={Eij|1 E={Eij|i∈{1·1,…,l·m}; j∈{i+1·1,…i+1·m}∪α*drop{i+2·1,…,l·m}} 生成uACNN的一般算法分为两个部分,分别是非对齐结构网络中最小计算单元节点以给定弃连概率值的配置生成算法和根据配置生成uACNN拓扑结构的算法. 算法1所得到列表中元素代表的是对应列表索引的uACNN结构中最小计算单元节点在弃连概率值α下丢弃非同一集合中的节点数目,接下来要选择uACNN结构中最小计算单元节点不连接的节点编号并且要满足所要求的约束条件. 算法1.uACNN的配置生成算法 输入:uACNN节点总数N,相同最长路径的节点个数M,弃连概率值α 输出:uACNN连接最长路径大于自身的节点数目及以弃连概率值α丢弃连接节点数目的列表P 1:i=0;p=[] 2:while i <= N-M 3: if i ==0 4: p<-(N-M)*α;i++#p中同时存入未乘α的 5: else #值,下同. 6: for j in M 7: if i%M ==0 8: p<-(N-M*int(i/M))*α+1;i++ 9: else 10: p<-(N-M*(int(i/M)+1))*α)+1;i++ 11:return p 算法2.uACNN拓扑结构生成算法 输入:uACNN节点总数N,相同最长路径节点个数M以及配置文件P 输出:uACNN节点不连接的节点编号列表Q 1:q=[] 2:for k in N-M+1 3: if k ==0 4: q <-random([M,N+1),p[k]) 5: else 6: if k%M==0 7: t1 = random([k+1,N+1),p[k]) 8: if(k+M)in t1 9: t1 <-remove(k+M);q <-t1 10: else 11: t2 = random([k+M-k%M+1,N+1),p[k]) 12: if k+M in t2 13: t2 <-remove(k+M);q <-t2 14:return q 对于上述两种算法所生成uACNN模型的拓扑结构,两节点间路径长度为1的最小计算单元的输入输出结果,执行通道层面的concatenate操作. 若uACNN中存在多个非对齐网络结构模块(unalignment block,记为uAblock),那么根据之前所述,每一个uAblock使用的弃连概率值不同,会直接影响uACNN模型的性能以及模型使用的参数数量.举个例子,假设每一个uAblock中共144个节点,分为有36组,每组有4个节点,根据3.1所介绍的uACNN模型拓扑结构生成算法,当使用三个uAblock的弃连概率值均为0的时候,使用的参数数量分别为{uAblock1:106272、uAblock2:292896、uAblock3:479520},由此可见,在性能损耗可接受的性能情况下,每个uAblock所使用的弃连概率值会直接影响uACNN模型的参数数量.对于uAblock在Cifar10数据集上分别使用概率值顺序为0.8,0.5,0.4和0.4,0.5,0.8的实验结果如表2所示. 表2 非同序弃连概率值结果 模型模型参数测试错误率uACNN8546408020.0613uACNN4584985300.0647 由表2可以看出,在性能损耗是可接受的情况下,越是靠后使用大的概率,uACNN模型使用的参数数量就是越少. 在这一小节中,将使用uACNN模型分别表示如ResNet、Deeply-fused Net、Interleaved Group Convolution等卷积神经网络模型. ResNet的网络模型结构是由残差模块构成的,每一个模块都是由多个卷积层和一个恒等映射组成.这个恒等映射将该模块的输入和输出连接到一起,然后执行add操作.因此,uACNN模型在生成最小计算单元节点集合的时候拥有与ResNet模型的残差模块中相同的过滤器个数(为了便于描述,假设残差模块的节点数为NR),即在算法1中使M等于NR,弃连概率值α设置为0,并约束节点组间的连接只存在于相邻的两组,即在算法2中所有随机生成函数使用的区间设定为[x,x+2),其中x表示同路径长度的节点数目,且执行add操作来汇总卷积结果,那么uACNN就转变为ResNet. Deeply-fused Net的网络模型与uACNN模型很相似,DFN可以看做由两个深度不同的BaseCNN组成,且两个BaseCNN在中间某些层进行融合.两个融合层之间的网络称为模块,每个模块包含来自两个BaseCNN的两个部分.若DFN的每个模块内的两个部分互换位置,可以看做两个新的BaseCNN[20].基于此,当uACNN模型在集合内部的最小计算单元节点间连接是有序的,比如集合内部存在两个节点,那么连接方式有{LL,RR,RL,LR},只需在算法1中设置弃连概率值α等于0.5;集合外部的连接是只有相邻两集合间存在,即在算法2中所有随机生成函数使用的区间设定为[x,x+2),最后通过执行add运算来汇总卷积结果.若将上述仅有单过滤器的两个不同深度BaseCNN组成的DFN模型推向更一般的DFN模型结构(如DFN(m,n),其中m和n分别代表不同深度的BaseCNN中包含的过滤器数目),可以发现其是uACNN模型结构的一种特例. Interleaved Group Convolution包括几组互补的结构化的组卷积,并且组卷积的卷积矩阵是稀疏的.故IGC模块表现出一种稀疏的形式.当约定uACNN模型在生成最小计算单元节点间连接时满足:只存在路径长度为1的两节点相连且为交叉连接,在算法1中得到的配置文件P,在传递给算法2前需要求其补集CNP,其中N为模型结构中节点总数.交替使用配置文件P和CNP来构建uACNN模型,即可表现IGC模块. 实验环境:本文所有实验的均在具有160GB RAM的Intel Xeon E5-2640服务器的单CPU核心(2.40GHz)实现,操作系统为CentOS 7.4.1708.两块NVIDIA K40 GPU用于CNN计算. Mnist数据集[21]:该数据集是包含70000张手写数字灰度图片的计算机视觉数据集,其10种数字的灰度图片是由28×28个像素点构成的.我们将数据集分为三部分:55000张图片的训练集、5000张图片的验证集和10000张图片的训练集.我们使用中心化的技术对该数据集进行预处理. Cifar-10数据集[22]:该数据集是由包含10种类别的带有32×32像素的彩色自然图像组成,其训练集和测试集分别包含50000和10000张图像.对于数据增强,我们采用广泛应用在该数据集上的标准数据增强方案(镜像/移位),对于预处理阶段,我们使用图像的均值和方差对数据进行标准化.对于每一轮模型的训练,我们使用所有的50000张训练图像,并在训练结束时报告测试错误. 4.2.1 弃连概率值对参数数量与测试错误率的影响 对为了观察uACNN模型在使用不同的弃连概率值时,网络参数使用数量以及模型测试错误率的变化,本实验设置网络模型中弃连概率值以0.1为步长,从0.1增长到0.9,实验得到uACNN网络模型对应不同弃连概率值所使用的参数数量以及测试错误率的实验结果如图2和表3所示. 表3 不同弃连概率的测试错误率(%) 0.10.20.30.40.50.60.70.80.9Cifar106.095.856.066.066.056.516.476.647.12Mnist0.310.270.290.300.310.340.310.330.38 从图2的实验结果中,我们发现弃连概率值选取得越大,uACNN网络模型所使用的参数数量就越少,总体呈下降态势;从表3的实验结果中我们发现,uACNN网络模型的测试错误率于两种数据集下均表现为在弃连概率值为0.2的时候达到最小值,在0.3,0.4,0.5和0.6,0.7时测试错误率保持相对平稳,在弃连概率值为0.9时达到最大错误率. 图2 不同弃连概率的模型参数Fig.2 Model parameters for different abandonment probabilities 4.2.2 uACNN与最新的CNN模型的对比实验 根据上一个实验的结果,本实验设计了uACNN网络模型:选取0.4,0.5,0.8的组合以对应uACNN的三个block所使用的弃连概率值.本实验中的所有的神经网络模型均使用随机梯度下降来进行训练,设置batch size为64,max epoch为150且学习率的初始值为0.1,约定在100th epoch时降低为0.01,在125th epoch时降低为0.001.权重初始化方法采用[23]所介绍的方法,并且设置权重衰减值为0.0001,Nesterov动量为0.9.实验结果如表4所示. 表4 uACNN与其他模型实验结果 模型名称模型深度/最长路径模型参数测试错误率(%)MnistCifar10ResNet11017279620.275.96IGC3824327640.265.70DenseNet4010197220.275.68uACNN(α1,2,3=0)4010522660.275.59uACNN(α1,2,3=0.4,0.5,0.8)404985300.306.47 根据表4的实验结果,可以发现uACNN的三个block在弃连概率值均设置为0的时候,与DenseNet40模型的使用参数数量以及测试错误率相差无几,这是因为当uACNN在弃连概率值设置为0的情况下,uACNN的非对齐结构将会转变为对齐结构,而uACNN的连接会两两相连,即为DenseNet的密集连接;且uACNN的数据流入每一个卷积操作组前均会进行Batch Normalization操作,故会与DenseNet40多出可忽略不计的参数,由此可见,DenseNet模型是uACNN模型的一个特例.同时可以发现,在uACNN模型所使用的参数数量相比其他CNN模型消减掉超过50%而测试错误率仅下降不到1%. 图3 Densenet40模型各层的统计值Fig.3 Statistics for each layer of the Densenet40 model 图4 uACNN模型各单元的统计值Fig.4 Statistics for each unit of the Densenet40 model 我们统计了在Cifar10数据集下uACNN(α1,2,3=0.4,0.5,0.8)和Densenet40模型各单元(层)的平均值和标准差,如图3和图4所示,我们发现两种模型在三个block中各单元(层)的参数取值走势差别不大,我们认为uACNN模型在用较少的参数即可达到接近Densenet40模型的特征表达能力,同时说明了uACNN模型有着更紧凑的特征融合.这会使得uACNN模型在使用较少的参数而准确率无大幅度的影响. CNN模型在图像识别领域中表现出良好的性能.但在实际应用中,往往会受到计算资源的限制,而减少CNN模型中卷积单元的参数冗余是解决该问题的有效手段之一.本文提出了一种基于非对齐网络的CNN模型的轻量化探索方法,能有效的减少CNN模型所使用的参数数量.实验结果表明,相比于DenseNet40模型,以测试误差下降≤1%为代价能够削减掉≥50%模型参数.如何进一步准确确定非对齐网络的连接,在减少CNN模型使用参数数量的同时减少性能的下降,是论文未来工作方向之一.
3.2 uACNN模型的优化
Table 2 Non-sequential abandonment probability result
3.3 uACNN模型的通用性
4 实验结果
4.1 实验环境与数据
4.2 实验结果与分析
Table 3 Test error rate for different abandonment probabilities
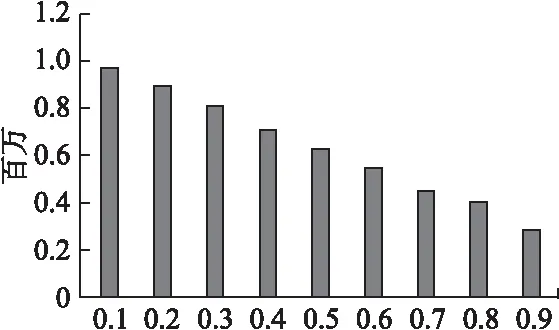
Table 4 uACNN and other model experiment results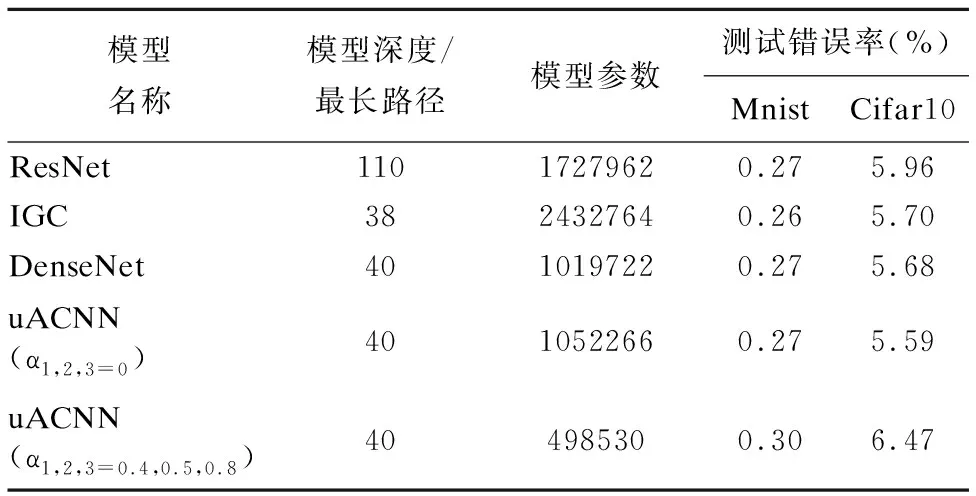

5 结 论

