套管环空压力恢复与泄压预测模型研究*
冯 定,周 宇,张 红,陈文康
(1.长江大学 机械工程学院,湖北 荆州 434023; 2.湖北省油气钻完井工具工程技术研究中心,湖北 荆州 434023; 3.非常规油气湖北省协同创新中心,湖北 武汉 430100)
0 引言
我国天然气资源丰富,但随着天然气开发工作的不断深入,气井逐渐呈现出井深、高温、高压及高产的特征,而具有上述特征的气井在生产过程中陆续出现环空带压现象[1-2]。环空带压,通常又叫持续环空压力(Sustaind Casing Pressure),是指气井环空压力在泄压后短时间内又恢复到泄压前压力水平的现象[3]。产生环空带压的主要原因包括管柱完整性失效、水泥环密封失效和地层漏失[4]。环空带压严重时会威胁管柱安全,破坏井筒完整性,甚至会导致井口装置失效,引发泄漏,造成重大安全事故[5-7]。根据环空带压发生位置的不同,可以分为油套环空带压和套管环空带压,本文主要研究了套管间环空压力的恢复和泄压过程。
目前国内外关于套管环空压力恢复的相关研究较多,主要集中在理论研究阶段,通过建立各种数学模型对环空带压的过程进行模拟预测,然后通过将生产现场的井口压力变化曲线与理论计算出的压力变化曲线匹配,从而确定井下一些无法测得的参数,如泄漏深度,泄漏孔的当量大小等,根据匹配的结果来判断现场井环空带压的严重程度[8-10]。但现有的环空带压数学模型在计算时将液柱段进行了微分,由于井口环空压力不断变化,导致液体被压缩,所以液柱段的长度在不断变化。这样就需要不断更新液柱段的微分,不仅加大了计算难度而且影响了井口环空压力值的精度。
本文主要通过研究高压气体在含微隙水泥环内的渗流规律,求解出了水泥环内气体的渗流流量。以此为基础,将水泥环上部的液柱段整体作为研究对象,并不断进行微分,然后结合气体运移过程中的质量守恒方程和井口气柱段的气体状态方程,建立了基于水泥环渗流的含液密闭套管环空压力恢复预测数学模型。该模型计算简便,考虑液柱段整体的压缩性,提高了井口环空压力值的计算精度。并且根据压力恢复时带压值的计算原理,结合泄压时的井口的嘴流公式,形成了套管环空泄压预测模型。以现场某A井为例,利用上述模型模拟计算了该井的环空压力恢复及泄压过程,并与实测结果进行曲线拟合,能够确定水泥环的渗透率,并且预测环空带压的后续发展趋势,对套管间环空带压的诊断评估和环空压力的控制具有重要意义。
1 套管环空压力恢复模型
1.1 水泥环渗流速率计算
通常情况下,水泥环的渗透率很低,气体在水泥环内的运移过程可以认为是在低渗透性多孔介质内的渗流。而水泥环边界与地层相连,地层压力近似认为不变,但水泥环上端出口压力变化,所以气体在水泥环中渗流速率随时间变化,因此水泥环内的渗流过程可以看作是气体在低渗透固体介质中的不稳定渗流[11-12]。将水泥环离散为无数个如图1所示的微元立方体,分析气体在该微元体内的流动过程。
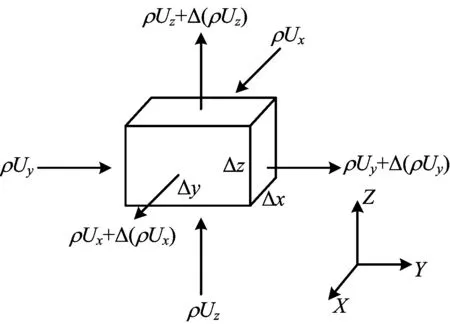
图1 气体在水泥环内的渗流微元体示意Fig.1 Schematic diagram of the micro-element of gas seepage in the cement sheath
由于气体在水泥环内主要向上运移,所以本文假设在如图1所示微元体的x和y方向上没有介质流动,所以气体在z方向上一维流动的渗流连续性方程为:
(1)
式中:ρ为气体密度,kg/m3;uz为气体在z方向上的速度,m/s;φ为介质的孔隙度。
气体在水泥环内渗流时,温度、气体黏度和压缩因子的变化都很小,可认为是等温达西渗流,所以气体渗流的运动方程为:
(2)
根据气体在水泥环内的连续性方程和运动方程,并结合气体的状态方程,通过求解,最终得关于气体在水泥环内的渗流速率:
(3)
式中:Q1为水泥环内气体渗流速率,m3/d;k为水泥环渗透率,10-3μm2;μ为气体黏度,mPa·s;Pf为产层压力,MPa;Pc为水泥环与泥浆接触面处压力,MPa;A为水泥环截面积,m2;Psc为标准状态下的气体压力,0.101 MPa;Tsc为标况下的气体温度,273.15 K;Tf为产层温度,K;L为水泥环长度,m;Z为气体偏差因子。
1.2 压力恢复时套管环空带压值计算
气井套管环空带压期间,气体的运移过程如图2所示,产层高压气体通过水泥环的微隙向上渗流,依次通过水泥环、泥浆,然后在井口聚集[13-15]。

图2 气体泄漏过程Fig.2 Gas leakage process
在模型建立过程中,忽略了气体在泥浆段的运移过程,将整个环空压力恢复周期分为若干个微元段,则在第n个时间段内井口气柱段的PVT方程为:
(4)

(5)
气体物质的量的变化量为:
(6)
(7)
式中:pt为套管环空井口压力,MPa;ng为套管环空井口气体的物质的量,mol;Vg为套管环空气柱体积,m3;Vm为套管环空液柱体积,m3;Psc为标准状态下的气体压力,0.101 Mpa;Tsc为标况下的气体温度,273.15 K;cm为泥浆压缩系数,MPa-1;R为气体常数,8.314×10-6m3·MPa/(K·mol);Z为气体偏差因子;Twh为套管环空井口温度,K;Δt为单位时长,d。
2 套管环空泄压模型
2.1 井口泄压气体速率计算
一般通过打开气井井口的针型阀泄放掉环空井口聚集的气体,假设环空泄压时针型阀处为单相气体流动,则气体流过针型阀的节流示意图如图3所示。对于压缩流体的节流过程通常分为2种状态:若流体在节流后流速达到声速,则称为临界流动;若节流后流速小于声速,则称为亚临界流动[16]。

图3 节流过程示意Fig.3 Schematic diagram of throttle process
一般通过针型阀下、上游压力之比判别针型阀处气体的流动状态[17-19]。
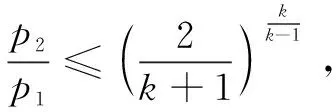
(8)
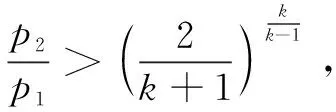
(9)
式(8)~(9)中:Q2为标况下针型阀气体流量,m3/d;p1为针型阀上游压力,MPa;p2为针型阀下游压力,MPa;dch为针型阀的开度,mm;T1为井口温度,K;γg为气体相对密度;Z为气体偏差因子;k为天然气气体绝热指数,通常取1.28。
2.2 泄压时套管环空带压值计算
泄压时套管环空带压值的计算方法和压力恢复时的一样,均以井口气柱段作为研究对象。由于泄压时针型阀处的气体排放流量远大于此时从水泥环泄漏至井口的气体流量,所以在建立泄压模型时,忽略水泥环泄漏至井口的气体。则在第n个时间段内井口气柱段的PVT方程为:
(10)
其中:
(11)
(12)
(13)
式中:pt为套管环空井口压力,MPa;ng为套管环空井口气体的物质的量,mol;Vg为套管环空气柱体积,m3;Vm为套管环空液柱体积,m3;Psc为标准状态下的气体压力,0.101 Mpa;Tsc为标况下的气体温度,273.15 K;cm为泥浆压缩系数,MPa-1;R为气体常数,8.314×10-6m3·MPa/(K·mol);Z为气体偏差因子;Twh为套管环空井口温度,K;Δt为单位时长,d。
3 现场应用
3.1 基本参数
A井完井深度为5 200 m,封隔器深度为4 500 m,储层温度134.83~143.74 ℃,储层压力76.3 MPa。该井日产气量274×104m3,套管环空井口的初始压力为0.17 MPa,温度为20 ℃。其具体的相关参数见表1。

表1 A井井身结构和流体相关参数Table 1 Related parameters of well structure and fluid for “A” well
3.2 模型验证与分析
以A井为例,根据该井的井身结构、生产数据和流体参数,利用上述的套管环空压力恢复预测模型,模拟该井的套管环空带压过程,结果如图4所示。通过计算得环空压力的计算值与实测值之间的平均相对误差不超过7%,计算结果和实测压力上升曲线基本吻合,说明了该模型具有较高的准确性。分析图4的计算结果可知,随着井口带压值的不断上升,水泥环的气体渗流流量不断减小,当渗流流量趋于0时,井口带压值趋于平稳。通过与测试数据进行拟合,预估出该井套管环空内的井口气柱约为10 mm,残留泥浆约高为2 mm,水泥环的渗透率约为100 md,为套管环空带压的诊断评估提供了理论依据。
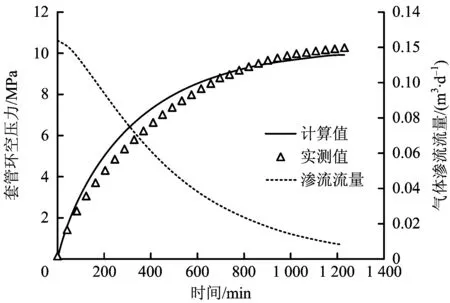
图4 A井套管环空压力恢复计算结果Fig.4 Calculation result of casing annular pressure recovery for “A” well
根据上述套管环空压力恢复的计算结果,最终该井套管环空井口的稳定带压值约为10.3 MPa,以压力恢复的计算结果作为初始条件,利用上述套管环空泄压预测模型,模拟该井的套管环空泄压过程,结果如图5所示。通过计算得环空压力的计算值与实测值之间的平均相对误差不超过21.4%,分析产生较大误差的原因为泄压过程过快导致实测数据较少,计算值与实测值之间缺乏对比。通过对泄压过程的模拟,能够有效预测泄压所需的时间,为现场环空的泄压作业提供一定的理论指导,提高了泄压过程的安全性。
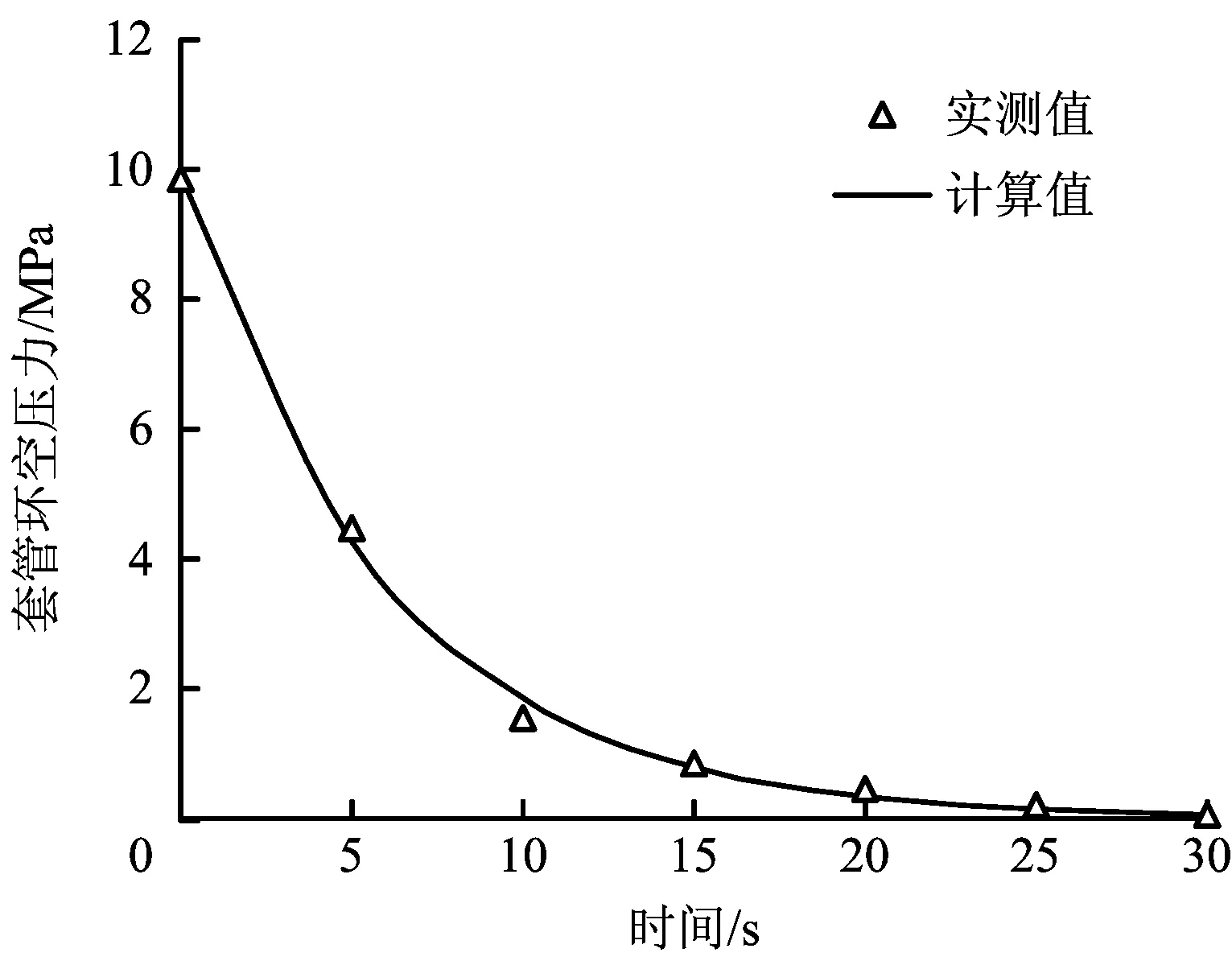
图5 A井套管环空泄压计算结果Fig.5 Calculation result of casing annular pressure relief for “A” well
4 结论
1)以套管环空水泥环内的气体为研究对象,建立了气体渗流的连续性方程和运动方程,并求解出了气体在水泥环中的渗流速率。以此为基础,考虑液柱段整体的压缩性,结合井口的气体状态方程,建立了套管环空压力恢复预测模型。
2)根据嘴流公式计算出井口泄压时针型阀处气体的流量,结合压力恢复过程中带压值的计算方法,建立了套管环空压力泄压预测模型。
3)以A井为例,根据该井的井身结构、生产数据和流体参数,结合本文的套管环空压力恢复和泄压预测模型,模拟计算了A井的压力恢复和泄压过程。结果表明:模拟计算值和现场的实测值基本吻合,模型具有较高的准确性。

