考虑土拱效应的抗滑桩桩间挡土板压力计算方法

李 婷，肖世国, 2

(1.西南交通大学地质工程系，四川 成都 610031；2.西南交通大学高速铁路线路工程教育部重点实验室，四川 成都 610031)

0 引言

悬臂式抗滑桩是一种常见的边坡支挡结构，在桩前土体开挖后，为防止桩间土体塌落，桩间通常设置混凝土挡土板。土拱效应广泛存在于抗滑桩与土体相互作用中[1]，对桩间挡土板受力影响显著。许多学者对桩间水平土拱效应进行了研究，贾海莉等[2]、周德培等[3]提出应以桩间静力平衡条件、跨中截面前缘点的强度条件和拱脚三角形受压区的截面强度条件共同控制，推导得出合理桩间距计算公式。有学者在此基础上采用考虑中间主应力的统一强度准则进行桩间距研究[4-5]。这些研究均假定土拱轴线为抛物线，且主要以平面应变问题简化分析，未考虑土拱效应沿抗滑桩深度方向变化的问题。以往曾有研究认为土拱拱体沿深度方向变化难以精确确定[6-7]。王振强[8]则通过数值模拟得出土拱矢高沿深度方向变化规律，但并未给出理论分析结果。

桩间不同深度处的土拱效应，对相应位置的桩间挡土板上的压力荷载会产生重要影响。桩间挡土板上的土压力主要由水平土拱范围内自由土体(潜在塌落土体)产生。因此，土拱拱轴线的确定对分析挡土板上土压力尤为关键。LIANG等[9]研究表明土拱轴线应是土体中最大主压应力迹线；HANDY[10]、SHUBHRA等[11]、PAIK等[12]分别提出拱型为近似悬链线、抛物线形及圆弧形拱轴线；某些现行规范[13]则设定桩间土拱为一等腰直角三角形；李邵军等[14]基于土力学和弹性力学，导出了桩间土拱的不同形态。实际上，土拱效应是反映应力偏转的一种现象，其形状并非假定的抛物线、圆弧形、等腰三角形等。另外，桩间土拱效应的产生与桩间局部土体的屈服也有密切关系，因此在分析土拱形状时还应合理引入土体的强度准则。

桩间挡土板的受力计算应以全面合理分析桩间土拱效应为前提。目前，桩间挡土板后局部坡体压力计算方法尚不完善。现行铁路规范规定[15]，桩间挡土板土压力按库仑土压力计算，但未明确如何考虑土拱效应，建议可根据桩间岩土体的稳定情况，取全部或部分土压力进行计算。叶晓明[16]、刘力生等[17]、张四平等[18]基于土拱效应，采用水平层分析法推导了一种求解桩间挡板主动土压力的方法，但均未考虑土拱矢高沿深度方向变化特征，且在同一深度处沿水平布桩方向的土压力近似按均布处理，与实际工程不符。张波等[19]、姚裕春等[20]将桩间挡土板视为简支于桩上的简支梁，这与实际三维板体的受力特征也存在差异。

有鉴于此，本文基于弹性力学解析确定桩后土体应力场及土拱形状，并充分考虑中间主应力的影响，引入Drucker-Prager强度准则[21]确定水平土拱矢高沿深度方向变化规律，进而提出桩间挡土板横向和竖向荷载分布模式，建立挡土板的三维简支板受力分析模型，并给出计算分析方法。

1 分析模型

常见抗滑桩截面形状为矩形和圆形，为方便讨论问题，本文以矩形截面抗滑桩为例进行分析。

1.1 基本假定

(1)桩后土体是均质体，水平土拱主要在桩后土体中形成。

(2)抗滑桩的桩后局部滑坡推力q为水平方向，若其与水平方向成一角度则可投影到水平方向，且滑坡推力沿深度方向呈三角形分布。

(3)桩后坡体为半无限体，相邻两桩间土体中任意点的附加应力仅受该两根桩提供的作用力影响，其他桩体影响忽略不计。

(4)土拱前侧的自由土体与拱体间的力学边界为自由边界，土拱后侧土体不传力至该自由土体，拱后土体的剩余下滑力由土拱完全传递至抗滑桩上。

1.2 基于大主应力的土拱形状

1.2.1土体中大主应力解析

根据上述假定，对于桩间距为2L，悬臂段桩长为h1，桩宽为2b的两根抗滑桩A、B，以地表以下任意深度z处的水平截面为研究对象，按平面问题考虑，建立分析模型[14]如图1所示。桩对土体的局部反作用力q=2LEz/(bh12)，其中E为设桩处桩后滑坡推力(沿桩受荷段竖向按三角形分布)。

图1 桩后土体应力场分析模型Fig.1 Analysis model for stress field of soil mass in the upslope area of stabilizing piles

根据弹性力学的Boussinesq理论[14, 21]，可推得桩后土体在桩体反力荷载q作用下，A、B两桩间任意点p的附加应力表达式。

A桩在p点的附加应力为：

(1)

B桩在p点的附加应力为：

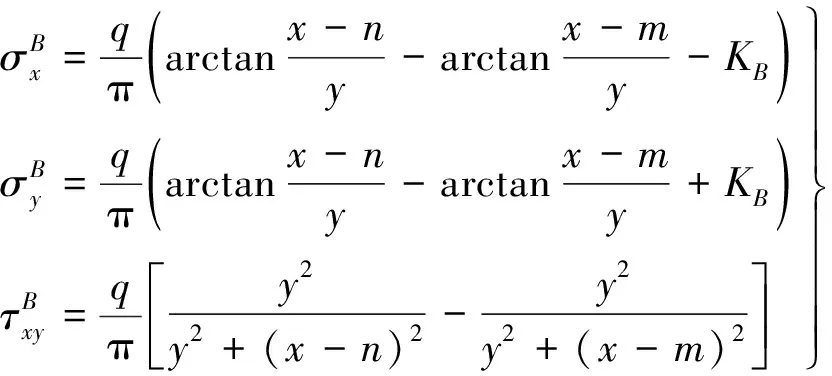
(2)

式中，

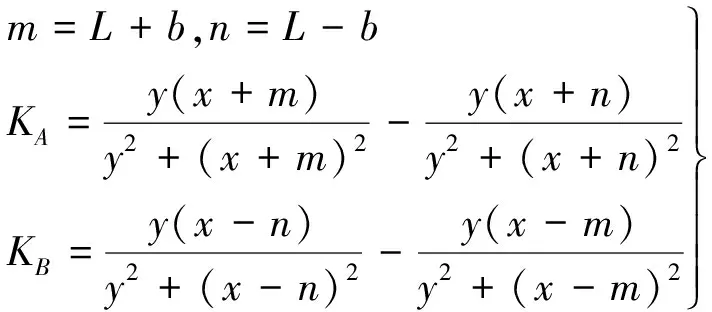
(3)

根据叠加原理，并考虑土体自重的影响，可求得桩后土体在深度z处水平截面上任一点的应力为：

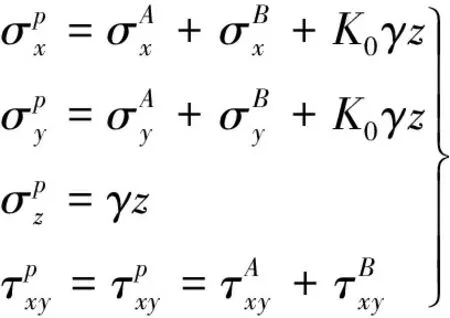
(4)

进而根据式(5)得到土体中任一点处的大主应力。

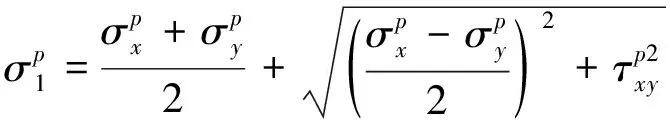
(5)

1.2.2大主应力拱形状

土拱轴线应是土体中最大主压应力迹线，因此可取桩间土体大主应力等值线的极大值点为土拱拱轴线顶点。根据式(5)，在抗滑桩间距、桩截面宽度及受荷段长度等参数已知的情况下，可以计算确定桩后土体大主应力等值线。具体可通过MTLAB电算实现，其示例结果如图2所示(L=3 m，b=1 m，h1=8 m，z=3 m，E=471.5 kN/m)。

图2 桩后土体大主应力等值线分布示例Fig.2 Contours of major principal stress of the soil in the upslope area of piles

对于该示例，桩间土体大主应力等值线的极大值分布(即土拱前缘)如图3所示。可见，土拱形状呈中间凸起而两侧略微凹陷的曲线。土拱线与x轴相交形成的不规则区域即为土拱前侧自由土体区域。该区域面积小于等腰三角形面积，这说明从工程应用角度而言，文献[13]近似采用等腰三角形是偏于安全的。

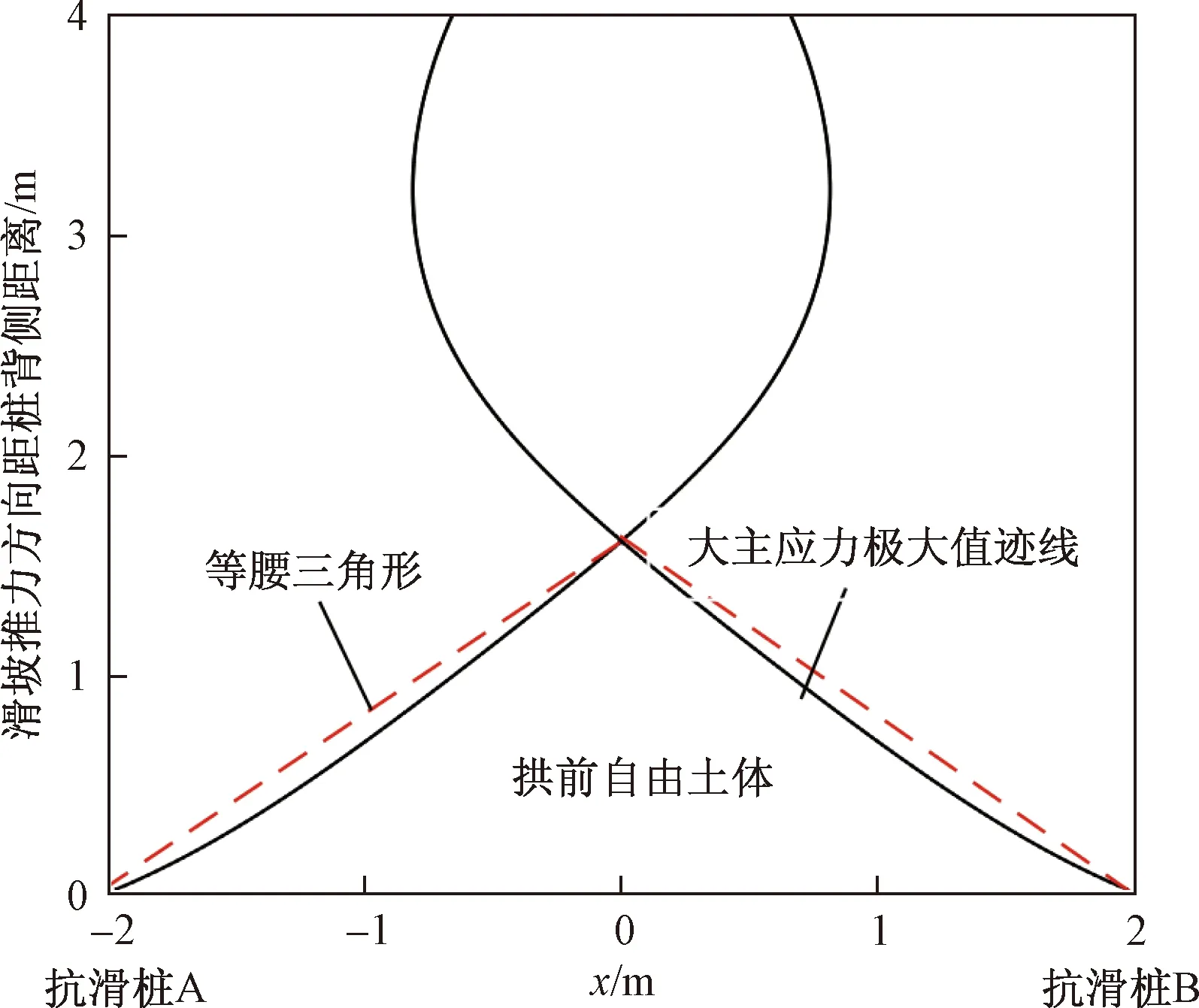
图3 桩间土体大主应力等值线的极大值分布Fig.3 Maximum major principal stress trajactory of the soil between adjacent two stabilizing piles in the example

1.3 土拱矢高沿深度变化模式

考虑到桩后土拱问题属于三维问题，这里引入含中间主应力的Drucker-Prager强度准则研究土拱效应沿深度方向变化规律。Drucker-Prager强度准则屈服函数为[21]：

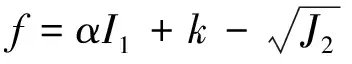
(6)

式中，I1——应力张量第一不变量；

α、k——仅与内摩擦角φ和黏聚力c有关的试验常数；

J2——应力偏量第二不变量。

由于抗滑桩桩间临空土体(挡土板施作前)在距桩顶一定深度内存在拉力区，形成竖直拉裂缝，裂缝深度z0取为：

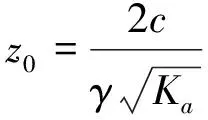
(7)

式中，Ka——主动土压力系数，Ka=tan2(45°-φ/2)。

这样，根据对称性，以抗滑桩中间位置(即矢高存在位置，x=0 m)为对象进行讨论，对于图2所示的示例，屈服函数曲线沿深度变化如图4所示。其中，桩顶到z0深度范围内为竖直拉裂缝区，在z0以下各深度处，根据式(1)～(6)可确定土体中屈服函数极大值点的位置，将这些点连接起来的迹线即可视为土拱矢高所在位置，以偏保守分析。从而得到土拱矢高沿深度方向变化规律如图5所示。可见，沿着抗滑桩深度向下，桩间水平土拱矢高先保持不变，后呈非线性减小至零，表明土拱效应在受荷段底端消失。

图4 沿深度变化的屈服函数曲线Fig.4 Yield function curve varied with depth to the pile top in the example

图5 水平土拱矢高竖向变化曲线Fig.5 Height of horizontal soil arching effect varied with depth to the pile top in the example

1.4 桩间挡土板上的荷载

桩间挡土板主要承担土拱前塌落土体自重产生的侧压力。基于前述的局部塌落拱的土拱效应分析，桩间挡土板后土压力E′可按拱前自由土体产生的静止土压力计算，即：

E′=K0W

(8)

式中：K0——静止土压力系数，K0=μ/(1-μ)，μ为泊松比；

W——拱前塌落土体的自重/kN，W=γV，其中V为拱前塌落土体的体积，γ为土体天然重度。

根据图3和图5所示结果，可将土拱平面形状简化为等腰三角形，土拱矢高沿深度则呈折线型变化。这样，沿水平布桩方向(横向)的挡土板上土压力荷载即近似为等腰三角形分布；由于折线型土拱范围内自由土体自重产生土压力是关于深度的函数，故为简化分析问题，沿抗滑桩深度方向(竖向)荷载可近似按三角形分布模式处理。于是，沿深度方向各挡土板上坡体压力q(x,z)一般分布模式如图6所示，即横向为等腰三角形、竖向为三角形分布，其表达式为：

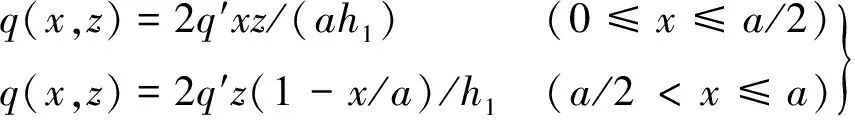
(9)

式中：a——挡土板宽度/m；

h1——各挡土板总高度(即为桩体受荷段高度)/m；

q′——最下面挡土板底边中轴线处坡体压力/ kPa。

图6 桩间挡土板上坡体压力分布模式Fig.6 Distribution mode of earth pressure on all retaining plates between adjacent two piles

根据静力平衡条件，有：

∬q(x,z)dxdz=E′

(10)

这样，对于上下布设的任一块挡土板，其上荷载可根据其竖向位置通过图6模式线性内插确定。

1.5 挡土板受力与变形计算

考虑到实际桩-板及板-板撘接方式，在按照上述方法确定出任一块挡土板上的压力荷载后，可将其视为左右两边简支(与桩撘接)、上下两边自由的简支板，从而可采用单三角级数法求解。

首先，将板体挠度函数ω(x,z)分离变量展开为：

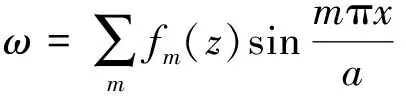
(11)

其次，将横向荷载q(x,z)展开成单三角级数：

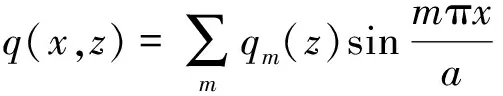
(12)

式中，

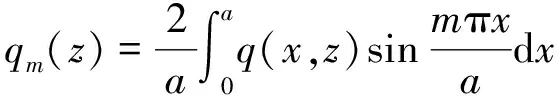
(13)

然后，将式(11)、(12)代入板体挠曲控制微分方程(14)，可得到一个常系数四阶线性常微分方程。

D▽2▽2ω=q(x,z)

(14)

式中，D为板的抗弯刚度，表达式为：

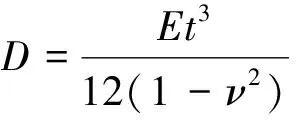
(15)

式中：E——板的弹性模量/GPa；

V——板的泊松比；

t——板的厚度/m。

最后，求解方程(14)得到挠度函数的解答式：

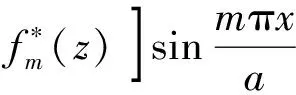
(16)

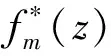
对于任一块板，自由边界条件满足：

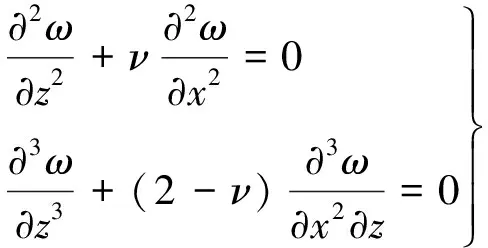
(17)

将式(16)代入式(17)中即可求得待定参数Am，Bm，Cm，Dm，进而得到挠度函数的解答。

进而将挠度函数代入式(18)～(21)可以计算得到矩形简支板的弯矩Mx、Mz和横向剪力Qx、Qz，其中下标x、z指垂直于x和z轴的平面。

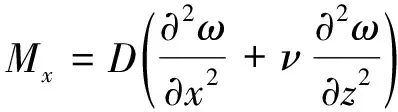
(18)

(19)

(20)

(21)

2 工程实例

2.1 土拱矢高竖向变化规律

某基岩上覆土体的开挖边坡采用悬臂式抗滑桩支挡，桩后岩土体和桩体的主要物理力学参数如表1所示。桩体材料为C30 混凝土，桩截面尺寸为2 m×3 m，桩间净距4 m，桩全长为16 m，悬臂段长度为8 m。采用前述理论分析方法和FLAC3D数值模拟分别计算桩后土拱矢高沿深度方向变化范围。数值模型如图7所示。抗滑桩采用实体单元，土体采用理想弹塑性本构模型和Mohr-Coulomb屈服准则，模型共有101 973个节点，357 707个实体单元。

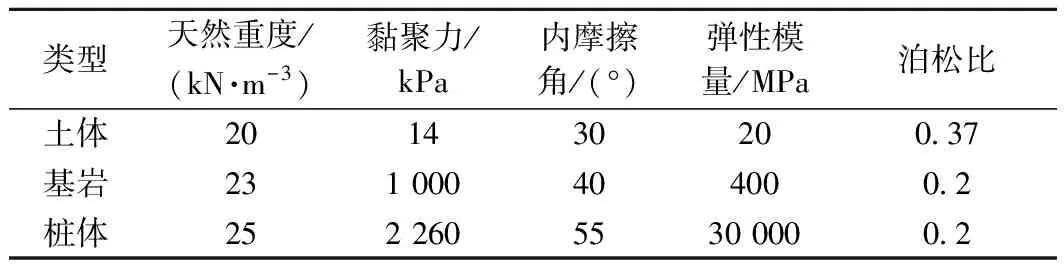
表1 实例边坡主要物理力学参数

图7 实例数值模拟计算模型Fig.7 Numerical simulation model

前述理论方法和数值模拟计算得到桩后水平土拱矢高竖向变化规律如图8所示。可见，两种方法计算结果尽管存在一定误差，但两者总体变化趋势较为吻合。沿抗滑桩深度向下，土拱拱矢逐渐减小，至受荷段底端减小至零，表明土拱效应从上至下逐渐减弱。

图8 实例水平土拱矢高沿竖向变化曲线计算结果Fig.8 Calculation results of height of horizontal soil arching effect varied with depth to the pile top in the practical example

2.2 板体内力

对于2.1节所述实例，在桩间设置混凝土挡土板支挡土体，板体材料为C20混凝土，弹性模量为25.5 GPa，泊松比为0.2，单块板高度为1 m，厚度为0.2 m。用传递系数法计算得到在设计安全系数为1.30时桩后的坡体设计推力为E=471.50 kN/m。

按前述理论方法计算得到拱前塌落土楔体体积V=23.70 m3，挡土板后侧局部土压力E′=279.66 kN，挡土板底边中轴线处压力荷载q=34.96 kPa。再将其它相关参数代入式(11)～(21)中，通过MATLAB编程计算，得到各块板体最大弯矩计算结果如表2所示。表中同时给出了规范方法[15]计算结果。可见，本文算法和规范方法计算结果相近，略小于规范方法计算结果，最大误差不超过3%。

表2 实例板体最大弯矩计算值 (kN·m)

3 结论

(1)根据弹性力学理论和应力叠加方法，推导出桩后土体任意点的大主应力表达式，可得到桩后土体的大应力等值线，通过其极大值分布图得出土拱在水面上分布形态为中间凸起而两侧略微凹陷的曲线，该曲线与两桩连线形成的区域面积小于传统近似采用的等腰三角形面积。

(2)引入Drucker-Prager强度准则考虑中间主应力对土拱效应的影响，得到土拱矢高随着深度呈非线性减小变化规律，在接近滑面处，桩间土拱效应几乎消失。

(3)通过桩间局部塌落拱的土拱效应分析，得到桩间挡土板上土压力的空间分布模式，即在同一深度处挡土板上土压力沿横向呈等腰三角形分布，沿深度方向，在全部挡土板范围内(桩受荷段范围)整体呈三角形分布。从而可按两侧桩位处简支、上下两边自由的三维板体模型分析挡土板受力与变形，给出了相应的计算公式。