信号频域变换的教学方法思考
米吉提·阿不里米提,吾米提·尤努斯,艾斯卡尔·艾木都拉
(新疆大学信息科学与工程学院,乌鲁木齐830046)
0 引言
信号处理是信息处理与通信系统专业学生重点学习内容。其中重点及难点是信号的变换域。该内容较多、概念抽象、理论性强、物理概念抽象、用到的数学工具多。信号的变换相关的基础课程包括了几乎所有的核心课程,如信号与系统、数字信号处理、语音信号处理、数字图像处理、通信原理等。信号的变换域需要讲解的最主要的内容肯定是傅立叶变换,所有专业课程肯定会讲解或应用傅立叶变换。
但是,根据个人对本科大三年纪学生(尤其是少数民族学生)的提问调查当中发现,大部分学生对概念的理解有很大缺陷。提问很简单:“傅立叶变换到底做什么?”。除了少部分学生回答:“傅立叶变换将时域信号转换成频域信号”之外,大部分学生答不出,或给出的答案是:“傅立叶变换将模拟信号变换成数字(或离散)信号”。奇怪的是,所有学生都能正确写出傅立叶变换的普遍公式。调查结果是出乎意料的。信息与通信专业的学生给出这样的答案,可以说他们对本专业是陌生的。从多个班级的学生调查当中发现,这个情况是普遍的存在的。说明学生对基本概念的理解是模糊的,多种概念严重混淆。
这个问题虽然简单,但使人联想的内容繁多,如时域信号、频域信号、连续信号、离散信号、模拟信号、数字信号、实数域、复数域等一系列专业术语,以及傅立叶变换、拉氏变换、Z 变换、卷积、乘积、相关函数等相关的概念。要在大纲规定的时间内完成教学任务,将这些概念及其内在联系教会学生,对于教师来说也是一件非常艰巨的工作。虽然在普遍公式及模拟信号的变换等方面已经有了很多形象化的教学资料[1-3],由于在实际应用当中我们用的信息一般是:有限、实数、离散信号。这些具体数据和抽象公式之间需要建立一个概念桥梁。
我们习惯的教学方法基本上是先给出抽象概念,然后进一步讲解含义和应用[1]。例如,牛顿定律、傅立叶变换等都是先给出定义,然后讲解含义。其默认的前提条件是学生已经很好地掌握了基础知识,但现实并非如此。课程及格分数限是60 分,成绩90 分以上的学生比例很少。基础不扎实会有累积效应。因此,通过简单的实用例子,可将这些内容联系到学生所学过的基础知识。一方面回顾并强化基础,另一方面能理论联系实际,提高学习热情。
随着计算机的普及,MATLAB 等数字信号处理工具软件的大量出现,一个函数调用就能实现信号的各种变换。这也会导致很多学生不关心细节,忽略基本概念的充分领会。本文以傅立叶变换为例,联系到正交变换的概念,通过实例讲解变换的具体过程。希望本文能够起到一个概念上的衔接作用。一,变换域的概念联系到学过的基础数学,二,将具体概念扩展到抽象领域中。
1 从抽象到具体
1.1 傅立叶变换的各种公式
先看看傅立叶正反变换的一般公式(1)。公式的普遍性体现在适用范围上,即复数、无限、连续信号都包括了。而且正反一对一变化。可见该公式的使用范围之广、包含的概念之丰富。
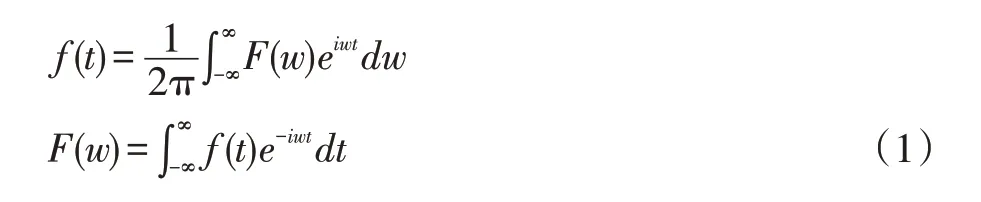
若将信号限制在有限范围内,或假设是个周期信号,则上式变成公式(2)。时域上有限的连续信号等于无限离散频域信号的累加。其反变换是在一个周期内对连续信号进行积分。式中。
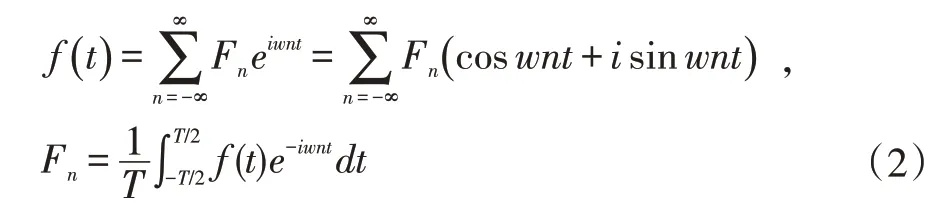
实际应用当中或计算机处理时,时间信号是离散并有限的,相应的傅立叶变换是公式(3)。离散有限时间信号对应离散有限频率信号,且等号并非近似值。为了简单易懂,我们简化了细节。

我们进一步规定信号从0 开始(时间从0 开始)的离散序列,则上式进一步简化成公式(4)。在MATLAB上的傅立叶变换函数fft()就是公式(4)的程序实现。其中是归一化系数,也可以给正反变换加同样的系数。

为了进一步简化成实数离散序列且有限信号的傅立叶变换,我们可以在公式(4)的基础上,加上一个共轭函数f-n(或偶函数镜像),变成了离散实数的傅立叶变换公式(5)[4]。图1 所示,将正轴镜像到负轴。可以看到0 点会叠加。反向推导过程是公式(10)。
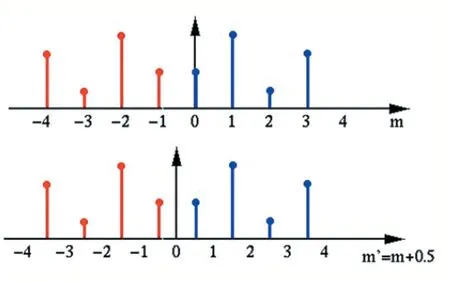
图1 正轴镜像到负轴后示意图

现在傅立叶变换变成了实数有限信号的傅立叶变换,即离散余弦变换(Discrete Cosine Transform(DCT)),公式(6)是DCT-II。在MATLAB 上的DCT 函数dct()就是公式(6)的程序实现。通过调整相位及归一化参数等可以获得各种形式,目前有DCT 变换的8 个变种。
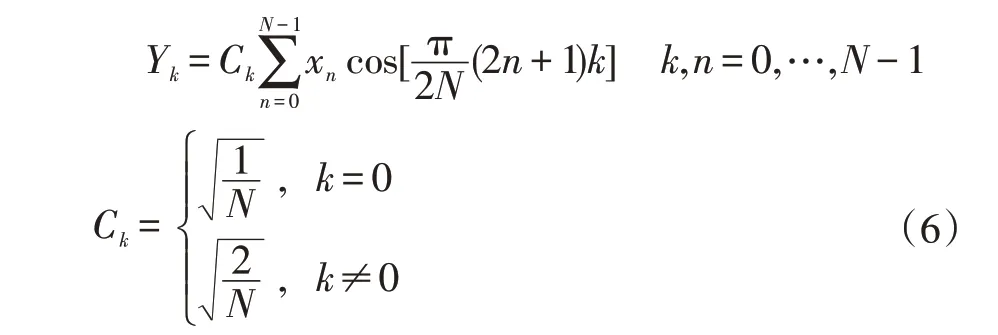
可以去掉时间及频率的概念,从一组序列(一维向量)变换成相等长度的另一组序列。正反变换一一对应,而且正反变换公式完全一样。这里给出的一维向量变换公式可以扩展成多维向量的变换公式。
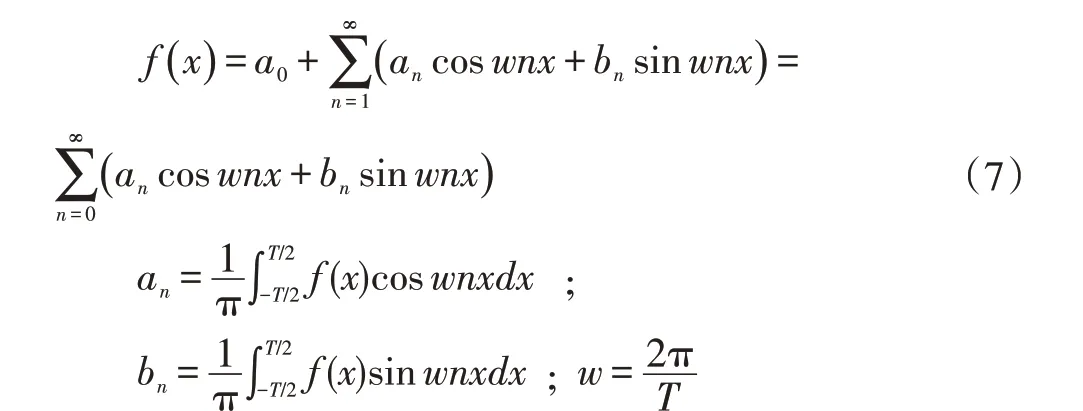
其中,f( x )是实数连续有限函数,系数an的序列代表了偶函数,系数bn的序列代表了奇函数。
我们从抽象普遍公式一路简化成实数连续及离散信号的变换公式,和学生学过的数学课程知识联系起来。可以看到公式(1-5)的一致性,这个过程是我们熟悉的教学方式,也有很多相关教学资料。但实际科学理论的发展是倒过来的,即从具体到通用抽象的理论。公式的通用性及适用范围越广,其概念越抽象。
1.2 傅立叶变换具体实例
我们举一个例子,随机取一维序列X=[ x0,x1,x2,x3]=[0.1,0.5,2,5]进行DCT 变换和傅立叶变换来解释具体计算过程。变换结果记:Y=[y0,y1,y2,y3],长度N=4。用公式(6)计算过程如下。
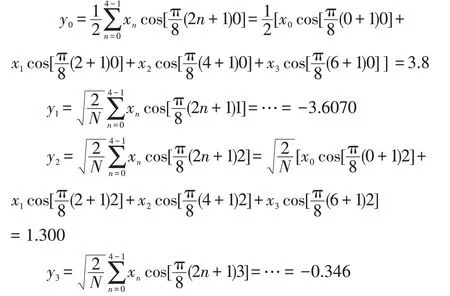
我们可以写成矩阵形式,即X 的DCT 变换是X 和变换矩阵F 的点乘。


不同的DCT 变换形式产生不同的转换矩阵和转换结果。我们再看看反变换:
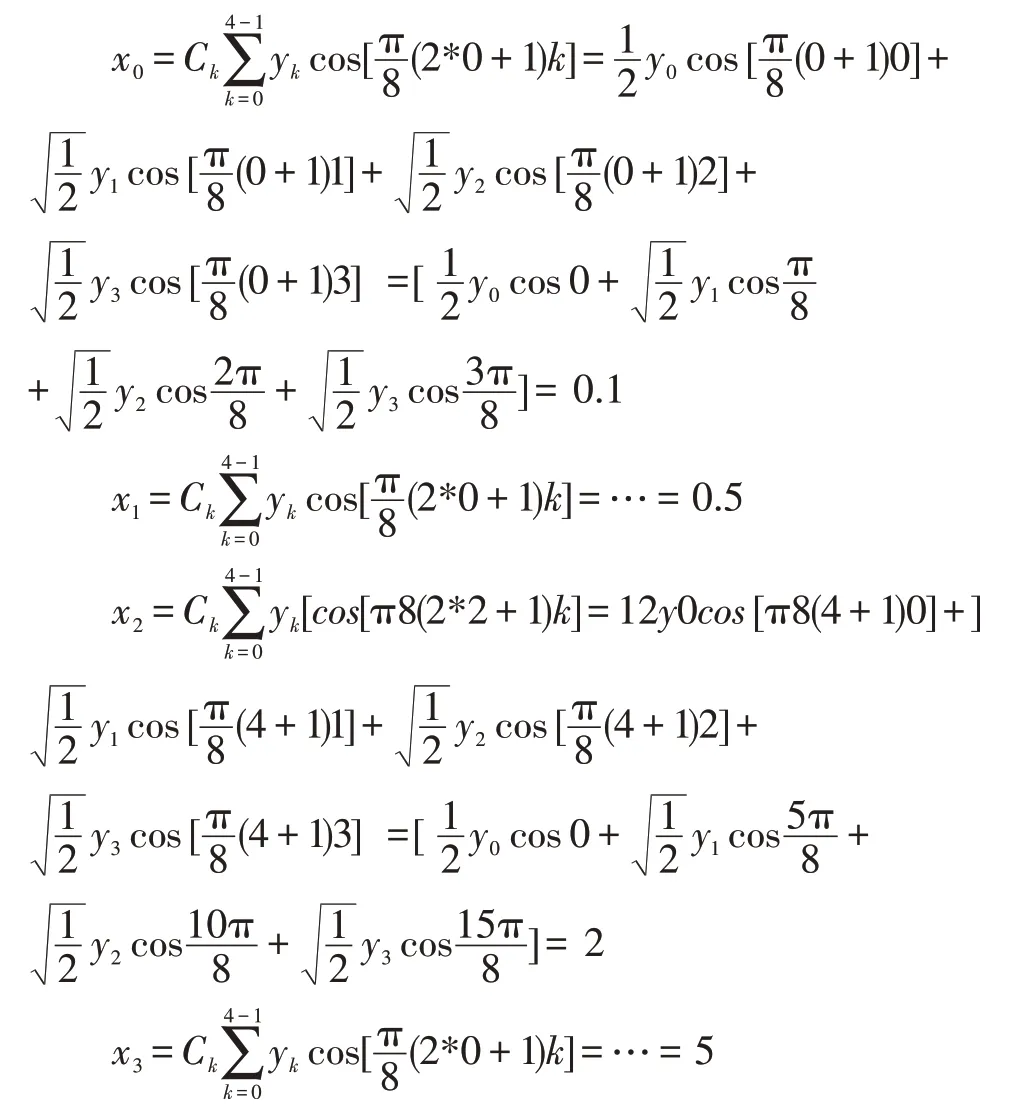
其反变换矩阵是:
反变换等于正变换的转值矩阵,而且正反变换矩阵都是正交矩阵。因为傅立叶变换属于正交变换,为了更好理解数学概念,必须对正交变换做一个简单讲解。
2 正交变换
简单的说,如果变换矩阵T 的行或列是正交的,那么变换Y=T*X 是正交变换。正交矩阵的任何两行或两列的矢量相乘等于零。若T*T*=I ,则T-1=T*,成了标准正交矩阵。1.1 小节中讨论的变换矩阵F 就满足正交性条件,所以傅立叶变化是正交变换。用计算机计算大量数据的傅立叶变换时,根据数据块维度的大小N 计算出转换矩阵就能反复使用该矩阵相乘目标数据X 就可以完成大量数据的傅立叶变换了。
下面是一个更简单的(-1 和1 构成)正交转换矩阵。这就是Walsh-Hadamard 变换,加个标准化系数就成了标准正交矩阵。
我们看看另一个正交变换公式(8),直角坐标系的坐标旋转。除此之外小波变换等很多变换方法都属于正交变换。
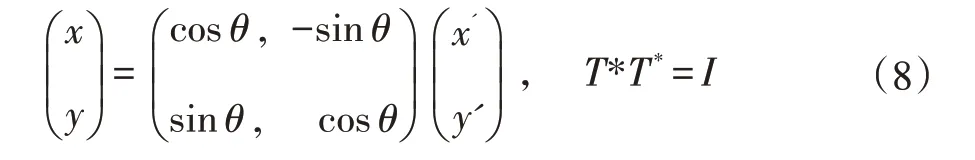
可以看到傅立叶变换是正交变换家族里面的一种变换。傅立叶变换有很多优异的性能,能量集中在某部分,每个分量代表一个频率分量,而且,离散、连续、无限、有限、实数、复数等领域都适用。电子设备甚至人和动物的耳朵结构都是类似的频率滤波器,对不同的频率分量有不同的过滤系数。
3 从具体到抽象
我们通过具体实例探讨了傅立叶变换过程及其正交特性。从正交变换可以组成一些列傅立叶变换函数。方法很简单,将单位圆周分成完全相同并对称的N 个点,从圆中心到这些点矢量夹角构成正弦和余弦正交基。
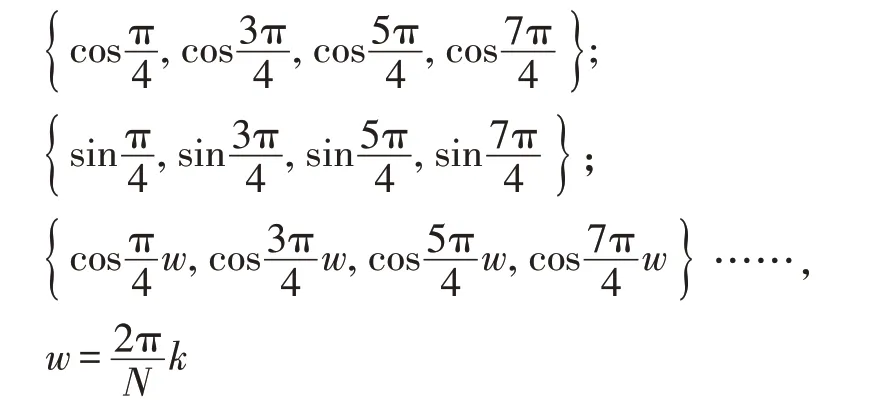
这些角度乘上周期的整数倍的w 就可以继续获得一系列正交基,即傅立叶变换矩阵。在实际应用当中通过调整初相位及归一化参数就可以获得各种傅立叶变换变种。由于正线函数是奇函数,余弦函数是偶函数,两个一起构成任何实函数。若用复平面来表示这样的关系,会更方便,且更具普遍性。直观的可以看出其概念可以推广到复数领域。当N →∞时w=导致k 趋于细分直到连续信号。我们可以看到n ↔k两者之间的关系恰好就是时间和频率的关系。图2 中底部是复平面,沿着x 轴是螺旋线,对于离散变换螺旋线也是离散的。对x 轴的采样率越高螺旋线会收紧,直到变成连续的圆柱表面。

图2 单位圆及复数傅立叶变换变化过程
从离散信号到离散信号的傅立叶变换,我们回到时间域和频率域的转换。有限的时间信号,渐渐提高采样率N →∞,直到构成一个连续的时间信号,最终有限连续时间函数对应一个无限离散序列的和,公式(7),反之亦然。
除了离散数据的傅立叶变换是正交变换外,连续信号也可以进行正交变换,对应的正交基是一系列连续正交函数。如,在一个周期内能够构成一组正交基,因为:

有了正交特性,我们才有机会计算出傅立叶级数(7)的各个系数an,bn。对等式(7)两边同时乘cos nx和sin nx 然后在一个周期内取积分就能获得每个系数。

我们将Euler 公式带入傅立叶级数(7)就可以得到复数傅立叶变换,即公式(2)。
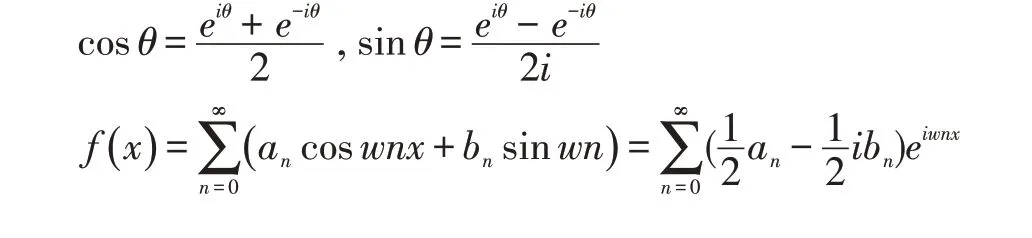

因此复数傅立叶级数是实数傅立叶变的两倍长,而且正负n 的系数是共轭的。计算一半(0,∞)就可以了。可以看到公式(10)是公式(5)的反向推导过程。
最终将复数傅立叶级数推广到连续领域就可以获得傅立叶变换一般公式(1)。因为<einx>在离散和连续领域同样满足正交性,公式(11)。
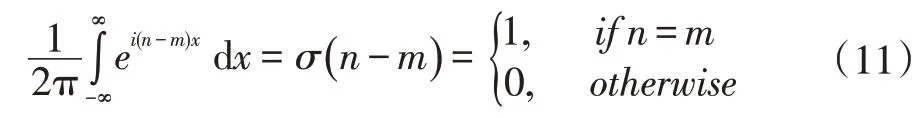
因此,有了正交性就可以将傅立叶变换推广到更大范围,并构成一个适用范围包括复数和无限领域的抽象概念。
4 结语
科学的发展过程是从具体的个例,发展成抽象的普遍规律[5]。但是抽象的概念对理解和讲解带来困难。虽然有很多解说傅立叶变换概念的文章,但是大部分是对抽象概念的讲解。用具体的案例来讲解不同适用范围,并将其联系到抽象理论的文章缺乏。因此,本文用具体的实例讲解了信号与通信专业的核心内容傅立叶变换的概念。对多种傅立叶变换及他们之间关联性进行了简单易懂的探讨。将抽象的概念和简单的基础数学联系起来讲解,为学习和实际应用提供了一个很好的参考文章。为了简便及易于理解,忽略一些细节部分。有不足之处,希望大家给予批评指正。

