基于解析几何实现Dubins 避障路径
黄金芬
(西华大学计算机与软件工程学院,成都610039)
0 引言
近年来,随着无人机的使用日益增多,以及无人机完成的任务越来越复杂,无人机的设计越来越智能,最基本的操作之一就是无人机飞行路径规划。无人机的飞行路径规划需要满足无人机飞行性能约束,以及规划出的路径最短和能躲避障碍物等需求。
目前已经有大量的路径规划方法,包括:路图法、单元分解法、概率法、势场法等。这些方法一开始是应用与地面机器人,后来人们对其进行改进和提升,应用到无人机上。这些方法的缺陷是生成的路径并不能直接运用于无人机,需要进行平滑处理得到可飞行的路径,因此,直接将曲线运用于路径规划中显得更好。基于此,Shanmugavel 等人做了大量采用曲线进行路径规划的研究,文献[1-2]描述了在二维和三维空间中规划多无人机的等长不相交Dubins 路径。文献[3]描述了在三维空间中规划多无人机的毕达哥拉斯矢端曲线(PH 曲线)路径,文献[4]描述了在二维空间中使用具有Clothoid 曲线的Dubins 路径规划多无人机的协同路径。
解析几何是常用来获取Dubins 路径的方法。本文参考了Shanmugavel 所整理的解析几何设计方法,详细介绍了根据解析几何设计二维Dubins 路径的原理和过程、检测已知静止障碍物是否和Dubins 相交的方法以及避开障碍物的方法。本文提出了原方法中没有明确给出的条件和变量的计算公式,以及根据实验结果改变了原方法中的一些公式。
1 Dubins路径
Dubins 路径可被简单地定义为,在最大曲率限制下,平面内两个有方向的点间的最短可行路径是CLC路径或CCC 路径,或是它们的子集(CL、CC、LC),其中C 表示圆弧段,L 表示与C 相切的直线段[5]。本文主要讨论CLC 路径。
1.1 初始条件和坐标计算规则
如图1 所示,点P 为起始位姿点Ps或终止位姿点Pf,θ 为对应的θs或θf,Center1 和Center2 分别为点P 右转和左转时对应圆的圆心。在给定位姿点P 下,无人机可以向左转和向右转,路径可以以顺时针方向(右)或逆时针方向(左)开始或结束,因此,一对位姿点间可以产生四条Dubins 路径,分别是LSL、LSR、RSL、RSR,其中R 表示向右转,L 表示向左转,S 表示两圆之间的切线段。

图1 相切圆
两圆之间有两条公切线:内公切线和外公切线。在指定圆的旋转方向下,同向旋转的两圆具有外公切线,反向旋转的两圆具有内公切线。图2 就属于有内公切线的反向旋转的两圆。
设计Dubins 路径时需要以下参数:
(1)起始位姿点:Ps(xs,ys,θs)。
(2)终止位姿点:Pf(xf,yf,θf)。
(3)起始曲率:ks≤kmax,其中ks=,rs是曲率半径。
(4)终点曲率:kf≤kmax,其中kf=,rf是曲率半径。
其中,下标s 表示起始位置的参数,f 表示终止位置的参数,其中θ 表示点与x 正轴的夹角。
在单位圆中,设角度基于x 正轴向左旋转为正,向右旋转为负,则在单位圆上点(x,y,θ)向左或右旋转v度后的坐标有如下计算公式:

点(x,y,θ)沿切线段前进长度v 后的坐标计算公式如下:

1.2 求解路径过程
Dubins 路径求解过程:
(1)通过下式,确定起始圆C1 圆心(xcs,ycs)和终止圆C2 圆心(xcf,ycf)。

(2)计算两圆的切点坐标。图2 是CSC 型Dubins路径中的RSL 型,其中G、F 分别是圆C1 和圆C2 上的切出点和切入点,α 是两圆圆心连线与公切线的夹角,β 是两圆圆心连线与x 轴的夹角,t 是切线段长度,c 是圆心连线的长度。
当公切线为内公切线或外公切线时,α 对应不同的计算公式。
内公切线:

外公切线:

β 对应公式如下:

β 的取值范围为(-π,π)。因此,切出点G(xG,yG)和切入点F(xF,yF)的坐标可由下式计算:

式中,θG和θF有如下公式:

其中θG0和θF0可由表1 得到。

表1 四种路径类型下切出和切入点夹角计算

图2 RSL型Dubins路径
(3)切点得到后,就可以根据以下公式得到从起始点旋转到切出点的弧所对应的角度和从切入点旋转到终止点的弧所对应的角度。
①从起始点旋转到切出点G 的弧所对应角度φs
向右旋转:
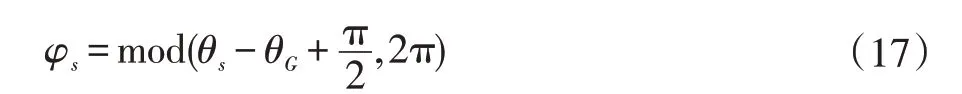
向左旋转:

②从切入点F 旋转到终止点的弧所对应角度φf向右旋转:

向左旋转:

(4)得到切线段的长度。切线段长度可以由毕达哥拉斯理论计算得到:

根据上面的步骤,求解得到了起始弧对应角度、切出点坐标、切线段长度、切入点坐标和终止弧对应角度,到此,就可以绘出Dubins 路径了。
2 避障路径
这里只讨论已知静态障碍物的避障。设计避障路径的方法有两种,一种是在规划路径时就避开障碍物,另一种是先规划出起点到终点的路径,然后对路径进行优化,使其避开障碍物。本文根据后一种方法来规划避障路径。根据前面的设计,已经得到了两位姿点间的Dubins 路径。
这里设障碍物是固定半径的圆,障碍物与Dubins路径相撞有两种情况:
(1)障碍物圆与路径中的切线段相交。
(2)障碍物圆与路径中的弧段相交。
2.1 与切线段相交
(1)与切线段相交检测方法
图3 给出了障碍物与直线段相交的几何示意图。判断是否与切线段相交,首先需要判断障碍物是否与切线段所在的直线相交,为此,要计算从障碍物中心点到直线段起始点的距离(do),同时计算障碍物中心点与该线段的垂直投影线(dn)。当直线段与障碍物相交时可以得到:

式中:ro是障碍物的半径;ko是障碍物的曲率。如果检测到障碍物与直线段相交,那么可以用余弦定理计算障碍物与直线段的交线段di:

式中的di有两个解:

这两个解可以分别写为:

当确认障碍物与直线段相交时,若dim的长度大于路径中切线段(dj)的长度,则切线段不会与障碍物相交,否则相交。图3 是障碍物与直线段相交但不与切线段相交的情形。

图3 直线与障碍物相交
(2)障碍物与切线段相交
由表1可知,无水关门工况下单缸启闭机最大推力为707.1 kN,出现在无水关门初始时;最大拉力为209.1 kN,出现在顺风无水关门终了时。
当障碍物与切线段相交时,比较简单的处理就是切线段从障碍物圆上绕过去。如图4 所示,通过调整初始运动弧和终止运动弧使切线段与障碍物圆相切,这有两种可行解:绕障碍物圆同向旋转或反向旋转。
最终的避障路径是包括两个直线段和三个弧段,在设计时,可以看做是把两个Dubins 路径合并而成。求解方法和求解单个Dubins 路径类似,这里不做介绍。

图4 直线段与障碍物相交时的避障路径
2.2 与弧段相交
(1)与弧段相交的检测方法
图5 给出了障碍物圆与弧段相交的几何示意图。相交的必要条件是弧段圆心到障碍物圆心的距离dc应满足两圆相交的条件。该条件是:

式中:rn是弧段所在圆半径,ro是障碍物圆半径。若此条件满足,还需考虑相交的交点是否落在圆弧段内,如果没有,则没有相交,否则相交。

图5 弧段与障碍物相交的情况
交点是否落在圆弧段内可以通过交点的夹角是否落于弧段对应角度范围来判断,获取弧段对应角度范围需要考虑两种情况,弧段向右旋转和向左旋转。
向右旋转时,若θt-len <0,则弧段对应的角度范围为:

否则为:


否则为:
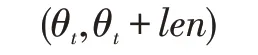
其中,θt表示弧段起点与x 正轴的夹角,len 表示弧段对应的角度大小。
(2)障碍物与弧段相交
当弧段与障碍物相交时,需要通过调整弧段的曲率来避开障碍物,图6 描述了相应的两种解,由这两种解得到的弧段均与障碍物相切,运用余弦定理可以计算此时弧段的新半径rn。即:

其中cos(μ)可以由单位向量t→[xt,yt]和n→[xn,yn]求得,即:


图6 避开与障碍物相交的2种相切圆
当圆向右转时:

当圆向左转时:


向量AB 表示由点A 指向点B 的单位向量。

图7 无障碍物路径
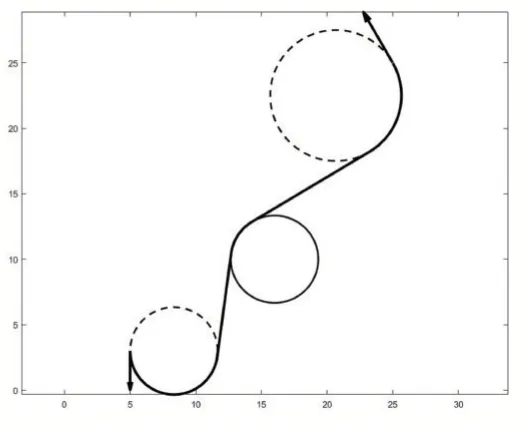
图8 切线段避障路径

图9 弧段避障路径

图10 多障碍物避障路径
3 仿真验证
设定初始条件,对本文设计的路径规划算法进行仿真验证。图7 是无障碍物环境下规划出的最短路径,图8 是障碍物与切线段相交时的避障路径,图9 是障碍物与弧段相交时的避障路径,图10 是多个障碍物存在时的避障路径。图中虚线圆是弧段所在的圆或弧段避障之前所在的圆,实线圆代表障碍物。
从图8 可以看出,切线段避障时,可以绕障碍物同向运动或者反向运动,我们选择其中更短的路径作为首选路径。
当障碍物与弧段相交后,对应有两个与障碍物相切的圆,如果选择半径较小的那个圆,那么新的切线段又可能会与障碍物相交,此时,需要再进行切线段的避障处理。图9 中我们选择了半径较大的圆。
从图10 可以看出,当障碍物圆与弧段所在的圆相交时,如果交点不在弧段内,那么障碍物对路径没有影响,不用进行避障处理。
4 结语
本文对基于解析几何设计Dubins 路径的原理和方法进行了详细描述,并在已有Dubins 路径的基础上进行避障分析设计,考虑了直线避障和弧段避障两种情况。仿真结果表明,算法能正确设计出两位姿点间的Dubins 路径,并根据已知障碍物信息优化已有路径,避开路径上的障碍物。

