具有初始弯曲的压气机转子振动特性分析

黄金平，张峥岳，黄道琼，窦 昱，王 伟

(1.液体火箭发动机技术重点实验室，陕西 西安 710100；2.北京航天动力研究所，北京 100076)

0 引言

工程实际中，由于制造、安装误差或运行中热效应等原因，会使得转轴存在一定的初始弯曲[1-4]。初始弯曲相当于在转子上附加了不平衡，破坏了转子原有的平衡状态，会对转子的振动产生复杂的影响[5-10]。一般情况下，初始弯曲会导致转子动挠度增加，轻则引起振动加剧、轴颈偏磨、轴承擦伤，重则会导致密封磨损、转静件碰摩，甚至还会诱发其他故障，对机组的健康运行造成严重的潜在危害。

具有初始弯曲的转子一般伴有质量不平衡，虽然初始弯曲和质量不平衡产生的原因不同(转子质量不平衡是指转子各横截面的质心连线与其几何中心连线存在偏差，而转子弯曲是转子各横截面的几何中心连线与旋转轴线不重合)，但二者的振动特征具有相似性[11-14]：相似的时域波形、振动频谱及轴心轨迹。要消除或降低初始弯曲对转子振动的影响，首先必须找出弯曲转子振动的规律，明确初始弯曲与不平衡振动的差异，准确判断初始弯曲故障的程度，以提出解决措施。

1 初始弯曲转子建模

初始弯曲可以通过经典的Jeffcott转子来说明。考虑如图1所示的Jeffcott转子模型，转子相对轴承中心线有一静态永久变形，其中：r0和α0为变形幅度和相位角；o为轴承中心线的中点；o′为不平衡及初始弯曲综合作用下转子的几何中心；E为不平衡力作用下转子的几何中心位置；G为转子质心；a为偏心距；ω为转子运行转速。转子几何中心运动方程[15]

(1)

其中，M，C，K为转子的广义质量、阻尼和刚度矩阵。

图1 初始弯曲转子示意图Fig.1 Schematic diagram of the initial bending rotor

2 初始弯曲转子振动分析

2.1 理论分析

根据转子动力学理论[15-16]

(1)

其中

φ=arctan[(2ξω/ωn)/(1-(ω/ωn)2)]

φb=φ-α0

式中：ωn为临界转速；ξ为相对阻尼系数；φ为不平衡响应相位角；φb为初始弯曲响应相位角。

无量纲响应

(2)

其中

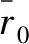
相位ψ还可以表示为

ψ=φ-Δα

(3)

其中

(4)

2.2 仿真分析

图2 振动幅值和相位随初始弯曲相位角 变化曲线 Fig.2 Curves of vibration amplitude and phase change with initial bending phase angle

取弯曲相位角α0=180°，不同弯曲因子对应的转子振动位移幅值及相位对比如图3所示。

图3 振动幅值和相位随弯曲因子的变化曲线(α0=180°) Fig.3 Curve of vibration amplitude and phase change with bending factor (α0=180°)

2.3 初始弯曲转子振动规律

通过理论和仿真分析，总结出初始弯曲转子振动具有如下特点：

2)初始弯曲的转子，其响应初始相位ψ0=-α0。而只有不平衡时，起动时刻转子响应的初始相位角为0。

4)由式(2)和式(3)可知初始弯曲不会改变转子的临界转速，但初始弯曲转子临界转速点对应的相位

只有初始弯曲相位角为0°或180°时，临界转速点对应的相位才等于90°。

5)式(2)中，对具有初始弯曲的转子B≠0，理论上A∈[0,+)，只有α0=180°时，在某一转速下转子的振幅才可能为0，此时转子出现“自平衡”，且“自平衡转速

化简获得

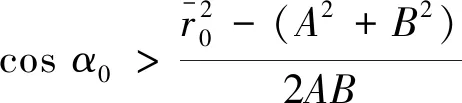
3 初始弯曲转子运行试验

第2节中获得的初始弯曲转子振动规律可用于转子的故障诊断，为初弯转子故障定位提供理论依据。以具有初始弯曲的压气机转子高速动平衡过程为例进行说明。

3.1 转子结构

某压气机转子整体结构如图4所示。转子由转轴和悬臂端叶轮两部分组成，通过螺纹连接，虽然连接部位有定位面，但由于螺纹牙之间存在间隙，安装完成后，叶轮中心线相对转轴中心线出现了一定的偏角，如图5所示。当转子装配完成后，该偏角为永久性的，这为典型的转子初始弯曲现象。

图4 转子结构示意图Fig.4 Diagram of rotor structure

图5 叶轮螺纹安装引起转子初始弯曲示意图Fig.5 Diagram of rotor bending caused by the installation of impeller threads

在进行转子运行试验前，安装完成后，沿不同轴向位置测量转轴径向跳动量，如表1所示。

表1 转子径向跳动量

3.2 试验系统简介

转子通过5叶可倾瓦轴承支承于柔性支承上，并通过膜片联轴器与驱动齿轮箱高速输出轴连接，该联轴器为轻质薄壁柔性结构，其对转子动特性的影响较小，分析中可忽略不计。P1,P2,和P3(见图4)为转子上预设的平衡校正面。3个平衡校正面处均设置有径向均布的螺纹孔，用于添加平衡校正量。采用电涡流位移传感器分别在S1，S3和S4位置(见图4)测量转子运行中的振动位移。

3.3 试验结果分析

柔性支承状态下，转子系统前3阶段临界转速分别为15 573 rpm，17 493 rpm及27 810 rpm。对应的振型如图6所示。前两阶为刚体模态，第三阶为一阶弯曲模态。

图6 压气机转子前三阶振型Fig.6 First three vibration modes of compressor rotor

转子运行过程中，S1面两正交方向振动位移信号分别记为D11和D12，S4面两正交方向振动位移信号分别记为D21和D22。

初始不平衡状态下转子升速至18 000 rpm，S1和S4两测量面处振动位移曲线如图7所示(ω1=27 810 rpm)。

初始不平衡状态下，转子在S1面处测量的振动位移随转速升高而持续增大，而S4面的振动位移峰峰值在11 124～16 686 rpm (0.4<ω/ω1<0.6)范围内出现一凹坑，且在该转速范围内相位也有所变化。参考第2节的分析，可知这种现象为转子初始弯曲，且初始弯曲主要出现在叶轮端(S4面附近)，这与转子径向跳动量测量结果(见表1)基本吻合。

通过影响系数法，在平衡面P1和P3(见图4)处对转子进行加重平衡。不同平衡状态下，转子振动位移变化曲线如图8～图10所示。

图7 初次升速转子振动位移曲线 Fig.7 Displacement curves of the rotor vibration during the initial speed up

图8 一次平衡后转子振动位移曲线Fig.8 Displacement curves of the rotor vibration after primary balancing

图9 二次平衡后转子振动位移曲线Fig.9 Displacement curves of the rotor vibration after secondary balancing

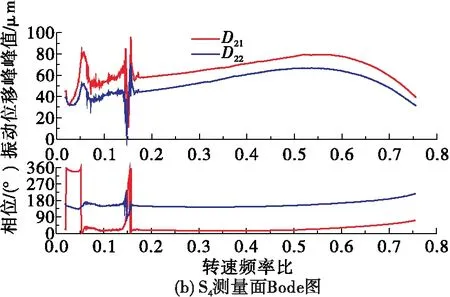
图10 平衡完成后转子振动位移曲线 Fig.10 Displacement curves of the rotor vibration after the balancing is completed

4 结论

本文通过理论分析、仿真和试验相结合的方法，研究了具有初始弯曲转子的振动特性，得出以下结论：

1)起动时刻(ω=0)，具有初始弯曲的转子其响应幅值等于初始弯曲幅度，响应初始相位与初始弯曲相位大小相等(方向相反)；而只有不平衡时，起动时刻转子的响应幅值和相位均为0。

2)初始弯曲不会改变转子的临界转速，但初始弯曲量会影响转子过临界时的振动幅值和相位，只有当初始弯曲相位角为0°或180°时，临界转速对应的振动相位才等于90°(与无初始弯曲时的相位相同)。

3)初始弯曲对刚性转子或准柔性转子振动的影响较大，而对跨临界高速运行转子(柔性转子)振动的影响相对较小。

4)具有初始弯曲的转子，经过动平衡后，在不平衡和初始弯曲共同作用下，转子在某一转速区间内响应振幅会出现一“凹坑”，且初始弯曲相位角越接近180°，“凹坑”底部对应的振幅越小。当响应幅值为0时，转子出现“自平衡”，此时初始弯曲与剩余不平衡的夹角为180°。

5)具有初始弯曲的转子，其响应幅值“凹坑”对应的转速范围随着平衡精度的提高(剩余不平衡的减小)而向高速区移动，当“凹坑”对应的转速范围落于共振转速区内时，转子的共振峰值可降至最低。

6)可通过起动时的响应(跳动量)幅值和相位、经过共振点的振动相位、平衡状态对振动幅值和相位的影响规律等综合进行转子初始弯曲的诊断和识别，并可采取合适的平衡手段，实现初始弯曲转子的平衡减振。